真空条件下钢液脱气过程的模拟研究
2022-07-12张国磊成国光代卫星姜新岩
张国磊,成国光✉,代卫星,张 旭,姜新岩
1) 北京科技大学钢铁冶金新技术国家重点实验室,北京100083 2) 西宁特殊钢股份有限公司,西宁810005
近年来,随着对高洁净钢需求的不断增加,各种真空精炼工艺对真空脱气率的要求越来越高.了解真空条件下钢液的脱气机理,对于二次精炼过程中的高效脱气是至关重要的[1-5].因此,许多冶金研究者通过采用数学模型或冷态水模型模拟了钢液脱气行为.
在数值模拟方面,基于反应位点建立的脱碳或脱气数学模型[6-10],目前得到了广泛应用.该模型假设反应主要发生在以下3个反应地点:注入的氩气气泡表面、暴露在真空环境的熔池表面以及钢液内部更加复杂的非均质形核脱气位点.对于钢液内部脱氢反应,已有文献指出,它主要发生于脱气的前期阶段,且对整个脱气过程的贡献相对较低[1,10].尽管如此,模型中关于钢液内部脱气反应位点的假设,尚未得到实验验证.
在冷态水模型中,通过测量溶解在水溶液中的O2或CO2浓度的变化来模拟研究氩气气泡表面和熔池表面的脱气反应,已有很多报道[11-18].Kitamura与Miyamoto[12]在O2气体在水中的去除实验中,通过改变熔池表面上方的气氛或在表面覆盖黏性油的方法估算熔池反应速率,并报道了熔池表面反应速率与氩气流量的0.5次方成正比;Maruoka等[13-14]采用类似的方法,在熔池表面覆盖聚乙烯颗粒替代油,测定了底吹氩气过程中的脱氧速率,阐明了熔池表面脱气反应主要发生在气泡羽流区上方“渣眼”表面,建立了熔池表面反应速率与渣眼面积的关系;Guo与Irons[15-16]通过碱性溶液中去除CO2冷态实验发现,改变负压条件比单纯增加体积流量引起的脱气效果好,并拟合了熔池表面的脱气速率公式,指出常压下脱气速率约占总体脱气的20%~40%.Kim与Yi[17]通过去除水中溶解氧模拟了RH内部反应脱气过程,认为内部反应发生在超饱和状态,然而实验过程并未排除熔池表面对脱气速率的干扰.总之,大部分冷态模拟研究过程是在常压下进行的,而对真空负压条件下的脱气速率的研究甚少.
此外,真空条件下的体积传质系数决定着整个脱气反应的难易程度,对于真空脱气精炼过程中确定合理的工艺和操作参数有着重要的指导意义.因此,本文采用饱和氧水溶液中释放溶解氧的水模型实验,通过测量不同负压下的体积传质系数(k·A·V-1),并进行回归分析,得到k·A·V-1与搅拌动能密度(ε)的函数关系.
1 实验
为研究负压条件下溶池内部的脱氧速率,设计了如图1所示水模型装置.该装置的主体部分是一个采用加厚的透明丙烯酸树脂材质制成的封闭装置,由钢包和真空室两部分嵌套而成,其中钢包的高度和内径均为0.38 m,真空室的高度和内径分别为0.40 m和0.25 m.实验涉及的主要设备包括溶氧仪(HACH,HQ40d),压力计(Infitech, PVG550),质量流量计(MF5700),真空泵,气体控制阀,螺旋桨搅拌器和数码相机等.
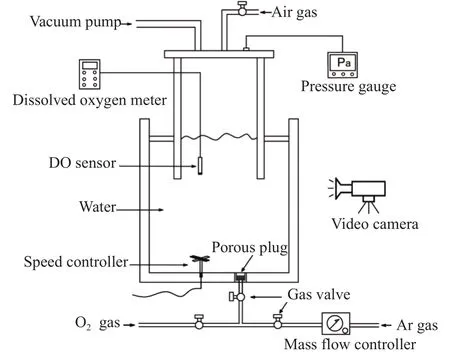
图1 实验装置示意图Fig.1 Schematic diagram of experimental apparatus
基于之前钢液脱气的数学模型[8,10],假设在真空负压条件下,氧气-水系统中溶解氧(DO)的去除反应发生在氩气气泡表面、溶池自由表面以及内部反应位点,则三个脱气反应位点的速率可由公式 (1)~(3)表示,即
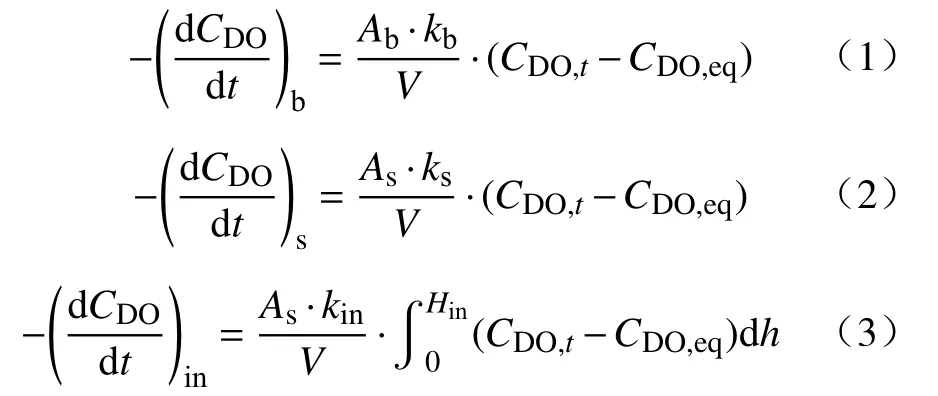
其中,A为气液界面面积,m2;k为传质系数,m·s-1;V为液态水的体积,m3;t为脱气反应时间,s;Hin为形核位点到水溶液自由表面的距离,m;CDO为水中溶解氧质量浓度,mg·L-1;下标 b、s、in 分别代表氩气气泡表面反应、溶池表面反应以及内部脱气反应,eq表示平衡状态.
在负压或搅拌实验条件下,水溶液中溶解氧的脱氧反应为

由上式可知,水中溶解氧的释放过程为表观一级反应,其脱气反应的速率表达式为
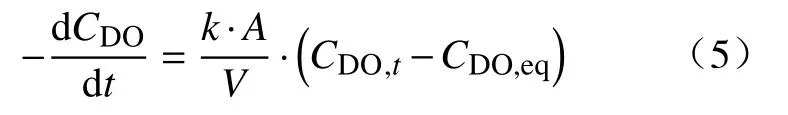
水溶液的脱气速率通常是由体积传质系数k·A·V-1来评价,可通过积分公式(5)将其表达为
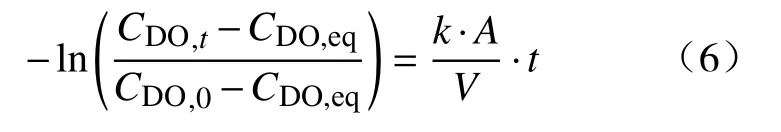
本实验通过考察真空压力、氩气流量等参数对水中溶解氧去除速率的影响展开研究.实验开始前,每组实验的水位深度均为0.38 m,向室温的水溶液中注入O2,使水中的溶解氧浓度达到预设值(9.0±0.2)mg·L-1,然后,将注入的气体转换成氩气以除去未溶解的O2分子.实验开始后,打开真空泵抽真空,调节气体控制阀控制氩气流量;在此期间,溶氧仪每隔10 s可测得并记录一次溶解氧浓度的读数,压力计可以实时记录容器内部压力的变化,数码相机可拍摄测氧探头和反应器壁面上析出的气泡,直至实验结束.
2 结果与讨论
2.1 内部脱气反应位点的存在
在纯负压无吹氩条件下,脱气反应仅可能发生在溶池自由表面和内部反应位点,此时水中DO浓度的变化情况如图2所示.图中的“虚线”表明常压下溶池自由表面的脱气速率很小,DO在常压下基本无法去除.当真空负压为15 kPa时,DO质量浓度在 240 min内可从 8.66 mg·L-1降低至6.66 mg·L-1,平均脱气速率约为 0.5 mg·L-1·h-1.此时,除了发生自由表面脱气外,很可能存在着溶池内部脱气反应.其依据为在氧-水体系中,当水溶液上方的压力低于一定值时,DO的饱和蒸气压和分压之和大于大气压、毛细管压力以及表面张力引起的静压之和时,溶解的气体分子就会析出[19],即发生内部脱气的条件为
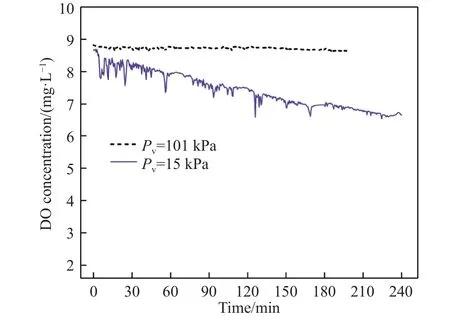
图2 负压下溶解氧随时间的变化Fig.2 Variation of dissolved oxygen concentration with time under vacuum pressure

其中,Pv、Pg分别为液态水饱和蒸汽分压和溶解氧的分压,Pa;P0为标准大气压力,Pa;ρ为液态水的密度,kg·m3;g为重力加速度,m·s-2; σ为液态水表面张力,N·m-1;r为内生气泡的临界形核半径,m.
图3观察了不同负压下溶氧仪探头表面和局部容器壁面的情况.从图中可看出,当负压为75 kPa时,在溶氧仪探头表面会观察到极少的小气泡的析出;随着压力进一步降低,虽然会在测氧探头表面开始出现较多的小气泡,但基本不发生小气泡脱离壁面的现象;当压力下降至25 kPa,在测氧探头和容器壁面开始迅速析出小气泡,随着脱气时间延长,析出的气泡开始不断长大,在600 s后,气泡已长大到一定程度,开始脱离探头表面或溶池壁面.这一现象与以往钢液脱气数学模型假设的内部反应位点的脱气过程[10,20]非常相似,即在真空条件下,熔池内部非均质形核的脱气反应发生在耐火材料表面或真空室钢液表面以下很小范围内.

图3 不同压力下溶氧仪探头表面气泡的析出过程.(a) Pv=101 kPa;(b) Pv=75 kPa; (c) Pv=50 kPa; (d) Pv=25 kPaFig.3 Bubble precipitation process from the surface of DO probe with different vacuum pressures: (a) Pv = 101 kPa; (b) Pv = 75 kPa; (c) Pv =50 kPa; (d) Pv = 25 kPa
2.2 溶池表面脱气的分离
由公式(6)可知,可通过引入机械搅拌来提高溶解氧浓度的分压Pg,使析出于壁面的小气泡快速去除.
图4为相同转速条件下不同真空压力对水中溶解氧去除效果的影响.在负压搅拌条件下,实验现象表现为:水溶液变得有雾且活跃,溶解氧小气泡一旦析出即可很快去除.图4中DO浓度的变化过程,可明显分为两个阶段:第一阶段(0~35 min),水中溶解氧浓度较高,在这种条件下,DO浓度显著下降,认为溶解氧的去除是由溶池内部脱气和自由表面脱气二者共同决定的;第二阶段(35 min以后),DO浓度下降趋势变缓,经验算该阶段的脱气速率为常数,表明此时脱气速率完全由液相传质控制.考虑到溶池表面的ks·As·V-1同样也为常数,预测这一阶段的脱气是由溶池表面脱气所贡献的.
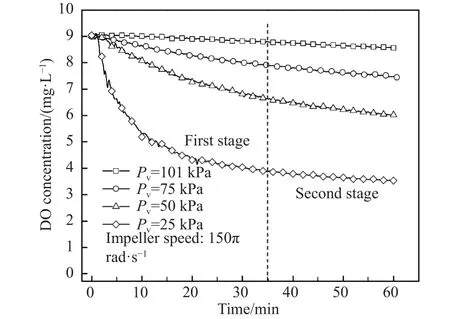
图4 相同转速下真空压力对溶解氧的影响Fig.4 Effect of vacuum pressure on dissolved oxygen concentration at a constant rotating speed
为了证实以上猜测,根据文献[12]报道,在负压吹氩气条件下,氩气气泡在水溶液表面破裂会导致的表面面积的增加,其计算公式为

其中,G为溶池自由表面非活跃的面积,m2;S为溶池表面活跃区域的横截面积,m2;α为溶池表面的活化系数;在相同搅拌能或吹氩流量条件下,G+α·S为定值.
由实验结果可得,第二阶段不同压力下测量的k·A·V-1分别为 1.66×10-3、2.418×10-3、4.305×10-3和 4.743×10-3min-1;根据理论计算,负压下的ks·As·V-1可由常压下ks·As·V-1的数值乘以压力引起的面积的变化(ΔAs)得到,其结果为 1.66×10-3、2.01×10-3、2.64×10-3和 4.17×10-3min-1,这里传质系数ks为常数[21-22].考虑到搅拌器脱气在溶池表面没有氩气泡的破裂,计算值应更小些,故在实验误差允许范围内,计算值与实验测量值吻合良好.因此,可以解释第二阶段的脱气完全由自由表面脱气引起,此时内部脱气反应基本结束.
为了描述溶池内部反应脱气的快慢程度,图5比较了两个阶段的DO的平均脱气速率,其计算公式为


图5 真空压力对溶池表面和内部脱气平均脱气速率的影响Fig.5 Effect of vacuum pressure on the average degassing rate at the bath surface and inner site
溶池内部反应的脱气速率可通过求两个阶段的脱气速率的差值获得.由图5可知,随着压力的降低,内部反应脱气的贡献率显著增加,尤其在负压25 kPa条件下,在第一阶段DO浓度处于过饱和状态,内部反应的平均脱气速率为熔池表面脱气速率的 10 倍以上;但当CDO<4.0 mg·L-1后,由于受真空负压限制,容器壁面气泡的自发析出条件(公式7)不再满足,内部脱气速率会急剧降低,这说明内部脱气反应仅发生在脱气的早期阶段或高浓度范围内.
2.3 真空脱气速率的评价
为了模拟负压下钢液的真空脱气行为,本实验中氩气流量QAr设定为1.0 L·min-1,并从面积为7.07 cm2的多孔圆形透气塞注入.图6显示了不同负压条件下DO浓度的变化规律.正如预期,降低真空压力可以显著提高脱气反应速率.同时,由负压为25 kPa对应的DO浓度变化曲线可见,在DO质量浓度降低至0.75 mg·L-1后,氧浓度很长时间内几乎没有变化,说明此时水溶液中溶解氧DO基本达到平衡浓度.

图6 真空压力对溶解氧浓度的影响Fig.6 Effect of vacuum pressure on dissolved oxygen concentration
图7给出溶解氧取对数后相对浓度与时间t的函数关系.由图可见,直线斜率表示体积传质系数k·A·V-1,DO 浓度的相对浓度与时间t呈线性关系,说明溶解氧的去除过程为一级反应,其脱气过程受液相传质控制,这与以前的研究结果基本一致[17].因此,可以利用溶解氧在水溶液中的释放模拟钢液的真空脱气过程.
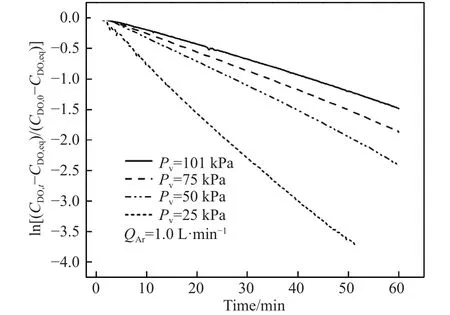
图7 真空压力下相对溶解氧浓度随时间的变化Fig.7 Variations of relative dissolved oxygen concentration with time under vacuum pressure
图8显示了不同真空和吹氩流量条件下体积传质系数k·A·V-1的实验结果.从图中可以看出,提升氩气流量或降低真空压降可以有效提高k·A·V-1,促进液相传质加速脱气反应.此外,还可以看出,在相同负压下,体积传质系数与氩气流量呈现线性相关,但对于不同真空负压条件下,k·A·V-1的值却存在着较大的差异.
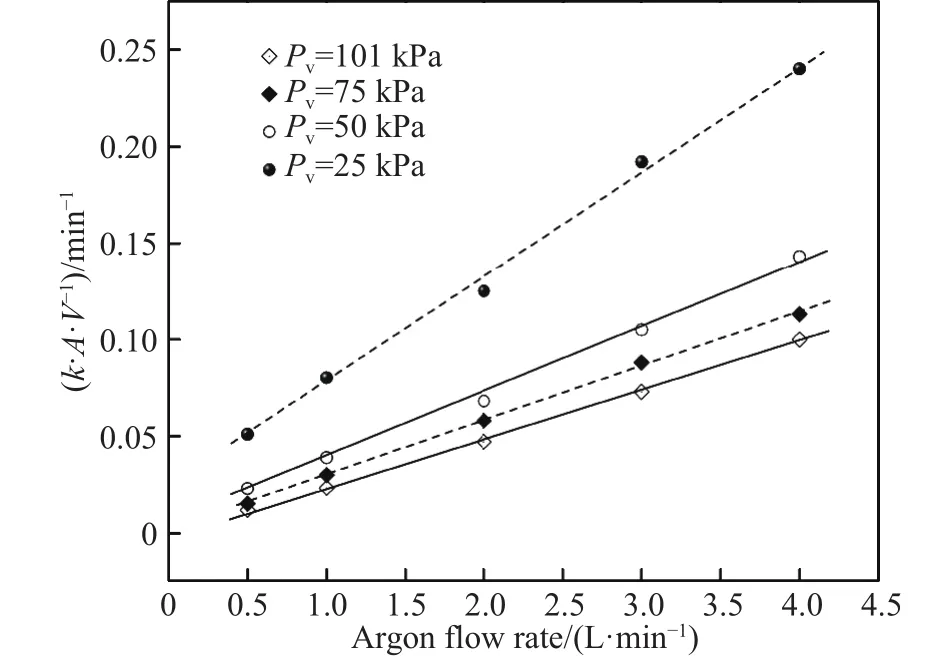
图8 不同负压下吹氩流量与体积传质系数的函数关系Fig.8 Relationship between argon flow rate and volumetric mass transfer coefficient under reduced pressure
为了定量描述负压下整体脱气速率,本文通过引入搅拌动能密度变量[23-25],探究了其对k·A·V-1的影响.在真空吹氩气条件下,氩气搅拌的动能密度ε(W·m-3)可利用全浮力模型[23]估算,即

其中,QAr为氩气流量,L·min-1;g为重力加速度,m·s-2;ρ为水的密度,kg·m3;为水位深度,m;V为液态水的体积,m3;P为容器的内部压力,Pa.
在25~101 kPa压力范围内,图9给出了实验测得的体积传质系数(k·A·V-1)与搅拌动能密度(ε)之间的函数关系,根据回归分析,得到式(11),方程的标准误差(r2)达到0.998.
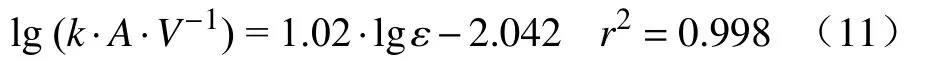
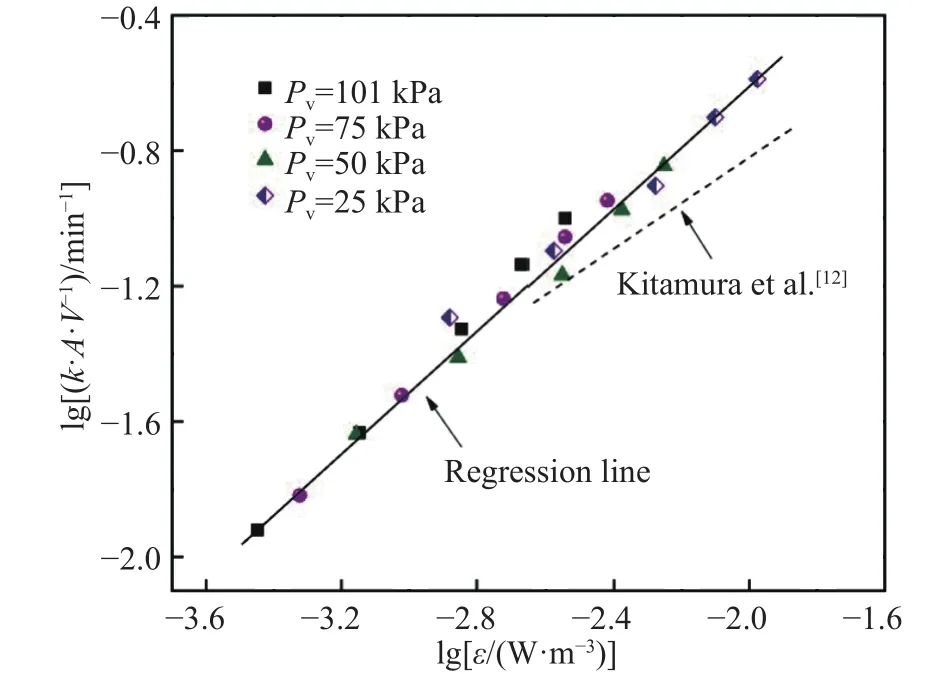
图9 搅拌动能密度对体积传质系数的影响Fig.9 Effect of stirring power density on the volumetric mass transfer coefficient
由式(11)可知,k·A·V-1与ε二者的对数之间呈现强线性相关,其中搅拌动能密度越大,k·A·V-1越大,整体脱气速率越快.该结果与Kitamura等的水模型实验结果[12]相吻合.此外,图10给出了不同学者利用数学模型对实际真空脱氢过程的预测结果[10,26].可以看到,lg (k·A·V-1)与 lgε之间同样呈强线性相关.综合分析表明,在实际真空脱气过程中,只要选择合适的真空压力、吹氩流量等参数来提高搅拌动能密度,便可提高钢液真空脱气的效率.
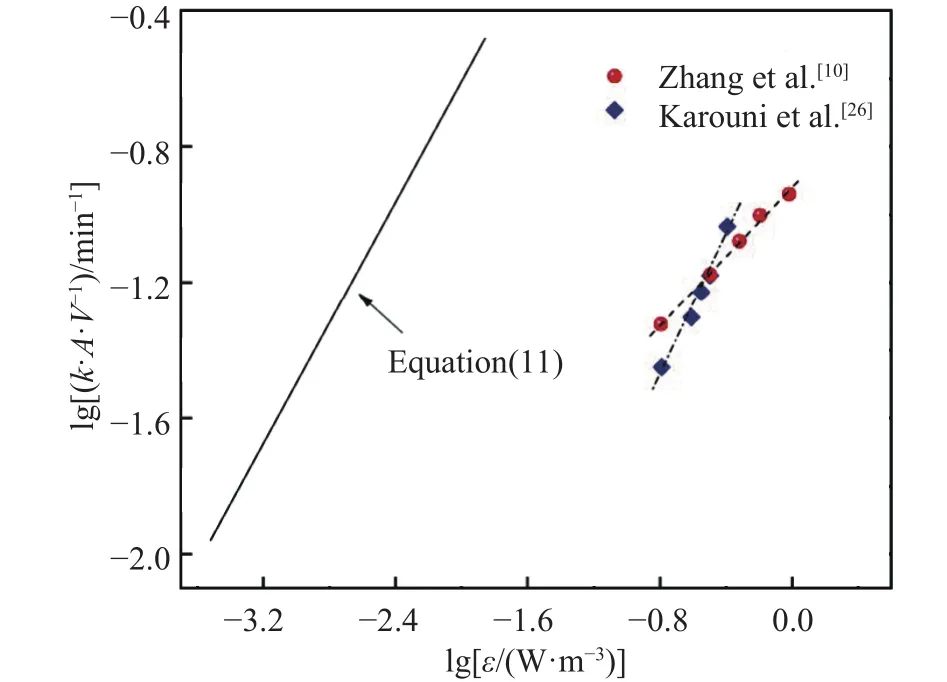
图10 真空精炼脱氢过程中数学模型预测的体积传质系数Fig.10 Prediction of volumetric mass transfer coefficient using mathematical models in vacuum refining process
3 结论
(1) 通过实验观察和理论分析,证实了以往脱气数学模型假设的内部反应位点的存在.在负压为25~75 kPa范围内,容器的壁面或其他粗糙位置会自发析出细小气泡进行内部脱气反应;当压力在25 kPa时,脱气最快,析出的气泡最多,脱气效果最佳.此外,内部脱气反应主要发生于脱气的初始阶段,即高溶解氧浓度范围内.
(2) 水模型中溶解氧浓度的对数与时间呈线性关系,其斜率k·A·V-1为体积传质系数,这与钢液真空脱气规律相类似,故可利用水模型的脱氧去除过程模拟钢液的脱气行为.为定量描述k·A·V-1,本文引入搅拌动能密度,回归得到的函数关系式为lg(k·A·V-1)=1.02·lgε-2.042,其与前人的研究结果相一致.
