隧道工程稳定可靠度研究

徐余清

（修水县交通运输局，江西修水 332400）

0 引言

进入21 世纪以来，地下空间的开发成为一个新的趋势。其中，隧道工程作为主要的地下空间工程，得到了快速的发展，其安全性和稳定性一直以来都是工程界重点关注的问题。一般采用稳定可靠度来评价隧道工程的稳定性，可靠度是指在一个规定的时间内满足预定功能的能力。20 世纪80 年代，Mataso M 与Kawamura K[1]提出在隧道工程中采用可靠度的设计方法，该方法主要是对新奥法的支护结构以概率论的原理出发，对毛洞的稳定性提出评定方法；2001 年，谭忠盛[2]经过研究，对三级围岩的直墙式衬砌结构提出在极限状态下的模糊失效概率的计算方法；2009 年，许文锋[3]提出一种模糊概率计算方法，计算海底隧道的围岩稳定性；2010 年，苏永华等人[4]在变形准则的基础上，建立隧道围岩的稳定功能函数，并将其应用于实际的公路隧道中，求解该隧道的可靠度；2012 年，李典庆等人[5]利用Monte-Carlo方法对软弱围岩的地下洞室可靠度进行计算分析。

根据目前的研究，关于隧道工程的安全稳定可靠度的研究还处于探索阶段。为此，本文对隧道工程支护结构中的锚喷支护结构的极限状态方程及稳定可靠鲁棒性进行研究，并结合实际案例进行分析。

1 隧道锚喷支护结构的分析

锚喷支护结构是利用在围岩内打入锚杆并在围岩表面喷射混凝土共同组成的支护结构，本文对围岩与锚喷支护结构的作用机理进行分析，并对该支护结构中关于围岩压力、锚喷支护的阻力及锚喷支护结构的极限状态方程进行分析研究。

1.1 围岩与锚喷支护的作用机理分析

根据相关研究表明[6-7]，围岩与锚喷支护结构的相互作用可以用特征曲线进行分析，该曲线的横坐标的数值表示隧道的洞壁径向位移，纵坐标的数值表示支护结构所受的阻力。特征曲线能够反映并描述隧道与支护结构的相关关系，分析具体的作用机理及变化趋势，对支护结构进行合理的控制。特征曲线的具体变化趋势及与支护结构的关系图形如图1所示。

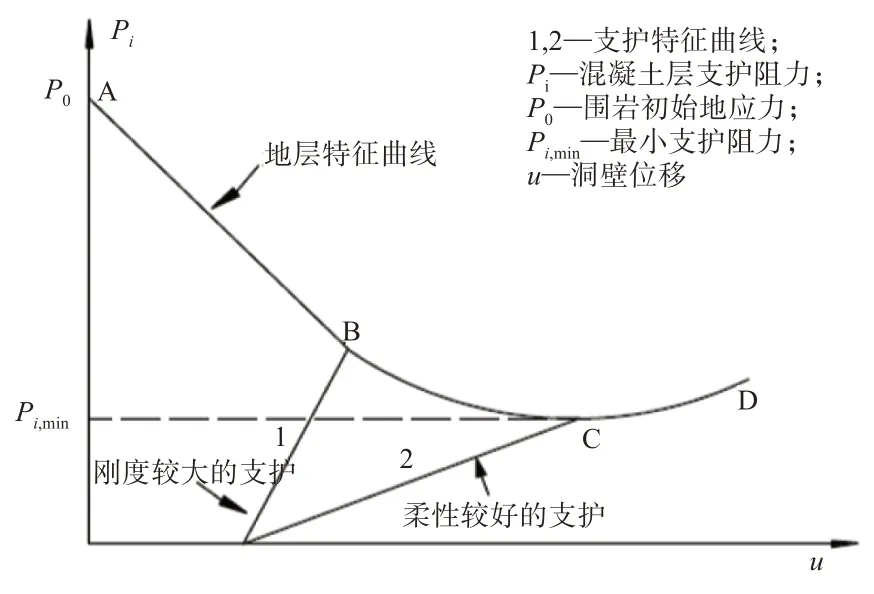
图1 隧道围岩与锚喷支护结构作用特征曲线

由图1 可知，支护结构在围岩压力作用下的变化，当隧道开挖后，在隧道自身重力作用下，应力进行重新分布，使隧道内洞壁的位移得到控制。当围岩的岩层性质较好、强度较高时，隧道内经过一定的变形，趋于新的平衡状态；当围岩的整体性较差时，为防止围岩的变形过大，应加支护结构来阻止其继续变形。如果采用刚度较大的支护结构进行支护，则出现特征曲线1 这种情况；若采用的支护结构刚度较小，则出现特征曲线2 这种情况，特征曲线1 与特征曲线2 的区别在于其支护结构能容许围岩产生的变形的多少；若支护结构本身的刚度较大，则围岩的允许变形范围将减小；若支架结构本身的刚度较小，则围岩的允许变形范围将增大。当采用刚度较小的支护结构进行隧道围岩的支护时，在C点处的围岩压力再次出现增大的现象，表明在此处进行支护较为合适。

1.2 相关计算公式

隧道工程中采用锚喷支护结构的隧道围岩产生的最小压力、锚杆支护结构产生的支护阻力、混凝土层结构产生的支护阻力等相关计算公式如下。

（1）围岩的最小压力

式（1）中：P为围岩的最小压力；c为围岩的黏聚力；φ为围岩的内摩擦角；γ为围岩的容重；r0为塑性圈的半径；P0为围岩的初始地应力。

（2）锚杆支护阻力

式（2）中：Q为锚杆的轴向拉力；S1为锚杆的纵向间距；Sc为锚杆的横向间距。

（3）混凝土层支护阻力

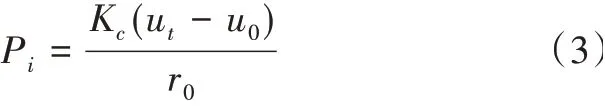
式（3）中：Kc为多喷射的混凝土的支护刚度；ut为隧道洞壁的径向位移；u0为在支护前隧道洞壁的位移；r0为隧道的半径。

（4）极限状态方程

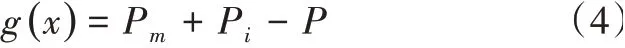
式（4）中：x为随机向量。

2 隧道工程的稳定可靠鲁棒性分析

隧道工程中的鲁棒性是指稳健性，本文基于现有的研究成果，利用隧道的稳定性相关公式建立鲁棒函数，该函数是由隧道的响应模型按不确定性因素Info-Gap的相关描述方式确定的。隧道响应模型是指R(q,u)，其中q为设计类的不确定参数，对于隧道工程采用锚喷支护结构的，其q主要是指混凝土的锚喷厚度及锚杆的支护力等，u为向量。Info-Gap理论是由非概率方法发展来的，Info是指影响结构可靠性的不确定因素，Gap是指不确定因素中已知部分和未知部位的状态关系。隧道工程中的Info-Gap的描述模型可以用式（5）表示：

式（5）中：c⇀为不确定参数的向量；t为不确定参数的第t个。

通过式（5）及隧道的响应模型可以得到稳定可靠鲁棒性公式，如式（6）所示：

式（6）表示在设计参数u的影响作用下，对某一个设计变量q，围岩中一根支护结构是否到达稳定性能的要求。

3 工程实例

3.1 工程概况

本工程中的隧道为埋深500m、直径为4m 的圆形隧道，隧道中的围岩主要是泥岩、砂泥岩及黑泥岩，从围岩的基本组成及属性判断，该隧道所处的围岩属于软弱围岩，因此在进行隧道建设时，通过研究计算分析决定采用锚喷支护结构作为隧道围岩的支护结构。该支护方案中将锚杆的约束阻力设置为200kN，实际施工中围岩的内摩擦角约为22～27°，本文计算时取25°，锚杆的间排距范围为0.95～1.05m，取间排距为1m 进行计算，开挖过程中围岩轴向的荷载最大值为140kPa[8]。软弱围岩锚喷支护后形成的类似组合拱作用形式如图2所示，其极限状态的计算公式如式（7）所示。

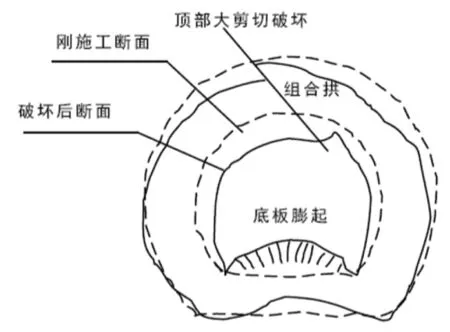
图2 组合拱形式

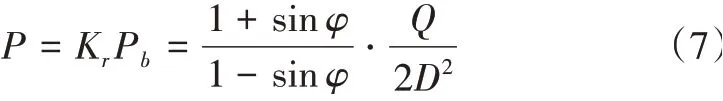
式（7）中：Kr为支护力的放大系数；φ为内摩擦角；Q为锚杆的约束阻力；D为锚杆的排间距。

3.2 计算公式

3.2.1 输出响应模型

根据本文第2节的研究，该工程的输出响应模型可以表示为式（8）。

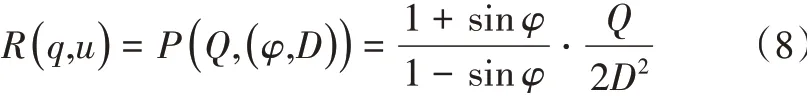
3.2.2 不确定性因素模型

根据本文3.1 章节中的方案，当内摩擦角取25°，锚杆排间距为1m 时，该工程的不确定性因素模型可表示为式（9）。

（3）鲁棒性可靠性指标

通过式（9）（10）可以得到鲁棒性的可靠性指标，如式（11）所示。

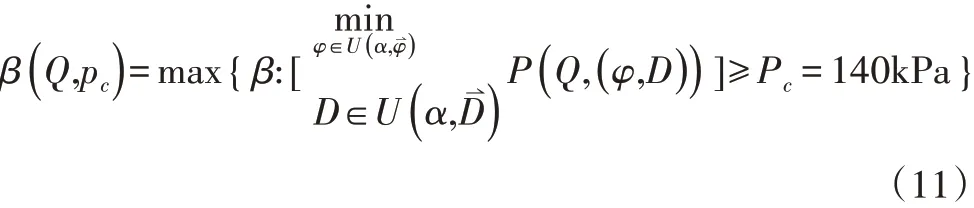
由式（11）可知，当P大于Pc时支护结构安全，隧道不会发生失稳破坏。

3.3 现场的计算结果分析

根据本工程的资料可知支承的临界应力为140kPa，而锚杆的阻力值为200kN，通过计算可得β( )

Q,pc=β(200,140) = 0.2，因此针对隧道工程中的内摩擦角及锚杆间排距两个不确定因素，其变化的范围在20%之内，即隧道围岩的内摩擦在20～29°之间，锚杆的排间距在0.8～1.2m 之间都是安全的，而从本工程的概况来看，即本隧道鲁棒性稳定可靠度满足要求，不会因隧道围岩参数及支护结构参数的改变而发生破坏。

3.4 不确定参量敏感性分析

为进一步对围岩内摩擦角和锚杆排距这两个不确定参量进行研究，本文假定三种情况分别进行分析，第一，假定排距为确定参数，围岩内摩擦角为不确定参数；第二，假定排距为不确定参数，内摩擦角为确定参数；第三，假定排距和围岩内摩擦角均为不确定参数，三种情况下均将锚杆的约束阻力按200kN进行分析。具体结果如图3所示。

图3 不确定参量影响的不确定参数曲线图

由图3可知，不论考虑一种不确定性还是考虑两种不确定性，其支承应力的变化趋势大致相同，均呈现出随不确定性参数值的增大而减小。不同的是，当仅考虑围岩内摩擦角这一项不确定性参数时，其支承应力变化的幅度最小，当不确定参数为1.0 时，对应的支承应力约为120kPa；仅考虑锚杆间排距作为不确定性参数时，其支承应力的变化幅度居中，当不确定参数为1.0 时，对应的支承应力约为78kPa，比仅考虑内摩擦角这一项不确定性时小42kPa，表明仅考虑一个参数时，锚杆间的排距对隧道的影响更大。当同时考虑围岩内摩擦角和锚杆间距的作为不确定参数时，其支承应力的变化幅度最大，当不确定性参数均为1.0 时，对应的支承应力约为25kPa，该值均比仅考虑不确定参数时的值小，由此也表明，隧道对多个不确定参量的变化反应显得更为敏感。因此，在实际的工程中应同时考虑不同因素的影响，以确保隧道的稳定安全[9]。

4 结语

本文根据现有的研究成果，对隧道工程支护结构中的锚喷支护结构的极限状态方程及稳定可靠鲁棒性进行研究，给出关于隧道工程中采用锚喷支护结构进行支护的围岩最小压力、支护阻力及锚喷支护结构的极限状态方程的相关计算公式；结合隧道施工实际案例，经过分析研究和计算，表明案例工程的鲁棒性稳定可靠度计算合理，隧道不会因隧道围岩参数及支护结构参数的改变而发生破坏。