基于上游正序参数比较的电压暂降源定位方法

孟庆伟，高 涵，贾志恒，钟振芳，何家宇

（1. 中国石油大学（华东）新能源学院，山东省 青岛市 266580；2. 国网山东省电力公司潍坊供电公司，山东省 潍坊市 261000）

0 引言

电压暂降是指电网在工频下电压有效值瞬时减小到额定值的10%～90%范围内，持续时间为半个工频周期到数秒的现象。电压暂降作为目前电力系统中最重要的电能质量问题之一，占所有电能质量问题的80%左右［1］。据统计，电压暂降不仅发生频繁，带来的影响也不容忽视，主要体现在对电网公司和用电企业的影响［2-3］。电压暂降造成的损失重大，且由电压暂降引发的客户投诉以及经济纠纷增多［4-5］。因此，为界定电压暂降事故中供用电双方各自的责任，有针对性地开展电压暂降治理，降低用电企业损失，迫切需要开展电压暂降源的上下游定位研究。

一直以来，电压暂降源的上下游定位方法都是国内外研究的热点。文献［2］提出了基于扰动能量和扰动功率的定位方法，但是该方法把电压暂降视作从系统吸收能量的过程，对受雷击的系统、含有储能元件的系统来说，适用性不佳。文献［6-8］对文献［2］提出的方法做了一定的改进，其中，文献［6］通过改进线性负载模型，利用瞬时扰动功率或其半周期平均值的极性来定位电压暂降源；文献［7］利用故障分量法重新定义了扰动功率，提高了定位的准确性。除基于扰动能量和扰动功率的方法以外，文献［8］提出了一种基于系统轨迹斜率的定位方法，该方法通过判断斜率cosθ（θ为电压和电流之间的相位角）的符号来判断电压暂降源的位置。文献［9］提出一种基于距离保护的电压暂降定位方法，即利用扰动前后阻抗角相位的变化来判断上下游。上述方法均未考虑负荷模型的影响，定位准确度受到一定的限制。

为了提高电压暂降源上下游定位的准确度，文献［10-11］对电压暂降准确识别进行了研究。文献［10］提出了一种基于深度置信网络的电压暂降特征提取与电压暂降源辨识方法，文献［11］提出了一种基于优化极限学习机的电压暂降源识别方法。文献［12］提出了基于等效阻抗实部极性的定位方法，并考虑了暂态过程中变频驱动电动机的特性，在原有判据的基础上增加了有功变化量的指标，从侧面说明了负荷对定位准确度的影响。文献［13］也考虑了含源负载的情况，将下游负载等效成电流源和等效电阻的并联，提高了定位的准确性。此外，许多定位方法从数据处理的角度在原有方法的基础上进行了改进，如利用半监督学习、神经网络、直觉模糊集等［14-16］，一定程度上提高了电压暂降源定位的准确度，但是并不能从根本上消除负荷模型对定位准确度的影响。

综上所述，目前传统电压暂降源上下游定位方法存在的主要问题是负荷模型的适用性不佳，对于不同种类的负荷，定位的准确度不同。为此，本文提出了一种无须考虑负荷模型的基于上游正序参数比较的电压暂降源定位方法。该方法首先通过戴维南等效模型获得监测点处系统的等效参数；然后，通过比较电压暂降前后上游正序参数的变化，定义参数变化指标，实现对电压暂降源的上下游定位；最后，考虑了包含参数不确定性、测量误差、计算误差在内的综合误差对定位结果的影响，引入概率型判据对引起电压暂降的上下游双方责任进行划分，提高了定位的合理性和准确性。在IEEE 标准模型中对所提方法的正确性进行了验证。

1 上游正序参数的辨识

电压暂降源的上下游定位，即是确定引起电压暂降的扰动源位于监测装置的哪一侧。如图1 所示，M为监测点，以电流流经的方向为准，箭头所指方向发生电压暂降即为系统上游，反之为系统下游。

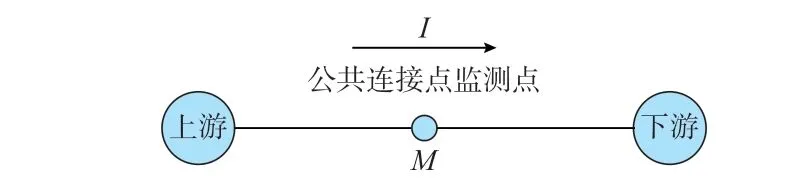
图1 电力系统上下游关系Fig.1 Relationship between upstream and downstream in power system

电力系统在监测点M处可等效为如图2 所示的戴维南等值模型。图2 中：为系统电源；Rs、RL分别为系统电阻和负载电阻；Xs、XL分别为系统电抗和负载电抗；Zs、ZL分别为系统阻抗和负载阻抗；V˙、分别为M处测得的电压和电流值，且电流I的方向是从电源侧流向用户侧，即从上游流向下游。

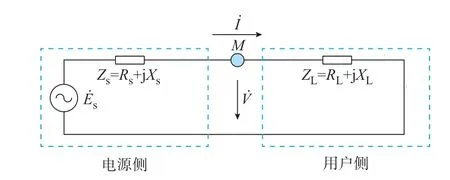
图2 电力系统戴维南等值模型Fig.2 Thevenin equivalent model of power system

由图2 可列出第i个周期上游电压平衡方程为：

式中：i=1，2，…，n，其中n为周期总数。

文献［17］中提到：在参数辨识过程中，如果选取的电压、电流的周期值过于接近或过于远离电压暂降时间段，会导致定位结果不精确。因此，需要选择多组周期数据，以提高参数辨识的准确度。所以，此处要求n≥3，即至少采集3 个时刻的电压、电流值。

将式（1）中的电压和电流相量用实部和虚部表示，可以得到如下公式：

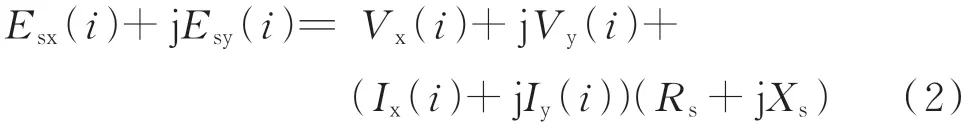
式中：下标x、y 分别表示变量的实部和虚部。需要注意的是，式（2）中采集的监测点数据是基波电压、电流的周期有效值。

分离式（2）中的实部和虚部并分别列写方程，可以分别得到实部方程和虚部方程如下：

对于n组电压、电流数据，根据式（3）和式（4）可各列写n个方程，整理成如下矩阵形式：

将式（5）和式（6）合并，可得：

式中：所有时刻的Vx、Vy、Ix、Iy均已知，共有Rs、Xs、Esx、Esy这4 个未知数。

采用最小二乘法将上式的未知数写在方程左侧，式（7）可以修改为：

式中：“+”表示矩阵的伪逆计算。由于n≥3，则实部和虚部方程至少有6 个，系统参数Rs、Xs有唯一解。

通过式（8），可以对上游系统正序参数进行辨识。

2 电压暂降源上下游定位

短路故障作为引起电压暂降最常见的形式之一，当系统的某一条线路发生短路故障时，相当于在故障点处添加接地支路，系统其他部分的拓扑结构不变。除短路故障以外，造成电压暂降的原因还有很多，如雷击、大容量变压器和电动机的启动等，都可以近似等效为在系统某点处添加接地或者互联支路，系统的总阻抗减小，从而导致电压暂降的发生［18-20］。

上述分析的原理解释如图3 所示，图中：Zs1、Zs2均为系统阻抗；ZL1、ZL2均为负载阻抗；F1、F2为故障点，其中F1位于系统上游，F2位于系统下游；Rf1、Rf2分别为F1、F2处发生故障时的接地电阻，由于大部分情况下接地阻抗呈阻性，因此用接地电阻Rf代替接地阻抗Zf。

图3 电力系统上下游发生故障时系统拓扑结构Fig.3 System topology with faults in upstream and downstream of power system

稳态时，从监测点M分别对系统上下游正序参数进行辨识，上游系统正序参数、下游正序负载参数分别如式（9）和式（10）所示。

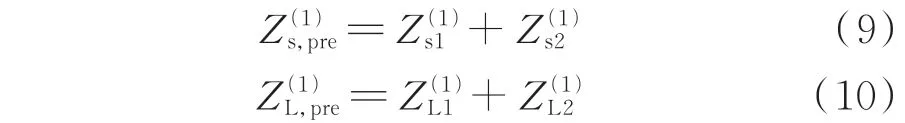
式中：上标“（1）”表示正序参数。

当上游F1位置发生故障时，相当于在F1处增加了接地支路，并通过接地电阻Rf1与大地相连，此时上游正序系统参数发生变化。电压暂降期间上游正序系统参数r的表达式如下：

此时，虽然上游拓扑结构发生了改变，但是下游拓扑结构并未发生变化，因此电压暂降期间下游正序负载参数同式（10），即电压暂降前后下游正序负载参数不变，r=。

同理，当下游F2位置发生故障时，相当于在F2处增加了接地支路，并通过接地电阻Rf2与大地相连，下游正序负载参数发生变化。电压暂降期间下游正序负载参数的表达式如下：

此时，由于上游拓扑结构并未发生变化，因此电压暂降期间上游正序系统参数同式（9），电压暂降前后上游正序系统参数不变，=。

由以上分析可知，当电压暂降源位于上游时，上游系统参数改变，下游负载参数不变；当电压暂降源位于下游时，下游负载参数改变，上游系统参数不变。由于电力系统始终处于动态变化中，它的运行参数时刻都会根据下游负载的变化而做出相应的调整。但是相对来说，上游系统参数较下游负载参数更加稳定，据此，本文提出一种基于上游正序参数比较的电压暂降源定位方法，该方法的主要原理是利用电压暂降前后上游系统正序参数的变化对电压暂降源的上下游位置进行定位。

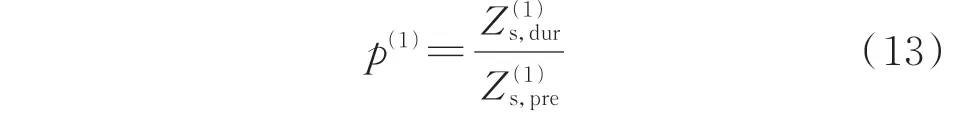
通过理论分析可知，基于上游正序参数比较的电压暂降源定位方法的判据为：当p(1)=1 时，电压暂降源位于下游，否则电压暂降源位于上游。

需要说明的是，上游系统负序、零序参数的变化量也可以用于电压暂降源的上下游定位，可作为辅助判据提高定位的准确性。引起电压暂降的原因很多，但无论哪种原因，在电压暂降期间电压和电流的正序分量一定存在，而负序和零序分量不一定存在，比如：当系统发生三相短路故障时，不存在负序和零序分量，只存在正序分量。所以，采用正序指标进行定位可以保证该方法的适用性。但这并不表示负序、零序判据无法定位，只是在实际应用中，这两种判据在某些情况下无法进行定位。

综上，基于上游正序参数比较的电压暂降源定位方法原理简单，与其他传统的电压暂降源上下游定位方法相比，该方法与下游负载无关，适用于任何负荷模型。除此以外，该方法不区分电压暂降源的类型，无论是短路故障、雷击，还是大容量变压器、电动机启动引起的电压暂降，该方法均适用，适用范围较广。但是该方法也存在不足，例如：在实际情况中，由于参数不确定性、计算误差和测量误差的影响，此时求得p(1)的值接近于1 但是不等于1，导致定位结果出现误判。除此以外，当电压暂降源位于监测点M附近时，实际辨识出的p(1)也接近于1，此时也难以对电压暂降源的上下游位置进行准确的判断。针对以上问题，第3 章将具体讨论解决办法。

3 基于概率的改进判据

对于上文指出的问题——由于实际系统中存在误差和电压暂降源位于监测点M附近时导致p(1)理论上应该等于1 却不等于1 的情况，此处将类似的问题统称为“近区”问题。监测点M的“近区”问题也是制约扰动能量和扰动功率方法等许多传统上下游定位方法准确度的主要原因之一。以扰动能量和扰动功率方法为例，此方法的判据是：当扰动能量DE＜0 时，电压暂降源位于上游；当DE＞0 时，电压暂降源位于下游。但是在包含误差的情况下，如果计算得到的DE值非常接近于0，此时将很难判断电压暂降源的上下游位置。

事实上，近区问题无法得到完全解决。理论分析上，基于上游正序参数比较的定位方法在系统下游发生故障时，上游系统参数本不该发生变化，即p(1)=1。但是实际求得的p(1)值不是确定的数值1，而是在1 附近波动，即在1 附近存在定位的模糊区域。在这个区域内，没有完全的把握能确定电压暂降源位于上游或者下游，武断地给出判断并不科学，可能对上下游双方责任的划分造成不利影响。

为此，本章对第2 章提出的方法做出以下改进：当p(1)位于定位模糊区域内时，判断上下游可能会有误差，所以在p(1)指标的基础上引入概率的思想，当p(1)值接近1 时（如1.01、0.99）由于误差原因无法判断是否位于下游或上游，为了更好地进行责任划分，认为电压暂降源有一定的概率位于上游或下游。

假定包含测量误差、计算误差等在内的综合误差为e（百分比），定义电压暂降源位于上游的概率C(1)up如式（14）所示，该参数的意义为：在定位模糊区域[1-e，1+e]内，由于误差等因素，认为电压暂降源有一定的概率位于下游；否则，认为电压暂降源位于上游。

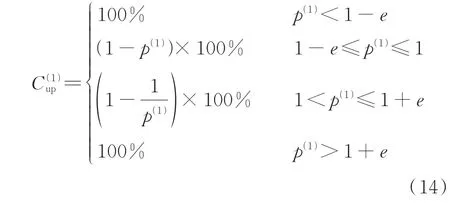
引入概率的思想给“近区”问题提供了一种解决方法，通过计算电压暂降源位于上游和下游的概率，量化了引起电压暂降上下游双方的责任，为电压暂降源的上下游定位提供了理论分析依据，求解步骤如图4 所示。

图4 基于上游正序参数比较的电压暂降源定位方法的求解过程Fig.4 Solving process of voltage sag source location method based on comparison of upstream positive sequence parameters

由于电压暂降源的上下游是相对于监测点的上游和下游划分的，监测点通常安装在负荷的公共连接点处，因此公共连接点所在的网络属于配电网络。一般来说，配电网络是辐射型网络，所以电压暂降源的上下游定位通常针对辐射网而言。当然，环形网络也可以进行电压暂降源的上下游定位，但是由于系统的上游和下游不太明确，因此定位起来相对困难。

4 算例分析

本章采用实际算例验证本文方法的有效性。首先，利用某新能源科技公司的实际电压暂降数据进行方法有效性的验证。之后，采用IEEE Std 399—1997 标准模型对所提方法进行仿真验证，仿真模型如图5 所示。该模型是辐射型网络，上游与外部网络相连，共有两台同步发电机E1、E2，额定电压均为13.8 kV。由于正常运行时个别线路不带载，这种线路不在图5 中表示。

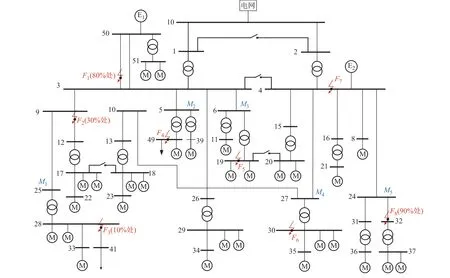
图5 IEEE Std 399—1997 标准模型Fig.5 IEEE Std 399—1997 standard model

4.1 现场电压暂降数据上下游定位验证

某新能源科技公司接线图如附录A 图A1 所示。本文选取了变电站2、变电站7、变电站12 分别在2021 年1 月11 日、3 月18 日 和5 月27 日 的 电 压 暂降数据，5 月27 日电压暂降波形如图A2 所示。通过基于上游参数比较的定位方法、基于等效阻抗实部极性的定位方法、基于扰动能量和扰动功率的定位方法对电压暂降数据进行计算，所得结果如表1所示。

通过表1 可以看出：对于2021 年1 月11 日发生的电压暂降，基于上游参数比较的定位方法和基于扰动能量和扰动功率的定位方法判断为下游，但是基于等效阻抗实部极性的定位方法判断为上游；对于2021 年3 月18 日 和2021 年5 月27 日 发 生 的 电 压暂降，3 种方法均判断发生于上游。由于该现场下游不含源，基于扰动能量和扰动功率的定位方法在此情况下定位精度很高，将本文定位方法计算结果与其做对比，得到的定位结果一致，验证了本文方法的有效性。

表1 现场数据求解结果Table 1 Solving result of field data

4.2 辐射网上下游定位仿真验证

如图5 所示，选取母线25、5、6、27、24 作为监测点，监测点编号分别为M1至M5。在母线11、28、35、36、49 这5 个位置设置感应电机启动。在以下8 个位置分别设置短路故障：线路3-50 的80%处（到母线3 的距离为线路3-50 总长度的80%）、线路9-12的30% 处（到母线9 的距离为线路9-12 总长度的30%）、线路28-41 的10%处（到母线28 的距离为线路28-41 总长度的10%）、母线49、母线19、母线30、母线4、线路24-32 的90%处（到母线24 的距离为线路24-32 总长度的90%），故障点编号分别为F1至F8。每个故障均设置4 种故障类型，Lg、LLLg、LL和LLg 分别表示单相短路、三相短路、两相短路和两相接地短路故障。由于变压器有阻隔电压暂降传播的作用，为了能够监测到电压暂降的发生，对于监测点和故障点之间经过变压器的故障F3、F4、F5、F6，设置它们的接地电阻Rf=10-6Ω；对于监测点和故障点之间未经过变压器的故障，设置它们的接地电阻Rf=0.1 Ω。

先后在系统模型中设置F1至F8这8 个故障和G1至G5这5 个感应电机启动事件，分别获取M1至M5这5 个监测点处电压暂降前后的电压、电流数据，计算 的p（1）结果如表2 和表3 所示，结果保留3 位小数。另外，录波数据采用专门的电压暂降监测设备，每半个周期采样128 次，符合国家标准的要求。

由表2 和表3 可知，上游正序参数的变化量p(1)对4 种故障类型及感应电机启动引起的电压暂降均可以进行定位，且对于任一监测点，同一故障下的4 种故障类型计算得到的p(1)值大小接近但是不相等。当电压暂降源位于监测点上游时，p(1)≫1，其中，F7位置发生单相短路故障时M1监测点求得的p(1)取得最大值，p(1)=37.088；F2位置发生两相接地短路故障时M5监测点求得的p(1)取得最小值，p(1)=2.121。当电压暂降源位于监测点下游时，p(1)≈1，其中，F5位置发生单相短路故障时M3监测点求得的p(1)误差最大，p(1)=1.058；F8位置发生两相接地短路故障时M5监测点求得的p(1)误差最小，p(1)=1.009。根据以上分析可知，本文所提出的基于上游正序参数比较的电压暂降源上下游定位方法能够准确地判断出电压暂降源的上下游位置。

此外，由表2 和表3 分析可知，同一故障点的不同故障类型所引起的电压暂降幅度不同，例如：F1位置发生短路故障时，监测点M4和M5对三相短路、两相接地短路引起的电压暂降可定位，对单相短路、两相短路引起的电压暂降不可定位，这说明了单相短路和两相短路引起的电压暂降幅度较小，不足以引起电压暂降。

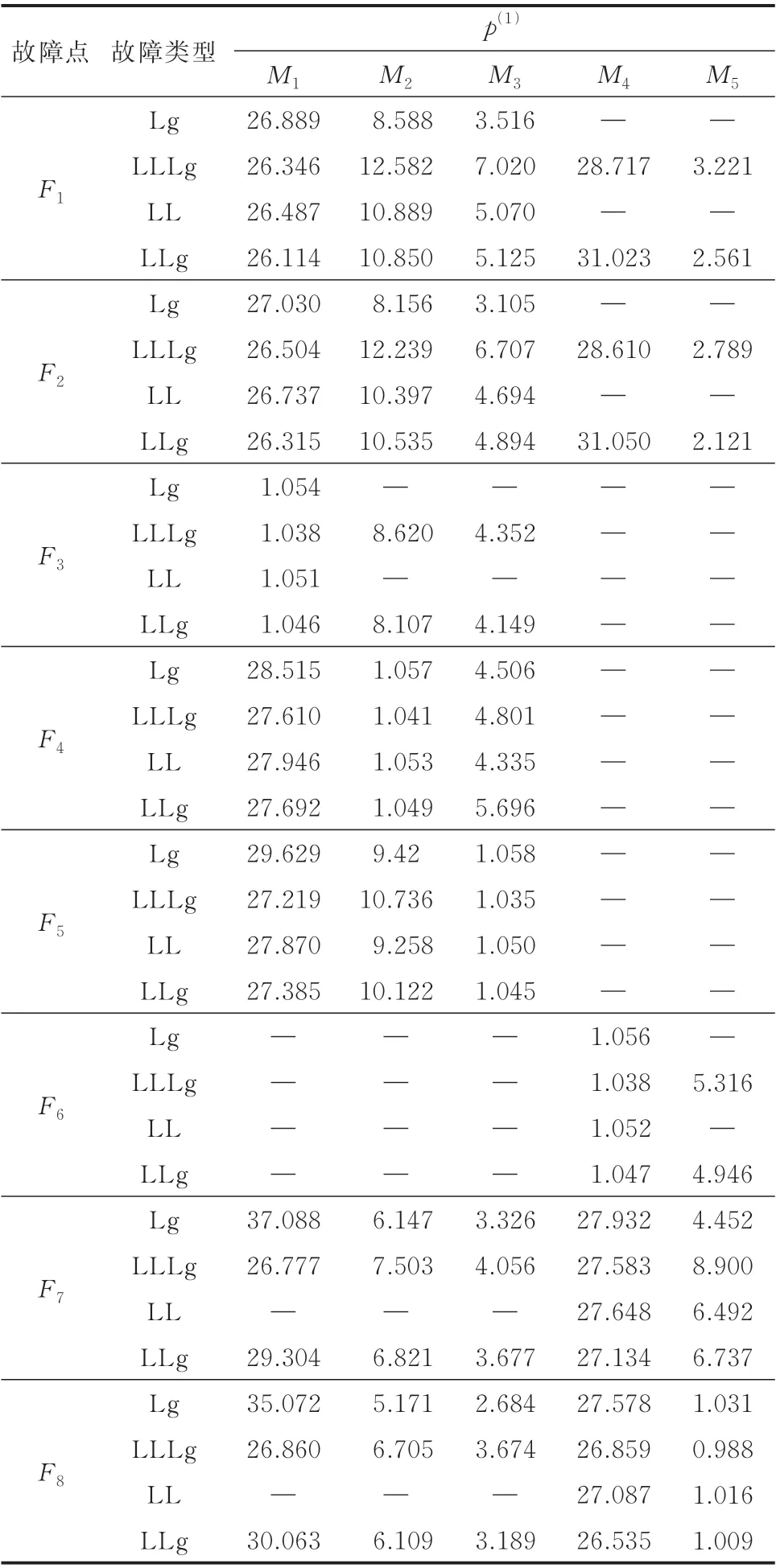
表2 p(1)求解结果Table 2 Sloving result of p(1)

表3 电压暂降源定位结果（感应电机启动）Table 3 Result of voltage sag source location (induction motor start)

从电压暂降可观测性的角度来看，监测点M1至M3对所有短路故障引起的电压暂降可观测性较好，敏感程度高，除F6故障引起的电压暂降不可观测以外，其他故障位置只有部分故障类型不可观测。在实际应用中，M1至M3可选为电压暂降监测点，便于监测全网的电压暂降。相比之下，监测点M4和M5对电压暂降的敏感性较差，只能监测到故障F7、F8和故障F1、F2的部分故障类型，因此在实际中不适合选为电压暂降监测点。

从故障角度分析，由于变压器对短路故障有阻碍的作用，对于监测点和故障点之间经过变压器的短路故障F3、F4、F5、F6，它们引起的电压暂降幅度较小，所以电压暂降的可观测性较差，特别是F6故障，仅有监测点M4对其所有的故障类型全部可观测，监测点M5对其部分故障类型可观测，监测点M1至M3对其全部故障类型均不可观测。这也是本章在监测点和故障点之间经过变压器的故障设置接地电阻较其他故障位置更小的原因。而对于监测点和故障点之间未经过变压器的短路故障F1、F2、F7、F8，监测点M1至M5均可对其引起的电压暂降进行观测。

设综合误差e=6%，不同系统的综合误差取值不同。根据表2 中p(1)的求解结果，可以进一步计算求得电压暂降源位于上游的概率如表4 所示。

以F6位置发生单相短路故障为例，此时只有M4监测到电压暂降。并且通过求解电压暂降源位于上游的概率，可以得知电压暂降源位于上游的概率为5.30%，那么电压暂降源位于下游的概率就是94.70%。通过定量分析上下游双方的责任，更有利于解决电压暂降引起的纠纷。此外，从表4 可以看出，当电压暂降源位于上游时=100%，电压暂降源位于上游的概率为100%，位于下游的概率为0；当电压暂降源位于下游时，0.89%≤≤5.48%，即至少有94.52%的概率认为电压暂降位于下游。整理电压暂降源上下游的定位结果如表5 所示。通过对比仿真模型中监测点和故障点的上下游位置关系和表3、表5 中电压暂降源的上下游定位结果可知，在误差允许范围以内，基于上游正序参数比较的电压暂降源上下游定位方法的准确度为100%。

表4 求解结果Table 4 Solving results of

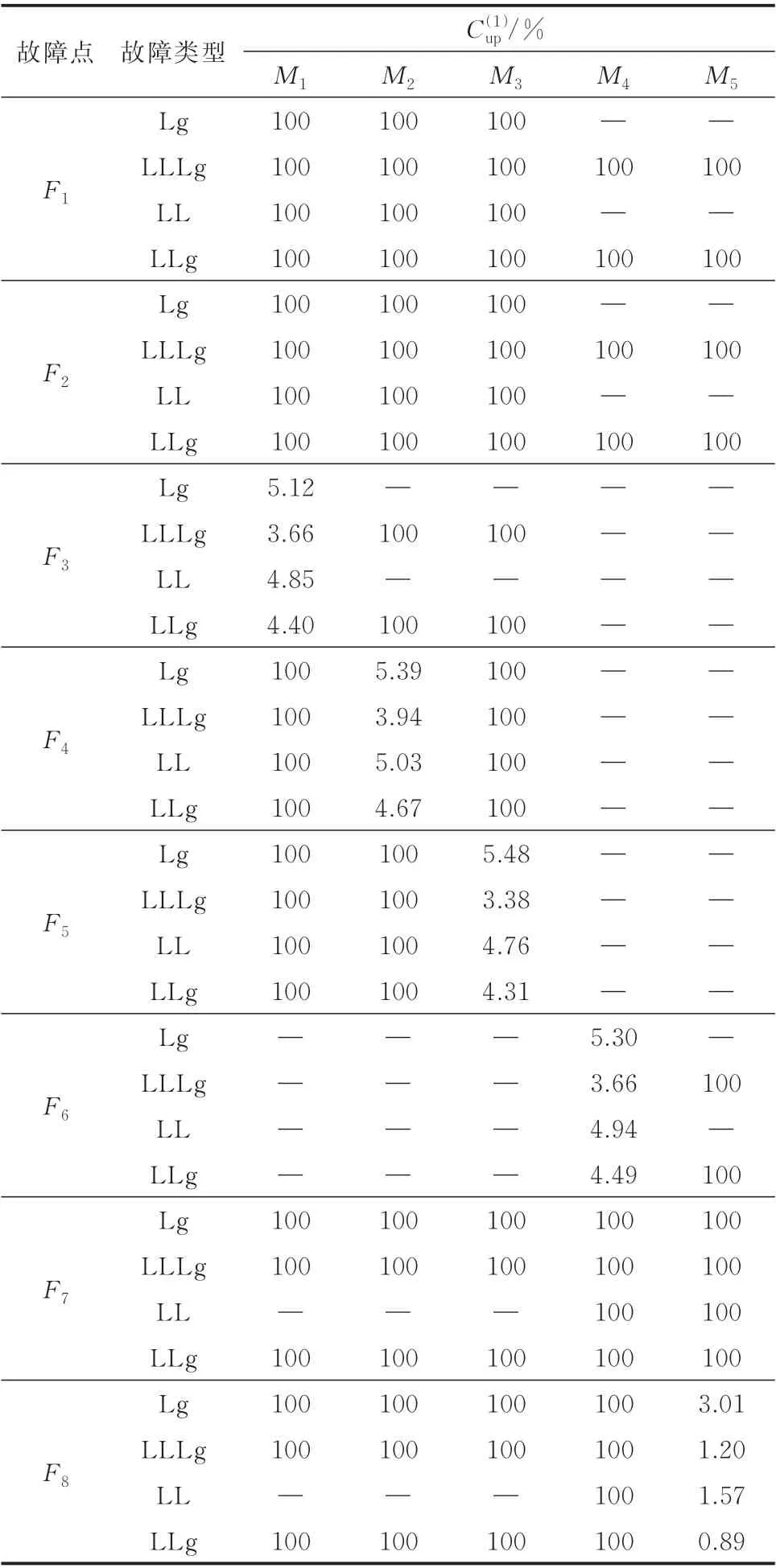
表4 求解结果Table 4 Solving results of

注：表中“—”表示系统中某位置发生故障时，该监测点未监测到电压暂降。

故障点故障类型C(1)up/%F1 F2 M4—100—100—100—100 M5—100—100—100—100 F3 F4 F5 M1 100 100 100 100 100 100 100 100 5.12 3.66 4.85 4.40 100 100 100 100 100 100 100 100 M2 100 100 100 100 100 100 100 100—100—100 5.39 3.94 5.03 4.67 100 100 100 100 M3 100 100 100 100 100 100 100 100—100—100 100 100 100 100 5.48 3.38 4.76 4.31————100—100 100 100 100 100 3.01 1.20 1.57 0.89 F6——————F7 F8 Lg LLLg LL LLg Lg LLLg LL LLg Lg LLLg LL LLg Lg LLLg LL LLg Lg LLLg LL LLg Lg LLLg LL LLg Lg LLLg LL LLg Lg LLLg LL LLg 100 100—100 100 100—100 100 100—100 100 100—100 100 100—100 100 100—100 5.30 3.66 4.94 4.49 100 100 100 100 100 100 100 100

表5 电压暂降源定位结果(短路故障)Table 5 Result of voltage sag source location (short circuit fault)

4.3 与传统电压暂降源上下游定位方法的比较

为了进一步验证本文所提方法的适用性，选择基于等效阻抗实部极性、基于扰动能量和扰动功率两种传统的电压暂降源上下游定位方法与本文所提方法进行比较［18］。本节对短路故障、感应电机启动两种情况进行验证，由于短路故障类型并不影响电压暂降源的上下游定位结果，所以本节只在三相短路下对两种方法进行仿真分析，两种方法中参数的计算结果分别如附录A 表A1 和表A2 所示。

附录A 表A1 及表A2 展示了基于等效阻抗实部极性的电压暂降源定位方法中实部方程、虚部方程分别计算得到的等效阻抗实部Re1、Re2，结果保留4 位小数。根据基于等效阻抗实部极性定位方法的定位判据：当等效阻抗实部Re＞0 时电压暂降源位于上游，当等效阻抗实部Re＜0 时电压暂降源位于下游。由于实部方程和虚部方程均可求得等效阻抗，因此为了统一判据，本文中规定：当实部方程、虚部方程计算得到的等效阻抗实部符号一致时，定位结果准确度较高，实部符号不一致时无法定位。

由附录A 表A1 和表A2 可以看出，基于等效阻抗实部极性的定位方法除了部分故障发生时某些监测点未监测到电压暂降以外，在很多情况下无法对电压暂降源进行定位，主要原因是实部方程和虚部方程辨识出的阻抗实部极性不一致，导致定位结果的准确度较差，只有39.29%。其中，监测点M3和M5的定位结果错误占比较大，可能原因是在该监测点受负荷模型影响较大，因此在未考虑负荷模型的暂态特性时，M3和M5监测点对负荷变动较为敏感，因此定位结果的准确度会受到一定的影响。此外，表A1 和表A2 中部分Re的计算结果接近于0，在实际应用中容易受到误差的影响，导致定位结果错误。

附录A 表A3 与表A4 展示了基于扰动能量和扰动功率电压暂降源定位方法中参数DP、DE的计算结果（DP为扰动功率），该方法的定位判据为：当扰动能量DE＜0 时电压暂降源位于上游，当扰动能量DE＞0 时电压暂降源位于下游。根据上述判据对表A3 和表A4 中的计算结果进行判断，可以看出该方法的定位准确度为58.93%，且DP和DE二者的极性一致。但是，由于本节算例采用的是负荷不含源系统，当负荷含源时，该方法可能会因为功率方向发生改变而导致定位结果错误。此外，由表A3 和表A4 中的数据可以看出，某些DP、DE的值也存在接近于0 的情况，当存在实际应用时很难确定不包含误差下的准确值，导致定位结果错误。

统计上述3 种方法的定位准确度如表6 所示。相比之下，本文所提出的基于上游参数比较的方法通过比较电压暂降前后上游系统正序参数，不受下游负荷模型的影响，适用范围广泛。并且，该方法考虑了误差对电压暂降源上下游定位结果的影响，且在定位模糊区域内引入了概率判据，定量分析了引起电压暂降的上下游双方的责任，更具合理性。

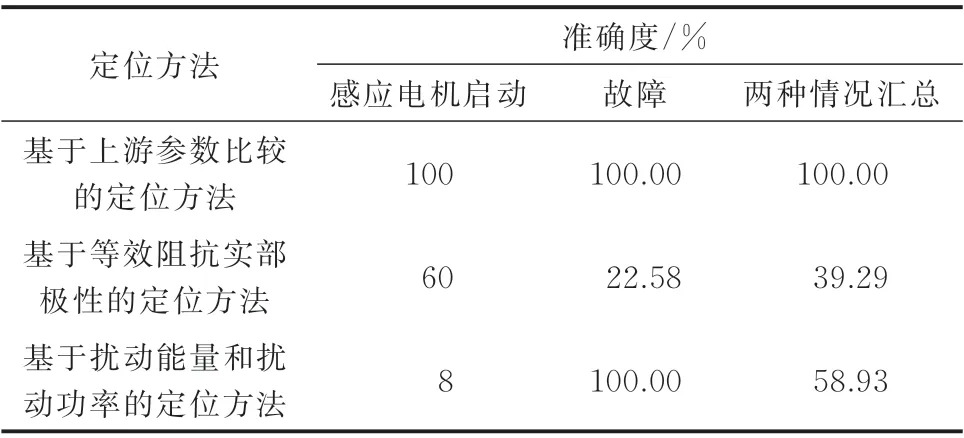
表6 3 种方法的定位准确度Table 6 Location accuracy of three methods

5 结语

本文提出了一种基于上游正序参数比较的电压暂降源定位方法。该方法通过比较电压暂降前后上游正序参数的变化，对电压暂降源进行定位。由于只对上游正序参数进行辨识，不受负荷模型的影响，对所有的负荷模型均适用。除此之外，该方法引入概率的思想对引起电压暂降的上下游双方进行责任划分，为实际应用提供了可靠依据。经仿真验证可知，该方法不易受误差影响，定位准确度较高，适用性好。但目前该电压暂降源定位方法也存在一定的局限性，比如在判据的临界值附近，定位结果的准确度较低，有必要通过改进，提高“近区”范围内电压暂降源定位的准确性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。