参数不对称配电线路的等效模型与接地故障检测方法

刘宝稳，曾祥君，马宏忠，王晨雨，万子雄

（1. 河海大学能源与电气学院，江苏省 南京市 211100；

2. 智能电网运行与控制湖南省重点实验室（长沙理工大学），湖南省 长沙市 410114）

0 引言

中国中压配电网广泛采用非有效接地方式，非有效接地方式下发生单相接地故障仍可继续运行一段时间［1-3］。实际中，配电线路不换位、与配电网有电磁耦合的设备安装不对称等因素造成配电线路对地分布参数不对称；另外，配电线路的类型、材料和安装环境各异，各线路对地分布参数不对称还具有一定的随机差异性［4］。导线坠地、碰树等高阻接地故障的过渡电阻可达10～100 kΩ，配电网发生非金属性接地故障引起的不对称分量微弱，系统三相自然不对称产生的零序电流甚至大于系统单相高阻接地故障引起的零序电流，导致零序电流保护方案的选择性、灵敏性和可靠性受到严重影响。据统计，当前高阻接地故障的检测准确率不足20%［2，5］。

传统电力系统分析和继电保护技术均是在配电网线路三相分布参数严格对称的基础上研究零序电流的特征，认为电网零序电流必须以中性点接地支路为通路［6-7］。然而，受配电线路对地参数不对称的影响，中性点不接地配电网正常运行时各线路依然存在零序电流，这意味着中性点接地支路不是零序电流的绝对流通回路；另外，文献［8］发现非故障线路中的零序电流不一定小于故障线路中的零序电流。以上现象说明传统理论已经不能够解释配电网线路零序电流的形成机理及其特征。文献［9-11］中均涉及配电网的等值运算回路模型，分析了配电网总体分布参数不对称给网络运算带来的影响，但均未把每条配电线路对地分布参数不对称所具有的随机差异性的特征在模型中准确地表达出来。配电网对地分布参数不对称的精准测量已经成为配电网参数测量领域的热点，如文献［9］建立了谐振接地系统的理论等效模型，提出了系统总对地分布参数不对称的测量方法，但不能测量任一指定线路对地分布参数不对称；文献［12］给出接地故障后线路不对称度的表达式，但理论模型中认为线路正常线状态是严格对称的，因此所提出的选线方法无法消除线路对地分布参数不对称的影响。高阻接地故障属于微弱不对称性故障。配电网线路分布参数不对称会严重干扰高阻接地故障的检测。现有接地故障检测方法，如行波法、注入法、暂态特征法、小电阻接地分析法等对高阻故障的检测能力仍不能满足现场要求［13-16］。

现有研究存在以下不足：1）配电网等值运算回路模型不够完善，尚不能准确表达出配电网各线路对地分布参数不对称的随机差异性；2）未凝练出一般化、普遍的配电网线路零序电流理论模型，包括线路产生零序电流的临界条件、一般表达式和流通路径等；3）配电线路分布参数不对称度的在线测量仍未实现，且缺少从配电网局部参量信息中提取出灵敏表征高阻故障信息的方法。

针对以上问题，本文首先提出表征配电线路参数不对称随机差异性的特征参量，研究配电线路零序电流的数学模型、流通回路，给出零序电流产生的临界条件及其物理意义，提出计及线路参数不对称随机差异性的配电网零序网络等值模型。然后，在等值计算模型的基础上，分别给出高阻接地和低阻接地故障下，线路零序导纳、线路对地参数不对称矢量和、线路不对称度等参量的测量方法，并根据配电线路不对称度等参数的测量结果，给出故障选线、选相和过渡电阻测量方法及其优化控制方案。最后，利用MATLAB/Simulink 仿真验证本文提出的配电网零序等值模型及接地故障检测方法。

1 配电网零序网络等值运算模型

1.1 线路参数不对称建模关键参量

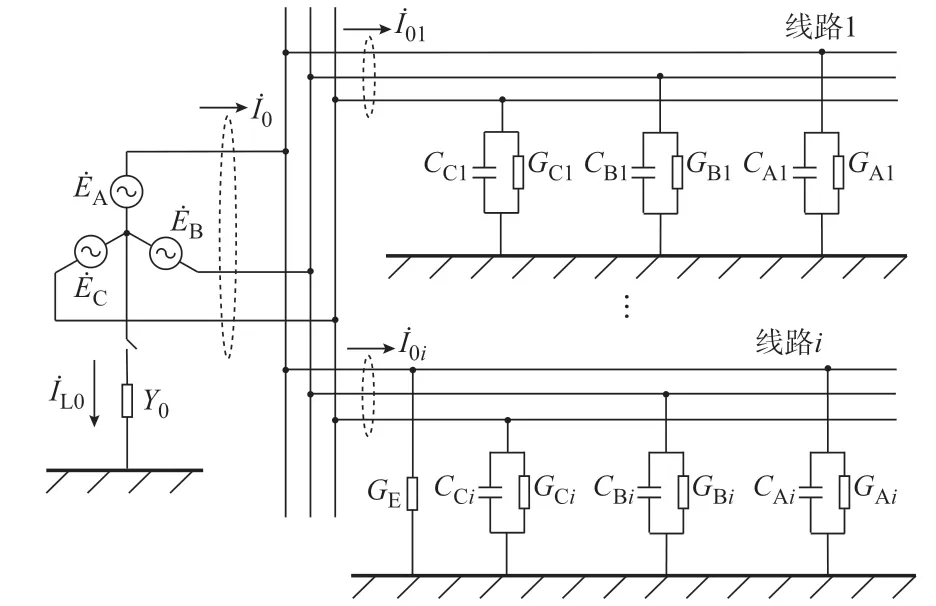
图1 配电网分布参数电路图Fig.1 Distribution parameter circuit diagram of distribution network

若图1 所示配电网中性点直接接地，则接地支路存在自然不平衡电流；若配电网中性点不接地，则配电网存在自然不平衡电压U˙bd。

式 中：YA=jωCA+GA、YB=jωCB+GB、YC=jωCC+GC，其中CA、CB和CC为三相电力线路对地分布总电容，GA、GB和GC为三相电力线路对地分布总电导，ω为系统角频率。由式（1）和式（2）可知，I˙bd和U˙bd为描述配电网分布参数总体不对称的参数。对于含有多条线路的配电网，每条线路的长度、线路性质（架空线或者电缆线等）、布设环境等因素存在差异，导致每条线路参数不对称具有随机差异性。参考式（1）和式（2），建立描述线路分布参数不对称的参数，分别记为线路自然不平衡电流、线路自然不平衡电压。

线路自然不平衡电流定义为：对于含多条线路配电网的任一线路，如图1 中的线路i，若将该线路以中性点直接接地的方式独立运行，线路i分布参数不对称将在接地支路产生不平衡电流。记线路i的线路自然不平衡电流为：

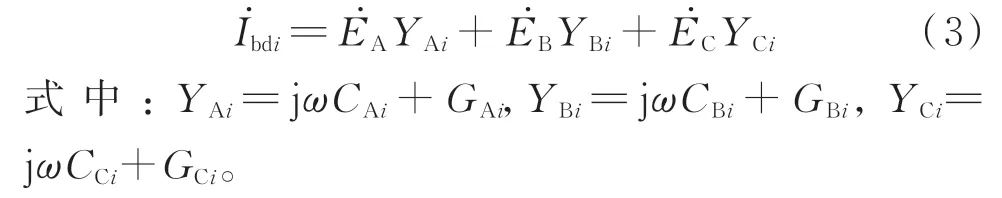
线路自然不平衡电压定义为：对于含多条线路电网的任一线路，如图1 中的线路i，若将该线路以中性点不接地的方式独立运行，线路i分布参数不对称将在中性点形成零序电压。记线路i的线路自然不平衡电压为：

考虑配电网各线路参数不对称的情形存在着随机差异性，每条线路的和均不同。对于含有多条线路的配电网运行时，各线路分布参数不对称相互耦合、共同作用，导致实际运行配电网各线路的零 序 电 流 不 等 于、零 序 电 压U˙0不 等 于，和不属于工程现场可测参量，但却是表征线路自身固有基本特性的参数，对建立配电网零序等值模型有重要的理论意义。

1.2 配电线路零序电流的形成机理

当配电网各线路参数不对称且具有随机差异性时，线路中存在零序电流，并受线路参数的不对称度以及中性点接地方式的影响。以图1 为例，该系统含n条线路，不同接地方式下的Y0取值不同，中性点不接地时Y0=0，经电阻R0接地时Y0=1/R0，经消弧线圈L接地时Y0=1/（jωL），经消弧线圈L并联电阻R0接地时Y0=1/（jωL）+1/R0。电网正常运行时，配电网零序电压为：

根据式（3），线路i的零序电流为：

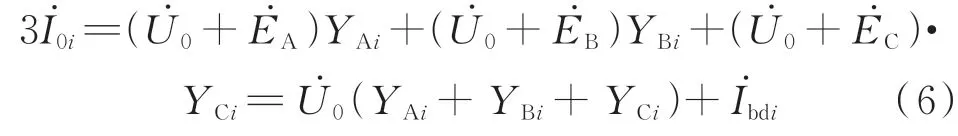
将线路i的代入式（6）可得：

由式（7）可得，配电网线路零序电流的产生机理和物理意义为：不对称电网的线路上自适应产生零序电流，线路零序偏移电压作用在该线路零序阻抗上产生的电流即为线路零序电流，存在线路零序偏移电压是线路产生零序电流的唯一条件。同理，单回线配电网零序电流的形成也服从以上规律。

根据式（4）、式（5）和式（7）可得，图1 中所有n条线路的零序电流之和为：

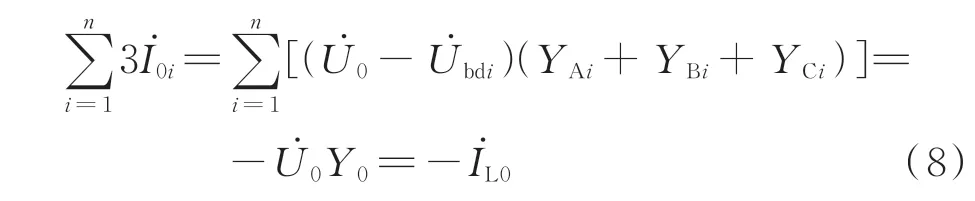
一般认为配电网零序电流必须经过故障点和接地支路之间形成回路［6-7］，这一结论对单回线配电网是成立的，但是对于含多条线路的配电网不再适用。

1.3 配电网零序网络等值模型的建立

配电网零序网络等值模型需要把配电系统总体分布参数不对称、具有随机差异性的配电线路分布参数不对称、配电线路零序电流的形成和流通回路等准确地表达出来。图1 对应的等值计算模型见图2。

图2 中，为了表达配电网总体对地分布参数不对称的影响，配电网零序网络等值运算模型中构造“虚断支路”，将系统零序电压表征为含有无穷大内阻的电压源，即该支路保证母线电压为零序电压U˙0，同时该支路不存在电流（即内阻的电导Y+∞=0，像断开一样）。为了表达每条线路对地分布参数不对称随机差异性的影响，配电网零序网络等值运算模型的每条线路引入线路自然不平衡电压，该电压为各线路以中性点不接地的方式独立运行时的零序电压，即等值运算回路模型的各条线路均引入线路自然不平衡电压。

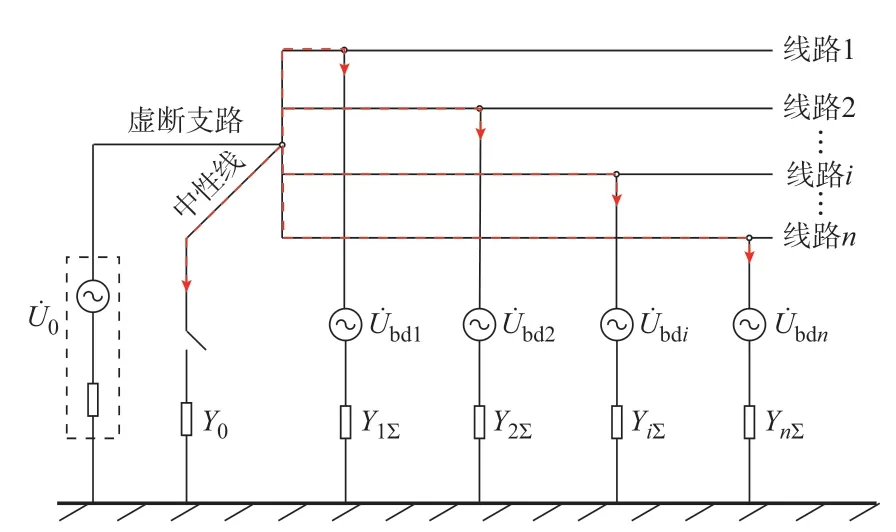
图2 配电网零序网络等值模型Fig.2 Equivalent model of zero-sequence network for distribution network

图2 所示的配电网零序网络等值运算模型中，各线路零序电流和接地支路电流均以母线为公共节点互相流动并满足基尔霍夫电流定律。因此，多线路配电网存在零序电流的回路条件为：线路和接地支路的支路数量之和大于等于2。实际运行中，只有线路和接地支路的支路数量之和大于等于2 时才可能存在线路零序偏移电压。以上从回路条件解释了单回线不接地电网不存在零序电流的原因。

2 单相接地故障检测方法

2.1 线路参数不对称度测量

2.1.1 高阻接地故障

配电网总分布电容和总泄漏电阻是传统配电网参数测量技术的主要研究对象［10，17］。目前尚缺少实现对配电网任一指定线路对地绝缘参数进行测量的方法，包括线路零序阻抗、线路自然不平衡电流、线路参数不对称度等。

由式（7）可知，如果改变加载在被测线路的零序电压U˙0，则线路零序偏移电压Δ随之变化，零序电流也将同比例变化。根据不同接地方式，采取合适的调压方式：1）谐振接地系统采取调节消弧线圈及其串并阻尼电阻的方式［18-19］；2）有源柔性接地系统采取调节注入电流的方式［20-21］；3）有接地变压器的系统采取调节接地变压器绕组分接挡位的方式［14］；4）中性点不接地系统可以采用在线路侧接入偏置元件等方式［22-23］。

图2 中，若线路i为被监测的线路，记当前状态下的零 序电压 为，线路零序电流为；调 整电网零序电压为，测取零序电压调整后的线路i的零序电流，其 满足：

整理式（9）和式（10）得线路i的零序导纳Yi为：

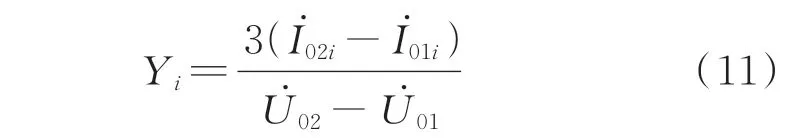
记线路i对地参数不对称矢量和为k0i=YAi+α2YBi+αYCi，α=e120°，k0i反 映 了 线 路i三 相 对 地 绝缘参数的不平衡性，属于评价线路对地参数不平衡性的重要参量。为了计算线路i对地参数不对称矢量和k0i，将式（4）的线路自然不平衡电压U˙bdi代入式（10），整理可得：

将Yi代入式（12）可得：

变换式（13）可得线路i自然不平衡电流=k0i。由式（11）和式（13）可知，只需要测量零序电压调整前后被测线路零序电流的变化量即可实现线路零序导纳、线路对地参数不对称矢量和、线路自然不平衡电流的测量。

根据不对称度的定义，由式（11）和式（13）可求得线路i的不对称度ρi为：

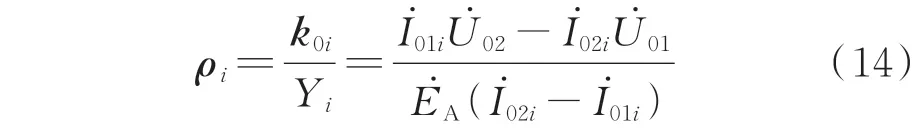
实际中，高阻接地故障引发配电网零序电压和线路零序电流变化量均很小，接地故障电流也相对较小，提高故障检测灵敏度较为关键。因此，可通过人为的方式增大配电网零序电压和各线路零序电流的变化量，以提高式（11）、式（13）和式（14）的计算准确度。

2.1.2 低阻接地故障

低阻接地故障（甚至金属性接地故障）的发生率较高，低阻接地的故障电流大，故障后再进行调压测量线路对地分布参数及其不对称度将延缓接地电流补偿装置的动作时间，提高接地电流消弧的快速性是首先需要解决的问题。本文利用低阻接地故障引起的配电网零序电气信息变化量大的特征，仅利用故障自身引发零序电压和零序电流的变化量计算出检测接地故障的特征参量。

若电网线路i的A 相发生单相接地故障，故障过渡电导为GE。单相接地后电网零序电压为。线路i在故障后的零序电流为；正常线路s在故障 前 的 零 序 电 流 为，故 障 后 的 零 序 电 流 为。利用式（11）计算正常线路和故障线路的零序测量导纳分别为YsE、YiE：

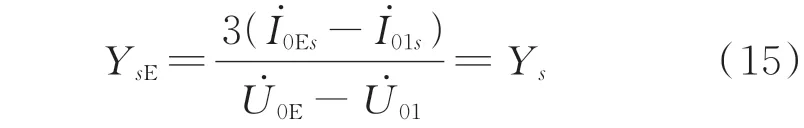
式中：Y0Σ=YA+YB+YC+Y0为配电网总零序导纳；Ys为线路s的零序导纳。由式（15）和式（16）可知，对于正常线路s，故障前后线路零序电流变化量与零序电压变化量的比值依然等于自身线路零序导纳；对于故障线路i，故障前后线路零序电流变化量与零序电压变化量的比值等于自身线路零序导纳与系统总零序导纳的差。若电网仅有2 条线路，且线路参数相近，则仅根据式（15）和式（16）的计算结果无法准确区分故障线路。然而，不论配电网有几条馈线，故障线路的不对称度很大，正常线路不对称度保持不变，根据不对称度寻找故障线路是最灵敏的手段。

同理，利用式（13）分别计算正常线路和故障线路的对地参数不对称矢量和k0sE和k0iE：

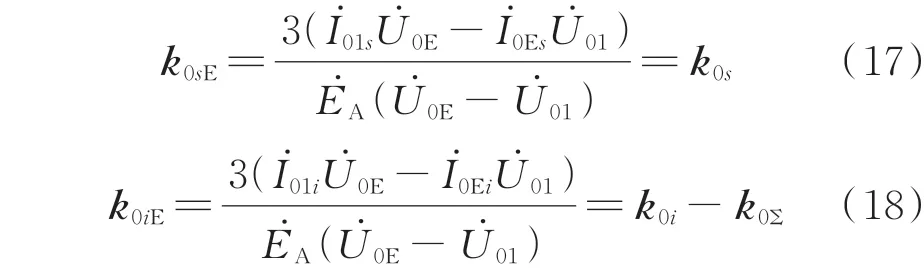
式中：k0Σ为配电网总对地参数不对称矢量和。

由式（17）和式（18）可知，对于正常线路，根据故障前后的零序电压和零序电流计算得到的对地参数不对称矢量和等于该线路自身的值；对于故障线路，该计算值为线路自身对地参数不对称矢量和与系统总对地参数不对称矢量和的差值。

由式（15）和式（17）得到正常线路的不对称度ρs为：

由式（19）可知，正常线路参数不对称度的计算结果不变，依然等于线路自身的不对称度。对于故障线路i，由式（16）和式（18）得到不对称度ρi为：

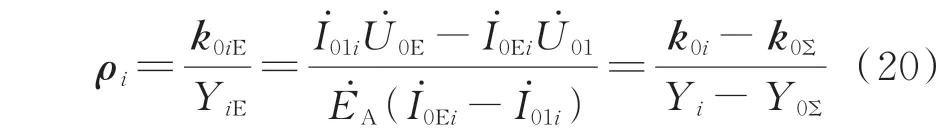
由式（20）可知，故障线路i的计算不对称度为电网切除线路i后剩余部分的不对称度。因此，线路零序导纳、对地参数不对称矢量和、不对称度这3 个参数均可以作为故障选线的依据。

由以上分析可知，根据式（16）和式（20）并不能直接求出故障线路的零序导纳和不对称度，为此提出仅依据故障前后零序电压和故障线路零序电流的直接计算方法。设线路i发生单相接地故障，则该线路故障后的零序导纳YiE=Yi+GE、故障后的线路自然不平衡电流=k0i+GE，其中为故障相电源电势。计算故障线路i的不对称度ρiE的关键在于对YiE、进行计算，由这2 个参数的表达式整理得到第1 方程式为：

式（21）中，仅YiE和是未知数，其他参数均可通过计算求得（或为已知量），需要再建立一个包含2 个参数的方程组，求解二元一次方程组即可。第2 个方程可以由故障后零序电压，或者系统任一线路或多个线路的零序电流计算式求得。推导发现，选择不同的第2 方程式，YiE与的表达形式存在较大区别，物理含义不同但数学含义相同。以故障后的零序电压推导得到第2 方程式为：

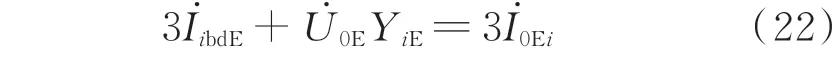
由式（21）和式（22）求得YiE和分别为：

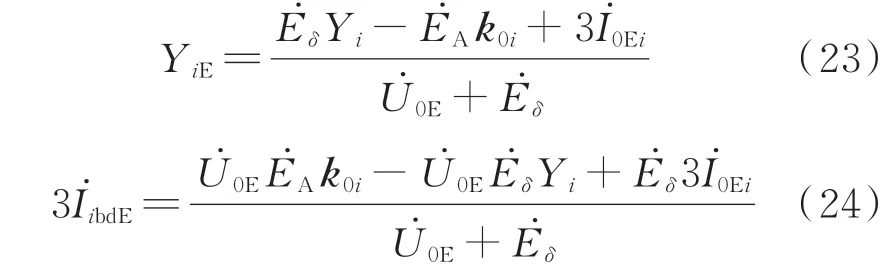
则故障线路i的不对称度为：

若A 相接地则故障线路i的不对称度为：

实际应用时，低阻接地故障引发配电网零序电压和线路零序电流变化量均较大，接地故障电流也相对较大。直接利用故障前后零序电压和线路零序电流计算故障线路的不对称度，免除故障后再调压带来的延时，保证了故障检测和消弧的快速性。

2.2 单相接地故障灵敏检测方法

2.2.1 线路不对称度对过渡电阻的反映能力

单相接地故障属于不对称性故障，过渡电阻可以显著改变线路三相参数不对称度这一参量。因此，利用不对称度这一参量检测故障是一种新尝试。

对于线路i，正常状态下的不对称度为：

式中：Ci为线路i的三相分布总电容；Gi为线路i的三相分布总电导。若线路i的三相分布参数对称（或近似对称），则|k0i|=0、|ρi|=0。当线路A 相发生单相接地故障，过渡电导记为GE，则线路的不对称度为：

根据式（27）和式（28），得到过渡电阻引起线路不对称度的变化量ρiΔ为：

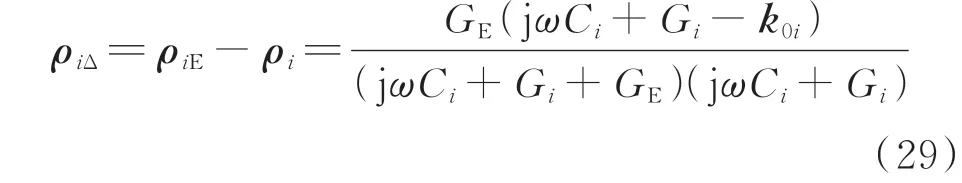
国家标准GB/T 15543—2008《电能质量 三相电压不平衡》中规定，电网正常运行时负序电压不平衡度不超过2%（保证不平衡负荷的最大工作周期包含在内）。电缆线路的不对称度更低，甚至小于0.5%。若忽略线路正常状态的不对称，过渡电阻引起线路不对称度的变化量为：

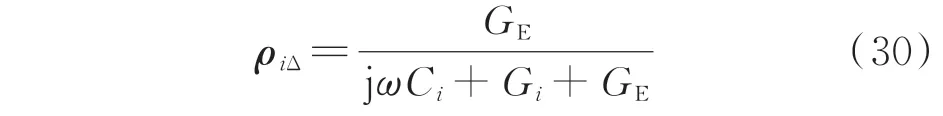
由式（30）可知，金属性接地故障时，GE→∞，|ρiE|=100%；接地电阻无穷大时，GE=0，|ρiE|=0。因此，接地电阻越小，线路的不对称度变化越大，且过渡电阻对线路不对称度的改变范围为0～100%。考虑|ρi|的理论最大值为3.5%，过渡电阻对线路不对称度的改变范围约为3.5%～100%。为了防止误动作，在利用线路三相参数不对称度进行故障检测时需要躲开最大不对称度3.5%。

另外，线路三相分布总电容和总电导也是影响过渡电阻引起线路不对称度变化的因素。对式（30）中的Yi求导数可得：

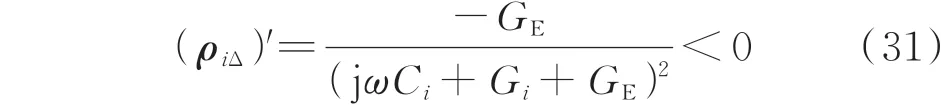
由式（31）可知，随着线路三相分布总电容和总电导的增加，过渡电阻引起线路不对称度的变化量越小，即线路越短，利用线路参数不对称度检测故障越灵敏。10 kV配电网供电半径一般不超15 km，以每千米线路对应1.3 A 电容电流为例，15 km 线路的电容电流为19.5 A，分布电容的容纳为0.003 377 S，则引起线路不对称度变化量为3.5% 的过渡电阻值为8 459.34 Ω，即最大检测的过渡电阻为8 459.34 Ω。若线路长度缩短，如5 km 线路的电容电流为6.5 A，分布电容的容纳为0.001 126 S，则最大检测的过渡电阻为25 378.78 Ω。因此，线路不对称度有着灵敏反映过渡电阻的能力，且线路长度越短，耐受过渡电阻的能力越强。

2.2.2 故障识别与选线

1）高阻接地故障。虽然高阻接地属于微弱不对称性故障，但仅会对故障线路对地分布参数不对称造成明显改变。跟踪配电线路对地分布参数不对称度的变化趋势，并从中提取出故障特征信息进行故障检测是提升高阻接地故障检测灵敏度的有效手段。

一般情况下，电网线路不对称度通常为0.5%～1.5%，理论极限为3.5%。当配电网发生接地故障后，故障线路对地分布参数不对称度将发生变化，而正常线路对地分布参数不对称度保持不变。因此，通过监测线路对地分布参数不对称度的变化，并根据线路对地分布参数不对称度的变化量超过一定阈值来判定故障线路。考虑配电网的自然不对称度一般不超3.5%以及现场传感器误差的影响，引入可靠性系数τ(τ＞1)，则判定线路是否发生故障的阈值设定为3.5%τ，而可靠性系数τ的设定需要躲过线路最大自然不对称度以及传感误差带来的误差值。

若电网正常运行时通过式（14）计算的配电线路不对称度较大，可以跟踪线路不对称度的变化量ρiΔ来识别高阻故障。同样，考虑测量误差等因素的干扰，将判定线路是否发生故障的ρiΔ阈值设定为3.5%τ。

2）低阻接地故障。若单相接地故障的过渡电阻较小，故障形成较大的零序电压偏移量，零序电压增量大于15%相电压作为判定发生低阻接地故障的依据。由式（19）和式（20）计算得到的正常和故障线路参数的不对称度有着明显的区别，正常线路的不对称度保持不变、故障线路的为电网切除线路i后剩余部分的不对称度；此外，由式（26）得到故障线路的不对称度最大。因此，可据此选择故障线路。

3）特殊情形。当配电网存在断路器等开关设备三相分合闸不同期、单相自动重合闸以及非全相运行等严重不对称运行的情形时，需要闭锁故障检测。

2.2.3 过渡电阻测量与故障相选择

若系统发生接地故障，以A 相发生单相接地故障（过渡电导为GA）为例，故障后的第i条线路自然不 平 衡 电 流为：

线路故障前后自然不平衡电流的变化量为：

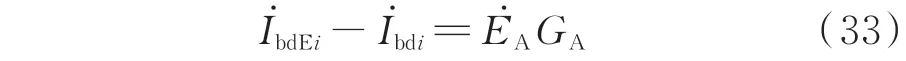
由式（33）可知，线路故障前后自然不平衡电流变化量的相位与电源电势的相位相同，基于此可以实现故障相的选择。另外，过渡电导等于线路故障前后自然不平衡电流变化量与电源电势的比值，基于此可以实现过渡电导的测量。

为了更清晰地说明式（33）所表达电气量之间的关系，图3 为线路i的A 相发生单相接地故障后接地电导与线路零序阻抗的矢量关系图。

图3 中，线路正常状态下A 相的零序导纳为YAi，由于线路对地参数呈阻容性，YAi的相位超前相电压近90°，且线路对地参数不对称矢量和为k0i（图3 中黑色实线箭头）。但是当A 相发生单相接地故障后其零序导纳变为YAiE，YAiE与相电压的夹角因过渡电导GA的影响而变小。故障后，线路对地参数不对称矢量和变为k′0i（图3 中红色实线箭头）。

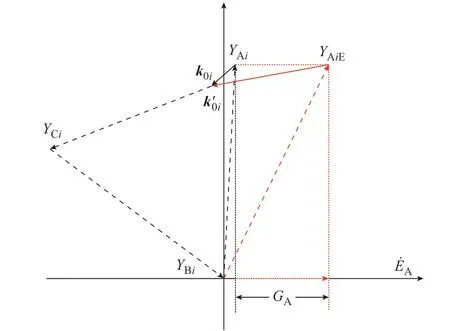
图3 接地电导与线路零序阻抗的矢量关系Fig.3 Vector relationship between grounding conductance and line zero-sequence impedance

由图3 得出：

2. 3 故障检测控制方案

本文研究了配电网线路不对称度等参数测量方法、基于线路不对称度的单相接地故障选线、过渡电阻计算与故障选相方法，具体流程见附录A 图A1。在配电网正常运行时，主动调节配电网零序电压，通过式（11）、式（13）和式（14）计算配电线路的零序导纳、对地参数不对称矢量和、不对称度等参量，并实时监测配电网零序电压。

若配电网零序电压增量较大且超过15%的相电压，可以判定发生单相接地故障且过渡电阻较小。采集故障前后的零序电压和被检线路零序电流，先通过式（19）和式（20）计算各线路的不对称度，不对称度变化的线路为故障线路，然后利用式（26）计算出故障线路的真实不对称度。

若配电网零序电压增量较小且小于15%相电压，可通过人为调压的方式增大零序电压和线路零序电流，然后由式（11）、式（13）、式（14）和式（30）计算配电线路的零序导纳、对地参数不对称矢量和、不对称度和不对称度变化量等参量，其中线路参数不对称度（或其变化量）大于3.5%τ的为故障线路。继而，根据式（33）和式（34）选择故障相并计算过渡电阻。通过人为短时干预零序电压进行高阻故障的主动识别与选线，考虑调压暂态时间一般不超3 s，一次检测流程可在5 s 左右完成。

实际应用中，若配电网存在非全相运行等特殊不对称运行工况，需要闭锁故障检测；若配电网运行方式改变，只需要立即对新投入、长度或类型变化的线路进行跟踪监测。

配电网正常运行和高阻接地故障时，人为增大零序电压可减小测量误差，增大线路参数不对称度的计算准确度。但过大零序电压不利于配电网的安全运行，参考国家标准GB/T 50064—2014《交流电气装置的过电压保护和绝缘配合设计规范》的规定：正常运行时，自动跟踪补偿消弧装置应确保中性点的长时间电压位移不超过系统标称相电压的15%。因此，调压目标值设定为15%相电压，即若当前零序电压为，调压目标值为15%，则电压调节量Δ为：

考虑频繁调压不利于电网安全，根据小电流接地系统单相接地故障后允许运行1～2 h 的规定，建议每隔1 h 进行一次高阻故障检测。根据式（35）可知，零序电压调节量满足国家标准对零序偏移电压长时间运行的要求，若对高阻故障检测快速性有更高要求，可以缩短调压间隔时间。

3 仿真验证

利用MATLAB/Simulink 仿真验证本文提出的零序电流产生机理的数理建模与线路接地保护新方法。仿真系统为含有3 条线路的10 kV 配电网（如图4 所示），参数设置见附录A 表A1［3］，表A1 给出每条线路和系统的对地分布参数和阻尼率。

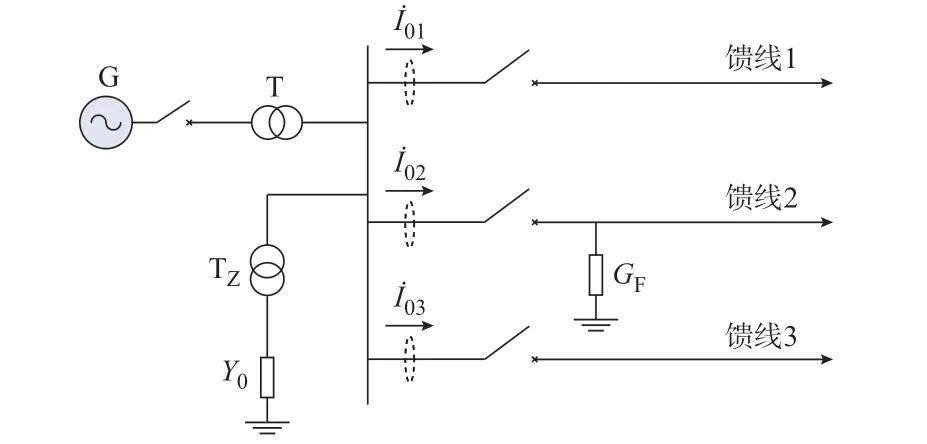
图4 仿真系统拓扑Fig.4 Topology of simulation system

1）零序电流产生机理的仿真实验。仿真设置了3 种中性点接地方式，即中性点不接地、经高阻（接地电阻为800 Ω）接地、经消弧线圈（过补偿15%）接地。通过调整中性点接地导纳改变仿真系统的零序电压，从而改变了各线路的零序偏移电压。附录A表A2 至表A4 给出了3 种接地方式下通过式（7）计算出各线路的零序电流理论计算值，然后与仿真系统测量值做误差分析。由附录A 表A2 至A4 可知，本文建立的计及线路参数不对称随机差异性的配电网零序网络等值运算模型能准确计算出不同接地方式下各配电线路的零序电流。

2）线路对地绝缘参数测量的仿真实验。为了验 证 线 路 绝 缘 参 数（包 括Yi、k0i、和 不 对 称 度ρi）测量的准确性，调节仿真系统的零序电压，测取调压前后线路零序电流，然后代入式（11）、式（14）计算，并将计算结果与所设置实际值做误差分析。考虑k0i与满 足=k0i，仅 对做 仿 真 验 证。采 取调整中性点接地阻抗的方式改变零序电压，具体为中性点经800 Ω 电阻接地和经消弧线圈（过补偿15%）接地，仿真结果见附录A 表A5 至表A7。所提方法可较为准确、独立地测量配电线路绝缘参数，包括线路零序导纳、线路参数不对称度等，且各线路间互不干扰，也不受中性点接地方式的限制。

3）高灵敏度线路接地保护新原理的仿真实验。为了验证基于线路不对称度测量的故障判定与选线方法，在线路2 的A 相设置了高阻接地故障。同时，为了验证方法耐受过渡电阻的能力，将过渡电阻设置为3 000 Ω，则线路2 单相接地故障后的理论不对称度（仿真设置值）为3.61%，超过了线路不对称度的理论极限3.5%。采取调整中性点接地阻抗的方式改变零序电压，具体为中性点经800 Ω 电阻接地和经消弧线圈（过补偿15%）接地，测量调压前后的系统零序电压和线路零序电流，计算各线路的不对称度，并根据线路不对称度是否超过理论极限3.5%进行故障选线，结果见附录A 表A8。

为了验证过渡电阻计算与故障相选择准确性，在仿真系统中线路2的A相设置了过渡电阻为1 500 Ω的高阻接地故障，在中性点不接地、经800 Ω 接地和经消弧线圈过补偿15%接地3 种接地方式下，通过中性点接地支路并接1 000 Ω 中性点接地电阻的形式调节故障前后的零序电压，计算线路2 故障前后的 自 然 不 平 衡 电 流和，然 后 根 据 线 路 故 障 后不平衡电流的变化量计算接地电导。根据计算出的相位和幅值分别实现故障选相和过渡电阻测量，结果见附录A 表A9。表A8 和表A9 中，线路参数不对称度能灵敏反映过渡电阻的参量，通过监测线路不对称度可有效选择故障线路和故障相，并准确计算过渡电阻。

4 结语

本文在计及电网三相分布自然不对称的基础上建立了配电网零序网络等值运算模型。提出了配电线路零序阻抗和不对称度等绝缘参数的测量方法。给出了单相接地故障选线、故障选相和过渡电阻测量方法。故障检测以线路为检测单元，无须进行线路间电气信息比较。根据故障程度不同，高阻接地故障优先保障故障检测的灵敏性，低阻接地故障优先保障故障检测的快速性。配电网的运行状态发生变化时，如运行方式改变、线路停复电等，只需要对新投入的线路和母线进行跟踪监测即可，其他未受运行方式改变的线路不需要特殊处理。接地故障检测方法耐受过渡电阻的能力强、物理意义清晰、实施方便。下一步将研制原理样机，并进行真型模拟实验和工程应用试点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。