基于FPGA 的变流器并行多速率电磁暂态实时仿真方法

李 珂，顾 伟，柳 伟，曹 阳，楼冠男，邹德虎

（1. 东南大学电气工程学院，江苏省 南京市 210096；2. 南京理工大学自动化学院，江苏省 南京市 210094）

0 引言

随着分布式发电和交直流混联等技术的发展，电网的电力电子化程度不断提高，网络中功率流动和暂态过程的分析更加复杂［1］，需要模型更完善、计算精度更高的仿真系统对网络特性进行研究。以变流器为代表的电力电子设备越来越多地融入电力系统中，其中部分开关器件的工作频率可高达104Hz以上，需要微秒级的仿真步长反映其暂态过程，大大增加了仿真系统的计算负担。

在仿真计算效率和计算机计算能力有限的前提下，实时化电磁暂态仿真的仿真规模、仿真精度和计算速度难以得到兼顾。为了满足变流器模型中快动态的开关元件对微秒级仿真步长的需求，RT-LAB等商业仿真平台从底层硬件的角度对仿真系统进行了 改 进［2-3］，通 过 引 入 现 场 可 编 程 门 阵 列（field programmable gate array，FPGA）进一步优化系统的计算性能，以实现电磁暂态仿真的实时化。文献［4-5］采用一种基于伴随离散电路（associated discrete circuit，ADC）开关模型的电磁暂态实时仿真计算方法，利用该模型下导纳矩阵不随开关状态变化的特性在FPGA 中进行实时仿真计算。文献［6］基于ADC 开关模型实现了光伏发电系统的暂态仿真，并提出了控制器、光伏电池等元件在FPGA 中的建模方法，对仿真步长与结果误差的关系进行了研究。文献［7-8］通过计算所有开关可能的状态组合并预存每种状态下的系统导纳矩阵，反映了开关状态变化对系统的影响。以上基于FPGA 独立实现的电磁暂态仿真存在以下问题：

1）采用ADC 开关模型带来了虚拟功率损耗问题［9］，通过预存导纳矩阵反映开关状态时程序占用的存储空间随开关元件的数量迅速上升［10］；

2）FPGA 成本较高且硬件资源有限，一定程度上限制了仿真网络的规模；

3）网络控制策略和系统参数的调整过程较为复杂，对实时仿真的灵活性造成了限制。

文献［11］提出一种基于CPU-FPGA 异构平台的逆变器实时仿真方案。该方案结合不同计算单元的优势，对变流器模型进行解耦后将控制系统的计算由基于CPU 的服务器实现，其余计算由FPGA 实现，在保证实时性的前提下降低了FPGA 的硬件资源消耗，但在不同步长时序配合的过程中，直接以对侧最后一个仿真步长的结果作为输入，没有进一步考虑多速率解耦并行仿真过程中的时序误差。本文提出一种变流器电磁暂态硬件加速实时仿真方法，通过对并行仿真时序下控制系统解耦的多速率仿真误差进行分析，采用结合拉格朗日插值的改进线性插值算法得到更精确的计算结果，并基于FPGA 实现了电磁暂态实时化硬件加速仿真计算，建立了计算能力更强的实时仿真系统。最后，本文搭建了三相桥式逆变器模型算例对所提出仿真方法的性能进行分析，并将仿真结果与PSCAD 离线仿真结果进行对比，验证了实时仿真结果的准确性。

1 控制系统解耦的多速率并行计算方法

与工作状态高频率变化的开关元件相比，变流器控制系统的动态特性更接近于变流器以外的慢动态网络，实现控制系统的多速率解耦仿真可以在反映高频暂态过程的同时有效提高仿真计算效率。本章重点介绍变流器控制系统与电气状态解耦求解的多速率并行计算方法。

1.1 多速率并行计算时序分析

实现变流器控制系统与电气状态解耦计算时，需要将离线仿真中的控制系统与电气状态从以单一步长串行求解的仿真时序转变为以不同步长并行求解的仿真时序。图1 反映了不同电磁暂态计算时序的对比，图中的箭头表示依次发生的数据计算或传输过程。

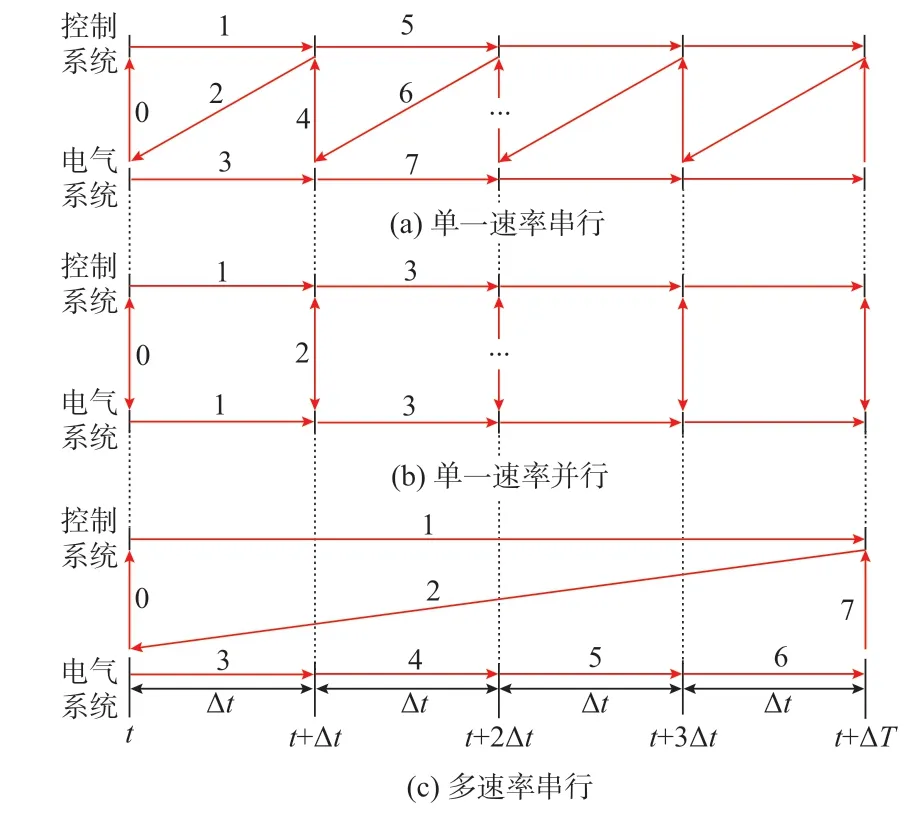
图1 电磁暂态计算时序示意图Fig.1 Schematic diagram of time sequence of electromagnetic transient calculation

设变流器控制系统采用较大仿真步长ΔT进行仿真，而电气状态采用小步长Δt求解，其中ΔT为Δt的整数倍，定义其倍数δ=ΔT/Δt为步长倍率（以δ=4 为例），将大小步长之间的数据交互设置在每个大步长的起始时刻进行。可以看出，仿真时序的转变将在两方面产生计算误差：

1）控制系统由串行计算时序转变为并行计算时序增加的延迟误差［12］。对比图1（a）和（b）中t+Δt到t+2Δt时刻的电气状态求解过程可以发现，单一速率串行时序下，该时间段求解时使用的控制参数以t+Δt时刻的电气状态为基础在过程5 中计算得到，经过程6 传递到电气系统侧；而在单一速率并行时序下使用的控制参数根据t时刻的电气状态在过程1 中得到，经过程2 传递到电气系统侧，由此控制系统的计算产生一个步长的额外延迟，对结果的准确性造成影响。

2）单一速率仿真转变为多速率仿真产生的延迟误差。对比图1（a）和（c）可知，采用多速率串行时序替代单一速率串行时序时，大步长仿真计算的频次低于小步长仿真，因此，并非每个小步长仿真计算采用的大步长侧输入量都是对应时刻的实际值。即多速率仿真过程中，变流器控制系统的变化对于电气系统计算的影响将无法得到完全反映，由此产生了相应的计算误差。当不同时间常数的系统之间动态特性差异更小时，或者大小步长之间的倍数更大时，该问题产生的误差将更加显著。

1.2 结合拉格朗日插值的改进线性插值算法

产生以上误差的根源在于，并行时序下多速率仿真计算中对侧的实时数据难以得到准确表示，需要结合插值算法对对侧实时数据进行有效预测，补偿控制系统在一个大步长对应的多个小步长下的变化，减小多速率并行计算过程中的误差。文献［13］采用线性内插计算一个大步长所对应的多个小步长时刻慢动态网络的历史状态，解决了多速率网络解耦计算时，小步长侧历史电流源计算所需的前一时刻慢动态网络状态未知的问题，但内插法只能用于已知区间内，无法将插值范围扩大到未计算的时刻。外插法是一种根据已知的离散数据集合对范围外的数据进行预测的插值方法，利用先前时刻的已知结果通过插值对未来时刻的结果进行估计可达到减小延迟误差的效果。文献［14］采用单次线性外插预测电气状态，降低了计算时序由串行转变为并行所增加的延迟误差。这种方法具有形式简洁、计算量小的优势，在步长极小的情况下具有较好的数值稳定性［15］。但文献［14］没有对多速率仿真场景下的误差补偿做进一步分析，在多速率仿真步长倍率较大时准确性有所下降。

本文提出一种结合拉格朗日插值的改进线性插值算法。首先，采用两次迭代外插扩大已知区间，再使用拉格朗日内插法得到下一大步长所对应的各小步长时刻下控制系统的状态，并以此为依据计算开关状态，在下一大步长开始时将结果传递至电气状态求解侧，对控制系统解耦后的多速率仿真及并行仿真计算过程中的两方面误差做进一步补偿，最后得到更准确的计算结果。

图2 反映了本文所提出改进线性插值算法的计算时序。图中，黄色部分和红色部分分别代表t―ΔT到t时刻，以及t到t+ΔT时刻变流器控制系统的计算过程，蓝色部分代表t到t+ΔT时刻电气状态的求解过程。

图2 改进线性插值算法时序示意图Fig.2 Schematic diagram of time sequence of improved linear extrapolation algorithm

从t到t+ΔT时刻，控制系统计算过程具体如下：

步骤1：接收t-ΔT到t时刻电气系统的计算结果。

步骤2：根据t时刻的电气状态计算该时刻下控制系统的输出vmod（t）。

步骤3：基于vmod（t）以及先前t-ΔT和t-2ΔT时 刻 的 控 制 系 统 输 出 量vmod(t-ΔT)、vmod(t-2ΔT)，采 用 两 次 迭 代 插 值 对t+ΔT和t+2ΔT时刻的控制系统输出量vmod（t+ΔT）、vmod（t+2ΔT）进行预测，如式（1）所示。

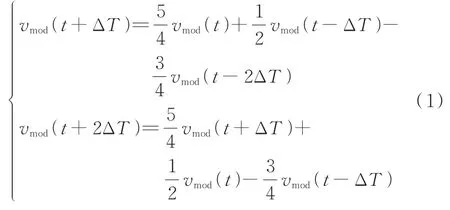
步骤4：结合预测结果vmod（t+ΔT）和vmod（t+2ΔT），利用拉格朗日插值法对t+ΔT到t+2ΔT时刻之间每个小步长时刻下控制系统的输出量进行预测，即

式中：ti为t+ΔT到t+2ΔT时刻之间的小步长时刻，ti=t+ΔT+nΔt，n=0，1，…，δ-1；lk（ti）为ti时刻插值节点k对应插值基函数的值；tλ为插值区间的终点t+2ΔT；K为插值节点的个数。

步骤5：根据步骤4 的结果计算t+ΔT到t+2ΔT时刻的开关状态，并于t+ΔT时刻向小步长侧传递。

与此同时，小步长侧在t时刻接收大步长侧于t-ΔT到t时刻计算出的t到t+ΔT时刻的开关状态，并以此为依据对t到t+ΔT时刻的电气状态进行求解，实现与大步长侧控制系统的并行计算。

将以上方法用于变流器控制系统与电气系统进行多速率解耦并行计算的实时仿真场景。考虑到控制系统的计算步长远大于电气状态求解，因此，改进插值算法增加的计算量不会对仿真系统的实时性产生明显负担。

2 基于FPGA 的硬件加速实时仿真实现

在大规模系统中，全部采用微秒级小步长进行电磁暂态仿真的效率是难以接受的［16］。因此，基于前文所介绍的改进插值算法，本文将电磁暂态仿真模型划分到不同的计算单元中，利用FPGA 并行性更强的优势处理小步长电气状态求解，使用基于CPU 的上位机处理规模更大、逻辑更复杂的大步长仿真计算，通过PCIe 总线完成不同步长仿真之间的数据交互，实现基于FPGA 的硬件加速实时仿真。具体结构见附录A 图A1。

仿真系统的计算时序及FPGA 部分的主要计算过程见附录A 图A2。本文采用文献［17］中的算法实现电磁暂态仿真。考虑到开关不同运行状态下导纳矩阵的变化将产生巨大的运算负担［18-19］，对于状态高频率变化的开关元件采用基于交叉初始化的变流器参数化恒导纳模型［20］进行建模求解。该模型下系统导纳矩阵恒定不变，可以将变流器导纳矩阵及相应逆矩阵在初始化过程中提前计算并存储。大步长开始时刻，上位机首先通过PCIe 总线发送上一步长下计算得到的接口状态、控制参数等信息到FPGA 端，然后，启动本时刻的变流器控制系统计算。与此同时，FPGA 端的电气状态求解过程主要包括以下步骤：

步骤1：在初始化阶段，利用导纳矩阵不随开关状态改变的特性分块预存变流器模型导纳矩阵及相应的逆矩阵。

步骤2：读取控制系统前一步长计算得到的各开关状态及接口状态。

步骤3：结合开关状态对各支路历史电流源在t时刻的电流Ihis（t）进行计算。

式中：Geq为支路等效电导；ubr(t-Δt)和ibr(t-Δt)分别为t-Δt时刻支路两端的电压和流过支路的电流；对于电阻、电感、电容等状态固定的支路，α、β均为定值［21］，对于开关支路，α、β的值取决于本时刻的开关状态［20］。

步骤4：根据系统电源以及各历史电流源的值计算t时刻各节点的注入电流，例如对于节点i及其相邻节点的集合w（i），有

步骤5：计算并更新各节点电压、各支路电流等电气状态量。

式中：U（t）和Iinj（t）分别为t时刻各节点电压和注入电流组成的向量；Y为系统导纳矩阵。

步骤6：更新仿真时间，若未达到结束时刻则重复步骤2—步骤6；若达到则将计算结果存储到指定地址等待上位机读取。

在与以上过程并行的大步长结束前，上位机将读取变流器电气状态的计算结果，完成基于FPGA的硬件加速实时仿真计算。

3 仿真分析

3.1 仿真精度分析

基于以上仿真方法，本文搭建了基于FPGA 的变流器硬件加速实时仿真系统。其中，CPU 端处理器型号为Intel Core i7-4770，核心数为8，主频为3.40 GHz；FPGA 芯 片 型 号 为Kintex Ultrascale XCKU060，采用PCIe3.0 接口与CPU 端上位机进行连接。同时，建立图3 所示的变流器模型作为算例，设CPU 端控制系统求解步长为100 μs，FPGA 端电气状态求解步长为1 μs，控制系统采用恒功率控制，电气及控制参数如表1 所示。图中：S1—S6为变流器开关元件；uabc、udq和iabc、idq分别为dq变换前、后的变流器交流侧电压和电流；Udc为变流器直流侧电压；f和θ分别为交流侧电压频率和相位；Pgrid和Qgrid分别为变流器输出的有功和无功功率；Pref和Qref分别为恒功率控制的有功和无功功率参考值。

表1 变流器算例参数设置Table 1 Parameter setting of converter example

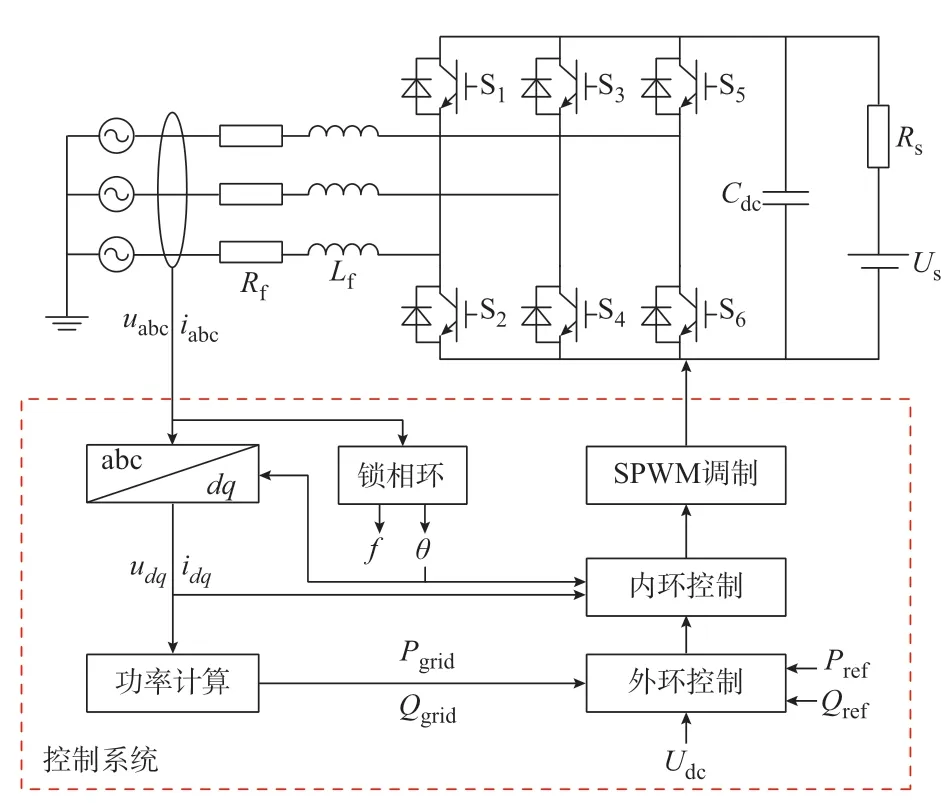
图3 三相桥式变流器算例系统示意图Fig.3 Schematic diagram of example system of three-phase bridge-type converter

3.1.1 仿真结果

为了验证本文所提出仿真方法的有效性，分别采用基于改进插值法的多速率并行时序（EP-ON）、无插值预测的多速率并行时序（EP-OFF）以及单一速率并行时序（SP），在以下2 种场景下对仿真平台进行测试，并在采用单一速率串行时序计算的离线仿真平台PSCAD 中搭建等效模型进行步长为1 μs的仿真作为对照。

1）场 景A：Pref和Qref分 别 为50 kW 和0 kvar，5.5 s 时交流侧BC 两相发生接地短路故障，0.1 s 后故障消除，得到仿真结果如图4 所示。

2）场景B：控制系统Pref初始设定为50 kW，Qref初始设定为0 kvar。5 s 时Pref突变为10 kW，Qref突变为20 kvar，得到仿真结果如图5 所示。

图4、图5 分别反映了在发生短路故障与控制参数变化的情况下，不同仿真计算方法所得到系统暂态过程的对比情况。图中，P、Q和Ia和Udc分别代表变流器交流侧输出的有功功率、无功功率A 相交流电流和直流侧电压；EP-ON、EP-OFF 和SP 分别代表改进插值方法和无插值方法下的多速率并行仿真和单一速率并行仿真结果。表2 给出了几种算法相对于离线仿真结果中变流器输出有功功率Pout和A相交流电流IacA的均方根误差，其中分别以发生故障或参数调整时刻前后0.2 s 内的仿真结果为样本，反映稳态及暂态情况下几种算法的误差大小。可以看出，采用单一速率并行时序得到的仿真结果与PSCAD 得到的结果极为接近，证明了本文所采用仿真模型的准确性。在稳态情况下，几种算法得到的仿真结果基本一致，但系统参数调整或发生故障后，无插值预测的多速率并行仿真结果与PSCAD离线仿真结果相比出现了一定偏差，而采用改进插值法的多速率并行仿真得到的结果与离线仿真结果基本一致，保持了较高的仿真精度，验证了本文所提出算法对于降低计算时序由单一速率串行转变为多速率并行时所产生时序误差的有效性。

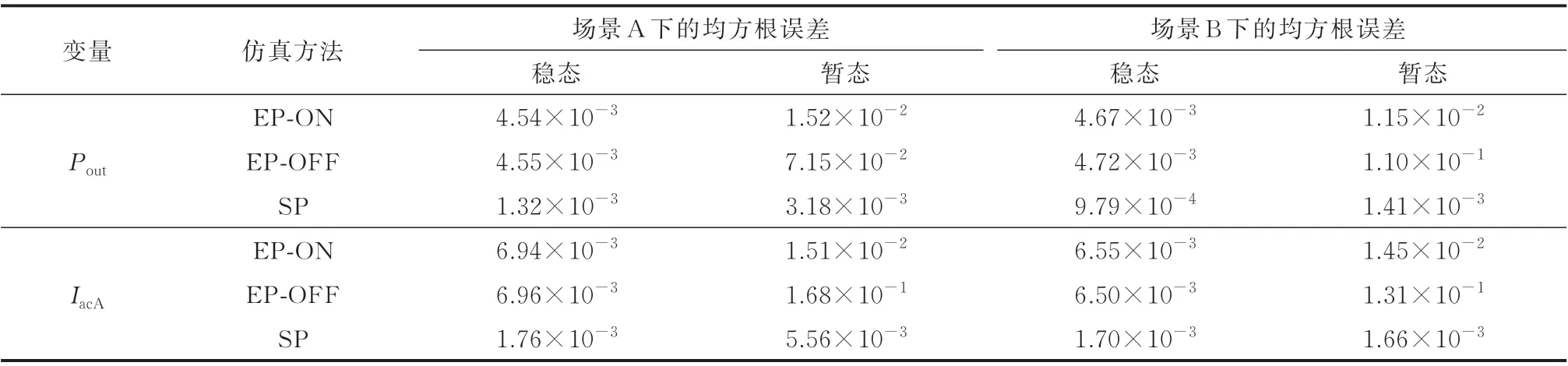
表2 不同算法的均方根误差对比Table 2 Comparison of root mean square errors of different methods

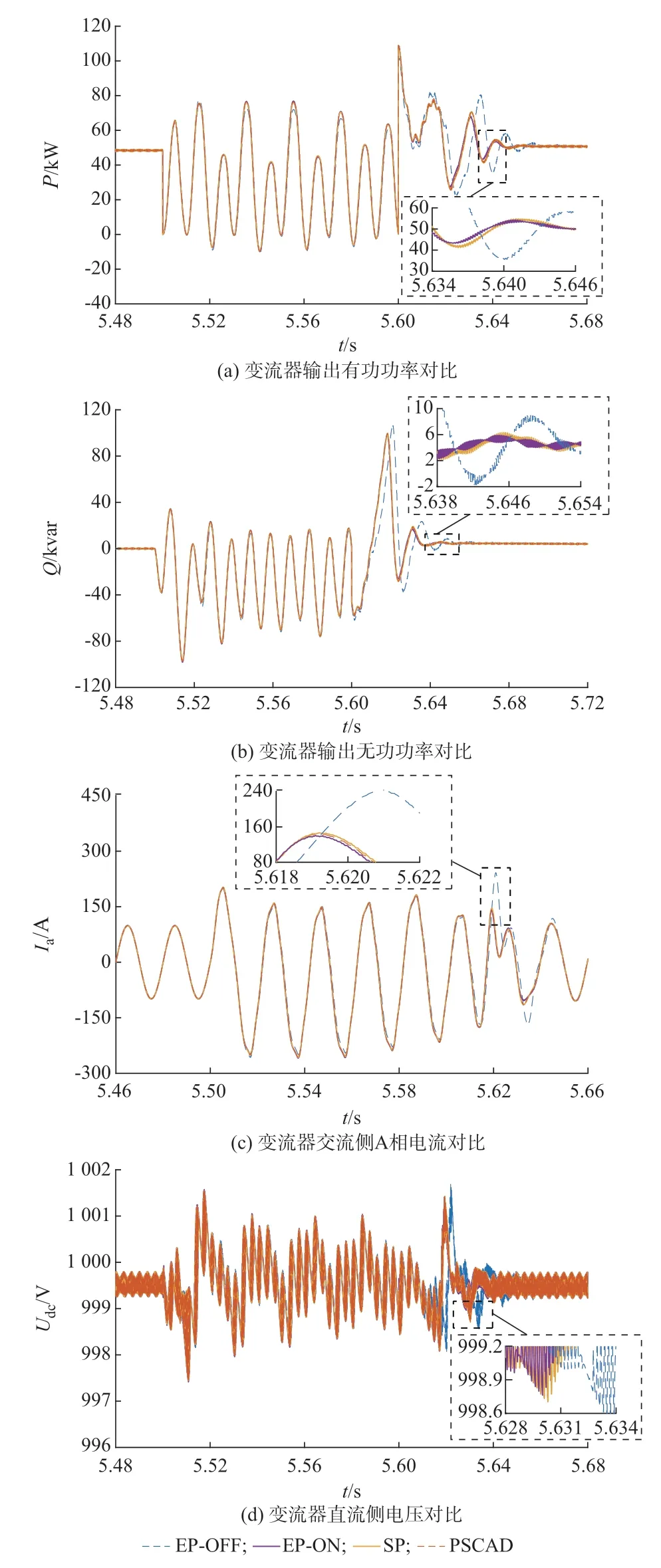
图4 场景A 下的仿真波形对比Fig.4 Comparison of simulation waveforms in scenario A

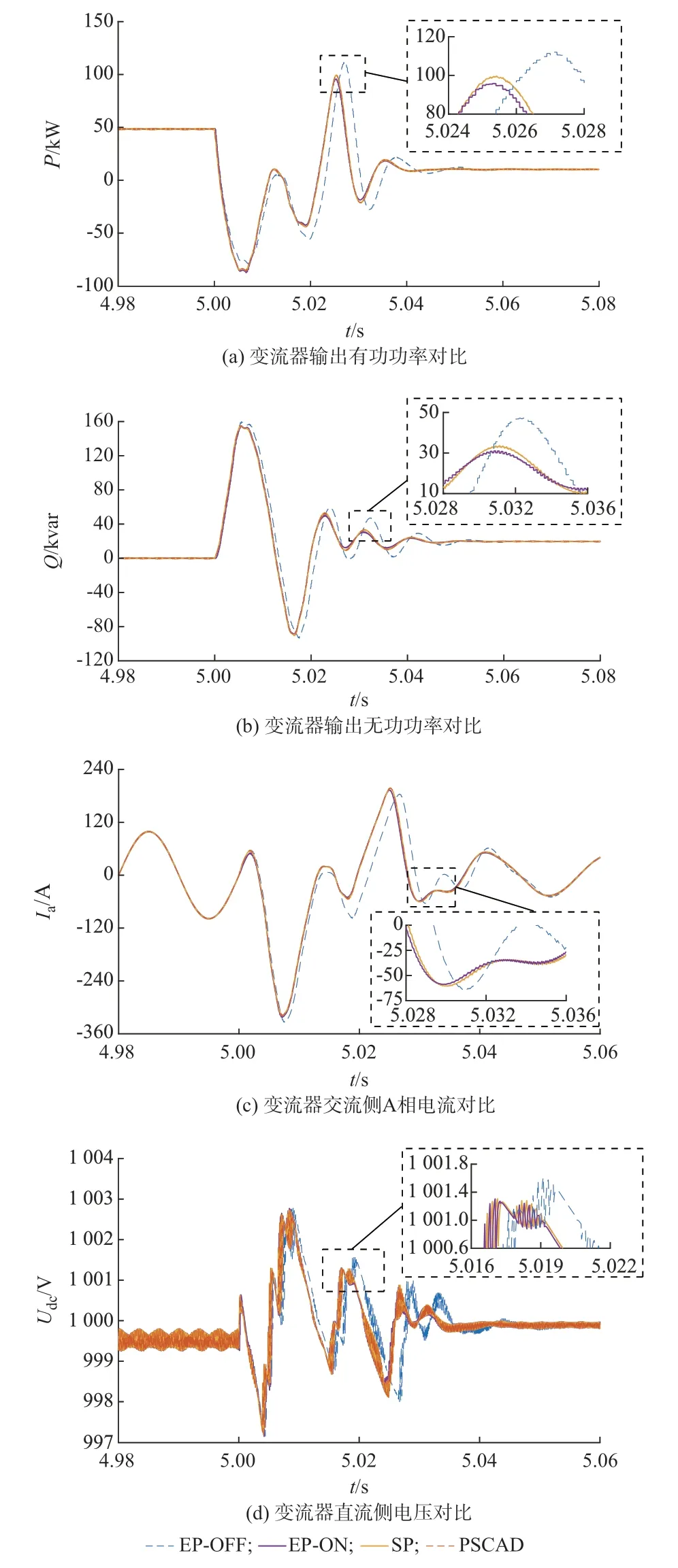
图5 场景B 下的仿真波形对比Fig.5 Comparison of simulation waveforms in scenario B

3.1.2 步长变化影响分析

本文所提出的改进插值算法用于降低多速率实时仿真场景下计算时序转变产生的时序误差，仿真步长的变化将对算法效果产生一定的影响。当仿真步长扩大时，场景A 下变流器交流侧输出电流的有效值相对于PSCAD 离线仿真结果的相对误差如附录B 图B1 所示。其中，SE 代表文献［14］所提出外插方法下的计算结果；设步长倍率δ固定为50，电气状态求解步长分别为1、2、3 μs。可以看出，在稳态条件下采用插值算法与无插值预测得到的仿真结果较为接近，但故障发生后的暂态过程中，无插值算法的多速率并行仿真时序下计算误差随步长的增加快速上升，而采用插值算法后误差的增长得到明显抑制，且本文所提出的改进插值算法对于计算精度的改善效果更好，验证了本文所提出仿真方法的有效性。

当电气状态求解步长固定时，时序变化引起的误差随步长倍率δ的增加而上升，而步长倍率取决于仿真场景的实际需求。在电力电子化程度较高的仿真场景下，可以采用微秒甚至纳秒级的仿真步长反映开关的高频特性，而配电网采用微秒或毫秒级的步长模拟［22］，需要根据网络模型的动态特性合理选择步长倍率。以场景B 为例，讨论δ变化对于本文所提出仿真方法的影响。设电气状态求解步长为3 μs，步长倍率δ分别为20、50 和100 时变流器交流侧B 相输出电流Ib与PSCAD 离线仿真结果的对比见附录B 图B2。可以看出，控制参数Pref与Qref调整前的稳态情况下，无论是否采用插值算法得到的结果都与离线仿真接近，但参数调整后的暂态过程中，无插值算法的多速率并行计算产生明显误差，误差收敛的速度与δ负相关。与文献［14］中的方法相比，改进插值算法对该误差表现出更好的抑制效果，使计算精度得到了显著改善。

3.2 计算性能与硬件资源消耗分析

实时仿真要求在每个步长下，仿真计算消耗的总时间低于仿真步长。在本文所建立的仿真平台上，上位机向FPGA 写入控制信息的平均耗时为10.391 μs，从FPGA 读 取 电 气 状 态 的 平 均 耗 时 为10.446 μs，数据传输的总时间为20.837 μs。由于控制系统与电气状态并行求解且控制系统的求解次数远小于电气状态求解，制约仿真平台实时性能的主要因素在于FPGA 侧的求解速度。以上算例中，FPGA 计算模块时钟频率为142.8 MHz，变流器电气状态求解过程中每个环节的计算耗时如表3 所示。其中，100 次小步长计算的总耗时47.747 μs 与数据传输的总时间20.837 μs 之和为68.584 μs，小于控制系统计算步长100 μs 且仍有充足裕度，有实现更大规模实时仿真计算的条件。在本文提出的硬件加速仿真方法中，CPU 端无须承担变流器电气状态求解任务，且解耦后的控制系统的求解次数相比串行时序显著减少，大大降低了CPU 端的仿真计算负担，提高了系统的实时仿真能力。

表3 仿真实时性能分析Table 3 Analysis on real-time simulation performance

在计算不变的情况下，高并行度计算通常需要占用更多的硬件资源。表4 所示为本文提出的硬件加速仿真结构与FPGA 独立实现仿真时，核心计算模块的主要硬件资源消耗情况对比。

表4 硬件资源消耗分析Table 4 Analysis on hardware resource consumption

表4 中，FPGA-S 表示FPGA 独立以单一速率并行时序实现仿真时的资源消耗；COSIM 表示在本文建立的硬件加速仿真平台中FPGA 的资源消耗情况。与本文所述硬件加速结构相比，FPGA 独立实现仿真时需计算控制系统输出，增加了并行程度较低、乘加运算较多的计算流程，故DSP48E 的消耗上升显著。与FPGA 独立实现的电磁暂态仿真相比，本文提出的硬件加速计算结构在保持高计算精度的情况下，有效降低了FPGA 的硬件资源消耗。

4 结语

本文提出了一种通过控制系统解耦实现多速率仿真的变流器电磁暂态实时仿真方法，分析了控制系统解耦计算过程中的时序和误差问题，采用一种结合拉格朗日插值的改进线性插值算法进行误差补偿，有效提高了控制器多速率解耦仿真的计算精度，并以该算法为依据搭建了利用FPGA 实现硬件加速计算的实时化仿真平台。将CPU 端与FPGA 端仿真步长分别设为100 μs 与1 μs，搭建采用功率控制的逆变器模型在系统故障和控制参数调整的场景下，分别与无插值算法的多速率仿真和PSCAD 离线仿真的结果进行对比。

仿真结果表明，本文提出的改进线性插值算法在精度上优于无插值算法的控制器多速率解耦仿真，更接近离线仿真得到的计算结果。此外，通过仿真计算耗时和硬件资源消耗情况分析，验证了本文所提出的变流器电磁暂态硬件加速实时仿真方法在保持高计算精度和实时性能的前提下，实现了更少的硬件资源消耗，具有良好的可行性和有效性。后续研究考虑建立种类更丰富的电磁暂态模型，实现多类型器件的大规模仿真。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。