基于D 分割法的LCC-HVDC 系统控制器参数整定方法

傅 闯，叶运铭，汪娟娟，周盛宇，李 欢，黄松强

（1. 直流输电技术国家重点实验室（中国南方电网科学研究院有限责任公司），广东省 广州市 510663；2. 华南理工大学电力学院，广东省 广州市 510641；3. 中国南方电网有限责任公司，广东省 广州市 510623）

0 引言

为了满足中西部清洁能源送出及东南部负荷中心电力供应的需求，中国大力发展高压直流输电技术［1-2］。截至2020 年底，中国已有近40 回直流工程投运，交直流混联电网的规模日趋庞大、运行特性日趋复杂。基于电网换相换流器的高压直流输电（LCC-HVDC）系统因其具有输送距离远、输电容量大等优势而得到了蓬勃发展［3］，但其存在换相失败及振荡发散等问题［4-5］。在一次系统结构参数及系统控制策略确定的前提下，控制器的比例-积分（PI）参数对系统性能有重要影响［6］。因此，对控制器PI参数进行整定优化，有利于保证交直流混联输电系统具有良好的稳定性及动态响应特性。

目前，已有学者对交直流混联输电系统控制器PI 参数的整定及优化方法开展了大量研究。文献［7-8］提出一种系统化的控制参数可行域划分优化方法，该方法能够综合考虑控制参数对系统稳定性及动态响应性能的影响，整定出的结果可认为是全局最优解。文献［9］提出一套多端混合直流输电系统控制器参数优化方法，可实现建立模型、计算控制参数可行域及对控制参数进行优化设计等功能。然而上述文献在获取控制器参数可行域时采用的是遍历法，计算工作量较大。文献［10］提出一种基于灵敏度分析的PI 参数优化方法，该方法在每次迭代时都要重新识别阻尼最小的临界模态，并重新计算对临界模态最敏感的控制参数。文献［11］采用模最优法及对称最优法分别对柔性直流输电系统的内环及外环控制PI 参数进行了整定。文献［12］以能够定量衡量系统小干扰稳定性的二次型指标为目标函数，采用蒙特卡洛方法对LCC-HVDC 系统的关键控制参数进行了优化。文献［13-18］均以智能优化算法为核心，针对不同目标函数对高压直流输电系统的控制器PI 参数进行了优化。然而，采用智能优化算法存在着整定结果可能陷入局部最优解的风险，整定结果的准确性高度依赖于算法的可靠性。已有文献大多只针对单一工况下系统的参数进行整定，当系统工况发生变化时，整定出的结果可能并不适用于新的工况。目前，在实际高压直流输电工程当中，常采用离线电磁暂态仿真和控制保护系统联调实验的方法整定控制器PI 参数，亟待进一步研究具有较强理论依据的系统性整定方法。

D 分割法在极平面与控制器参数空间之间建立了直接关联，通过将极平面稳定域的边界映射到参数空间，构造了参数空间中的D 分割边界，从而能够快速地确定控制器参数的稳定区域［19］。文献［20］提出将D 分割法应用于并网逆变器的PI 参数整定，对本文工作有相当大的启发。

综上，本文以单极全压运行方式下的LCCHVDC 系统为研究对象，提出一种基于D 分割法的多工况（10%～110%额定功率传输水平）通用控制器参数整定方法。本文所研究系统整流侧采用定电流控制策略，逆变侧采用定电压控制策略。首先，建立该系统的等值小干扰动态模型，并获得定电流及定电压控制回路的传递函数；然后，采用D 分割法获得控制器PI 参数的稳定域，并基于期望的控制回路稳定裕度及带宽对控制器PI 参数进行整定；接下来，将不同功率传输水平下的PI 参数整定域进行叠加，获得不同工况通用的PI 参数域；最后，在PSCAD 电磁暂态模型中对基于D 分割法获得的稳定域及整定后的控制器参数域进行了仿真测试，验证本文所提控制器参数整定方法的有效性。

1 LCC-HVDC 系统结构

本文所研究LCC-HVDC 系统的主电路及控制结构如图1 所示。图1 中：下标“r”代表整流侧相关变量，下标“i”代表逆变侧相关变量；Vs为交流电网的电压幅值；Rs和Ls分别为交流电网的等值电阻和等值电感；is为交流电网注入交流母线的电流；Vpcc为公共连接点电压幅值；FAC为交流滤波器组；ic为流经换流变压器网侧的电流；k为换流变压器的变比；Lec为换流变压器对直流侧的等效影响电感；Lm为换流站出口处的平波电抗器；Idc为直流电流；FDC为 直 流 滤 波 器 组；vr，d、vr，q和vi，d、vi，q分 别 为 整 流 侧 和逆变侧公共连接点电压的d、q轴分量；PLL 为锁相环；θ为锁相环的输出相位；Idc，ref和Udc，ref分别为直流电流和直流电压的指令值；αord和βord分别为整流阀和逆变阀的触发角指令值；αact和βact分别为整流阀和逆变阀的实际触发角。

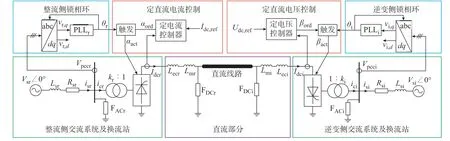
图1 系统主电路及控制结构Fig.1 Main circuit and control structure of system

2 LCC-HVDC 系统小干扰动态模型

某实际工程在单极全压运行方式下的额定直流电压为500 kV，额定直流电流为3 kA，额定输送功率为1 500 MW，直流输电线路长度为1 200 km。下面以单极全压满功率工况为例建立该系统的等值小干扰动态模型，其中换流站、定电流控制器、定电压控制器及锁相环的小干扰动态模型可参考文献［21-23］，本文不再赘述。系统运行及控制参数详见附录A 表A1 及表A2。

1）滤波器组模型。单极全压满功率运行时，整流侧交流滤波器组的投切策略包括：（1）3 组A 型（DT11/13）+2 组B 型（DT3/24/36）；（2）2 组A型+3 组B 型；（3）2 组A 型+2 组B 型+1 组C 型（Shunt C）。本文采用第（3）种投切策略对该工况进行建模，整流侧交流滤波器参数详见附录A 表A3。将相同的交流滤波器组支路进行并联等效后，可得整流侧交流滤波器组的等效结构如图2（a）所示，其中R1r～R3r、L1r～L6r及C1r～C6r分别为整流侧交流滤波器组相应支路的等值电阻、电感及电容。

考虑到需将交流母线处的dq轴电压作为状态变量，故在交流滤波器组中额外增添一条纯电容支路，该支路电容Cpccr取值为0.001 μF，此时其对交流电流及换流站无功功率的影响可忽略不计。根据图2（a）可得整流侧交流滤波器组d轴分量的小干扰动态模型为：

图2 等效结构图Fig.2 Equivalent structure diagram

式中：Δ 表示扰动量，下同；MA=diag［Cpccr，C1r，L1r，C2r，L2r，C3r，L3r，C4r，L4r，C5r，L5r，C6r，L6r］；M1=［vr，d，vC1r，d，iL1r，d，vC2r，d，iL2r，d，vC3r，d，iL3r，d，vC4r，d，iL4r，d，vC5r，d，iL5r，d，vC6r，d，iL6r，d］T，其中各电压及电流量均为相应电容电压及电感电流的d轴分量；M2=［，ωr］T，其中ωr为 整 流 侧 锁 相 环 的 输 出 角 频 率；M3=［vr，q，vC1r，q，iL1r，q，vC2r，q，iL2r，q，vC3r，q，iL3r，q，vC4r，q，iL4r，q，vC5r，q，iL5r，q，vC6r，q，iL6r，q］T，其中各电压及电流量均为相应电容电压及电感电流的q轴分量；M4=［Δisr，d-Δicr，d，0，0，0，0，0，0，0，0，0，0，0，0］T，其中isr，d和icr，d分别为整流侧交流电网注入交流母线的电流和流经换流变压器网侧的电流的d轴分量；MB1～MB4的表达式详见附录A 式（A1）—式（A4）。

整流侧交流滤波器组q轴分量的小干扰动态模型与式（1）类似。

逆变侧交流滤波器组在单极全压满功率运行时的投切策略包括：（1）5 组A 型（DT12/14）；（2）4 组A 型+1 组C 型。本文采用第（2）种投切策略对逆变侧交流滤波器组进行建模，其结构与参数详见图2（b）及 附录A 表A3，其中：R1i、L1i～L3i及C1i～C3i分别为逆变侧交流滤波器组相应支路的电阻、电感及电容；Cpcci为额外增添的纯电容支路电容，取值为0.001 μF。直流滤波器组的结构及参数详见图2（c）及附录A 表A3，其中Ld1r～Ld3r和Cd1r～Cd3r分别为直流滤波器相应支路的等值电感和电容。由于逆变侧交流滤波器组及直流滤波器组的建模思路同上述整流侧交流滤波器组类似，故本文不再赘述。

2）直流部分模型。本文采用集总等效电路中的π 型电路对直流输电线路进行模拟。由于直流输电线路单位长度的电阻通常远小于单位长度的感抗，因此可将直流输电线路归结为低损耗传输线。此时，根据文献［24-25］，为了对长度为l的低损耗传输线的特性进行物理模拟，集总等效电路中π 型电路的级联数目N应当满足：

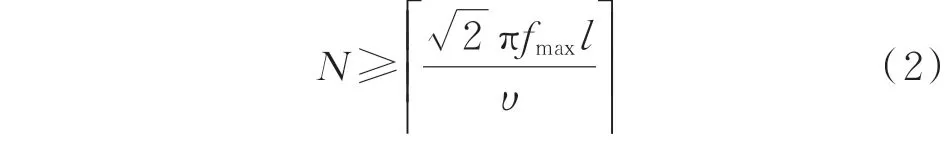
由于LCC-HVDC 系统在小干扰失稳的情况下其振荡频率一般小于100 Hz，且控制参数对系统阻抗特性的影响主要集中在小于200 Hz 的低频段，故本文将fmax设置为200 Hz。根据式（2），当对1 200 km的输电线路进行物理模拟时，需要级联的π 型电路数目最小为4。为了使系统的小干扰动态模型阶数不致过高，本文采用4 个π 级联电路来模拟直流输电线路。此时，系统直流部分的等效结构如图2（d）所示，其中：Udcr和Idcr分别为整流站出口处的直流电压 和 电 流；ULine1～ULine5及ILine1～ILine4为 状 态 变 量；RLine、LLine及CLine分 别 为 单 个π 型 电 路 的 电 阻、电 感及电容；Udci和Idci分别为逆变站出口处的直流电压和电流。根据图2（d）可得直流部分的小干扰动态模型如式（3）所示。

式 中：MF=diag［Lecr+Lmr，CLine，LLine，2CLine，LLine，2CLine，LLine，2CLine，LLine，CLine，Leci+Lmi］；M5=［Idcr，ULine1，ILine1，ULine2，ILine2，ULine3，ILine3，ULine4，ILine4，ULine5，Idci］T；MG和M6的 表 达 式 详 见 附 录A 式（A5）和式（A6）。

综上，当以定电流及定电压控制器指令值Idc，ref及Udc，ref为输入，以直流电流及直流电压测量值Idcr，m及Udci，m为输出时，本文所研究系统的小干扰动态模型可表示为：

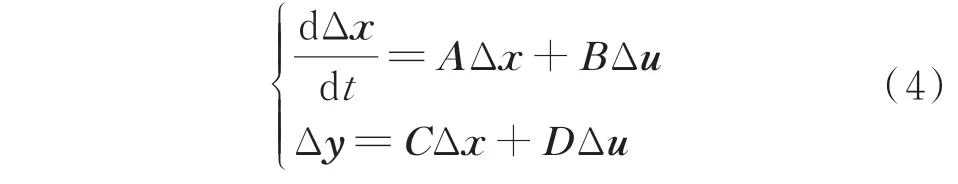
式中：x为状态变量；u为输入变量；y为输出变量；A为75×75 的状态矩阵；B为75×2 的输入矩阵；C为2×75 的输出矩阵；D为2×2 的前馈矩阵。

为验证上述小干扰动态模型的正确性，令控制器指令值发生扰动，得到单极全压满功率运行方式下PSCAD 电磁暂态模型与MATLAB 小干扰动态模型的系统动态响应，如附录A 图A1 所示。由图A1 可知，2 种模型的系统响应基本一致，表明了本文所建立的小干扰动态模型能够准确地反映系统的动态特性。

3 基于D 分割法的控制器PI 参数整定

3.1 D 分割法原理

含PI 控制器的单位负反馈控制系统如图3（a）所示，其中：s为复变量；R（s）为输入量；Y（s）为输出量；GPI（s）和G0（s）分别为开环传递函数中PI 环节和调制环节的传递函数，其表达式如式（5）所示。

图3 控制回路信号流Fig.3 Signal flow of control loop

式中：Kp和Ki分别为PI 控制器的比例和积分系数；a0，a1，…，an和b0，b1，…，bm分别为G0（s）分母和分子多项式的系数。

则该单位负反馈控制系统的闭环特征方程可表示为：

式中：K={Kp，Ki}为控制参数集合。

根据D 分割法可得控制器参数稳定域的边界为：

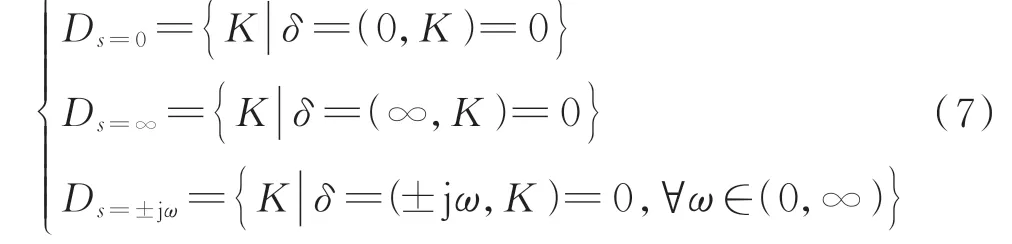
式中：Ds=0和Ds=∞为奇异边界；Ds=±jω为非奇异边界；ω为系统角频率。

将s=0 及s=∞代入式（6）可得奇异边界等价为：

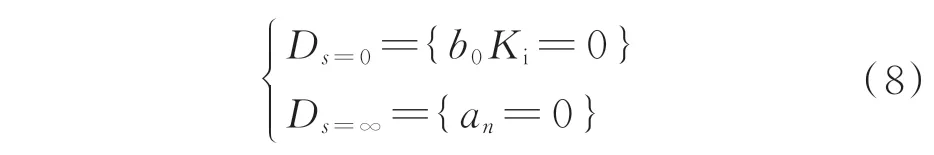
根据式（8）可知，由于an=0 不包含PI 控制器参数信息，因此Ds=∞不构成控制器参数稳定域边界的约束。而当b0=0 时，Ds=0也不构成控制器参数域稳定边界的约束，只有当Ki=0 时，约束关系才成立。因此得到一条奇异边界为：

对于非奇异边界Ds=±jω，为便于说明，不妨将G0(s)的频率响应写作G0（jω）=a（ω）+jb（ω）的形式，其中，a（ω）和b（ω）分别为G0（jω）的实部和虚部。此时令闭环特征方程等于0，可得：

求解式（10）可得：

综上，D 分割边界由式（9）及式（11）共同构成。

3.2 定电流控制器PI 参数整定

首先，对定电流控制器的PI 参数进行整定。为了得到类似图3（a）所示单位负反馈形式下的定电流控制回路，将式（4）进行拉普拉斯变换可得系统的多输入、多输出传递函数模型为：

式中：I为单位矩阵；GI-I（s）、GI-U（s）、GU-I（s）和GU-U（s）均为传递函数。

根据文献［19］，当仅考虑定电流控制回路的输入扰动时，可将定电压控制器指令值扰动量ΔUdc，ref置零，此时多输入、多输出系统可简化为单输入、单输出系统，定电流控制回路的信号流如图3（b）所示，其中：GPI，I（s）和GI0（s）分别为定电流控制回路开环传递函数中PI 环节和调制环节的传递函数，其表达式如式（13）所示。

式中：Kp，Idc和Ki，Idc分别为定电流控制器的比例和积分系数。

结合式（11）可得定电流控制器PI 参数的D 分割非奇异边界为：

式中：Re[·]代表取复数的实部；Im [·]代表取复数的虚部。

令ω在（0，+∞）内变化，则由式（14）可得其D分割边界曲线如图4（a）所示，图中阴影部分即为定电流控制器PI 参数的稳定域。

需要指出的是，由式（14）得到的D 分割边界曲线对应定电流控制回路处于临界稳定状态，当定电流控制器PI 参数组合（Kp，Idc，Ki，Idc）取为图4（a）中阴影部分对应的参数组合时，定电流控制回路是闭环稳定的，否则闭环失稳。而对于一个控制系统，一般要求其留有一定的增益裕度（gain margin，GM）和相位裕度（phase margin，PM），因此还需进一步整定图4（a）所示的控制器参数稳定域。将增益-相位裕度测试器［26］引入定电流控制回路中，能够方便地获得满足期望增益裕度及相位裕度的D 分割边界，如图3（c）所示，其中：h为期望增益裕度对应的放大倍数；φ为期望相位裕度对应的角度。

此时定电流控制器PI 参数的D 分割非奇异边界为：

基于自动控制原理，令定电流控制回路期望的增 益 裕 度MG，I和 相 位 裕 度MP，I满 足MG，I＞6 dB 且30°＜MP，I＜60°的要求，则在定电流控制器PI 参数稳定域内按照式（15）分别对MG，I=6 dB、MP，I=30°及MP，I=60°时的D 分割边界进行求解，得到各D 分割边界曲线及满足上述稳定裕度要求的定电流控制器PI 参数域如图4（b）所示。

当（Kp，Idc，Ki，Idc）取为图4（b）中阴影部分对应的参数组合时，能够保证定电流控制回路是闭环稳定的，同时该控制回路的稳定裕度满足MG，I＞6 dB 且30°＜MP，I＜60°的要求。

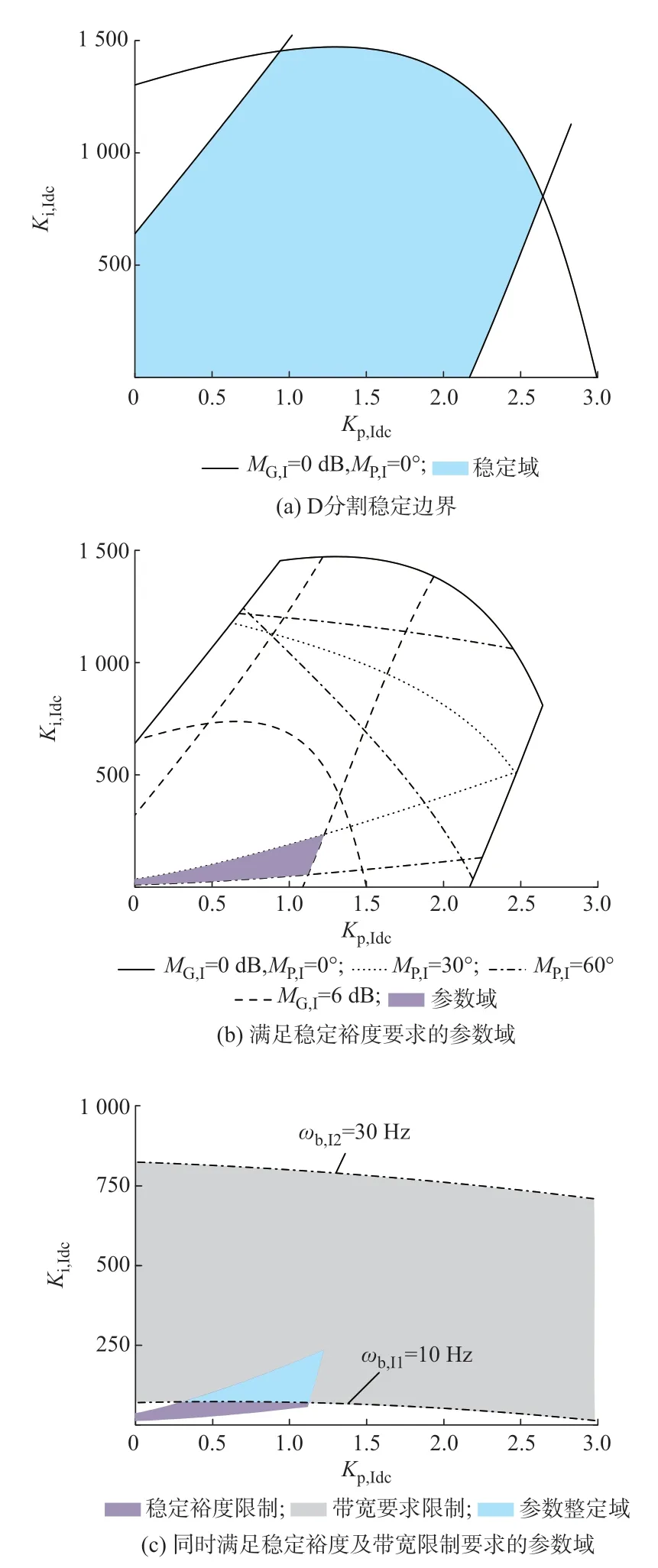
图4 定电流控制器PI 参数的D 分割边界及参数整定域Fig.4 D-partition boundary and parameter setting domain of PI parameter for constant current controller

下面推导定电流控制器PI 参数与定电流控制回路带宽ωb，I间的关系。当对ωb，I加以限制时，稳态下GI0（jωb，I）为一个可通过计算确定的复数，不妨令GI0（jωb，I）=AI+jBI，其中AI和BI分别为GI0（jωb，I）的实部和虚部，则根据带宽的定义有：

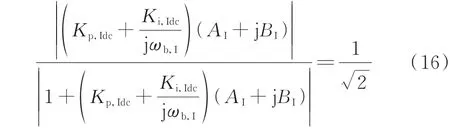
对上式进行推导可得：

考虑到LCC-HVDC 系统定电流控制环节的带宽通常处于10～30 Hz 范围内［27］，因此本文设期望的定电流控制回路带宽下限为ωb，I1=10 Hz、带宽上限为ωb，I2=30 Hz，令Kp，Idc在（0，3）范围内变化，根据式（18）计算出对应的Ki，Idc，求得满足带宽限制要求的定电流控制器PI 参数域，如图4（c）灰色阴影部分所示。将该参数域与图4（b）中的紫色阴影部分进行叠加，即可得到同时满足稳定裕度要求及带宽限制要求的定电流控制器PI 参数整定域如图4（c）蓝色阴影部分所示。

3.3 定电压控制器PI 参数整定

下面对定电压控制器的PI 参数进行整定。同3.2 节类似，当仅考虑定电压控制回路的输入扰动时，可将定电流控制器指令值扰动量ΔIdc，ref置零，此时可得定电压控制回路的信号流如图5 所示，其中：GPI，U（s）和GU0（s）分别为定电压控制回路开环传递函数中PI 环节及调制环节的传递函数，其表达式如式（19）所示。

图5 定电压控制回路信号流Fig.5 Signal flow of constant voltage control loop

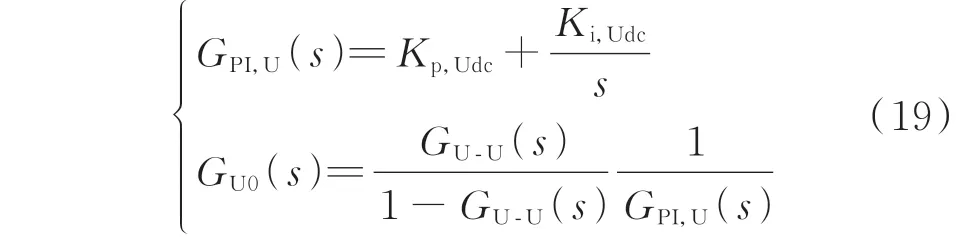
式中：Kp，Udc和Ki，Udc分别为定电压控制器的比例和积分系数。

结合式（11）可求得定电压控制器PI 参数的D分割非奇异边界为：

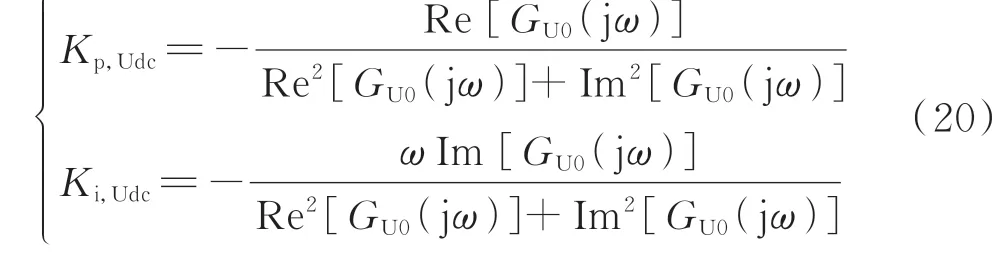
令ω在（0，+∞）范围内变化，则由式（20）可得其D 分割边界曲线如图6（a）所示，图中阴影部分即为定电压控制器PI 参数的稳定域。

图6 定电压控制器PI 参数的D 分割边界及参数整定域Fig.6 D-partition boundary and parameter setting domain of PI parameter of constant voltage controller

同样对定电压控制回路引入增益-相位裕度测试器，此时定电压控制器PI 参数的D 分割非奇异边界为：

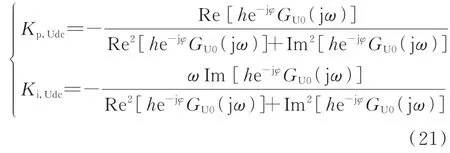
对于定电压控制回路，不妨令其期望的增益裕度MG，U和 相 位 裕 度MP，U满 足MG，U＞6 dB、60°＜MP，U＜80°的要求，则在定电压控制器PI 参数稳定域内 按 照 式（21）分 别 对MG，U=6 dB、MP，U=60°及MP，U=80°时的D 分割边界进行求解，得到各D 分割边界曲线及满足上述稳定裕度要求的定电压控制器PI 参数域如图6（b）所示。

当 定 电 压 控 制 器PI 参 数 组 合（Kp，Udc，Ki，Udc）取图6（b）中阴影部分对应的参数组合时，能够保证定电压控制回路是闭环稳定的，同时满足MG，U＞6 dB且60°＜MP，U＜80°的稳定裕度要求。

当对定电压控制回路的带宽ωb，U加以限制时，稳态下GU0（jωb，U）同样为一个可通过计算确定的复数，不妨令GU0（jωb，U）=AU+jBU，其中AU和BU分别为GU0（jωb，U）的实部和虚部，则采用类似3.2 节的推导过程可得Kp，Udc、Ki，Udc与ωb，U之间的关系为：

考虑到直流电压的调节响应速度较直流电流的响应速度慢，故本文设定电压控制回路的带宽下限为ωb，U1=5 Hz、带宽上限为ωb，U2=15 Hz，令Kp，Udc在（0，5）范围内变化，根据式（22）计算出对应的Ki，Udc，求得满足带宽限制要求的定电压控制器PI 参数域如图6（c）中灰色阴影部分所示。将该参数域与图6（b）中的阴影部分进行叠加，即可得到同时满足稳定裕度要求及带宽限制要求的定电压控制器PI参数整定域，如图6（c）蓝色阴影部分所示。

3.4 不同工况通用的PI 参数域

需要指出的是，上述理论模型的建立及参数整定的结果是以研究对象的额定功率传输水平Pd，e工况为例进行的，对于非额定工况，为了平衡无功功率水平以及维持交流母线电压值在合理范围内，需要对交流滤波器的投切进行适当配置。下面给出本文所研究系统在10%～110%额定功率传输水平下的交流滤波器配置方案，如表1 所示。

根据表1 可知，不同工况下换流站交流滤波器的配置方案可归结为如下3 种：

表1 不同工况下的换流站交流滤波器配置方案Table 1 AC filter configuration scheme of converter station under different operation conditions

1）整流站投入A、B、C 型交流滤波器，逆变站投入A、C 型交流滤波器；

2）整流站投入A、B 型交流滤波器，逆变站投入A、C 型交流滤波器；

3）整流站投入A、B 型交流滤波器，逆变站投入A 型交流滤波器。

由于C 型交流滤波器包含一个电感及一个电容元件，其投切会使得系统的小干扰动态模型阶数变化4 阶。因此，表1 中不同工况下系统对应的小干扰动态模型也可归结为3 种，如表2 所示。

表2 不同工况下系统对应的小干扰动态模型Table 2 Small-signal dynamic model of system under different operation conditions

对各个工况求取相应的小干扰动态模型，按照3.2 节及3.3 节的方法求取满足稳定裕度要求及带宽限制要求的控制器参数域，并将各个工况下获得的控制器参数域进行叠加，即可获得不同工况通用的控制器PI 参数域。本文求得的定电流控制器及定电压控制器通用PI 参数域分别如图7（a）和（b）中蓝色阴影部分所示。

图7 不同工况通用的控制器PI 参数域Fig.7 General PI parameter domain of controller for different operation conditions

4 仿真验证

本章在PSCAD 电磁暂态模型中对上述理论分析的结果进行仿真验证。以定电压控制回路为例，首先验证图6（a）所示由D 分割法获得的定电压控制器PI 参数稳定域边界的正确性。如附录B图B1（a）所示选取仿真所用PI 参数组合，并在PSCAD 中令（Kp，Udc，Ki，Udc）按图B1（a）中3 种参数组合情况进行阶跃：

Case1：令（Kp，Udc，Ki，Udc）在t=4 s 时 由 初 始 参 数阶跃至（2，2 400），0.18 s 后由（2，2 400）阶跃至（2，2 100）。

Case2：令（Kp，Udc，Ki，Udc）在t=4 s 时 由 初 始 参 数阶跃至（3，2 150），2 s后由（3，2 150）阶跃至（3，1 900）。

Case3：令（Kp，Udc，Ki，Udc）在t=4 s 时 由 初 始 参 数阶跃至（4.7，500），2 s后由（4.7，500）阶跃至（4.3，500）。

各情况下Udci，m的仿真响应波形如图8（a）至（c）所示。根据图8 可知，当（Kp，Udc，Ki，Udc）由初始参数阶跃至定电压控制器PI 参数稳定域外时，PSCAD 中Udci，m的响应波形呈振荡发散趋势，系统失稳；而当（Kp，Udc，Ki，Udc）再阶跃回定电压控制器PI 参数稳定域内时，PSCAD 中Udci，m的响应波形恢复稳定，与理论分析结果一致。将上述致使系统小干扰失稳的定电压控制器PI 参数组合代入小干扰动态模型中，计算失稳模式的特征值及对应的振荡频率，所得结果如表3 所示。

图8 定电压控制器PI 参数稳定域仿真验证Fig.8 Simulation verification of PI parameter stability domain of constant voltage controller

表3 振荡频率理论计算值Table 3 Theoretical calculation value of oscillation frequency

对图8 失稳阶段的仿真波形进行快速傅里叶变换分析，所得结果如附录B 图B2（a）至（c）所示。结合图B2 及表3 可知，振荡频率的仿真值与理论值较为接近。

类似的，对80%Pd，e及10%Pd，e功率传输水平下的定电压控制器PI 参数稳定边界进行仿真验证，在PSCAD 中 令（Kp，Udc，Ki，Udc）按 附 录B 图B1（b）和（c）中的参数组合进行阶跃，得到相应Udci，m的仿真响应波形如附录B 图B3 和图B4 所示。根据图B1、图B3及图B4 可知，仿真结果与理论分析结果一致，进一步验证了控制器参数稳定边界的正确性。

下面验证图6（b）所示由D 分割法获得的定电压控制器PI 参数整定域的有效性。当系统运行在100%Pd，e功 率 传 输 水 平 下 时，在PSCAD 中 令（Kp，Udc，Ki，Udc）按 附 录B 图B5（a）中 的 参 数 组 合 进 行取值，并令定电压控制器指令值在t=4 s 时阶跃下降0.02 p.u.，得 到Udci，m的 仿 真 响 应 波 形 如 附 录B 图B6 所示。由图B6 可计算不同控制参数下系统阶跃响应的超调量σ和调节时间ts，结果如表4 所示。

表4 不同控制参数下系统阶跃响应的超调量和调节时间Table 4 Overshoot and adjustment time of system step response with different control parameters

根据高压直流系统阶跃响应的基本要求，为使系统具有良好的动态响应性能，系统阶跃响应的超调量不应超过整定值变化量的30%。根据图B6 及表4 可知，当（Kp，Udc，Ki，Udc）取（0.4，400）及（3.8，600）时，系统阶跃响应超调量大于30%，超调量过大，且经多次振荡才达到新的稳态值；当（Kp，Udc，Ki，Udc）取（1.6，20）时，系统处于过阻尼状态，阶跃响应调节时间为193.0 ms，调节时间较长；而当（Kp，Udc，Ki，Udc）取整定域内参数（1.2，100）时，系统阶跃响应超调量较小，调节时间较短，系统具有较好的动态响应性能，验证了图6（b）所示由D 分割法获得的定电压控制器PI 参数整定域的有效性。

最后，对图7（b）所示不同工况通用的定电压控制器PI 参数整定域的有效性进行仿真验证。如附录B 图B5（b）所示，选取仿真所用PI 参数组合，其中，（Kp，Udc，Ki，Udc）=（3.2，220）、（Kp，Udc，Ki，Udc）=（0.1，45）及（Kp，Udc，Ki，Udc）=（0.6，30）为通用PI 参数域外的参数组合，（Kp，Udc，Ki，Udc）=（1.2，100）为通用PI 参 数 域 内 的 参 数 组 合。选 取110%Pd，e、10%Pd，e这2 种 工 况，并 令Udc，ref在t=2 s 时 产 生 扰 动 量ΔUdc，ref=0.02 p.u.，得 到 不 同 参 数 组 合 下Udci，m阶 跃响应波形的变化量如图9 所示。

对图9 中的各阶跃响应波形计算超调量、调节时间及时间乘绝对误差积分（integral of time multipled by the absolute value of error，ITAE）值［28］，所得结果如表5 所示。

表5 不同参数及工况下系统阶跃响应的动态性能指标Table 5 Dynamic performance indices of system step response with different parameters and operation conditions

根据附录B 图B5（b）可知，当（Kp，Udc，Ki，Udc）分别取为（3.2，220）、（0.1，45）时，定电压控制回路在110%Pd，e工况下不满足稳定裕度及带宽的要求，而在10%Pd，e工况下满足稳定裕度及带宽的要求，因此理论上这2 组参数组合中10%Pd，e工况下Udci，m的阶跃响应较110%Pd，e工 况 性能更优。图9（a）仿真结 果 表 明，10%Pd，e工 况 下Udci，m阶 跃 响 应 的 动 态 性能指标较110%Pd，e工况均明显减少；图9（b）仿真结果 表 明，尽 管10%Pd，e工 况 下Udci，m阶 跃 响 应 的 调 节时间有所延长，但由于其超调量明显减少，故ITAE指标有所减小，整体动态性能更优，与理论分析结果一致。

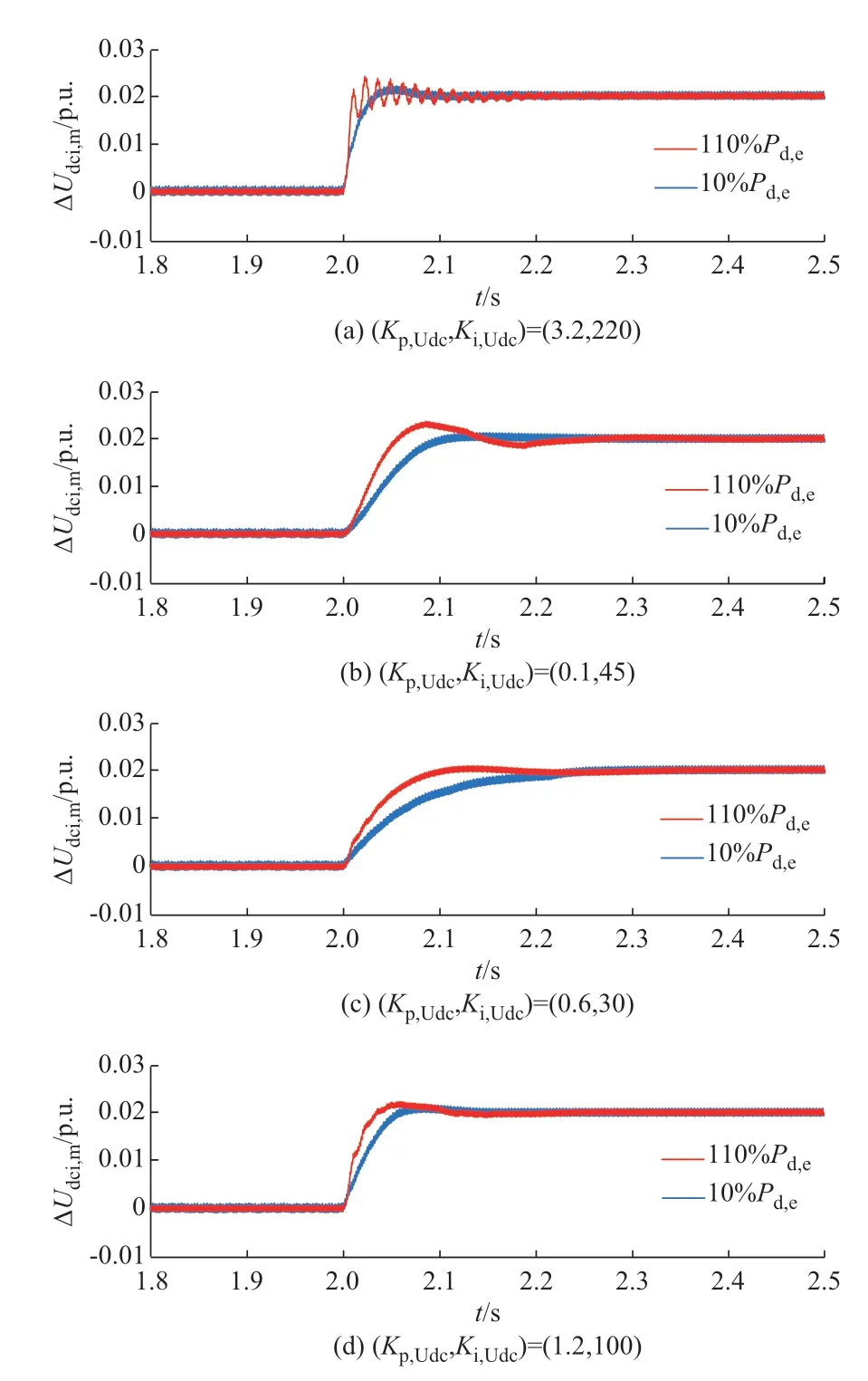
图9 定电压控制器通用PI 参数域仿真验证Fig.9 Simulation verification of general PI parameter domain of constant voltage controller

当（Kp，Udc，Ki，Udc）取为（0.6，30）时，定电压控制回路在110%Pd，e工况下满足稳定裕度及带宽的要求，而在10%Pd，e工况下不满足稳定裕度及带宽的要求，因此，理论上该参数组合下110%Pd，e工况Udci，m的阶跃响应较10%Pd，e工况性能更优。图9（c）仿 真 结 果 表 明，10%Pd，e工 况 下Udci，m阶 跃 响 应 的 调节时间较110%Pd，e工况延长了86.9 ms，使得ITAE指标明显升高，动态性能下降，与理论分析结果一致。

当（Kp，Udc，Ki，Udc）取为（1.2，100）时，定电压控制回路在110%Pd，e及10%Pd，e工况下均满足稳定裕度及带宽的要求。图9（d）仿真结果表明，110%Pd，e及10%Pd，e工况下Udci，m阶跃响应波形的动态性能差异不大，采用本文整定出的控制器通用PI 参数能够减小不同工况下动态性能的差异，验证了本文参数整定方法的有效性。

5 结语

本文基于某实际工程的运行参数建立了LCCHVDC 系统的等值小干扰动态模型，并基于D 分割法分别对定电流及定电压控制器的PI 参数进行了整定，获得了单极全压运行方式下不同功率传输水平通用的控制器PI 参数域。整定出的参数能够使得直流控制回路在10%～110%额定功率传输水平下均满足稳定裕度及带宽限制的要求。

需要指出的是，本文所研究系统整流侧及逆变侧间存在耦合，对其中一侧控制器参数进行整定时需固定系统其余控制参数，对多组控制器参数同时进行整定的方法有待进一步探索。此外，本文尚未进行系统动态模拟验证，接下来将在与实际工程参数的对比分析和工程应用方面展开进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。