基于数据驱动的家庭能量实时经济调控方法

王玉彬，董 伟，陈源奕，2，杨 强

（1. 浙江大学电气工程学院，浙江省 杭州市 310027；2. 浙江大学工程师学院，浙江省 杭州市 310058）

0 引言

以分布式电源（distributed generator，DG）为代表的清洁能源利用是实现能源转型和缓解全球气候变化问题的重要途径［1-2］。同时，用户基于家庭能量管 理 系 统（home energy management system，HEMS）通过需求响应（demand response，DR）可实现柔性可调资源的运行调控，以提升能源利用效率和经济性［3-4］。通常，家庭能量经济调控的目的是根据电价等动态信息，在满足用户需求和可控电器以及储能系统（energy storage system，ESS）的运行约束前提下，实现系统设备的优化控制从而节省运行成本。然而，由于家庭能量系统运行的不确定性，如DG 出力的不确定性、用户用能行为的随机性，以及实时电价动态变化等因素，能量最优经济调控面临着诸多技术挑战。

目前，HEMS 优化方法可主要分为2 类：

1）第1 类为基于动态规划和博弈论等理论的模型驱动方法。该类方法基于预测数据或者假设数据已知来构建优化模型实现家庭能量的优化管理，但由于存在不可避免的预测误差，基于模型驱动的优化调度方法会产生调度决策结果不准确的风险。例如，文献［5］采用预测值构建优化模型，并采用启发式算法对模型进行求解，以实现家庭能量的多时间尺度优化管理；文献［6］基于环境预测数据和预设的用能需求数据建立用电策略，实现电器的优化运行和智能用电；文献［7］假设用户各时段的用电负荷已知，构建了一种基于非合作Stackelberg 模型的家庭用户DR 策略，在供用电双方的效用优化方面取得了较好的效果。 基于模型预测控制（model predictive control，MPC）［8］的调度框架通过滚动预测可实现能量的实时优化管理，但仍会受到预测误差的影响。例如，文献［9］采用MPC 建立了一种多阶段的HEMS 策略，但由于预测误差的存在使得调度策略不为最优的情况时有出现。

2）第2 类为基于机器学习的数据驱动方法，其中，强化学习因其优秀的决策能力已成为家庭能量调控的常用数据驱动方法［10-11］。文献［12］采用分布式深度强化学习寻找电网与家庭用户之间非合作随机博弈的纳什均衡，从而降低了用户以及电网的运行成本；文献［13］提出一种基于异步深度强化学习的家庭能源系统的在线优化调度方法；文献［14］基于深度强化学习，提出了一种家庭综合需求响应的在线优化方法；文献［15］利用极限学习机对电价和光伏出力进行预测，基于强化学习获得电器和电动汽车的调度决策，以实现电费和用户不舒适度的最小化；文献［16］考虑了多类型负荷需求，结合深度强化学习和深度确定性策略梯度算法，提出了一种无模型的实时能量调控方法。但是，将强化学习应用于能量调控问题存在奖励函数设置复杂以及训练困难的问题。近年来，部分学者将模仿学习方法［17］应用于能量系统的调度决策中，其基本思想是通过对历史状态与其对应的最优决策数据进行学习，从而建立状态与动作之间的复杂映射关系，进而得到最优策略模型。该类方法可基于系统当前状态实时获取调度决策结果，从而避免了数据预测误差的负面影响，并且具有计算速度快和算力要求低的优点。例如，文献［18］提出了一种云-边协同架构下基于监督学习的孤岛微网实时能量调控方法；文献［19］针对气电耦合系统场景，基于大量历史经济调度模式，通过人工神经网络（artificial neural network，ANN）学习系统状态与经济决策间的复杂映射关系，实现了快速经济调度决策。

基于上述内容，本文基于模仿学习思想，针对家庭场景提出了一种基于监督学习的数据驱动能量实时经济调控方法。通过将系统实时运行状态作为决策模型输入，实现家庭用电器和ESS 的在线优化调度决策。通过仿真对所提出方法进行了验证，实验结果表明了方法的有效性和优越性。

1 基于数据驱动的HEMS 方法概述

1.1 家庭能量系统结构

本文所研究的家庭能量系统如图1 所示，由一个HEMS、不同类型的用电器、ESS 和屋顶光伏（photovoltaic，PV）发电单元组成。

图1 家庭能量系统结构示意图Fig.1 Schematic diagram of structure of household energy system

该系统通过智能电表与主电网相连接，通过PV 发电和外部电网获取电能以满足用电需求。HEMS 通过智能电表接收主电网发送的实时电价信息，以及PV 发电功率、用电器和ESS 状态等信息，并据此按照优化策略做出调度决策，下发至设备执行，达到提高整体能量效率和降低家庭用电成本的目的。本文中，家庭用电器根据其特性和优先级可分为不可控负荷和可控负荷2 类［20］。PV 发电单元的发电功率取决于光照强度等天气条件，不可调度。

1.2 HEMS 实时优化框架

本文所提出的基于模仿学习思想的家庭能量实时经济调控方法的整体思路为：基于历史场景的最优调度方案构建训练集，并通过神经网络模型学习当前系统运行状态与能量调度决策之间的映射关系，从而得到基于数据驱动的经济调度决策模型。在系统运行时，以当前系统的实时运行状态作为决策模型的输入，并计及家庭用电器和ESS 的运行约束，最终得出能量调度决策结果。具体如下：每个时段不同类型用电器的优化决策结果由各用电器当前所处的运行状态确定，家庭能量系统在t时段的状态st包括不可控负荷功率、实时电价、ESS 的荷电状态（state of charge，SOC）、PV 发电功率以及当前所处的调度时段。在t时段，HEMS 的优化调度决策目标at为各用电器的运行功率以及ESS 的充/放电功率，当各用电器和ESS 的运行决策确定以后，系统与电网的交换功率即可通过相应计算得到。

HEMS 优化决策的目标是根据当前时段系统的状态st决定相应的优化调度决策at。基于此，本文提出了一种基于数据驱动的家庭能量实时经济调控方法。通过监督学习方式，基于大量历史数据建立系统状态与优化决策之间的复杂映射关系，从而实现根据当前系统状态实时确定相应的优化调度决策。该方法以当前时段的实际状态信息作为输入，无须预测，避免了预测误差对调度决策的影响，克服了基于模型驱动的优化调度方法因预测误差导致调度决策不准确的风险，其整体路线如图2 所示。

图2 基于数据驱动的家庭能量实时经济调控方法框架Fig.2 Framework of data-driven real-time economic regulation method for household energy

首先，基于大量历史运行数据，通过求解工具Gurobi［21］离 线 求 解HEMS 数 学 模 型，得 到 各 用 电 器在每个优化周期内所有时段的优化调度决策；然后，采用调度决策对相应各时段的运行状态进行标注并构建训练数据集；之后，利用ANN 可以拟合输入与输出之间复杂非线性映射的能力，通过训练数据集学习得到系统状态与调度决策之间的关系，构建基于ANN 的优化调度决策模型。在新的运行状态到来时，将系统的实时运行状态输入训练完成的ANN模型中，并在ANN 的输出结果上施加各用电器和ESS 的约束得到最终的优化调度决策。其中，HEMS 的数学模型将在后续章节中进行详细描述，包括目标函数及相应运行约束。

在训练数据集的构建阶段，为了保证所提出调度决策模型在实际应用中的泛化性和有效性，可以充分利用场景生成技术［22-23］，通过积累的历史数据来模拟获取足量的运行场景用于数据集构建，使其尽可能囊括所有的系统运行情况。同时，在系统运行过程中出现未知场景和模式时，可以将其添加进数据集中，对模型进行增量学习和阶段性的重训练，从而实现调度决策模型的自学习和自趋优效果［18］。

2 HEMS 数学模型

2.1 不可控负荷

家庭能量系统中的不可控负荷是指对用户生活影响较大，根据用户需求在能量分配过程中必须即时满足的负荷，如电视机、电脑等用电器，其运行功率不可调节，并且不受HEMS 调度。该类负荷的大小会随着用户的用电需求和用电习惯实时波动，在HEMS 优化调度问题中，各时段不可控负荷的总功率需要根据历史数据通过预测得到。

2.2 可控负荷

可控负荷可以在最大和最小功率之间响应电价等信息的变化以可变功率灵活运行，如空调等用电器。其可以在电价较高时减小所消耗的功率从而节省电费，但减小运行功率会导致用户的不舒适度提升，从而产生不满意成本，该不满意成本可以通过二次 函 数 表 示［24］。用 电 器n在t时 段 的 效 用 函 数Un，t如式（1）所示。其中，等号右边第1 项表示用电成本，第2 项表示用户的不满意成本。

式中：t=1，2，…，T，表示当前的调度时段，其中T为一个调度周期内的调度时段总数；Δt为调度时段长度，本文选取时段长度为15 min，以实现高时间分辨率下的实时调控；λ(t)为t时段的电价；Pn(t)为用电器n在t时段的运行功率，且Pn(t)需满足式（2）和式（3）所示的运行约束；Pmaxn为用电器n允许的最大运行功率；αn为用电器n的不满意成本系数。αn可以由用户根据对用电器的依赖程度自主制定，其值越大，表示用户越倾向于消耗更多的电能来提高舒适度水平从而减小不满意成本，反之亦然。

用电器n的约束式（3）表示，用电器n只能在用户 所 定 义 的 可 运 行 时 间 范 围[tn，ini，tn，end]内 运 行，此时间范围外该用电器不会启动，运行功率为0。

2.3 ESS 模型

ESS 是一种可以实现负荷转移的可控负荷，ESS 通过在电价较低时充电、在电价较高时放电来减少向主电网的购电功率，从而达到节约用电成本的目的。ESS 的数学模型如下：

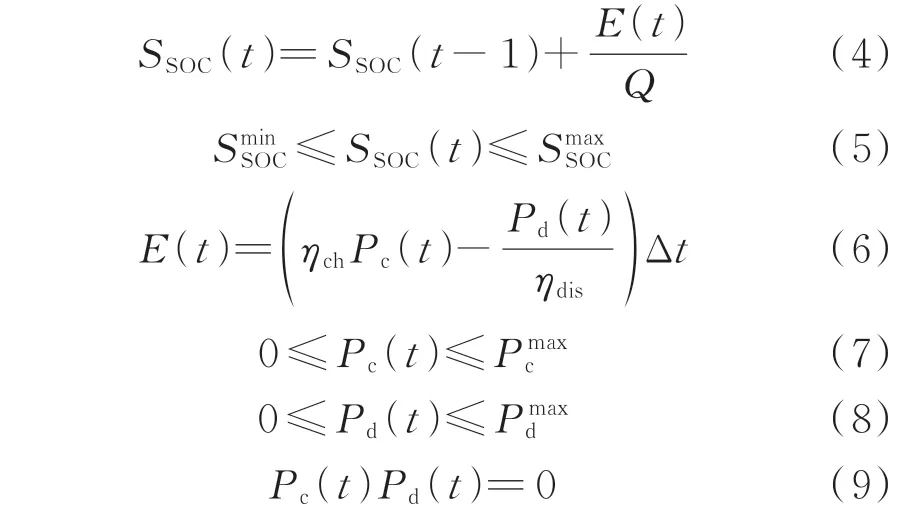
式中：SSOC(t)为ESS 在t时段的SOC，根据式（4）和式（6）进行计算；E(t)为ESS 在t时段储存的电量；和分别为ESS 的SOC 的下限和上限；ηch和ηdis分别为ESS 的充电和放电效率；Q为ESS 的额定容量；Pc(t)和Pd(t)分别为ESS 在t时段的充电和放电功率和分别为ESS 充电和放电功率的上限。约束式（5）用于对ESS 的SOC 进行限制，以避免ESS 的深度充放电影响其使用寿命；约束式（9）表示在同一时段ESS 不能同时充电和放电。

2.4 目标函数

HEMS 对用电器及ESS 的运行功率进行调控的目标在于最小化用户的用电成本和不满意成本。根据以上各类用电器的模型，用电成本的减少必然会导致用户针对该用电器的不满意成本增加，因此，需要在用电成本和不满意成本之间进行均衡。HEMS 的目标函数可构建如下：

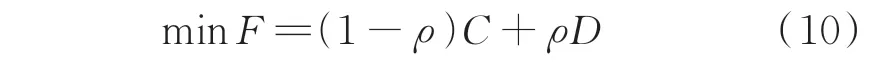
式中：F为总的目标函数值；C和D分别为从外部电网购买电能的用电成本和不满意成本；ρ为平衡参数，可以根据用户的偏好设置，用以实现用电成本与不满意成本之间的平衡［25］，其值越大表示用户越倾向于消耗更多的电能来提高舒适度，以减少不满意成本。

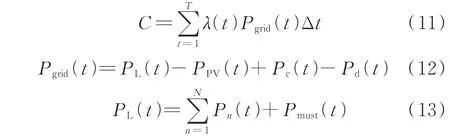
式中：Pgrid(t)为t时段与电网连接线的交换功率；PL(t)为t时段的负荷功率，其值等于可控负荷与不可控负荷的功率之和；Pmust(t)为t时段的不可控负荷功率；N为用电器总数量；PPV(t)为t时段的光伏输出功率。

总的不满意成本如式（14）所示，其等于所有用电器各时段的不满意成本之和。

基于模型驱动的HEMS 优化调度决策方法是根据预测得到或者假设已知的一个优化周期内的不可控负荷功率、实时电价及PV 发电功率等信息，在满足各用电器和ESS 约束的前提下求解目标函数，从而得到各用电器和ESS 在各时段的优化调度决策。

3 ANN 结构和工作机理

如前文所述，求解第2 章中的数学模型需要得知一个调度周期内所有时段的PV 发电功率、实时电价和不可控负荷功率信息。在日前无法掌握相关准确信息的情况下，需要通过预测方法预测得到，进而基于MPC 方法对各用电器进行优化调度。目前，已有较多关于预测方法的研究来提高预测精度，但精确预测仍是一个难以完成的任务。由于预测误差的存在，基于模型驱动的优化调度方法会产生调度决策结果不准确的风险。而本文提出的基于模仿学习思想的实时经济调控方法可将决策问题转换为监督学习，通过学习系统运行状态与调度决策之间的复杂映射关系来构建基于数据驱动的调度决策模型。基于训练完毕的模型，以系统当前实时状态信息作为输入，可实时实现系统调度决策。本文所采用的ANN 结构和具体原理阐述如下。

ANN 是由一层输入层、一层输出层和多层隐含层组成的全连接层网络。每一个神经元根据式（15）求取输入的加权与偏置常数的和，对该和值通过一个激活函数的处理后向下一层传递信息。

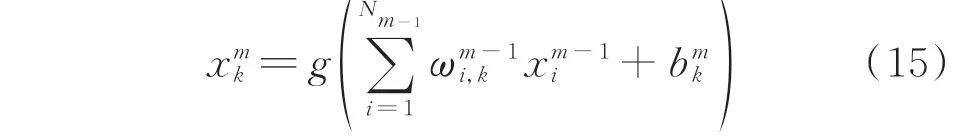
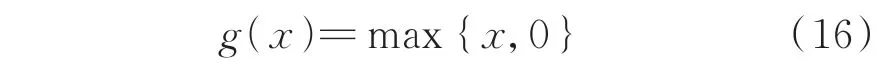
ANN 的训练过程如下：首先，随机生成权重以及偏置常数；然后，利用训练样本的输入-标签对，将样本输入经过前向传播过程产生估计输出，计算估计输出与样本真实输出值之间的误差，并通过误差的反向传播更新每个神经元的权重和偏置常数，直到误差收敛，完成ANN 的训练。训练结束后，ANN即可建立输入与输出之间复杂的非线性映射关系，在得到新的输入值时，输入训练完成的ANN 即可立即计算得到输出结果。

4 算例分析

4.1 仿真设置

本文采用图1 所示的家庭能量系统来评估本文所提出的基于数据驱动的家庭能量实时经济调控方法的性能。本文设置6 个可控负荷，包括3 台空调（AC1、AC2、AC3）、1 台热水器（H）、2 个灯具（L1、L2），以及必要的不可控负荷（额定功率设为3 kW）。为不失一般性，本文所提出的优化决策方法可以方便地扩展到更多用电器的场景中，在用电器数量减少时也可以很方便地修改模型以应用于相应场景中。

自然地，用户对不同的用电器可能具有不同的依赖程度（如书房或者卧室中的灯具，书房中需要灯具消耗更多的功率来提供更高的亮度）。用户可以根据对用电器的依赖程度设置式（1）中的不满意成本系数αn，对依赖程度高的用电器设置更大的αn，以消耗更多的电能减小不满意成本。各用电器的相关参数根据文献［26］设置，如表1 所示。ESS 参数设置如表2 所示，PV 发电单元的额定功率设置为3 kW。调度周期为1 d，时段长度设置为15 min。

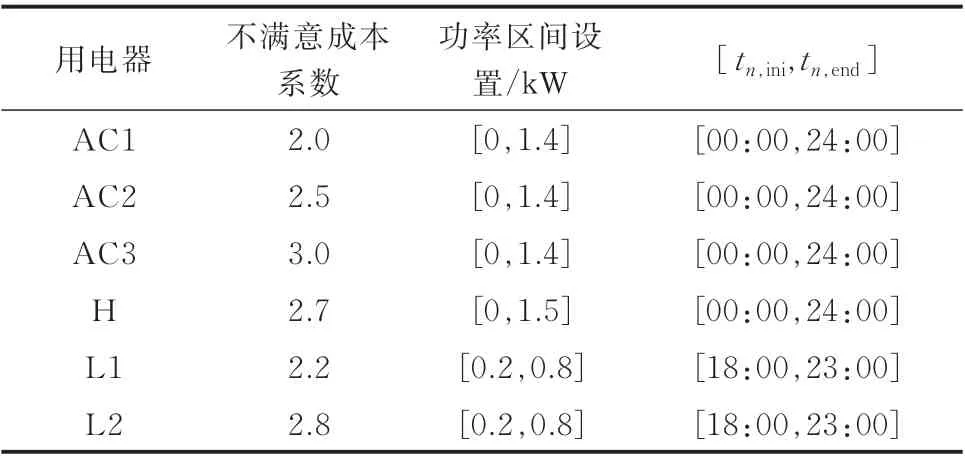
表1 各用电器的参数设置Table 1 Parameter setting of each electrical appliance

表2 ESS 参数设置Table 2 Parameter setting of ESS

在基于模型驱动构建数据集的过程中，采用Gurobi Python API 在Python 3.7 环境下建立模型并优化得到决策结果，然后，进行标注以构建训练数据集。在数据驱动部分，利用Pytorch 1.7.0 构建ANN，并进行训练得到基于ANN 的优化决策模型。仿真程序均在硬件配置为2.90 GHz Intel Core i5-9400U CPU 和8.00 GB RAM 的计算机平台上运行。

本文仿真数据来源如下：电价和负荷数据来源于澳大利亚新南威尔士地区的电力市场数据［27］，光伏出力数据根据该地区的光照数据转换得到［28］。选择2019 年1 月1 日—6 月30 日的数据构建训练数据集，对所提出的基于ANN 的优化调度决策模型进行训练，并以2019 年7 月1 日—7 月31 日的 数据作为验证集对ANN 进行测试。附录A 图A1 给出了历史数据分布，包括PV 发电功率、不可控负荷功率以及实时电价。从图中可以看出，每日历史数据在每个时段的PV 发电功率、不可控负荷功率以及实时电价的变化规律大致相同，如每天约在00：00—06：00 处于负荷的低谷期，07：00—09：30 负荷逐渐上升，并一直维持在较高的水平，PV 发电功率则在每日的12：00 左右达到出力高峰，实时电价的趋势则大致与不可控负荷功率趋势相同。

该规律表明，家庭能量系统每日运行模式存在较强的规律性，适合采用ANN 学习优化决策策略的内在规律，建立系统状态和优化决策之间复杂的映射关系，从而构建得到基于ANN 的优化决策模型。从图中也可以看出，训练数据包含范围较大，可令ANN 有充足的训练样本以保证模型的泛化性。

在本文基于ANN 的调度决策模型中，由于输入和输出的维度较小，建立深层ANN 易导致过拟合，因此，本文建立了一个具有2 层隐含层的浅层全连接ANN，用以学习并产生各用电器和ESS 的最优调度决策［19］。ANN 的输入为当前时段的系统状态，其为5 维向量，故输入层节点数设置为5。为了在有用电器增加时方便扩充本文所提出的优化调度决策模型，考虑为每一个用电器和ESS 单独构建一个ANN。然后，将构建完成的ANN 模型在HEMS上配置执行，其输出结果为该用电器和ESS 的优化决策，因此，每一个ANN 的输出层节点数设置为1。根据神经元数设置中3∶2 的经验规则［29］，设置不同ANN 结构进行测试，如附录A 表A1 所示，共设置4 个ANN 结构（包括1 个单隐含层网络）。其他ANN训练参数设置如下：mini-batch 设置为100，网络学习率为0.001，采用Adam 优化器对网络权重进行更新。

经过100 个epoch 训练后，AC1 运行功率的训练集和测试集的损失函数值下降过程如附录A 图A2所示。从图中可以看出，各网络结构训练集和测试集在经过数个epoch 的训练过程后，均可以很快收敛到较小的值，且趋势大致相同。这也表明，由于本文应用场景输入、输出维度不大，隐含层神经元个数和网络层数对ANN 性能影响较小。因此，本文选择神经元个数居中的Net2 结构。

4.2 结果讨论

为评估本文所提优化决策方案，首先，设置目标函数中的平衡参数ρ=0.5，基于模型驱动的优化决策方法利用历史数据得到训练数据集；然后，利用训练集训练基于数据驱动的优化决策模型。随机选取2019 年8 月2 日的数据，利用训练完成的模型在各时段求取各用电器和ESS 的优化决策。图3 展示了各用电器在各时段的运行功率。

由图3（a）可知，AC1、AC2 和AC3 的运行功率的整体变化趋势为：在电价升高时运行功率减小，在电价降低时运行功率增大。例如，在时段1～23 电价下降，3 台空调的运行功率上升，之后电价开始上涨、运行功率下降，时段27 电价上升到峰值，此时，3 台设备的运行功率也减小到最小值，然后电价开始下降，其运行功率也随之增加。在时段64～96，也有类似现象发生。该现象说明，本文所提方法能够有效追踪电价的变化，从而调节用电器的运行功率并节约用电成本。

图3 用电器在各运行时段的运行功率Fig.3 Operation power of electrical appliances during each time slot

图3（a）中展示的结果也可以说明不满意成本对用电器运行功率的影响。3 台空调的额定功率相同，但在整个决策周期内，AC3 的运行功率大于AC2，而AC2 的运行功率大于AC1，其原因是3 台空调的不满意成本系数αn的大小不同。AC3 的αn最大，意味着用户对AC3 的依赖程度最高，倾向于消耗更多的电能以降低不满意成本；相反，AC1 的αn最小，用户对其依赖程度相对较低，可消耗较少的电能。用户可以根据自己的需求调整不满意成本系数。

图3（b）和（c）展示了其他可控负荷H 和L1、L2在各时段的运行功率。从图中也可以明显看出，H和L1、L2 的运行功率随电价变化而变化。L1 和L2的运行功率在不可运行时段内的运行功率为0，在可运行阶段，电价上涨时运行功率下降、电价下降时运行功率增加。H 和L1、L2 的运行功率变化进一步说明，本文所提方法能够追踪电价变化并据此调节用电器的运行功率，以达到降低电费成本的目标。在整个运行周期内，L2 的运行功率一直高于L1，这也是由于L2 的不满意成本系数高于L1 而导致其运行功率较高。图3 所示的结果也表明，由于在ANN的输出结果上施加了相应的用电器约束，从而保证了用电器的运行功率不会越过运行约束。

为了进一步分析本文所提优化决策方法的有效性，图4 展示了各时段总负荷功率PL以及ESS 的充放电功率。为了展示清晰，当ESS 功率为负时表示充电、为正时表示放电。从图中可以看出，HEMS可以根据电价的变化协调ESS 的充放电行为，当电价较低时充电储存电能，电价较高时放电释放所储存的电能满足部分用电需求，以减少电价高峰时段向主电网的购电功率，从而起到降低用电成本的作用。ESS 在时段15～25 的电价相对较低，此时进行充电储存电能，在时段27～37 的电价高峰时段进行放电。同样地，在时段47～60 和73～85 也会有类似现象，在时段47～60 电价处于低谷时充电，在时段73～85 电价处于高峰时放电，以满足部分负荷的用电需求、减少购电成本。

图4 家庭能量系统决策结果Fig.4 Decision results of household energy system

图5 展示了调度周期内ESS 的SOC 变化曲线。可以看出，本文所提的优化调度方法可以根据电价的变化协调ESS 的充放电行为，从而达到节省用电成本的目的。在电价较低时段，ESS 通过充电储存电能，SOC 上升；在电价高峰时段释放电能，SOC 降低。如图5 所示，时段15～25 电价较低，在充电行为下SOC 迅速上升；从时段27 开始电价上涨，故ESS放电，SOC 下降。同时，由于在ANN 的输出结果上施加了ESS 设备约束，能保证ESS 的SOC 不会超过预先设定的［0.2，0.8］的范围，从而确保了ESS 的合理使用。

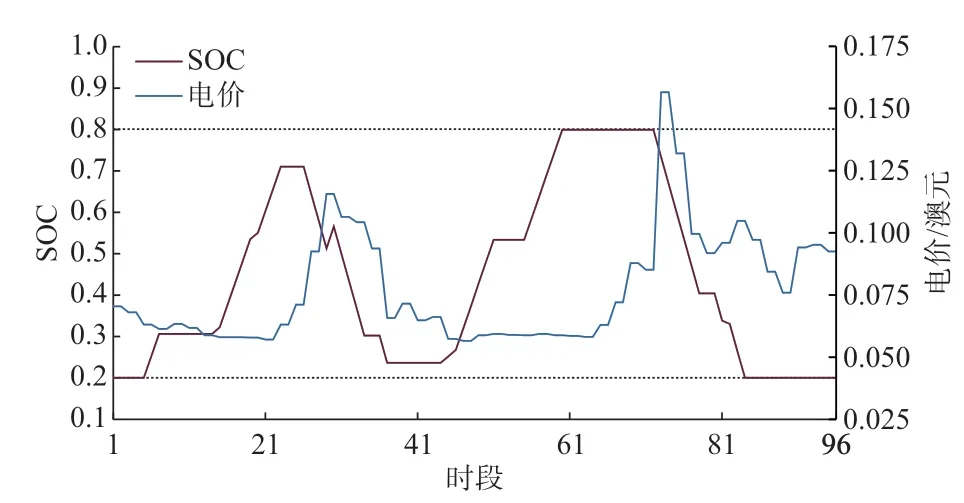
图5 ESS 的SOC 变化曲线Fig.5 SOC variation curve of ESS

为了进一步评估本文所提方法的性能，采用基于MPC 的调度方法作为基准方法与本文所提方法的经济性进行对比。MPC 方法利用预测信息通过HEMS 模型执行日前调度，得到调度结果。当预测信息的误差减小为0 时，可以获得在确定信息下的理想调度结果。然而，实际上不可能获得准确的预测信息，尤其是在高时间分辨率场景下（如15 min），其不可避免的预测误差必然会导致调度结果的不准确。而且在家庭能量系统中，用户随机性较大，预测更加不准确。本文在真实数据中加入均值为0 的高斯白噪声模拟预测数据，并考虑不同预测误差水平对所提方法的性能进行评价。所添加不同水平的高斯白噪声的方差参数如表3 所示。

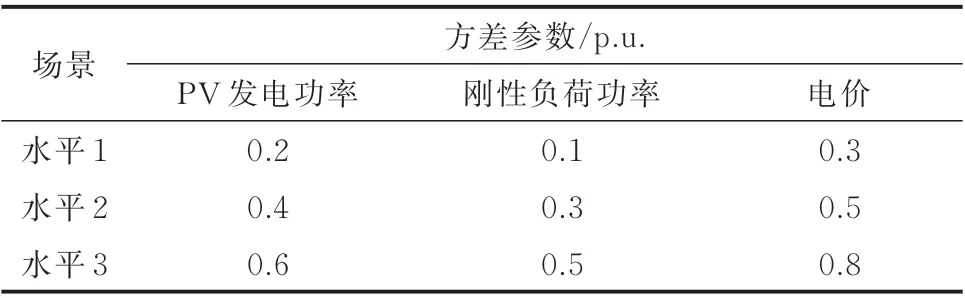
表3 预测误差方差参数Table 3 Variance parameters of forecast errors

表4 展示了2019 年8 月2 日各场景下的用电成本。可见，本文方法相比于MPC 方法，在运行成本方面获得了更好的性能，能够有效降低系统的运行成本。对应于3 种水平的预测误差，本文方法在用电成本上的性能分别提高了1.24%、2.34%、2.49%。由于源荷和电价的不确定性，采用MPC 方法时调度结果会受到预测准确度的影响，当预测信息误差很大时，将会给优化调度结果带来较大的风险，而本文方法则能够避免预测误差所带来的影响。

表4 不同调度方法的日运行成本Table 4 Daily operation cost with different regulation methods

图6 给出了无预测误差时3 台空调的理想调度决策结果。与图3（a）中展示的本文方法的调度结果相比，3 台空调的运行功率趋势基本一致，这也验证了本文方法的有效性和合理性。

图6 理想场景下3 台空调在各运行时段的运行功率Fig.6 Operation power of three ACs during each time slot in ideal scenario

为了对比平衡参数ρ对优化决策结果的影响，分别设置平衡参数ρ的值为0.8 和0.3 来重新构建训练数据集，训练构建本文所提基于数据驱动的家庭能量实时经济调控模型，并对测试日2019 年8 月2 日的运行状态进行实时优化决策，与前述ρ=0.5 时的决策结果进行对比。附录A 图A3 展示了AC1 在不同平衡参数ρ下各时段的运行功率。从图中可以看出，较大的ρ会导致更大的运行功率，这是由于更大的ρ会使得不满意成本所占的权重更大，用户倾向于消耗更多的电能以提高自身的舒适度水平，减小不满意成本。该结果进一步说明，本文所提出的基于数据驱动的家庭能量实时经济调控方法可以有效建立系统状态与用电器优化运行决策之间的复杂映射关系，从而对用电器的运行功率进行实时优化调度，在满足用户需求的前提下降低用户的用电成本。

通过上述实验结果分析可见，本文所提出的数据驱动方法可从历史场景数据集中高效学习系统运行状态与能量调度决策之间的映射关系与模式，在不同平衡参数下均可获得用电器和ESS 不同类型设备的合理决策结果。由于该方法不依赖于对系统运行状态的预测，可有效避免预测误差对系统能量调度的负面影响。

5 结语

本文提出了一种基于数据驱动的家庭能量实时经济调控方法。该方法利用历史运行数据通过模型驱动方式构建训练数据集，从而训练ANN 以构建基于数据驱动的调度决策模型，并且施加用电器和ESS约束保证设备运行不会超过约束限制。该方法的优点在于以实时运行数据作为输入，无须对不可控负荷功率、实时电价和PV 发电功率等数据进行预测，相比于基于模型驱动的MPC 调度方法，避免了预测误差对调度结果的影响。仿真结果表明，本文方法能够根据实时电价的变化对用电器运行功率和ESS 的充放电功率实时做出优化决策，降低了运行成本。

基于本文研究，得到主要结论如下：

1）基于模型驱动的优化调控方法会随着用电器的增多使得决策变量维度呈爆炸式增大，从而需要具有强大算力的求解模型，在家庭环境中显然难以具备这样的算力条件，这也阻碍了家庭需求响应的普及。

2）相比于基于模型驱动的优化调控方法，本文方法框架可以更为方便地扩展至更多的用电器场景中。可以基于云边协同的模式，在云端对模型进行训练，并将训练完成的模型下发至边缘设备执行，算力要求低。

3）本文所提出的方法具有良好的普适性，可以扩展和应用至含有多种不同能源和负荷类型耦合运行的城市区域综合能源系统中。

未来工作中，将研究把本文所提出的数据驱动模型架构应用于解决复杂综合能源系统的能量协调和优化调控问题中，同时，考虑将数据驱动方法与物理模型驱动方法相结合，使得模型具有更好的可解释性和泛化能力。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。