基于线损协方差分析的群体性固定比例窃电行为检测方法
2022-07-12张蓬鹤杨艺宁宋如楠彭彦林赵海森
薛 阳,张蓬鹤,杨艺宁,宋如楠,彭彦林,赵海森
(1. 中国电力科学研究院有限公司,北京市 100192;2. 国网重庆市电力公司,重庆市 400015;3. 新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
0 引言
电力系统中的窃电行为是用户通过一定的技术手段和工具,非法篡改电能表或者侵入量测系统,导致用电量或电费低于其实际使用量[1]。固定比例窃电指的是用户窃电量和总电量的比值是不随时间变化的常量,因此是一种线性的攻击方式。大多数篡改电能表硬件的窃电手法,如欠压法、欠流法,均表现为固定比例窃电[2]。虽然最近也出现了一些针对电网信息流的非线性窃电方式,但是这些高科技窃电所涉及的技术门槛较高,在窃电成本和普及范围等方面远不如固定比例窃电。而近年来,用户窃电行为呈现团体化、群体化的趋势。因此,群体性固定比例窃电是电网公司反窃电工作中所面临的最主要窃电方式。
当前的窃电检测方法大致可以分为3 类[3]:基于博弈论、基于用电行为模式和基于系统状态的方法。第1 类方法将窃电问题描述成窃电用户与电力供应商之间的博弈,通过分析正常和窃电用户在用电量分布上的差异,实现窃电检测[4]。该方法的主要问题在于建模难度较大。第2 类方法假设窃电用户的用电模式偏离正常用户的用电模式,通常采用分类和聚类等人工智能技术(例如基于支持向量机[5]、卷积神经网络[6]和其他神经网络法[7-8]等)来分析用电数据。这类方法需要大量可靠的训练样本,同时会受到样本污染[9]的影响。而聚类方法不需要带标签的训练样本,重点关注数据中的离群信息。文献[10]和文献[11]分别采用基于密度和噪声应用的空间聚类(density-based spatial clustering of applications with noise,DBSCAN)法和密度峰值快速搜索(clustering by fast search and find of density peaks,CFSFDP)法计算待检用户的异常度。聚类方法的问题是不擅长检测出固定比例的窃电用户。第3 类方法利用窃电行为会打破数据协同性[3]这一现象来检测窃电用户[12-13]。文献[14]和文献[15]利用三相状态估计来检测绕越用户。此类方法虽然能够检测固定比例的窃电用户,但是需要实时掌握配电网的精细拓扑及参数。
目前,针对固定比例窃电最有效的检测方法是基于相关性分析的方法。该方法采用数据集中器记录一个台区内所有用户的总用电量。文献[16]通过求解一组欠定线性方程来检测固定比例窃电用户。文献[17]采用最大信息系数(maximum information coefficient,MIC)检 测 与 非 技 术 性 损 失(nontechnical loss,NTL)相关性强的窃电用户。该方法擅长检测单个固定比例的窃电用户,在面对群体性的固定比例窃电时容易出现漏判。
为了克服上述方法的局限性,本文提出了一种基于线损协方差分析(line loss covariance,LLC)的窃电检测方法,主要工作为:1)建立了固定比例窃电用户电量和NTL 之间的数学模型,并发现了两者的相关性存着一种递增现象;2)把对群体性固定比例窃电的检测问题转化一个组合优化问题,并提出了求解该组合优化问题的寻优算法;3)利用中国某省电力公司提供的实测数据和窃电模拟实验平台生成的窃电数据进行了数值试验,结果表明LLC 方法对于群体性固定比例窃电场景具有较好的准确度和稳定性。
1 问题陈述与建模
1.1 场景描述
典型的10 kV 配电网结构如附录A 图A1 所示。其中,关口变压器同时向多个台区供电,每一个台区包含一组邻近的用户。本文提出的方法适用于安装了数据集中器的台区,得益于线路拓扑的稳定和集中器本身的安全,集中器记录的电量是台区内所有用户真实电量的累加。在这种情况下,台区的NTL就可直接由集中器记录的电量Wt减去全体用户的表计电量计算得出,表达式为:

式中:A为台区全体用户组成的集合;u~i,t为用户i在t时段的表计电量;Wt为t时段台区集中器记录的表计电量;ωt为台区t时段NTL。
对于没有安装数据集中器的台区,其NTL 可以通过文献[18]和文献[19]中的损耗估计算法间接求得。这种情形下,本文方法仍然适用。
现假设台区内存在若干窃电用户,记全体窃电用户组成的集合为C,其元素数量为m;同时记剩余正常用户的集合为B,其元素数量为n。本文重点探讨的问题是:当C只包含固定比例的窃电用户时,怎样准确检测出这些窃电用户。
1.2 NTL 与用户电量之间的数学模型
假设用户i∈C,且真实用电量为ui,t。如果用户i是一个固定比例的窃电用户,其攻击方式是线性的,表达式为:

式 中:αi为 用 户i的 表 计 电 量u~i,t与 真 实 电 量ui,t的 比值,且ai∈(0,1),它是一个不随时间变化的常量,取值与用户i具体实施的窃电手法有关。
而当C只包含固定比例的窃电用户时,由这群用户产生的NTL 为:
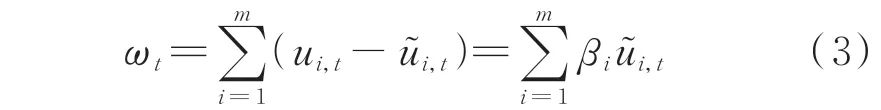
式中:i∈C;βi=1/αi-1,为窃电用户i电能表少记的电量与表计电量的比值。由于ai∈(0,1),故βi∈(0,+∞)。
把一天T个时间段的NTL 和用户表计电量向量化,得到对应的NTL 向量ω=[ω1,ω2,…,ωT]T和 表 计 电 量 向 量=[,,…,]T,由 式(3)可得:

上式表明,当C只包含固定比例的窃电用户时,台区的NTL 向量ω可以由这群窃电用户的表计向量线性表示,表示系数为βi。因此,可以认为ω与窃电用户|i∈C的相关性远大于其与正常用户′|i′∈B的 相关性,表达式为:

式中:F(·)为相关性函数。
当台区内只有单个固定比例窃电用户时,式(5)是严格成立的。但当台区内存在多个固定比例窃电用户时,由于NTL 向量是由这群窃电用户共同决定,可能导致某些情况下,式(5)不一定成立。以附录A 图A2 中包含4 个固定比例窃电用户的台区为例,这4 个窃电用户的电量曲线与台区的NTL 曲线在形态上并不相似。同时,附录A 表A1 的皮尔逊相关系数(Pearson correlation coefficient,PCC)也表明单个窃电用户的u~i与ω之间的线性相关性并不强。在这种情况下,如果仍然按照相关性的强弱来检测窃电用户,将出现严重漏判。

台区NTL 向量ω和组合向量u~C将具有很强的相关性。此外,附录A 表A1 的数据显示,窃电用户表计电量每叠加一次,叠加后的向量与ω的相关性也越来越强,即出现递增现象,如式(7)所示。
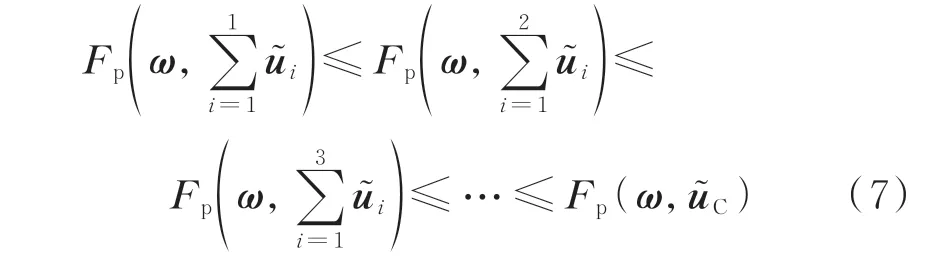
式中:Fp(·)为皮尔森相关性函数。
1.3 递增现象成立性分析
如果式(7)所示的递增现象不是个例,就可以用来检测群体性固定比例窃电用户。在利用上述递增现象来检测窃电用户之前,首先要分析其成立的前提条件。为了便于分析,需要将所有的向量按照下式进行标准化处理,得到标准化后的NTL 向量ω*和表计向量,表达式为:

式中:x*为标准化后的向量;x为标准化前的向量;xh为向量x的第h个的元素;max {xh}为x中最大元素的值。
标准化处理使得所有向量具有同一量纲,协方差的大小也能够衡量向量之间线性相关性的强弱[20]。因此,对式(7)成立性的分析可以转变成对式(9)的证明,表达式为:
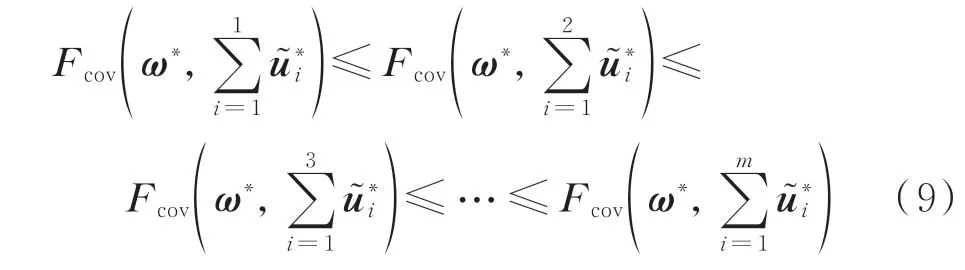
式中:Fcov(·)为协方差函数;上标*表示标准化后的向量。
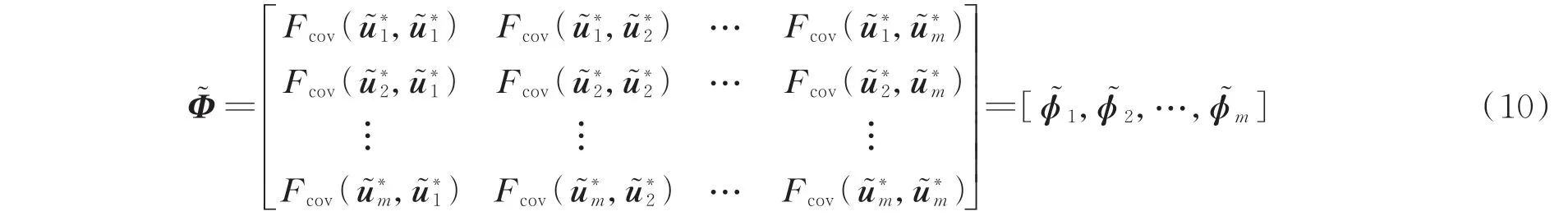


综上,如果任意2 个固定比例窃电用户的表计电量正相关,随着窃电用户表计电量逐渐叠加,它们与NTL 的相关性也越来越强。尽管满足这种递增现象是需要一定条件,但从工程实用角度出发,依据这一现象进行窃电检测是可行的。
2 检测方法及框架
2.1 检测方法
根据1.3 节的分析,当式(15)的条件满足时,固定比例窃电用户具有递增性,但这种递增性并不是固定比例窃电用户所独有的。为了准确检测出C,还需要另一个关于固定比例窃电用户特性的有用信息。
记用户集合A中任意一个具有1.3 节所述递增性质的子集为P*,即存在着一种排序,使得P*中的用户按照这种顺序依次叠加,叠加后的表计向量与NTL 向量ω*的相关性越来越强。为了便于表示,将集合P*全体用户的表计向量叠加起来得到的组合向量记为,即:

显然,当式(15)条件满足时,集合C也是一个P*。由于ω*与窃电用户的满足线性方程(11),可以认为窃电用户集合CR中的窃电用户电量全部叠加后与ω*的协方差Fcov(ω*,)近似为所有P*中Fcov(ω*,)的最大值,表达式为:

基于式(17),可以把对C的检测问题转化为下述优化问题:从所有具有上述递增性的用户集合P*中,找到使得Fcov(ω*,)最大的集合,具体表达式如式(18)所示。

当式(15)的条件满足时,问题(18)的解P*max就近似为C。

4)终止条件:在k阶寻优后,如果k=m+n-1,说明寻优过程已经遍历完所有用户,寻优终止;或者,在k阶寻优后,在进行k+1 寻优时,如果不存在k+1 阶递增路径,说明协方差已不再增加,寻优终止。

2.2 实用化问题
在应用过程中,上述方法还需要考虑2 个实际问题。
第1 个问题是检测耗时。LLC 方法耗时主要取决于2 个因素:待检用户数量,即集合A的大小;以及子问题最优解搜寻过程中,对应的搜寻终止阶数。由于待检用户总数是无法控制的,为了提高LLC 方法在不同规模数据中的适用性,可以适当松弛2.1 节中的终止条件。通过设置一个可调节的终止阶数K,把终止条件改写为:在k阶寻优后,如果k=K-1,则寻优终止;或者在k阶寻优后,在进行k+1 寻优时,如果不存在k+1 阶递增路径,则寻优终止。这一调整使得每一个包含的用户数量不超过K个。与原始终止条件相比,上述处理大幅提高了整体寻优效率。在4.2 节中,比较了LLC 方法(有和没有K)与其他算法在用时方面的性能。
第2 个问题是当待检用户中含有非固定比例的窃电用户时,LLC 方法可能失效。为此,需要在LLC 的计算流程中增加一道闭锁环节,以规避这一问题。需要说明的是,随着非固定比例窃电用户数量的增加,和ω*将不再满足式(11)所示的线性方程,LLC 搜寻得到的与ω*的线性相关性也越来越弱。附录A 表A2 中Fcov(ω*,)和Fp(ω*,)的变化也体现了这一结论,其中为最优解的表计 向 量。 因 此,可 以 利 用Fcov(ω*,) 和Fp(ω*,)来判别分析的场景是否为固定比例窃电场景。由于皮尔森相关性系数的取值范围固定在[-1,1]之间,Fp(ω*,)更适合作为LLC 目标场景的判断标准。设定阈值θ,当Fp(ω*,)>θ时,认为分析的场景以固定比例窃电为主,输出嫌疑用户集合Csus=Pmax;当Fp(ω*,)≤θ时,认为分析对象不是目标场景,为了避免算法失效,输出Csus=∅,闭锁LLC。为了在实际未知的情况下取得较好的检测效果,本文在经过大量的试验后建议θ取值范围为0.96~0.98。
2.3 检测框架
基于上述原理和求解过程,本文提出了LLC 在实际情景下的检测框架,由预处理环节、检测环节和判断环节组成,如附录A 图A3 所示。
假设某台区包含了用户M天的表计电量数据,对每一个用户i,预处理环节把第d天的表计电量向量化得到u~i,d。然后由式(4)计算台区的NTL 并向量化,得到每d天的NTL 向量ωd,并按式(8)对所有向量进行标准处理得到和。

最后按嫌疑度γi大小降序排列,得到待检用户的嫌疑度排名pi。最终选择排名最靠前的若干个用户进行现场稽查。
3 数据集及评价指标说明
3.1 数据集说明
1)正常数据集
采用中国某省电力公司提供的用电数据作为正常数据集来进行数值试验,该数据集的信息如附录A 表A3 所示。因该数据集所有用户均来自线损率低于3%的台区,可以认为均为正常用户。该数据集包含3 000 个单相用户和500 个三相用户285 d(2019 年4 月1 日—2019 年12 月31 日)的电压、电流、功率因数、用电量等用电数据,所有数据每15 min 记录一次。
2)窃电数据集
依托窃电仿真模拟实验平台(electricity theft emulator,ETE)对正常数据进行窃电改造,生成验证所需的窃电数据集。该平台结构如附录A 图A4所示,它主要由负载、负载控制区和电能表区3 个部分组成,是一个物理仿真实验平台。在生成窃电数据时,通过负载控制界面输入正常用户电压、电流和功率因数的时间序列,负载可以模拟该用户的真实用电过程。同时,负载的用电数据将被电能表记录并上传。如果电能表被篡改,如电流线圈欠流,该电能表所记录的数据就是该用户采用欠流法进行窃电的窃电数据。通过复现真实场景中存在的各种改表方式,该平台能够准确且灵活地模拟各种真实的物理窃电手法。由该平台生成的部分窃电样本如附录A 图A5 所 示。
本文主要采用欠压法、欠流法和部分移相法等固定比例的窃电手法来生成试验所需要的窃电数据,相关窃电手法的具体实现方式可参见文献[2]。
3.2 评价指标说明
采用广泛应用于机器学习领域分类评估的2 种指标对检测结果的准确度进行评价:曲线下方面积(aera under curve,AUC)和 平 均 查 准 度(mean average precision,MAP)。
AUC 指的是受试者工作特性(receiver operating characteristic,ROC)曲线下方的面积。ROC 曲线是查全率(true positive rate,TPR)和误报率(false positive rate,FPR)随模型阈值变化的轨迹。除了绘制ROC 曲线外,还可以直接计算AUC[21],表达式为:
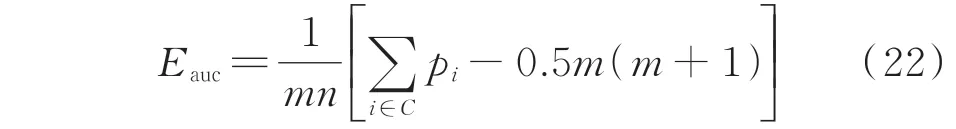
式 中:Eauc为AUC 的 数 值,且Eauc∈(0,1);m和n分别为窃电用户数量和正常用户数量。Eauc越接近1,检测效果越好。与FPR 和TPR 相比,AUC 能更加综合地表征模型的检测特性及检测准确度。
MAP 常应用于评价信息检索的准确度[22]。为了计算MAP,先定义查准率为:

式中:s为排名最靠前的若干用户中,最后一个用户的排名;y为排名最靠前的s个用户中窃电用户的数量;f(s)为查准率,代表排名最靠前的s个用户中窃电用户的占比。
然后,按照式(24)计算MAP 的值:
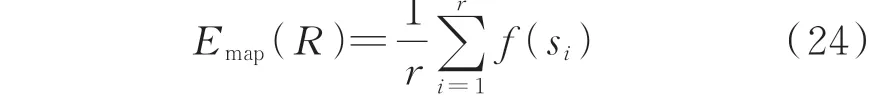
式中:Emap(R)为MAP 的值,且Emap∈[0,1];r为排名最靠前的R个用户中窃电用户的数量;si为排名最靠前的R个用户中第i个窃电用户的排名。
可以看出Emap(R)衡量的是窃电用户在输出的嫌疑名单中靠前的程度:窃电用户排名越靠前,Emap(R)的值就越接近1;反之,如果输出的前R个用户中没有窃电用户,则Emap(R) 为0。当然,Emap(R)的大小也与R的取值有关。本文取R为40来评价检测方法的准确率。需要说明的是,本文在计算Eauc和Emap(40)时所使用的排名均为2.3 节按嫌疑度γi降序排列得到的pi。
3.3 对比检测方法说明
为了分析LLC 方法的优势及不足,选择其他几种相关性分析方法和基于用电行为模式的检测方法进行对比:
1)PCC[23]:可以表征2 个变量的线性相关程度,PCC 越大,窃电嫌疑越高。
2)MIC[23]:可有效表征2 个变量非线性相关程度的量度,以MIC 作为窃电嫌疑度,MIC 越大,窃电嫌疑越高。
3)CFSFDP[24]:一种新型的基于密度和距离的聚类算法,文献[16]将这一算法改造成离群点检测算法用于窃电辨识。本文以文献[16]改造后的CFSFDP 作为对比方法。
4)局部离群因数(local outlier factor,LOF)[25]:经典的基于局部密度的离群点检测方法,LOF 值越大窃电嫌疑越高。
4 验证及评估
4.1 试验1
在第1 组试验中,首先选择61 d 的数据,将500 个三相用户均分成10 组,代表10 个供电台区。每个台区选择5 个用户进行窃电改造。改造的窃电手法从3.1 节的几种固定比例的窃电方式中随机选取。最终,每个台区窃电用户占比为10%。此外,为了说明NTL 和用户表计电量的随机分布特性,附录A 图A6 展示了其中一个台区5 个窃电用户表计电量和NTL 的平均频率分布直方图与核密度分布。
通过台区的随机构造和窃电用户的随机选取,进行了100 次重复试验。5 种方法在100 次试验中的最优得分如表1 所示。5 种方法在100 次试验中Eauc和Emap(40)的平均值如图1(a)所示。由表1 和图1(a)可以看出,基于用电行为模式方法最高的Emap(40) 仅为0.323,而相关性分析方法最低的Emap(40)高达0.737,同时,2 类方法Eauc的得分也相差悬殊。这说明后者在固定比例窃电检测中的优越性。进一步分析在3 种相关性分析方法中,LLC 的Eauc和Emap(40) 都在0.95 以上,其得分在PCC(0.787,0.758)和MIC(0.768,0.737)的基础上提升了约25%,表明LLC 提高了这一类方法对群体性固定比例窃电用户的检测能力。

表1 试验1 的5 种检测方法的最优结果Table 1 Optimal results of five detection methods for test 1
5 种方法在100 次试验中Eauc和Emap(40)的标准差如图1(b)所示。可以看出,虽然LLC 的标准差略高于CFSFDP 和LOF,但是相比另外2 种相关性分析方法,LLC 在固定比例窃电场景下的检测稳定性具有更佳的检测稳定性。

图1 试验1 评估结果Fig.1 Evaluation results of test 1
4.2 试验2
试验2 主要测试5 种方法在不同规模待检样本下的检测耗时。 选择3 种不同的数据规模:15 500 条、30 500 条 和76 500 条,分 别 对 应500 个 三相用户31 d、61 d 和153 d 的负荷数据。同时,为了评估终止阶数K对LLC 方法检测耗时和检测准确率的影响,设置了不同终止阶数(K=20、15、10、5、3)。其余设置依然效仿试验1。测试平台为一台CPU 型号为AMD Ryzen 95900(主频为4.7 GHz),内存容量为64 GB的台式机。5种方法都是基于Python 3.8,它们各自的检测用时及准确率指标如图2 所示。

图2 试验2 评估结果Fig.2 Evaluation results of test 2
可以看出,MIC 和PCC 在不同规模待检样本中的检测用时均低于25 s,是5 种方法中用时最少的。与之相对应,LLC 处理完76 500 条待检样本耗时为93.75 s,几乎是MIC 时长的5 倍。而随着数据规模的增加,LLC 的检测用时逐渐倍增。上述结果表明,在处理大规模的待检样本时,LLC 确实面临着严重的耗时问题。
为了解决LLC 的这一问题,设置了可供调节的终止阶数K。从图2 可知,随着阶数K从20 减少至3,LLC 的检测用时也逐渐降低。同时,LLC 的Emap(40)和Eauc在整个过程中并没有显著下降,甚至在K=3 时,LLC 的Emap(40)仍然保持在0.85 以上。这一结果表明,可以通过设置终止阶数把LLC 的检测用时控制在合理的水平而不会引起检测准确率的显著降低。
4.3 试验3
为了进一步探究固定比例窃电用户数量的变化对不同检测方法的影响,在保证每个台区用户总数不变的情况下,将窃电用户数量从2 增加到16(步长为2),这一过程中不同方法的检测结果如图3 所示。可以看出,当窃电用户数量较少时,3 种相关性分析方法都具有很高的检测准确度;随着窃电用户的增加,PCC 和MIC 的Eauc迅速下降,且与LLC 的得分逐渐拉开。整个过程中,PCC 和MIC 的Eauc降幅分别为0.231 和0.251,而LLC 的降幅只有0.111;三者的Emap(40)也具有类似的变化。这表明此类用户群体性窃电的确会给PCC 和MIC 的检测准确度带来负面影响,且随着窃电用户数量的增加,这种负面影响会进一步加剧。LLC 得分虽然也有所降低,但总体依然保持在很高的水平,表明LLC 在此场景下优越的检测能力。因此,基于用电行为模式方法的Eauc和Emap(40)对窃电用户数量的变化并不敏感。

图3 随固定比例窃电用户数量变化的评估结果Fig.3 Evaluation results of changes with number of fixedratio electricity-theft users
4.4 试验4
1.3 节的分析证明了在所有窃电用户电量曲线都正相关时,LLC 输出嫌疑用户集合Csus必定包含窃电用户集合CR。但仍需考虑当窃电用户不满足给定条件或满足程度不同时,LLC 是否还具备相应的能力。为此,本节以平均余弦相似度作为衡量窃电用户电量曲线相关性强弱的指标。平均余弦相似度是一群窃电用户电量两两余弦相似度的算术平均值。它的大小及正负可以表征群窃电用户是否满足式(15)及满足的程度。本节选取10 组具有不同平均余弦相似度的用户作为窃电用户,且这10 组用户的平均余弦相似度近似均匀地分布在-1 到1 之间。5 种检测方法在这一变化过程中对应的Eauc变化如图4 所示。
由图4 可以看出,基于用电行为模式方法的Eauc在这一过程中并没有明显的起伏,表明了此类方法对于窃电用户相关性强弱变化并不敏感。而与此相反,3 种线损相关性方法的曲线显示,随着余弦相似度减小,3 种方法的Eauc有着不同程度下降。其中,LLC 的曲线以0 为界,当余弦相似度为正时,LLC的Eauc降幅极小;当余弦相似度为负时,LLC 的Eauc降幅开始增大。这表明当窃电用户电量曲线负相关时,的确会影响LLC 检测固定比例窃电用户的能力。尽管如此,LLC 的曲线依然在此过程中表现出了最佳的抗干扰性,且其最低的Eauc也达到了0.784,这表明LLC 具有更优的推广能力。
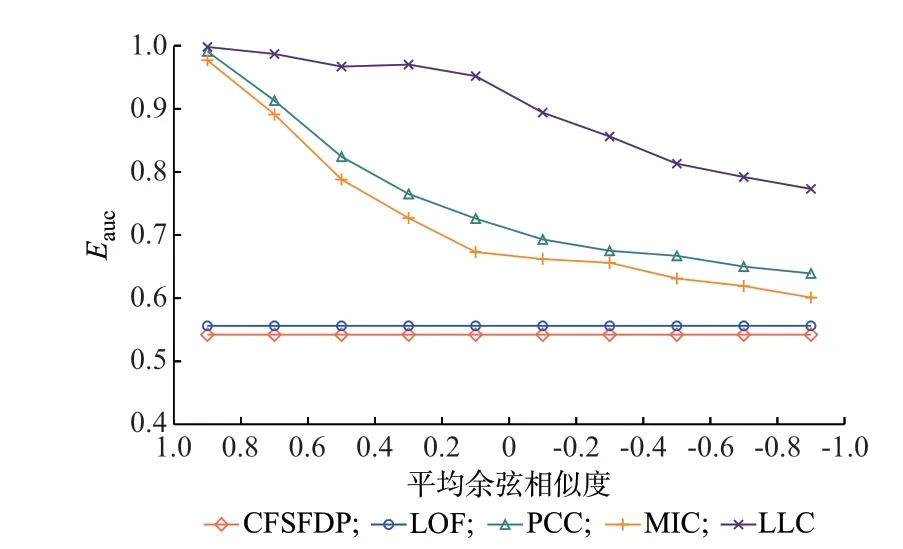
图4 不同平均余弦相似度的EaucFig.4 Eauc whith different average cosine similarities
5 结语
本文针对群体性固定比例窃电这一场景,提出了一种基于线损协方差分析的窃电辨识方法LLC,并通过中国某省电力公司的实测数据对LLC 方法的有效进行了验证。主要结论如下:
1)当任意两固定比例窃电用户电量曲线正相关时,窃电用户电量和NTL 之间的相关性存在着一种递增性质。
2)基于上述递增性质,通过搜寻线损协方差最大的用户组合,实现了对群体性固定比例窃电用户的检测。结果表明,LLC 的检测准确度在PCC 和MIC 的基础上提升了近25%。
当然,LLC 方法也存在一定的局限性。首先,该方法仅分析了用户电量数据和台区的NTL,利用的信息较为有限;其次,LLC 方法仅能检测线性攻击的固定比例窃电用户。因此,综合利用多源信息实现对非固定比例窃电用户的检测也是后续重点的研究方向之一。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
