基于广义变分原理的装配/残余效应下的结构力学特性分析

谭邹卿， 石晓灏， 蒋学东， 班书昊

(1.常州大学 机械与轨道交通学院， 江苏 常州 213164； 2.常州大学 生物医学工程与健康科学研究院， 江苏 常州 213164)

为了满足工程中各种功能的需求，需要设计各种各样的结构。例如，由于具有刚度高、结构轻、尺寸稳定性好等优点，桁架为工程中一种常用的结构[1-3]。另外，多层复合结构已广泛应用于机械、光学、电气和化学器件等领域[4-5]。然而，在实际工程中不可避免地会出现制造误差、安装误差、测量误差等因数，使得结构产生初始内力。初始内力的存在，必然会影响到结构的可靠性，甚至可能导致工程事故[6]。杆件长度的制造误差使得空间桁架产生一定的初始应力，这些未知的应力可能会引起局部杆件的过早屈曲，甚至造成整个桁架出现累积式坍塌[7]。对于多层复合结构，当制备和工作过程中存在表面应力、外延生长错配、温度变化、扩散应变等因数时[8-11]，由于涂层与基底存在失配应变，造成涂层-基底结构存在残余应力，进而引起多层复合结构的弯曲、剥离、脱层、屈曲以及断裂等行为[12-16]。因此，对装配/残余效应下结构力学特性的研究十分必要。

考虑装配/残余效应的结构是超静定的，其力学特性的研究是结构优化设计的一个关键问题。已有大量的方法研究装配/残余效应下结构力学特性，如连续介质理论[14,17-20]，Monte Carlo方法(MCM)[21-23]以及有限元法(FEM)[24]等。FURUYA[17]建立了一个解析模型，研究了杆件长度失配对空间结构灵敏度的影响。利用半解析方法，KARPOV等[18]研究了初始应力对规则晶格结构力学特性的影响。余俊等[6]阐述了考虑制造和安装误差对桁架结构各杆件的可靠性影响，并给出了修正的可靠性指标的计算方法。利用Monte Carlo方法，SHEIDAII等[23]研究了杆件长度随机分布对双层空间结构承载能力、坍塌以及可靠性的影响。SMITH等[24]利用有限元法求解了节点位置不确定条件下桁架结构的内力和位移。

此外，对层合结构残余效应的研究也广受关注。TIMOSHENKO[25]利用力和力矩平衡并结合变形协调条件，给出了热应力引起的双层梁弯曲的一般解。该方法被扩展到更为复杂的多层梁[26]。将总应变分解为均匀应变和弯曲应变，HSUEH等[14,16,27-28]利用三变量方法研究了多层系统的应力和变形。张能辉等[29-31]给出了更为简便的两变量方法。然而，上述方法适用于层合梁的残余效应研究，不便于分析桁架的装配效应。

尽管装配/残余效应的桁架和多层梁均属于超静定问题，但这些结构的一般解法尚未建立。目前，少量文献[32-33]基于广义变分原理研究了装配误差下桁架结构内力/应力问题，但不能直接求解其他复杂结构的装配/残余问题。本文利用拉格朗日乘数法建立了含装配/残余效应的新泛函，利用变分法得到结构支座反力或内力的矩阵形式的一般解，最后以空腹桁架、曲杆以及层合梁为例验证了该方法的正确性和通用性。

1 装配/残余效应下的广义变分原理

当系统达到平衡状态时，其余应变能函数将达到其最小值，属于极值问题。对有n个组件的线性超静定结构，采用拉格朗日乘数法得含装配/残余效应下的新泛函的一般形式为[20]

(1)

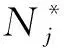
经过适当的简化或变换，式(1)可转为已有文献的理论。若不考虑装配/残余效应，式(1)可退化为经典的广义变分原理泛函[34-35]。若考虑超静定桁架，第j个组件的余应变能函数Vj仅是杆件轴力的函数，式(1)与文献[32-33]中的理论一致。

将支座反力或内力Nk及λi都当作独立的变分宗量，则新泛函L变分为

(2)

式中p为支座反力或内力的个数。

由于δNk及δλi都是独立的，则L的极值条件为：

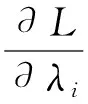
(3)

(4)

式(3)和式(4)分别表示静力学平衡方程和变形协调方程。由此可知，不同于传统的力法、位移法等，该能量法将求解超静定结构的支座反力或内力，转化为求系统相应的无条件广义变分原理的新泛函极值问题。

2 装配/残余效应下的矩阵解

考虑装配/残余效应下线性超静定结构，其m个独立平衡方程的一般形式为

(5)

式中aij为支座反力或内力的系数。

第j个构件的余应变能函数为

(6)

将式(5)和式(6)代入式(4)得

(7)

将式(5)和式(7)改写成矩阵形式为

(8)

式中：A和B分别为式(5)和式(7)的系数矩阵；AT为A的转置矩阵；N为支座反力或内力的向量；Λ为拉格朗日乘子的向量；Ne为装配/残余效应的向量。

求解式(8)得[20,36]

(9)

式中:C11=B-1-B-1AT(AB-1AT)-1AB-1;C12=B-1AT(AB-1AT)-1;C21=(AB-1AT)-1AB-1;C22=-(AB-1AT)-1。

利用式(9)得广义力(支座反力或内力)为

N=C11Ne

(10)

3 结果与讨论

为了验证装配/残余效应下能量模型的正确性，下面将讨论空腹桁架、曲杆以及层合梁3种实例，并将计算结果与现有结果进行对比。

3.1 算例1:装配效应下的空腹桁架

如图1(a)所示空腹桁架结构，悬臂梁AB和CD长度均为l，抗弯刚度均为E1I1。杆BD略长于名义长度l/2，其制造误差为Δ，抗拉压刚度为E2A2。试求杆BD的装配内力。

对梁AB进行受力分析，如图1(b)所示。由静力平衡条件可知:

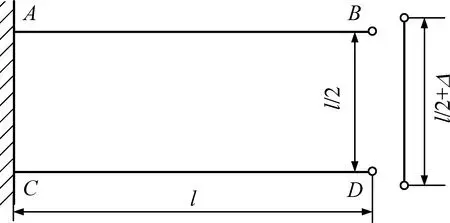
(a) 空腹桁架示意图

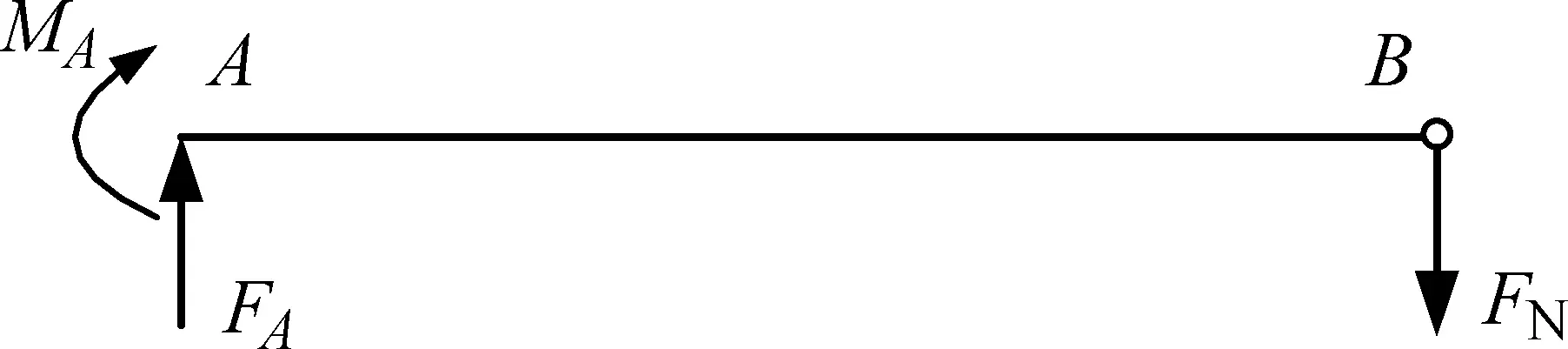
(b) AB的受力图图1 装配效应下的空腹桁架 Fig.1 Assembly effect on a vierendeel truss

FA-FN=0

(11)

MA+lFN=0

(12)

式中:FN为杆BD的轴力;FA和MA分别为固定端A处的约束力和约束力偶。

对细长梁，剪切变形能影响较小，因此忽略剪切应变对梁应变能的影响。考虑到载荷和结构的对称性，根据式(1)得新泛函为

(13)

式中λi(i=1，2)为拉格朗日乘子。

将FN，FA和MA都当作独立变量，由式(13)得：

(14)

(15)

(16)

将式(11)、式(12)和式(14)至式(16)写成矩阵形式

(17)

求解式(17)得杆BD的装配内力为

(18)

式中负号表明杆BD受压力。上式与文献[37]中的计算结果完全一致，说明了该能量法的正确性。

3.2 算例2:装配效应下的曲杆

如图2(a)所示的曲杆结构，由弹性圆杆AB和刚杆BC组成，在C端上方有一垂直的直杆。已知杆AB的长度为l，材料的抗弯刚度和抗扭刚度分别为EI和GIp。杆BC的长度为a。杆CD的加工长度比名义长度h略短，加工误差为Δ，材料的抗拉压刚度为EA。试求杆CD的装配内力。

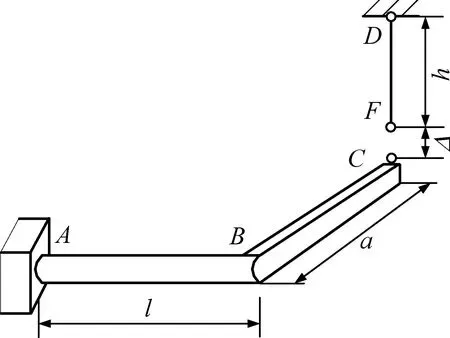
(a) 曲杆示意图

(b) 曲杆AC的受力图图2 装配效应下的曲杆 Fig.2 Assembly effect on a curved bar

对曲杆AC进行受力分析，如图2(b)所示。由静力平衡条件可知:

FA-FN=0

(19)

TA-aFN=0

(20)

MA-lFN=0

(21)

式中:FN为杆CD的装配轴力;FA，TA和MA为固定端A处的约束反力。

考虑杆件的拉压应变能、扭转应变能以及弯曲应变能，根据式(1)得新泛函为

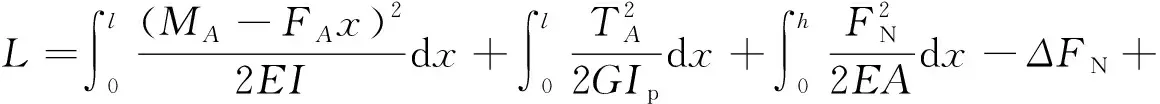
(22)

式中λi(i=1，2，3)为拉格朗日乘子。

将FN，FA，TA和MA都当作独立变量，由式(22)得:

(23)

(24)

(25)

(26)

将式(19)至式(21)、式(23)至式(26)写成矩阵形式为

(27)

求解式(27)得杆CD轴力为

(28)

上式与文献[37]中的计算结果完全一致，说明了该方法能够求解装配效应下的曲杆内力问题。

3.3 算例3:残余应变效应下的双层悬臂梁

最后考虑残余应变效应下的双层悬臂梁，其结构图以及初始残余应变分布如图3(a)所示。双层悬臂梁的长度和宽度分别为l和b。各层的厚度、横截面面积、惯性矩、弹性模量、残余应变分别为hi，Ai，Ii，Ei，εri(i=1，2)。试求残余应变效应下的双层悬臂梁的内力以及曲率半径。

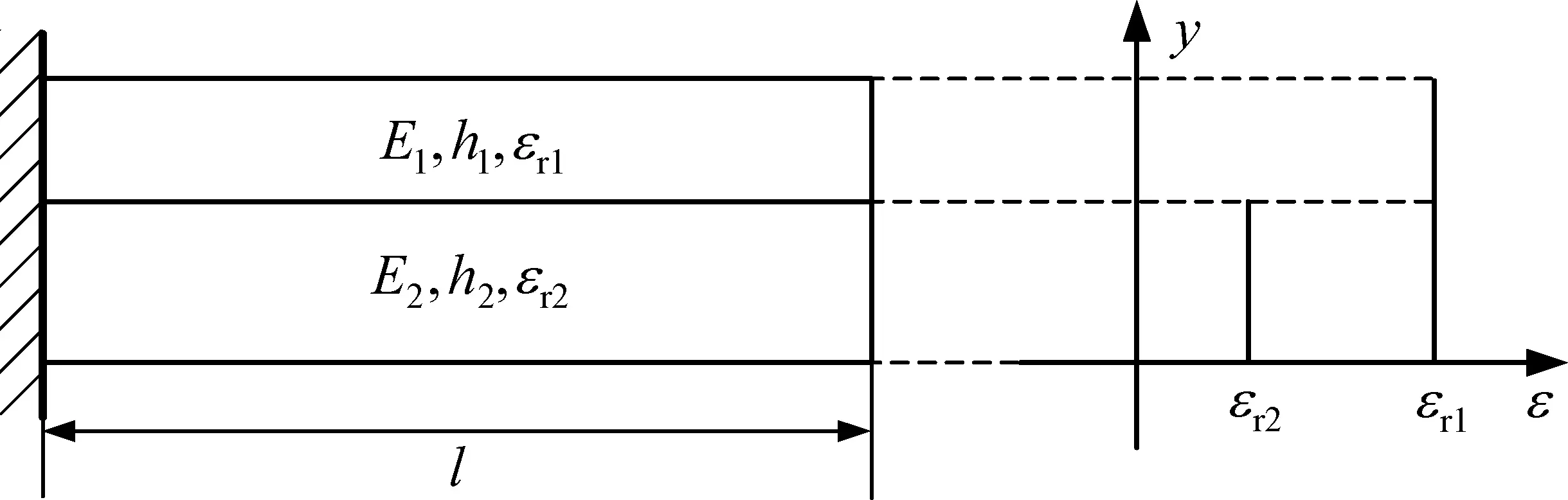
(a) 双层悬臂梁和初始残余应变分布示意图

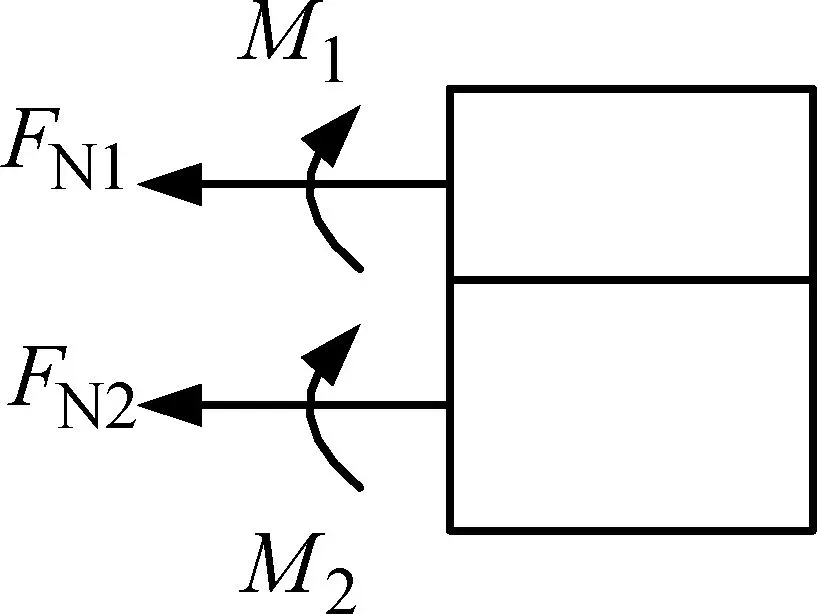
(b) 双层悬臂梁右截面的受力图>图3 残余应变效应下的双层悬臂梁 Fig.3 Residual strain effect on a bilayer cantilever beam

对双层悬臂梁进行受力分析，如图3(b)所示。由静力平衡条件可知:

FN1+FN2=0

(29)

(30)

式中FNi和Mi(i=1，2)为各层的轴力和弯矩。

忽略剪切应变对梁应变能的影响，根据式(1)得新泛函为

(31)

式中λi(i=1，2)为拉格朗日乘子。

将FN1，FN2，M1和M2都当作独立变量，由式(31)得：

(32)

(33)

(34)

(35)

将式(29)、式(30)和式(32)至式(35)写成如下矩阵形式

(36)

求解式(36)得双层悬臂梁的内力为:

(37)

(38)

(39)

式中K=4(E1A1+E2A2)(E1I1+E2I2)+E1A1E2A2(h1+h2)2。

根据欧拉-伯努利梁理论，悬臂梁各层受到的弯矩为

(40)

式中ρi(i=1，2)为各层的曲率半径。

考虑到梁的变形很小，曲率半径远大于梁的厚度，则各层具有相同的曲率半径，即ρ1=ρ2=ρ。因此，式(40)可简化为

(41)

由式(38)和式(41)可得双层悬臂梁的曲率半径为

(42)

上式与文献[38]中的计算结果完全一致，表明了该变分法能够求解残余应变效应下的双层悬臂梁的内力以及变形问题，进一步说明了该方法的通用性。

4 结 论

利用广义变分原理研究了装配/残余效应下超静定结构的力学特性。引入拉格朗日乘数并结合静力平衡条件，构造了考虑装配/残余效应的拉格朗日函数，求解其极值问题，给出了支座反力或内力矩阵形式的通解。为了验证该能量法的有效性，对比了空腹桁架、曲杆以及层合梁3种算例，结果表明了该方法在求解装配/残余效应下各种超静定结构力学特性具有良好的通用性。