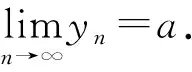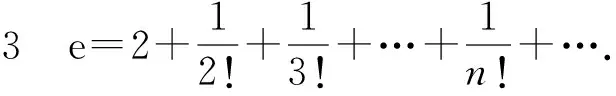极限的应用
2022-07-12山西省工业管理学校山西太原030012
◎杜 娟(山西省工业管理学校,山西 太原 030012)
1 引 言
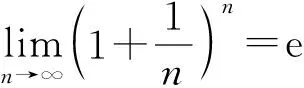
1.1 e在某些方面的应用

2 e的近似计算及应用
2.1 数e是无理数的几种证明方法
定理1 常数e是一个无理数.
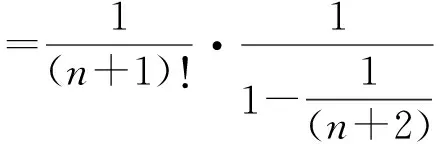
所以,
那么有
于是,

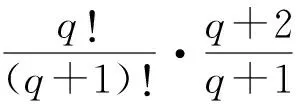
因此,e只能是一个无理数.
如果利用ex的泰勒展开式,我们还可以有另一种证法:考虑如果e是有理数的话,那么e-1也是一个有理数.
证法2 由ex的泰勒公式得
于是,



从而e-1只能是一个无理数,所以e也只能是一个无理数.
2.2 与e有关的不等式
2.2.1 与e有关的数列不等式:
问题:求出使得下列不等式成立的最大值α和最小值β:
解:对于上面的不等式,两边取以e为底的对数得
(1)

(2)
下面我们来证明f(x)是一个严格的单调减函数.对f(x)求导得
(3)
我们来证明:
(1+x)ln2(1+x) (4) 即要证: (5) 又g(0)=0,因此g(x)>0,x∈(0,1]. 从而,(5)式成立. 将(5)式的结果代入(3)式得f′(x)<0,x∈(0,1]. 因此,f(x)在(0,1]上是一个严格的单调减函数. 于是, (6) (7) 求解完毕. 2.2.2 证明对于所有的n>1,有如下的不等式成立: (1) 证明:下面的式子是等价的: (2) (3) (4) (5) 这样,我们在不等式(5)两边同时乘-1,得到等价式子: (6) 注意到 将上式代入不等式(6)中,得到 注意到k>1时,k 证明完毕. 2.3.1 在极限中的应用 当n≥2时, 证明:由2.1中的证法1, 于是, =ln(n+1)-lnn>0. 这说明数列{bn}单调减少有下界,从而收敛. 注:{bn}的极限γ=0.57721566490…称为Euler常数. 2.3.2 在级数中的应用 证明:最简单的是用数学归纳法. 当k=1时, 命题成立. 那么,当k+1时,有 则Fk+1也是e的整数倍. 于是,我们就有 定理1(夹逼准则) 如果数列{xn},{yn},{zn}满足下列条件: (ⅰ)xn≤yn≤zn(n=1,2,3……), 定理2(单调有界准则) 单调有界数列必有极限. 进一步,由 得到 由k的任意性,得到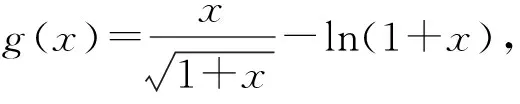
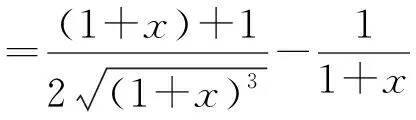
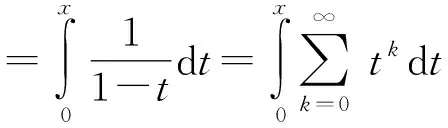
2.3 数e的广泛应用
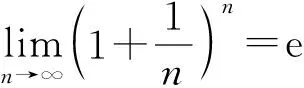
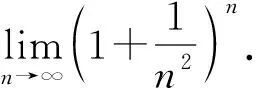
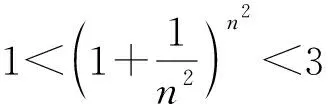
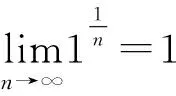
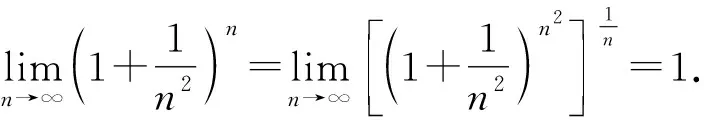
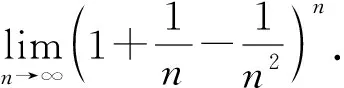
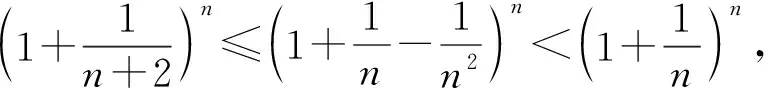
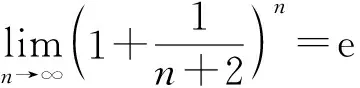
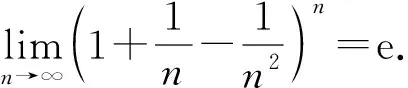
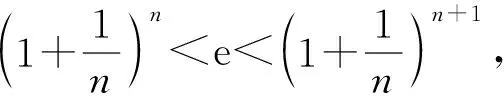
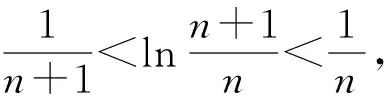
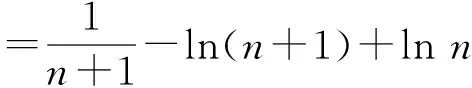
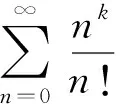



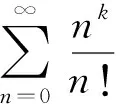


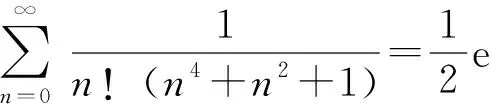
3 参考公式