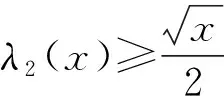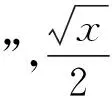揭示素数分布规律的阶准素数模型简介
2022-07-12冯军刚朱彦通西安石油大学机械学院陕西西安70065卡内基梅隆大学宾夕法尼亚州匹兹堡
◎冯军刚 朱彦通(西安石油大学机械学院,陕西 西安 70065;卡内基梅隆大学,宾夕法尼亚州 匹兹堡 5)
1 引 言
在后文参考文献[1]中,已经出现了“pn阶准素数模型”的雏形,只是没有系统地建立过该模型,且因其中的误差项,对误差界值论证过粗、估计过大、严重失真,致使该式失去了定量计算的意义,从而使该式一直被束之高阁.该式实际上就是计算不大于x的pn阶准素数数目πn(x)的上、下限的.其原型是:
(1)
在该式中:π(y)表示不大于y的素数的个数,本文设其为n,并将第n个素数记为pn,那么,π(y)便可用n取代;1+Φ(x;y)表示的是[0,x]上,筛去含有不大于y的素数因子的合数,所存留下来的正整数(本文称之为 “pn阶准素数”)的个数.于是,式(1)便被表示为:
(2)
2 pn阶准素数模型的特性简述

图1 [0,30]上的素数筛网示意图和素数元素分布图

图2 p3阶准素数第一个周期上的三层筛网示意图和准素数的分布图

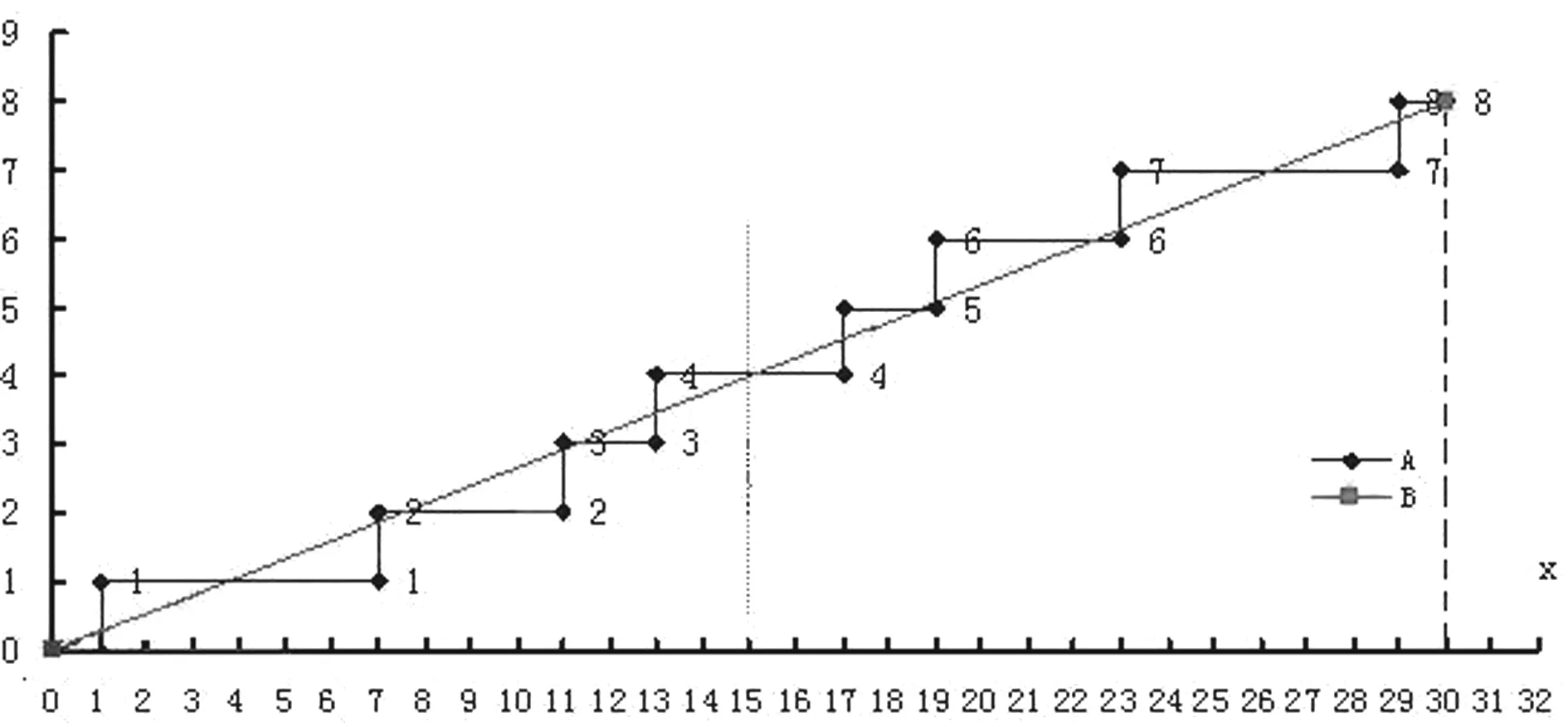
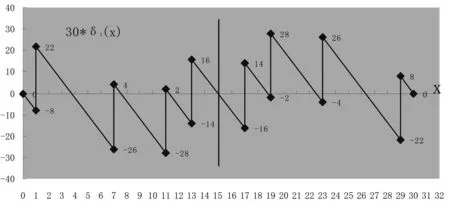
图3 (1)阶梯线π3(x)—A ;(2)直线(3)折线
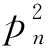
π(x)=πn(x)+(n-1);
(3)
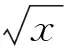
3 以素数“前密后疏”为镜鉴,证明误差δn(x)不大于n
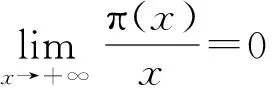
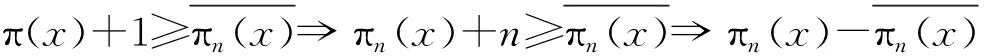
(4)
4 pn阶准素数模型的应用举例
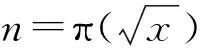
4.1 定量计算素数数目π(x)的上、下限及其底线,证明素数数目的无穷性
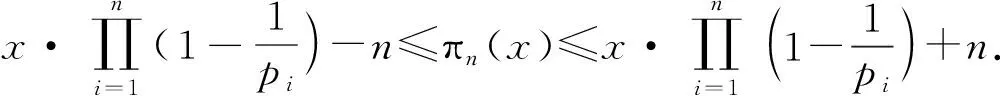
(5)
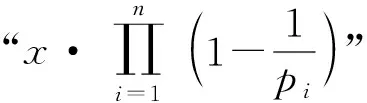
(6)
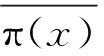
(7)
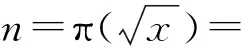
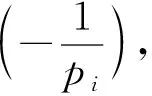
(8)
4.2 双筛计算“特定素数对”数目λ(x)及其底线,具结相关课题之证明
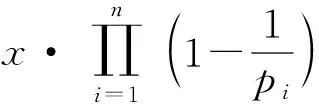
对于“单合数对”而言,这恰好将其减去了1次.但对于“双合数对”而言,它却被减去了2次,多减了1次.双筛计算的结果,一般只能是“双素数对”数目的不足近似值,只有x较小、“特定准素数对”中不存在“双合数对”时,才能更贴近真值.
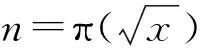
(9)
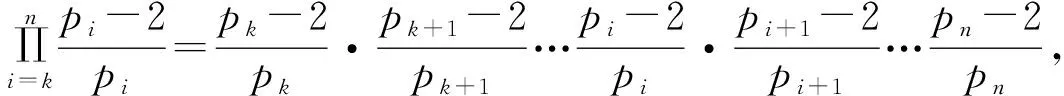
(10)
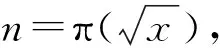
(11)
4.2.1 计算“和等于偶数x的特定素数对”:“1+1”的数目λ1(x)的底线,证明任意偶数一定存在“素分割对”

(12)
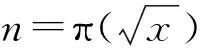
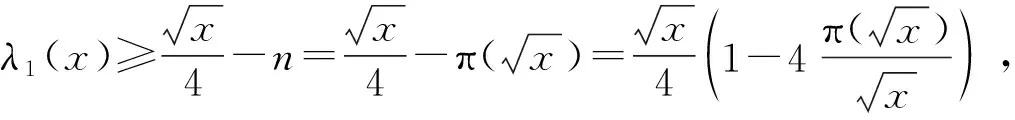
(13)
根据文献[1]第379页定理5的结论,当x→∞时,则有:
(14)
(15)
式(12)(15)证明:对于任意偶数x,其素分割对“1+1”的数目的底线是x的递增函数;x足够大以后的任意偶数,都一定有素分割对“1+1”存在.
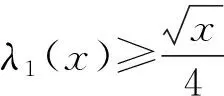
4.2.2计算差等于2的特定素数对——孪生素数在[0,x]上的数目λ2(x)的底线,证明孪生素数的无穷性
奇数序列虽是筛选“1+1”的“双筛始序列”,但并非筛选“孪生素数对”的“双筛始序列”.因为每个奇数与其前后紧邻的两个奇数,都构成了“孪生奇数对”,它们显然不是相互独立的,筛掉中间这个奇数,就筛掉了两对“孪生奇数对”,而“双筛计算”却只减掉了一对.用p2阶筛网继续单筛奇数序列,所得的p2阶准素数序列,才是筛选“孪生素数对”恰当的“双筛始序列”.因为p2阶准素数周期为6,每个周期内只有两个准素数元素,分别紧挨着前后端点.如此每个p2阶周期端点两侧的两个准素数(如5和7),皆构成了一对独立的、差为2的“孪生准素数对”.所以,用λ2(x)表示差为2的“孪生素数对”的数目,在式(11)中,代入双筛起始序号k=3,得:
(16)
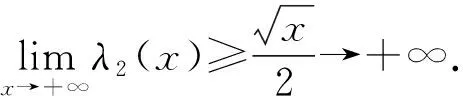
(17)