Life-cycle failure probability analysis of deteriorated RC bridges under multiple hazards of earthquakes and strong winds

Zheng Xiaowei and Li Hongnan

1.Jiangsu Key Laboratory of Environmental Impact and Structural Safety in Engineering, School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, China

2.State Lab.of Coastal and Offshore Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology,Dalian 116024, China

Abstract: Engineering structures may be exposed to one or more extreme hazards during their life-cycles.Current structural design specifications usually treat multiple hazards separately in designing structures and there is a limited probabilistic basis on extreme load combinations.Additionally, the performance of engineering structures will be deteriorated by the aggressive environments during their service periods, such as chloride attack, concrete carbonation, and wind-induced fatigue.This study presents a probabilistic methodology to assess the time-dependent failure probability of RC bridges with chloride-induced corrosion under the multiple hazards of earthquakes and strong winds.The loss of cross-section area of reinforcements and the reduction in strength of reinforcing steel and concrete cover induced by the chloride attack are considered.Moreover,the Poisson model is employed to obtain the occurrence probabilities of the individual and concurrent earthquake and strong wind events.The convolution integral is used to determine the joint probability distribution of combined load effects under simultaneous earthquakes and strong winds.Numerical results indicate that the structural failure probability under multiple hazards increases significantly during the bridge′s life-cycle due to the chloride corrosion effect.The contribution of each hazard event on the total structural failure probability varies with time.Thus, neglecting the combined influences of multiple hazards and chloride-induced corrosion may bring erroneous predictions in failure probability estimates of RC bridges.

Keywords: life-cycle; multihazard; chloride; occurrence model; failure probability

1 Introduction

Reinforced concrete (RC) bridges are inevitably exposed to multiple hazards (also referred to as multihazard or MH loads) during their service life, e.g.,earthquakes, strong winds and blasts.In multihazardprone areas, the disaster-resistant designs of RC bridges are commonly carried out based on the worst load effects associated with the individual hazard (Grünthalet al.,2006).As specified in ASCE 7-05 (ASCE, 2005), the structural safety under earthquakes and strong winds are ensured by the envelope of individual hazard demands.The capacity of these bridges may not be sufficient to deal with multihazard effects.Furthermore, RC bridges will deteriorate as the service lifetime due to the aggressive environments, e.g., chloride-induced corrosion.As a result, the capability of RC bridges to resist different hazards will decrease as the service period increases.Therefore, it is necessary to investigate the performance of RC bridges considering the combined effects of chloride corrosion and multihazard-induced load effects.

In dealing with the combination of MH extreme loads, the load factors representing the occurrence probability of loads are commonly employed in current codes.The probabilistic methods commonly used for MH load combinations include (1) Turkstra′s rule (Turkstra and Madsen, 1980); (2) Ferry-Borges model (ACI, 1971); and (3) Wen′s load coincidence method (Wen, 1977).Some researchers systemically investigated the performance of structures subjected to MH loads.Wenet al.(1994) developed a comprehensive reliability-based design procedure for buildings under combined time-varying loads based on the load coincidence method.Asproneet al.(2010) proposed a probabilistic model for the multihazard risk assessment of RC structures subjected to earthquake and blast loads.Liang and Lee (2012a; 2012b; 2013a; 2013b; 2013c)proposed an analytical framework for the structural failure probability analyses of bridges under seismic and live loads.However, the total failure probability of theexample bridge was not provided in their study and the results were semi-quantitative.

The severe structural damage and large economic loss suffered from past earthquakes and strong winds have highlighted the necessity of comprehensively considering these hazards in the design of engineering structures.Wen and Kang (2001a; 2001b) proposed the minimum life-cycle cost design criteria for buildings subjected to earthquakes and strong winds, but the simultaneous occurrence of these two hazards was ignored in their study.Duthinh and Simiu (2009)revealed that current specifications may fail to leave enough margin for structures located at regions prone to earthquake and strong wind events.Moreover, other efforts were devoted to structural risk assessment under the multiple hazards of strong winds/hurricanes and earthquakes, such as Li and Ellingwood (2009) and Kameshwar and Padgett (2014).Note that concurrent earthquakes and winds are not considered in previous studies.This is most likely because of the traditional opinion that assumes the simultaneous occurrence probability of earthquakes and strong winds can be ignored.However, Liet al.(2019; 2020) did much work on the statistic and analysis of recoded and historical earthquake and strong wind data.They found that the joint occurrence probability of extreme events like simultaneously having earthquakes and strong winds cannot be neglected, especially an earthquake with weak and a wind event with moderate intensities.In addition, when super typhoon Jebi struck the west coast of Hokkaido, Japan on 2018/9/5, on the same day a ML4.4 earthquake occurred at Peninsula, Hokkaido(Zhenget al., 2019b).Coincidentally, an earthquake with a magnitude of 5.7 and the super typhoon Hagibis simultaneously occurred in the Kanto region of Japan on Oct.12, 2019.Some researchers indicated that the local atmospheric pressure will vastly change when an earthquake occurs (Jinet al., 2011; Kozaket al., 2004;Singhet al., 2010; Watadaet al., 2006), which might be the reason why earthquake occurrences were always accompanied with strong winds (Gao and Yang, 1981;Xuet al., 1993; Yinet al., 1999).In this context, Zhenget al.(2019b) assessed the risk of a high-rise building under seismic and wind loads, and indicated that the risk estimates are mainly dominated by the event of simultaneous earthquakes and strong winds.Therefore,it is necessary to understand the structural behavior against multiple hazards, such as earthquakes and strong winds.

During the service lifetime of engineering structures,the structural capacities resisting extreme natural hazards may be inevitably deteriorated due to corrosion effects in a harsh environment.Chloride-induced corrosion is the main source that leads to structural performance degradation of RC bridges, especially for those exposed to marine environments or deicing salts (Enright and Frangopol, 1998; Stewart and Rosowsky, 1998b).There has been significant research on assessing the impacts of chloride-induced corrosion on structural performance,e.g., Stewart and Rosowsky (1998a), Valet al.(1998),Ghosh and Padgett (2010) and Biondiniet al.(2014).However, these previous studies are mainly focused on the life-cycle performance of RC bridges with chlorideinduced corrosion under an individual hazard.Studies on the life-cycle performance assessment of deteriorated RC structures under multiple hazards are very rare.Mori and Ellingwood (1993) presented a probabilistic framework to estimate the time-dependent reliabilities of deteriorated RC structures under MH loads.However,the concurrent hazard effects were not considered in calculating the structural failure probability.

This study proposes a life-cycle failure probability analysis methodology for RC bridge structures under multiple hazards of earthquakes and strong winds.In the next section, the basic procedure for a time-dependent failure probability analysis of RC structures under multiple hazards is presented by considering the effects of chloride corrosion.In Section 3, the proposed approach is illustrated in an RC bridge, which is simplified to an equivalent single-degree-of-freedom (SDOF) model.The probability density functions of structural deformations under the individual hazard and concurrent multiple hazards are calculated in Section 4.In Section 5, the numerical simulation results are presented and discussed in detail.Finally, Section 6 provides a summary of this research with some concluding remarks.

2 Time-dependent failure probability under multiple hazards

The life-cycle failure probability analysis of infrastructure subjected to multiple hazards includes the occurrence probability estimation of individual and concurrent hazards, the time-dependent model of chloride corrosion, and the probabilistic response analysis of structures under MH loads.

2.1 Time-dependent partial and total failure probabilities

Due to the effects of aggressive environments, the performance of engineering structures will deteriorate during their service life.Thus, the failure probabilities will increase with time; the time-dependent structural failure probability, denoted bypf(t), is written by,

wheretrepresents the service period;R(t) andL(t) are the time-dependent structural resistance capacity and load effect, respectively.

In load combination methods (Ghosnet al., 2003),the dead load, commonly assumed to be time-invariant,can be directly added to time-varying loads.Therefore,only the effects induced by time-varying loads during thestructure′s lifetime are taken into consideration in this study.Two different kinds of time-varying loads, denoted byL1andL2, are considered in the load combination.Thus, Eq.(1) can be rewritten by,

The structural failure under MH loads can be disintegrated into three cases (Liang and Lee, 2012a;Wenet al., 1994) (1) the individual load effectL1(t)is greater than or equal toR(t); (2) the combined load effect is greater than or equalR(t), but no individual load effect is; and (3) the individual load effectL2(t) is greater than or equal toR(t).The probability of each case is referred to as the partial structural failure probability.Based on the concept of conditional probability, each partial structural failure probability can be expressed as the product of the conditional failure probability and the occurrence probability of each hazard event.The total structural failure probability can be obtained by adding up all the partial failure probabilities (Wen, 1977).Then,the combined factor involved in the load combination function can be obtained based on the ratio between the partial failure probability under each hazard and the total probability due to all hazards.Moreover, it is assumed that a load must exist (i.e., without the case of no load)in calculating the occurrence probability of each hazard event.Thus, Eq.(2) can be further rewritten by (Liang and Lee, 2012a; Wenet al., 1994; Wen, 1977),

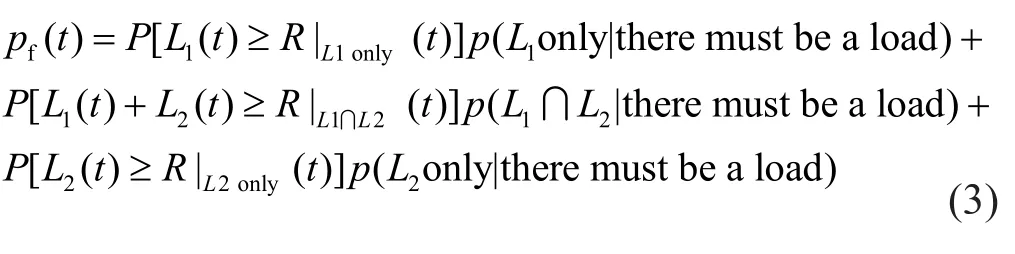
whereP(·|·) denotes the conditional failure probability;p(·|·) denotes the occurrence probability of hazard event (·); and the symbol “∩” represents simultaneous occurrence.

To simplify the format of Eq.(3), the conditional failure probability under the individual load effectL1can be expressed by,

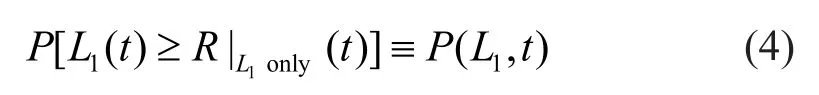
It should be emphasized that the occurrence probability of a hazard event is under the condition of“there must be a load” in Eq.(3).In other words, the probability for the individual occurrence ofL1(withoutL2) is a conditional probability, which can be written as,

in which the overhead bar stands for “no load occurrence”,pΣdenotes the occurrence probability of “there must be a load”, which can be divided into three conditions: (1)the occurrence probability of loadL1only (without loadL2), denoted by; (2) the simultaneous occurrence probability of loadsL1andL2, denoted by; and (3)the occurrence probability of loadL2only (without loadL1), denoted by.Thus,pΣcan be written as,

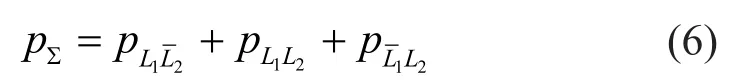
According to Eqs.(4) and (5), the partial structural failure probability induced by individual loadL1(withoutL2) at timet, namely(t), can be expressed by,

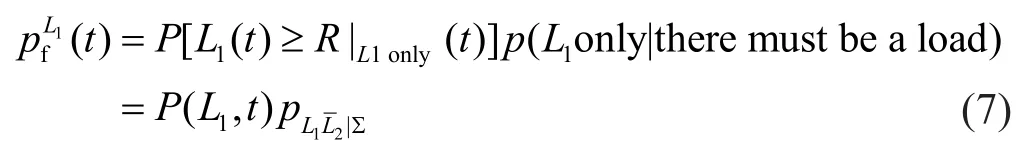
Analogously, the time-dependent partial failure probabilities attributed to the concurrent loadsL1andL2as well as the individual loadL2(withoutL1) can be written in the same format of Eq.(7), respectively.The total failure probability of a structure at any time spot in its service life can be obtained by rewriting Eq.(3) as,

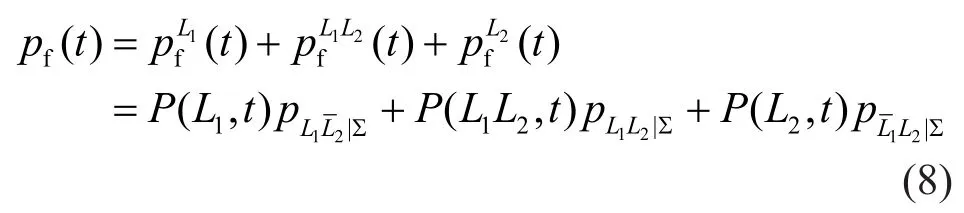
In the following discussion, the loadsL1andL2are,respectively, replaced byEandWto represent seismic and wind loads.The lifecycle total failure probability of a structure under earthquakes and strong winds can be expressed by,

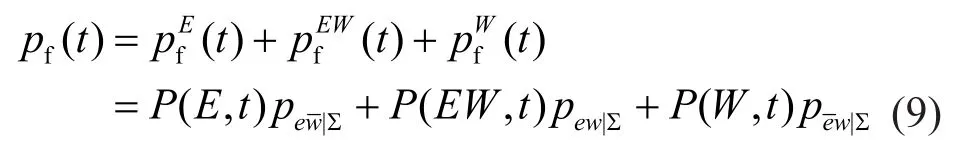
The schematic diagram of structural failure probability at timetis shown in Fig.1.Note that when the effect induced by an individual time-varying load reaches the maximum valuex, there is no chance for other load effects (combined load effects is regarded as a special kind of individual load effect) to reach this specific levelx.In other words, when an individualload effect reaches a certain maximum levelx, the structural responses caused by individual strong winds and simultaneous earthquakes and strong winds should be less than the threshold of the structure′s capacityx.The time-dependent failure probability can be expressed as the integral form if the probability density functions(PDFs) of seismic and wind load effects are known.At any spot of a structure′s lifetime, the failure probability attributed to individual seismic load can be expressed as,

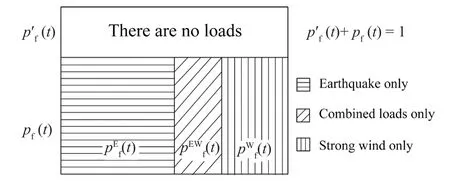
Fig.1 Total structural failure probability under multiple hazards

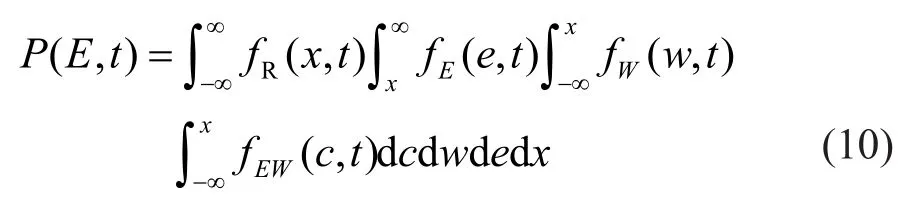
wherefE(e,t),fEW(c,t) andfW(w,t) denote the timedependent PDFs of the single seismic load effect, the combined load effects induced by the simultaneous earthquakes and strong winds and the single load effect of strong winds, respectively.

Analogously, the time-dependent conditional failure probabilityP(EW,t) andP(W,t) are, respectively,obtained by,

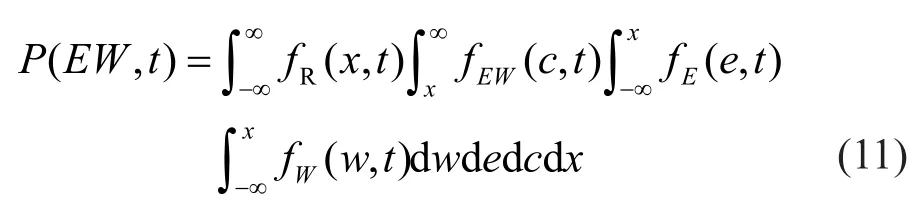
and

In this study, the earthquakes and strong winds are assumed to be statistically independent.The joint probability density of the combined earthquake and strong wind load effects can be obtained by using the convolution integral (Mori and Ellingwood, 1993), as shown in Eq.(13).

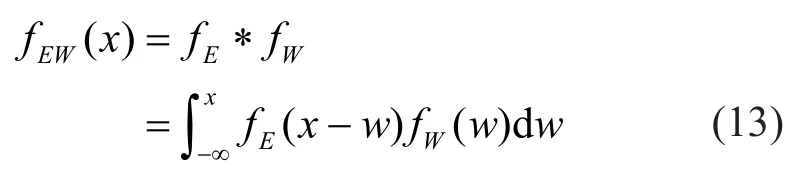
where the symbol “*” represents convolution.Note that the convolution integral method is only suitable for a linear system.Thus, the nonlinear responses of the bridge are not considered in this study.

2.2 Occurrence probability of each event

To calculate the occurrence probability of each event, some assumptions are made: (1) the occurrence frequencies of the earthquakes and strong winds within the time intervaltfollow the Poisson distribution(Kafali, 2008); (2) the occurrences of earthquakes and strong winds are mutual independent in non-overlapping intervals; and (3) the probability of two earthquakes occurring in a small interval (regardless of the main aftershocks) is zero.

2.2.1 Occurrence probability of individual hazard

Based on the Poisson model assumption, the occurrence probabilities of earthquakes and strong winds in structures′ lifetime (TH) can be, respectively,expressed as,

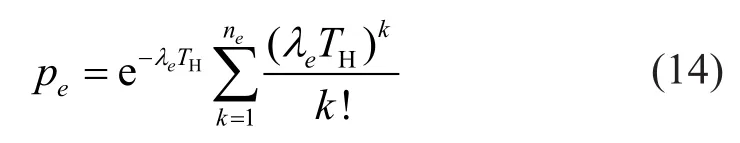
and

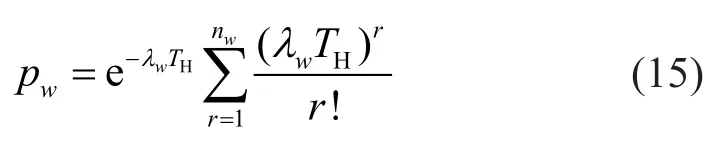
in whichλeandλware the occurrence rates of earthquakes and strong winds, respectively; andneandnware the occurrence times of earthquakes and strong winds duringTH, respectively.The occurrence probability of an earthquake inTHis the summation of the individual occurrence probability of an earthquake () and concurrent occurrence probability of these two hazards(pew).Thus,can be calculated by,

Similarly, the probability of only having strong winds can be written in the same format as that of Eq.(16).As mentioned above, the conditional occurrence probabilities of only having earthquakes() and only having strong winds () can be,respectively, written as,

and

2.2.2 Simultaneous occurrence probability of multiple hazards

Based on the third assumption mentioned above,there is only one earthquake in the duration of strong wind (tw).For simplicity, the durations of strong wind events in the structure′s life-cycle are assumed to be the same in this study.Letrdenote the occurrence number of strong winds, the occurrence probability ofrearthquakes in the total duration of strong winds (rtw)can be calculated by,

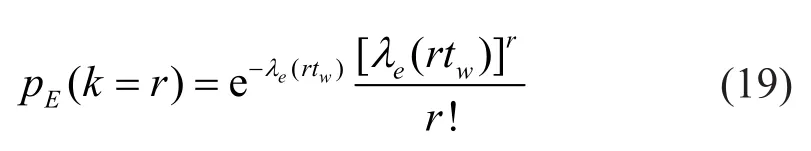
where the occurrence rate of an earthquake (λe) can be calculated by the reciprocal of earthquake return period;the duration of each strong wind event (tw) is assumed to be 10 minutes (GB50009-2012, 2012).

Note that in other published research (Liet al.,2019; Zhenget al., 2019b), 445 earthquake data withMs≥4 from 1971 to 2017 from the China Strong Motion Network Centre and 2944 strong wind data withv≥10 m/s from 1971 to 2017 from the China Meteorological Administration were collected by the authors.After obtaining the earthquake and strong wind data, the number of pairs with simultaneous earthquakes and strong winds is 76.In other words, the extreme event of simultaneous earthquakes and strong winds should be carefully investigated rather than neglected groundless.Thus, the simultaneous occurrence probability of earthquakes and strong winds in the structure′s service life (pew) can be obtained by,

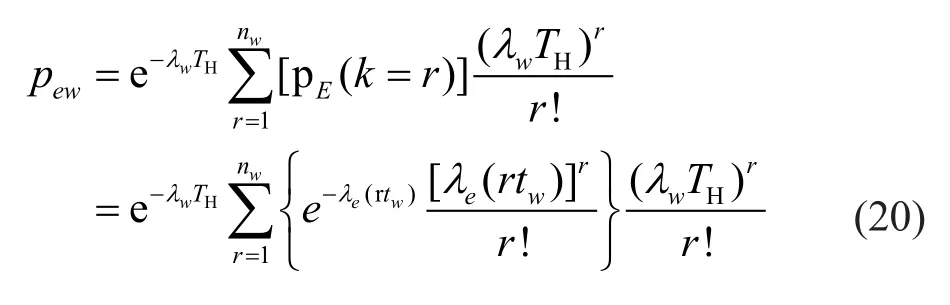
The conditional probability for the simultaneous occurrence of an earthquake and strong wind (pew|Σ) can be expressed as,

2.3 Time-dependent chloride-induced corrosion model

The diffusion process of chloride ions in the concrete cover of structural members can be represented by Fick′s second law (Valet al., 1998).The reinforcing steels start to corrode when the concentration of chloride ions at the surface of reinforcements reaches a threshold.The corrosion initiation time of reinforcing steels can be calculated by (Stewart and Rosowsky, 1998a),

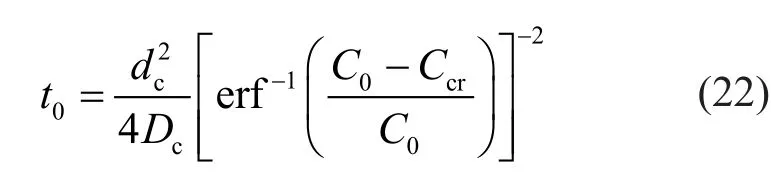
wheret0denotes the corrosion initiation time;dcis the thickness of the cover concrete;Dcis the coefficient of diffusion;C0is the chloride concentration on the concrete surface, andCcris the critical chloride concentration corresponding to corrosion initiation.

Based on the experimental data reported by Liu and Weyers (1998), Vu and Stewart (2000) developed an empirical equation to calculate the time-varying chloride corrosion current density,

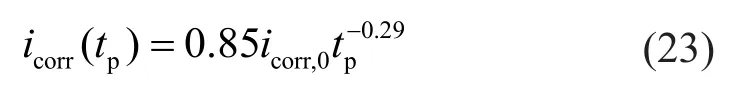
and

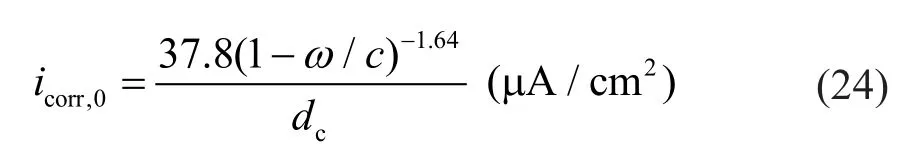
wheretpdenotes the time after corrosion initiation;icoor,0is the corrosion current density at the corrosion initiation time; andω/cis the water-cement ratio, which can be estimated from the Bolomey′s formula,

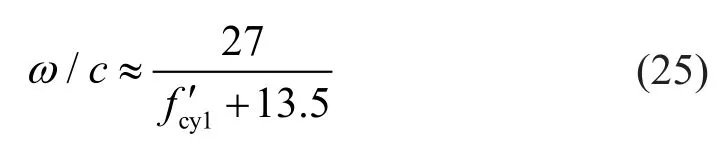
wheref′cy1is the concrete compressive strength of a standard test cylinder (MPa).

Under the effect of chloride corrosion, the diameters and yield strength of the reinforcing steels decrease with time.As indicated by Faraday′s law, the corrosion current density oficoor=1 μA/cm2corresponds to a corrosion penetration of 11.6 μm/year (Valet al., 1998).Thus, the reduction of the diameter of reinforcement at timetpcan be estimated by,

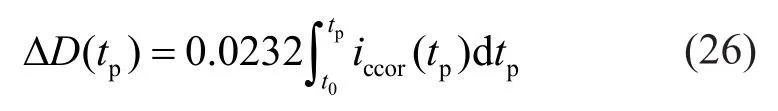
The time-dependent diameter of a corroding reinforcement (D(tp)) can be expressed as,

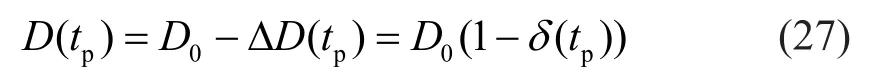
whereD0is the diameter of non-corroded reinforcements andδ(tp) denotes ΔD(tp)/D0.

Based on experimental studies, Duet al.(2005)proposed a time-varying yield strength model for the reinforcements under chloride corrosion,

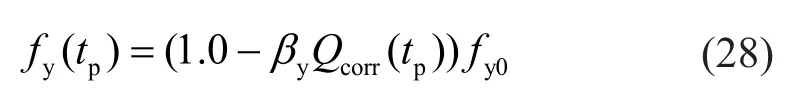
wherefy0is the yield strength of uncorroded rebars;βydenotes the reduction factor of yield strength, which is assumed to be 0.0012 for the ribbed bars; andQcoor(tp)is the corrosion degree of reinforcement (%) in terms of weight loss, which can be calculated by,

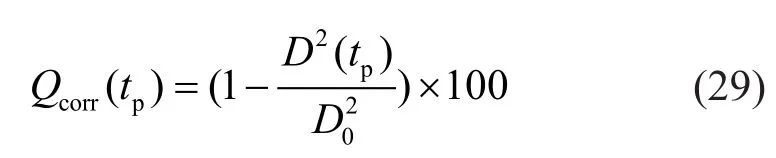
The corrosion products accumulated on the surface of reinforcing steels can lead to the cracking or spalling of the concrete cover.To properly assess the residual capacity of RC components during their lifecycle periods, the condition deterioration of concrete cover should also be considered.The time-dependent compressive strength of the corroded concrete cover(fc(tp)) can be estimated by (Vecchio and Collins, 1986),

wherefc0is the compressive strength of the intact concrete cover;Kis a coefficient related to the diameter and roughness of reinforcing bars and is commonly assumed to be 0.1 for the ribbed bars with medium-diameters(Capé, 1999);εc0is the strain at the peak compressive stress; andε1(tp) is the average tensile strain at timetpand can be calculated by,

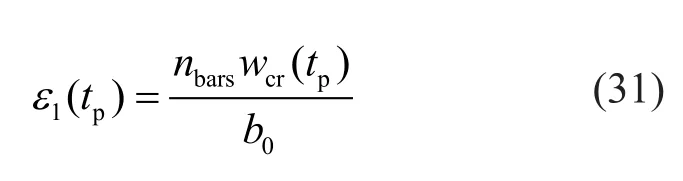
in whichb0is the cross-section width of the intact reinforced concrete component;nbarsis the number of reinforcing bars; andwcr(tp) denotes the mean crack width induced by each corroded bar at timetpand can be estimated by the following equations (Huang and Lee,2015),

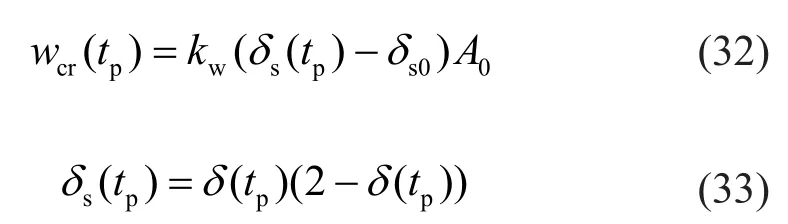
and

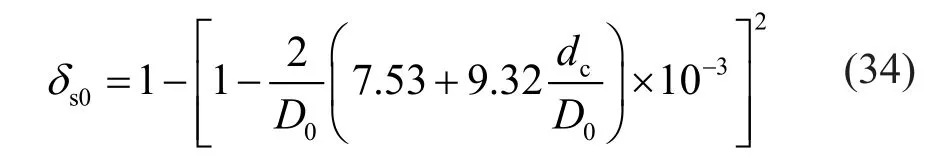
wherekwis a coefficient assumed to be 0.0575 mm-1;A0denotes the section area of the intact reinforcing bar;δs(tp) represents the degree of reinforcement corrosion at timetpandδs0is the corrosion degree corresponding to the cracking initiation of the concrete cover.

3 Case study of a bridge

To illustrate the feasibility of the proposed timedependent structural failure probability analysis methodology, a representative bridge model (Huang and Lee, 2015) is employed as an example.For simplicity,the RC bridge is modeled as a single-degree-of-freedom(SDOF).The elevation view, cross-section and the equivalent SDOF model of the bridge are shown in Fig.2.The time-varying stiffness and fundamental period of the equivalent SDOF system are calculated using the OpenSees platform (Mazzoniet al., 2005).The substructure is modeled with nonlinear beamcolumn elements with fiber sections.The OpenSees material type Concrete 01, Concrete 04, and Steel 02 are used to simulate the fibers of cover concrete, core concrete, and reinforcements, respectively.The nominal compressive strength of the concrete isfc0=28 MPa with strain valueεc0=0.22% and ultimate strain valueεcu=0.35%.The yield strength and elastic modulus of reinforcing steel are 420 MPa and 201 GPa, respectively.The superstructure weight per span length is 156 kN/m.Rigid links are employed to connect the SDOF model and the foundation, in other words, the soil-structure interaction effect is neglected in this study.

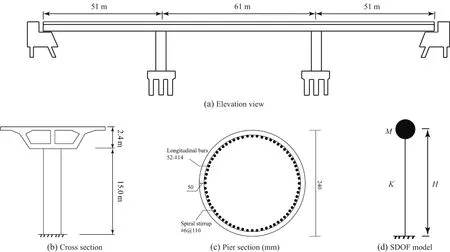
Fig.2 Elevation view, cross-section and the SDOF model of the bridge

To study the life-cycle failure probability of this example bridge, the influence of chloride corrosion onthe bridge columns is considered.Based on Eq.(22),the corrosion initiation time of reinforcements can be calculated using the Monte Carlo simulation (MCS)method.The probabilistic distribution of the parameters in Eq.(22) is listed in Table 1.The MCS result indicates that the reinforcement corrosion initiation time is compatible with a log-normal distribution with a mean of 15.2 years and a standard deviation of 7.92 years.The time after corrosion initiation is employed to calculate the reinforcement diameters, yield strengths and compressive strengths of concrete cover at every 15-year time step after reinforcement corrosion initiation based on the corrosion models introduced in Section 2.3.

Table 2 summarizes the calculated time-dependent fundamental periods and stiffness of the equivalent SDOF models.The lateral stiffness is calculated by the reciprocal of the lateral displacement, which is obtained by applying a unit horizontal force at the top of this pier model in the OpenSees platform.Due to the performance degradation of concrete and reinforcing steel materials,the stiffness of the SDOF model decreases and the structural period increases over time.The fundamental periods of the intact model and the corroded model at 75 years after corrosion initiation are, respectively, 1.02 s and 1.25 s, with an increase of 22.5%.

Table 1 Random variables related to the corrosion initiation time

4 Probability distribution of MH load effects

To calculate the MH load effects of the example bridge, the earthquake and strong wind models for three areas are employed, namely San Francisco, Memphis and St Paul in the USA.As pointed out by Ghosnet al.(2003), there are 600, 38 and 1 earthquake events in San Francisco, Memphis and St Paul, respectively,and the wind hazard risk in San Francisco is lower than those of Memphis and St Paul.The corrosion in reinforcements will cause the decrease in strength of the rebar and concrete as well as the cross-sectional area of reinforcements.Then, the structural stiffness will decrease due to the deterioration, which causes a largerlinear deformation against single/concurrent seismic and strong wind loads.In addition, the load effect denotes the deformation at the top of bridge piers under multiple hazards.

4.1 Seismic load effects

The horizontal displacement response of the SDOF model under seismic load is computed byΔe=MA/K.Here,Mis superstructure weight,Ais the horizontal design spectral response acceleration andKis the lateral stiffness of the SDOF model.According to the design specification of ASCE 7-10 (ASCE, 2010), the horizontal design spectral response acceleration is expressed as,

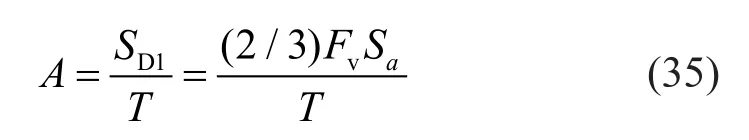
whereSD1is the design spectral response acceleration parameter at 1-s period,Tis the fundamental period of this bridge model,Fvis the long-period site coefficient andSais the spectral acceleration at the fundamental period.

The parametersMandKare assumed to be deterministic.Thus, the PDF ofΔecan be obtained by using the PDF ofSa.The seismic hazard function,H(x),is employed to quantify the occurrence probability of earthquakes at a certain site.H(x) is the probability of the spectral accelerationSagreater than or equal to a specific levelx, which can be estimated by (Cornell, 2002),

As discussed in Subsection 2.2, the occurrence of earthquakes at a certain area is modeled with a Poisson process, and the PDF of the spectral accelerationf(Sa)can be written as (Kameshwar and Padgett, 2014),

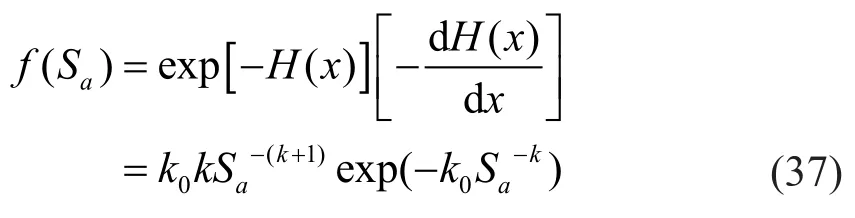
The approach to compute the parametersk0andkare summarized as follows: first, calculate the fundamental periods of the SDOF models at different corrosion scenarios; second, obtain the spectral accelerationsSa1andSa2at two hazard levels with exceedance probabilities of 10% and 2% in 50 years for the three areas accordingto the USGS seismic hazard curve; and finally, derive the values ofk0andkbased on Eq.(36) with two sets data ofH(x) andSa, whichare shown in Table 3.

Table 2 Characteristics of the SDOF model at different points in time

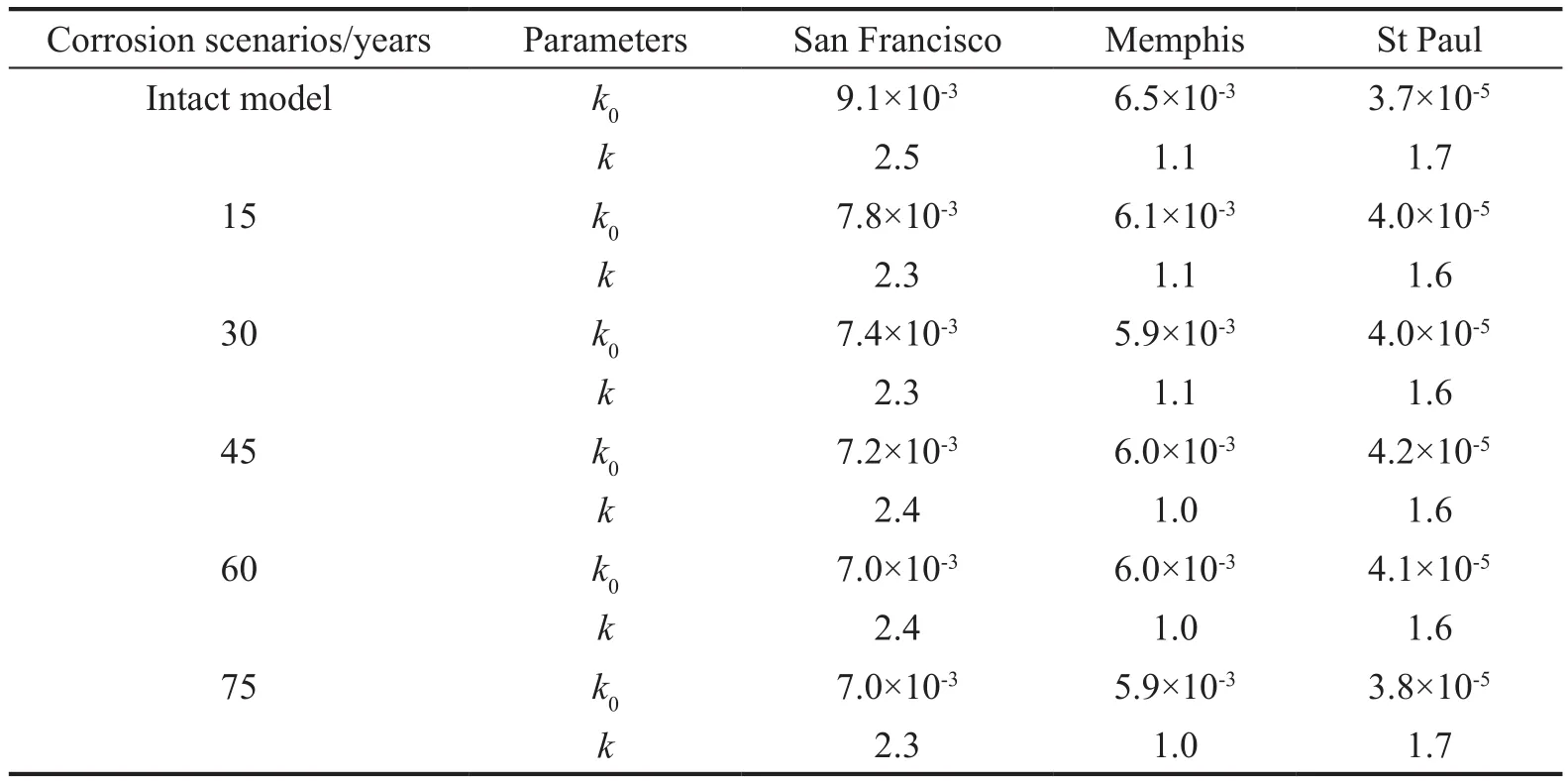
Table 3 Values of k0 and k for the SDOF models at different points in time

SinceΔe=MA/K, the cumulative probability function ofΔe, namely the probability ofΔeless than or equal to a certain value of intensityx,can be obtained by,

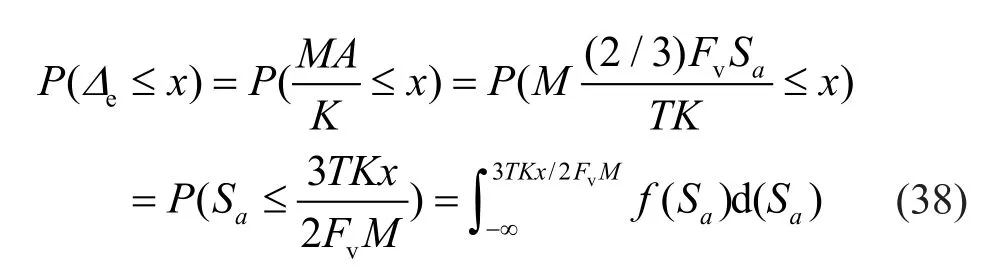
The probability density function ofΔe, namelyf(Δe),can be written as,

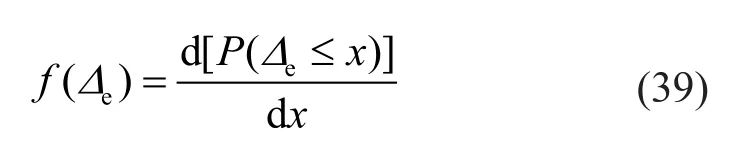
4.2 Strong wind load effects

The horizontal displacement response of the SDOF model subject to strong wind load is computed byΔw=FwS/K, in whichSis the projected area of the structure in the windward direction andFis the wind pressure.The wind pressure is calculated by (Vrouwenvelder, 2002),

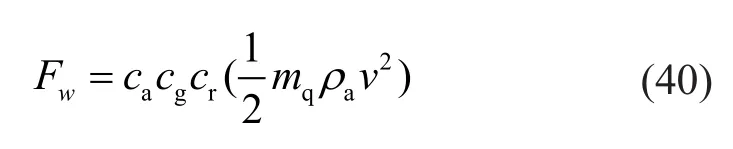
wherecais the aerodynamic shape factor;cgis the gust factor;cris the roughness factor;mqis the model factor;ρais the air density, andvis the basic design wind speed which can be derived from the design wind speed maps(ASCE, 2010).According to ASCE 7-10, the basic design wind speed is 52 m/s for San Francisco and 54 m/s for both Memphis and St Paul.

To develop the PDFs for the strong wind loadeffects, it is assumed that the strong wind speed follows the Gumbel distribution (Vrouwenvelder, 2002).The probabilistic distributions of each parameter in Eq.(40)are given in Table 4.In this study, the MCS method is employed to calculate the PDF of wind pressure.A convergence test is conducted and the results show that the mean and standard deviation of wind pressure is converged with a sample size of 50000.

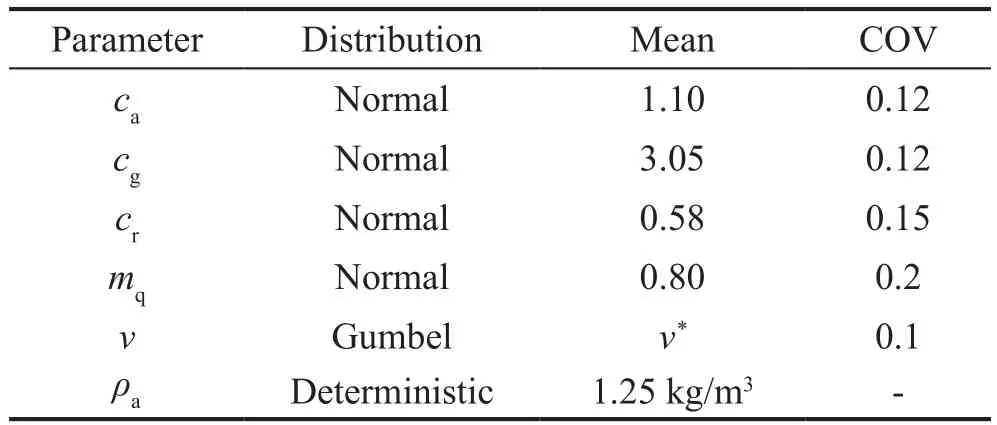
Table 4 Probabilistic distributions of parameters in Eq.(40)

The simulation results show that the probability distribution of wind pressure fits well with the lognormal distribution.The fitting results for the three areas are shown in Fig.3, in which the means and standard deviations of strong wind pressure are also illustrated.Then, the joint PDFs of the combined earthquake and strong wind load effects can be estimated based on Eq.(13).

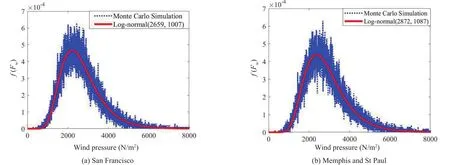
Fig.3 Comparison of MCS results and log-normal distribution

5 Numerical simulation results and discussions

To calculate the failure probability of the bridge under the multiple hazards of earthquakes and strong winds, some assumptions are made in this study.First,the annual occurrence rate of a strong wind is assumed to beλw=1/50 for the example bridge and the duration of each strong wind event is set to be 10 minutes (GB 50009-2012, 2012; Zhenget al., 2019a, 2019b).In addition, the annual occurrence rate of an earthquakeevent is assumed to beλe=2×10-3, which corresponds to the exceedance probabilities of 10% in 50 years as specified by the USGS hazard curve.Thus, the annual occurrence probabilities of the cases of only having an earthquake (Case I), simultaneously having an earthquake and a strong wind (Case II), and only having a strong wind (Case III) can be computed by Eqs.(17),(21) and (18), respectively.The occurrence probabilities of these cases are identical for the three areas of San Francisco, Memphis and St.Paul.The annual occurrence probabilities of Case I, II and III are 0.093, 3.45×10-8,and 0.907, respectively.However, the intensities of the earthquakes and strong winds are not the same for these three areas because the activity level of hazards for the three areas is different from one another (Ghosnet al., 2003).For example, the intensity of earthquake corresponds to the exceedance probabilities of 10% in 50 years of San Francisco is much higher than that of St.Paul, because San Francisco is more prone to earthquakes than St.Paul.In the calculation of time-dependent structural failure probability, the slight damage state of the example bridge is considered herein.The bridge is assumed to suffer slight damage if the drift ratio of the SDOF model is greater than 0.007 (Wen and Kang,2001a).Moreover, the probability density functions for the responses of the SDOF model at different corrosion scenarios under individual and concurrent earthquake and strong wind events can be easily obtained by the approach introduced in Section 4.

Based on Eqs.(10)-(12), the time-dependent conditional failure probabilities of the SDOF model under the hazard events of the three areas are calculated,as shown in Fig.4.It can be observed that the conditional failure probabilities of Case I is much higher than those of Case III for all three areas, implying that the structural damage induced by strong wind is slight as compared with that induced by the earthquake.Moreover, the conditional failure probability of Case II is higher than the summation of Cases I and III, indicating that simultaneous earthquakes and strong winds can resultin more severe structural damage than the individual hazards.This result is consistent with the study by Duthinh and Simiu (2009), which revealed that current design specifications are unwarranted for the structures located in regions exposed to the multiple hazards of earthquakes and strong winds.In addition, Figure 4 shows that the conditional failure probabilities of the SDOF model increase with time due to the effect of chloride-induced corrosion.However, the increasing trend for the time-dependent conditional failure probabilities of Case III is more obvious than those of the other two cases.These results indicate that the timedependent conditional failure probability of the example bridge is more sensitive to the strong wind hazard than the earthquake hazard.

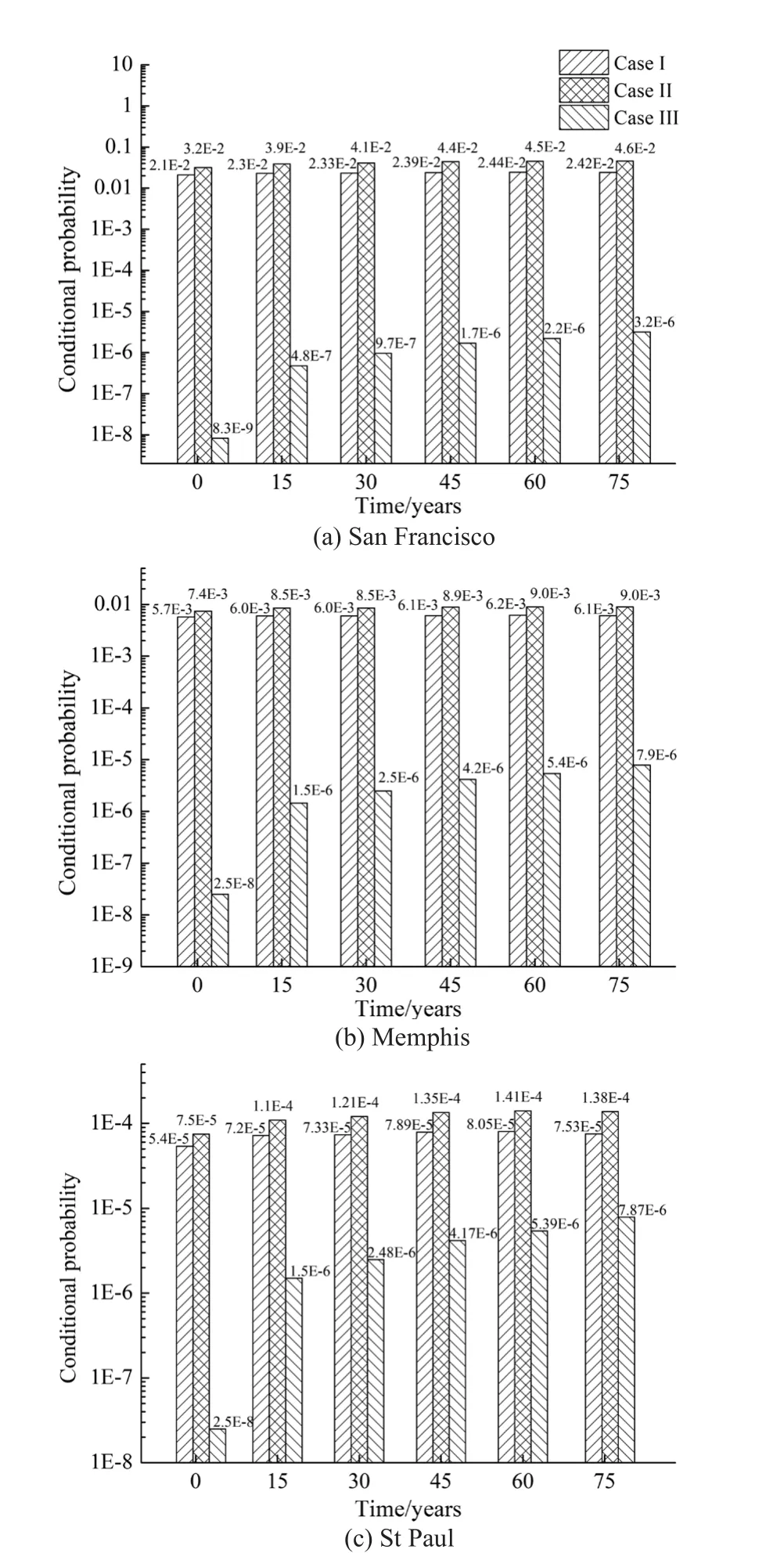
Fig.4 Time-dependent conditional failure probability of the SDOF model

The time-dependent failure probabilities (Pf),which can be calculated by multiplying the conditional failure probabilities with the occurrence probabilities of corresponding hazard events, are listed in Table 5.Letαdenotes the increasing extent of the failure probability of the corroded bridge model compared to that of the intact model.As shown in Table 5, the structural failure probabilities of San Francisco are higher than those of Memphis and St Paul.This is because the seismic hazard level of San Francisco is the highest among the three areas and the structural failure probability is dominated by earthquake events as discussed above.With the increase of time, the structural failure probability of the three areas all increases to different extents.Theαvalues for San Francisco and Memphis are much lower than those for St Paul.The difference is most likely because the structural failure in San Francisco and Memphis is mainly caused by earthquakes, however,both earthquakes and strong winds have significant effects on the structural failure probability of St Paul.Accordingly, the increasing extents of structural failure probability (αvalues) of St Paul are much higher than those of the other two areas because the time-dependent conditional failure probability of the example bridge is very sensitive to strong winds.

Table 5 Structural failure probabilities of the example bridge at different points in time

The contributions of different hazard cases to the total failure probability of the bridge in St Paul are shown in Fig.5.It can be observed that the contribution of Case II to the total failure probability can be neglected due to the low occurrence probability of concurrent earthquake and strong wind hazards.Moreover,along with the proceeding of chloride corrosion, the contribution of individual earthquake events (Case I) to the total probability decreases, while the contribution of individual strong wind events (Case III) increases.For the intact model, the contributions of the individual earthquakes and strong winds to the total structural failure probability are 95.5% and 0.5%, respectively.At 75 years after corrosion initiation, the contribution of strong wind increases to 50.6%, which is higher than that of the earthquake (49.4%).Thus, to achieve a more accurate lifecycle performance estimation of RC bridges under multiple hazards, the effect of chloride corrosion should be given special attention.Note that regularities of the time-dependent contributions of different hazards to the total probability in San Francisco and Memphis are similar to that for St Paul; therefore, they are not shown for conciseness.

Fig.5 Contributions of different hazard cases to the total structural failure probability of St Paul

The application of this study emphasizes that the contribution of the concurrent earthquake and strong wind hazards to the total failure probability of the example bridge is very small.Once earthquakes and strong winds occur simultaneously, the structural failure probability will significantly increase (as shown in Fig.4).In other words, the concurrent earthquakes and strong winds possess a significant potential threat to the safety of engineering structures.Therefore, the effect of multiple hazards should be comprehensively considered to achieve reasonable disaster resistance design of engineering structures.

6 Conclusions

This study presents a probabilistic method to analyze the life-cycle failure probabilities of RC bridges under the multiple hazards of earthquakes and strong winds.The influence of chloride-induced corrosion on the structural condition deterioration is emphasized.The time-dependent failure probability of a single-degreeof-freedom model is calculated by the proposed method.The main conclusions are summarized as follows:

1) Concurrent earthquakes and strong winds can result in much more severe structural damage than individual hazards.The conditional failure probability of the example bridge under simultaneously occurring earthquakes and strong winds are higher than the summation of those under individual hazards.

2) The contribution of concurrent earthquakes and strong winds to the total failure probability is very small due to the low probability of the simultaneous occurrence of these two hazards.However, it is suggested that the effect of multiple hazards should not be neglected because once the earthquake and strong wind events occur simultaneously, the structural failure probability may be significantly increased.

3) Due to the effect of chloride corrosion, the structural failure probability of this bridge under multiple hazards increases during the bridge′s lifetime.The contribution of each hazard event to the total probability at different corrosion scenarios is also influenced by chloride corrosion.

Note that the simplified SDOF model of the example bridge is used in this study to preliminarily investigate the effect of multiple hazards on the failure probabilities of deteriorated RC bridges.The nonlinear time-history analyses of detailed finite element models of long-span and flexible bridge structures, which are vulnerable to both earthquake and strong wind excitations, will be performed in future studies.In addition, the conclusions obtained by this current study may not be practical for general bridges.Nevertheless, the methodology proposed herein can provide a valuable reference for the life-cycle performance evaluation and design of RC bridges subject to multiple hazards.

Acknowledgement

This study is financially supported by the Fundamental Research Funds for the Central Universities(2021QN1022).