Seismic ground amplification induced by box-shaped tunnels

Damoon Feizi, Jafar Asgari Marnani, Hamid Alielahi and Mehdi Panji

1.Department of Civil Engineering, Faculty of Civil and Earth Resources Engineering, Central Tehran Branch,Islamic Azad University, Tehran, Iran

2.Department of Civil Engineering, Zanjan Branch, Islamic Azad University, Zanjan, Iran

Abstract: The growing use of underground structures, specifically to facilitate urban transportation, highlights the need to scrutinize the effects of such spaces on the seismic ground response as well as the surrounding buildings.In this regard,the seismic ground amplification variations in the vicinity of single and twin box-shaped tunnels subjected to SV waves have been investigated by the finite difference method.To evaluate the effects, generalizable dimensionless diagrams based on the results of parametric numerical analysis considering factors such as variations in the tunnels′ depth, the distances between the tunnels, tunnel lining flexibility, and input wave frequency, have been presented.In addition, to assess the effects of underground box-shaped tunnels on the response spectrum of the ground surface, seven selected accelerograms have been matched based on a specific design spectrum for the stiff soil condition of Eurocode 8 (CEN, 2006).The results underline the significant amplification effect of the box-shaped tunnels on the ground motions, specifically in the case of horizontal twin tunnels, which should be given more attention in current seismic design practices for surface structures.

Keywords: seismic amplification; box-shaped tunnels; response spectra; numerical method; parametric studies; buried depth

1 Introduction

Currently, underground transportation is a practical solution to the critical problem of traffic in metropolises,and regarding this, the construction of single and twin underground tunnels has been considered.One of the most critical issues related to underground tunnel construction is to investigate their effects on the seismic ground response and also their seismic amplification pattern during an earthquake.Note that most of the research conducted on this subject are analytical and numerical studies, along with a few empirical (Panzeraet al., 2013), local measurement (Sgarlatoet al., 2011),and physical modeling studies (Abuhajaret al., 2011,2015; Baziaret al., 2014; Abateet al., 2015; Baziaret al., 2016; Rabeti Moghadam and Baziar, 2016; Tsinidiset al., 2016).The majority of analytical studies are limited to the simple geometry of the tunnel and SH waves.Among the most important analytical studies are those conducted by Lee and Trifunac (1979), Lee(1988), Lee and Karl (1993), Leeet al.(1999, 2002,2004), Manoogian and Lee (1996), Manoogian (2000),Smerziniet al.(2008, 2009) and Liuet al.(2013, 2016).

On the other hand, the multidimensional nature of underground complications and limitations of the analytical and empirical methods highlight numerical methods to solve the wave scattering problem and evaluate the seismic ground response.The numerical methods used for seismic analysis of such sites can be divided into volume methods (e.g., finite element),boundary methods (e.g., boundary element), and hybrid methods.Among the first group, relevant numerical studies have been carried out by Crichlow (1982), who investigated the effects of the depth, size, shape, and position of underground tunnels and cavities on the seismic ground response using two-dimensional finite element modeling subjected to the vertical incident of SH waves.One of the most important numerical studies was conducted by Luco and De Barros (1994).These studies used the indirect boundary integral method, based on the two-dimensional Green′s functions for a viscoelastic half-space, to investigate the harmonic waves scattering induced by a buried, unlined, infinitely long cylindrical cavity of circular cross-section.To investigate the effects of underground structures on the surface seismic motion,Yiouta-Mitraet al.(2007) conducted a series of dynamic plane-strain numerical analyses based on the finite difference method to assess the effects of the soil medium characteristics, excitation frequency, tunnel diameter,depth of construction, and relative flexibility of the lining compared to that of the surrounding soil.In addition,Verrucciet al.(2012) performed a set of finite parametricanalyses to investigate the influence of a cavity on the ground motion at the surface of a homogeneous halfspace subjected to P and S waves.The size and depth of the cavity and the angle of the incidence of waves were varied to cover a wide range of real configurations.Alielahiet al.(2013, 2015), and Alielahi and Adampira(2016, 2018) studied the effects of single and twin tunnels on the seismic response of the ground surface using the boundary element method in the time-domain.The ground surface amplification patterns above single and twin underground tunnels were examined based on several effective parameters such as the wavelength of the incident wave, buried depth, and spacing distance of the twin tunnels.Note that few studies have been conducted on the dynamic interaction of tunnel-soilaboveground building systems in recent years (Abateet al., 2019).In this regard, Abate and Massimino (2017)analyzed the dynamic interaction that occurs between a tunnel, the soil, and an aboveground building for a case history of the Catania (Italy) underground network using full-coupled FEM modelling and also investigated the effects of the tunnel on the response of the soil and/or of the building and vice versa.Furthermore, Abate and Massimino (2017) investigated the seismic response of the underground network in Catania (Italy) by a FEM parametric analysis.The cross-section involved a fully-coupled tunnel-soil-aboveground building system.The depth of the tunnel, the position of the aboveground building with respect to the tunnel, and seismic inputs were varied.Two tunnel depths, two building positions, and thirty recorded accelerograms were adopted.Tsinidis (2018) investigated the effect of heavy buildings on the response of urban single and twin circular tunnels when subjected to severe ground seismic shaking in the transversal direction.For this purpose, a numerical parametric study was conducted on representative tunnel-soil buildings systems, employing the finite element code.Sunet al.(2019) performed a series of two-dimensional numerical analyses through the finite difference code dealing with the possible amplification of the Daikai station (Kobe, Japan) on the ground motions.The soil nonlinearity, the soil shear wave velocity, and the underground station dimensions were considered.Among the newest numerical studies, a paper by Alielahi and Feizi (2021) could be mentioned.This study deals with the soil-structure interaction induced by underground tunnels subjected to SV waves using the finite element method (FEM).To this end,the surface structures’ lateral displacement and drift due to the effects of several dimensionless parameters,including the tunnel depth, the surface distance between the structure and the tunnel, and the number of surface structure′s stories were investigated.Also, Shadabietal.(2022) investigated the role of cover material in cut and cover tunnels on the seismic response of the ground surface through the numerical approach.

Although previous studies revealed the significant effect of underground tunnels and cavities on the dynamic ground response, there are no comprehensive parametric studies related to the mentioned phenomenon for single and specifically twin box-shaped tunnels.On the other hand, reviewing the seismic design codes reveals that none of them addressed the effect of underground tunnels on the seismic ground response, and this effect has been overlooked in the seismic design of the surface structures.

This study investigates the seismic ground response in the presence of single and twin box-shaped tunnels in a viscoelastic half-space subjected to SV waves via parametric studies based on the finite difference method using FLAC 2D.Note that the relevant parameters, such as input wave frequency, depth, and distance ratio, were de-dimensionalized to make the results more practical.

2 Problem statement

The present study performed a parametric analysis related to the effect of the single and twin box-shaped underground tunnels in a viscoelastic half-space subjected to SV waves.To facilitate the classification of the results and make them generalizable for similar conditions, the relevant geometric and mechanical parameters were nondimensionalized.In this study, dimensionless geometric parameters include the surface distance ratio (x/a), the tunnel depth ratio (d/a), the distance between the tunnels(c/a), and dimensionless mechanical parameters, such as input wave frequency (η) and tunnel lining flexibility(J).The general geometry of the problem and the range of the dimensionless parameters are illustrated in Fig.1 and Table 1, respectively.

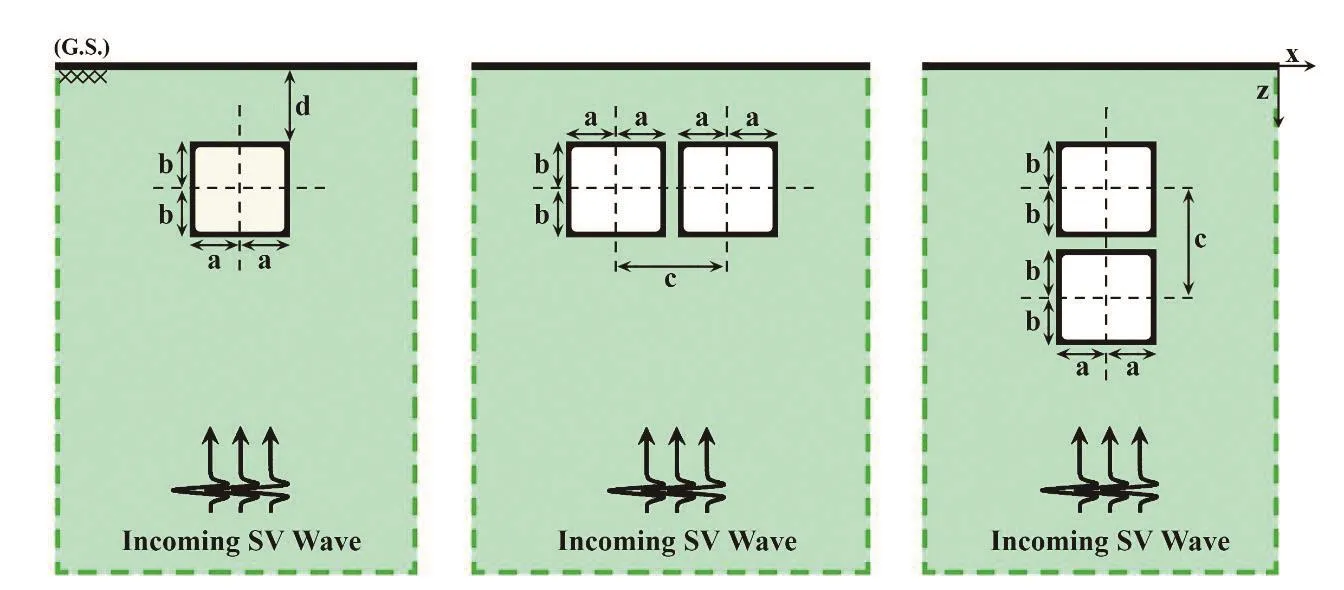
Fig.1 Model geometry and relevant parameters

Table 1 Dimensionless geometric and mechanical parameters

Note that the Ricker wavelet (Ricker, 1960) was used to apply the input motion in the dynamic analysis which is formulated as Eq.(1), wherefpis the dominant frequency,amaxrepresents the maximum time-history amplitude, andt0is the time at which the Ricker wavelet is at its peak.In this regard, the ground surface displacements in thex-zplane due to the SV wave have been investigated (Alielahi and Adampira, 2016).Furthermore, with defining the dimensionless frequency(η) as Eq.(2), the frequency content of the input wave was applied to the model, whereais the tunnel dimension,λis the incident wavelength,ωrepresents the angular frequency of the incident waves andc2indicates the shear wave velocity of the medium which has been considered a 400 m/s.Therefore, different values havebeen considered for dimensionless frequency to examine the low, mid and high responses.Moreover, by defining the relative flexibility of tunnel lining (J) as Eq.(3),proposed by Wang (1993), which indicates the ratio of lining stiffness to surrounding soil stiffness, the effect of the lining rigidity on the dynamic ground response was investigated.Note that whenJis lower than the unit, the lining rigidity of the structure is higher than the surrounding soil.In this case, the underground structure experienced lower degrees of deformation relative to the surrounding soil.On the other hand, the rigidity decreases with increasingJuntil this dimensionless parameter approaches infinity under the unlined tunnel scenario(Wang, 1993).In Eq.(3),GandEare, respectively,shear modulus of soil and plane strain elastic modulus of the frame,IRandIware moments of inertia per unit width for the slabs and walls, respectively.

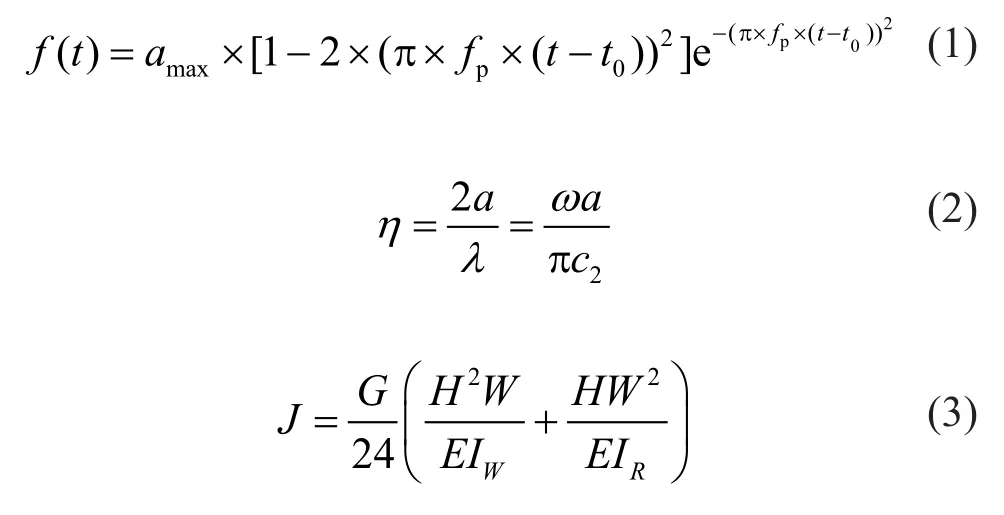
Moreover, the amplification values are obtained by dividing the Fourier response spectrum of the ground surface horizontal displacements in the presence of underground tunnels by the ground surface horizontal displacements under the free-field conditions.

3 Numerical simulation

Numerical models are mainly used to study the static and dynamic behavior of soil and structures as well as their interaction.Although laboratory models and analytical methods were preferred in the past by researchers, with the development of numerical methods and the increasing role of computers, numerical models have been gradually expanded for solving geotechnical problems such as the dynamic response analysis of soil-structure interaction.The finite difference method is regarded as almost the oldest numerical analysis technique in the literature, which is based on differential equations and takes initial and boundary values as input to the model.FLAC is an FDM-based software package capable of simulating the behavior of soil and rock as well as structures made of materials that may experience a plastic state at the point of failure.The medium and materials in this software are created and simulated by a number of elements forming a grid.Depending on the applied forces, boundary conditions of the problem,and the considered constitutive model, each element may exhibit a linear or nonlinear stress-strain behavior,and the materials may reach the point of failure and experience a plastic state, such that the grid may deform accordingly.

The numerical model is a finite difference grid with quadrilateral elements.The software automatically divides each of the elements into two triangular elements along which strain remains constant.In this study, the sizes of the elements were determined using dimension sensitivity analysis and by considering the velocity and frequency of the shear waves applied to the model and were selected to be sufficiently small to accurately simulate the propagation of the waves.To this end,as suggested by Kuhlemeyer and Lysmer (1973), the sizes of the elements were set to one-tenth of the shear wavelength propagated in the medium.Moreover, a viscoelastic constitutive model was considered for the problem, and the medium was assumed to be homogeneous and isotropic.Figure 2 reveals that the model (with dimensions of 500 m × 250 m) contains twin tunnels in the software.As previously mentioned,the dynamic loading was applied to the model through a Ricker wavelet.In the numerical simulation in FLAC,the dynamic loading was applied to the model boundaries as a stress time-history using the following relation for shear wave:

whereρis the density,Csrepresents the shear wave velocity, andVsis the velocity time-history of the Ricker wavelet.The factor of two in the above relation corresponds to the fact that half of the input energy is absorbed by the viscous boundary (Yiouta-Mitraet al.,2007).

Since the input earthquake load is applied to the model as stress, the bottom boundary should be modeled using a quiet boundary.To prevent errors caused by wave reflection towards inside the model from the side boundaries, free-field boundaries were used.Note that by considering the Rayleigh damping ratio of two percent, a viscoelastic model is taken into account.The basic form of a frequency-dependent Rayleigh damping matrix can be expressed as follows;

whereαandβare the mass-proportional and stiffnessproportional coefficients, respectively.The coefficients can be obtained according to the following equations:

whereωiandωjare the two parameters which ensure the frequency range,ξtaris the target damping ratio.ξis the damping ratio used in the calculations (Itasca, 2014).There are two important issues for the Rayleigh damping(Hu, 2006): (1) the choice of the type of damping model;and (2) the method to obtain three key parameters: the target damping ratioξtarand the matching frequencies.For the type of damping model, the simplified and full Rayleigh damping matrix are mainly used, the extended Rayleigh damping is seldom used in practice.With regard to the target damping ratio, which is always based on the small strain damping or on the smallest value to obtain a stable solution, a constant damping ratio range between 1.5% to 5% for geo-material is often employed(Sunet al., 2019).The liner structural element was used for tunnel lining modeling, and the interaction between this element and the surrounding soil was modeled using the Glued Interface that leads to a no sliding condition between these two environments (Itasca, 2014).

4 Numerical model verifications

Most seismic studies on box-shaped tunnels have been focused on the seismic performance of the structure itself and, therefore, there are a few studies regarding the effect of these structures on the seismic ground response.According to this, the validity and accuracy of the numerical model are compared with the results reported in the studies of Luco and De Barros (1994)and Yiouta-Mitraet al.(2007).As mentioned before,Luco and De Barros (1994) used the indirect boundary integral method based on the two-dimensional Green′s functions for a viscoelastic half-space to investigate the diffraction of harmonic plane waves by a buried,unlined, infinitely long cylindrical cavity.Their study presented the results by defining an amplification factor in which the displacement amplitude is normalized against the amplitude of the incident motion on the freefield ground surface.Figure 3 shows the verification of the numerical model for a specific case of the results,presented by Luco and De Barros (1994), where the depth ratio, dimensionless frequency, and lining stiffness areH/a=1.5,η=0.5, andJ=∞, respectively.

Furthermore, to investigate the effect of underground structures on surface seismic motion, Yiouta-Mitraet al.(2007) conducted a series of dynamic plane-strain numerical analyses, considering a circular tunnel embedded in a viscoelastic half-plane subjected to harmonic SV waves.The methodology of their study was based on the FDM, aiming to investigate the effects of soil medium characteristics, excitation frequency,tunnel diameter, buried depth, and the relative flexibility of the tunnel lining compared to the surrounding soil.To analyze the results, the amplification factor was obtained by dividing the Fourier spectrum of the horizontal displacement response of the ground surface in the presence of the tunnel by the free-field horizontal displacement amplitude.to consider tunnel lining in the current numerical model, the results reported by Yiouta-Mitraet al.(2007) for a specific case, a circular cavity with a lining stiffness ofJ=150, have been investigated.Figure 4 illustrates the verification result, where the depth ratio, dimensionless frequency, and lining stiffness areH/a=2,η=0.2, andJ=150, respectively.

5 Results and discussions

As mentioned earlier, the main objective of this parametric study is to investigate the dynamic ground response in the presence of single and twin box-shaped underground tunnels.To this end, the effect of the influential parameters, including the buried depth, the distance between the tunnels, the frequency content of excitation, and the tunnel lining flexibility, were studied for five considered geometric cases, including a single tunnel, integrated horizontal twin tunnels, separated horizontal twin tunnels, integrated vertical twin tunnels,and separated vertical twin tunnels.

5.1 Single box-shaped tunnel

In this section, the effect of the parameters involved in the problem is presented in the form of severaldiagrams.These figures reveal the combined effects of two or more parameters on the responses.The results of dynamic analyses show that the tunnel buried depth is one of the most important parameters affecting the responses.As depicted in Fig.5, within a range of-4＜x/a＜4, the amplification values have been obtained larger than one and, in the most critical case,d/a=0.5,the horizontal displacement of the ground surface has increased up to 1.7 due to the presence of the underground tunnel.The amplification pattern indicates that the responses at the symmetry axis are smaller than those at the sides of the tunnel, and the maximum amplification has occurred at the sides.In this regard,as the depth of the tunnel increases, the effects of the seismic amplification are decreased to a minimum, such that at depth ratios of 4 and 8, the surface amplification factor is reduced to 1, meaning that the presence of the tunnel does not affect the surface response at these depths.As the tunnel approaches the ground surface, the scattered waves are trapped in a smaller area, affecting the seismic ground response more intensely, and finally,the amplification values due to the presence of shallow and deep tunnels are entirely different from each other.Regarding the effect of the frequency content on the seismic ground amplification, the seismic analyses results are suggestive of the fact that this parameter is almost ineffective at |x/a|＞5, as illustrated in Fig.6.Assuming a tunnel with no lining atd/a=0.5, this figure indicates that the amplification factor is unique for the considered dimensionless frequencies.Note that in caseη=1.0, deamplification has occurred at -2＜x/a＜2,meaning that the presence of the underground tunnel hassignificantly reduced the horizontal displacements of the ground surface.Nevertheless, the most considerable seismic amplification has occurred at -3＜x/a＜3 for bothη=0.1 andη=2.0.In this regard, as illustrated in Fig.7, the frequency effect atd/a＜2.0 is more significant, and in the presence of a box-shaped tunnel, the minor responses, or in other words, deamplification, occurred atη=0.5.It is important to note that the responses are generally greater at 1≤x/a≤2, due to the wave scattering and shadow effect of the tunnel atx/a=0.It can be seen that the effect of frequency content on the amplification values due to the presence of shallow tunnels is more significant, and its variations are more complex.Moreover, the cross-section of the tunnel affects the pattern of amplification.In thisregard, the amplification pattern of a square underground tunnel is different from other tunnels (circular and horseshoe) and has two amplification peaks, especially in the shallow tunnels.In fact, the square shape creates high amplitude displacements due to the development of standing waves between the upper part of the cavity and the ground surface.Furthermore, the time required to dissipate these diffracted waves is longer than other crosssection shapes (Alielahi and Adampira, 2016).In the present study, such a phenomenon can also be observed in the results related to the effects of frequency content.In these cases, the two peaks of amplification values and bottom points between them (deamplification values)are distinguishable.There are intermediate frequencies(or intermediate periods) that the corresponding amplification values will be completely different from the higher and lower frequencies (or lower and higher periods).

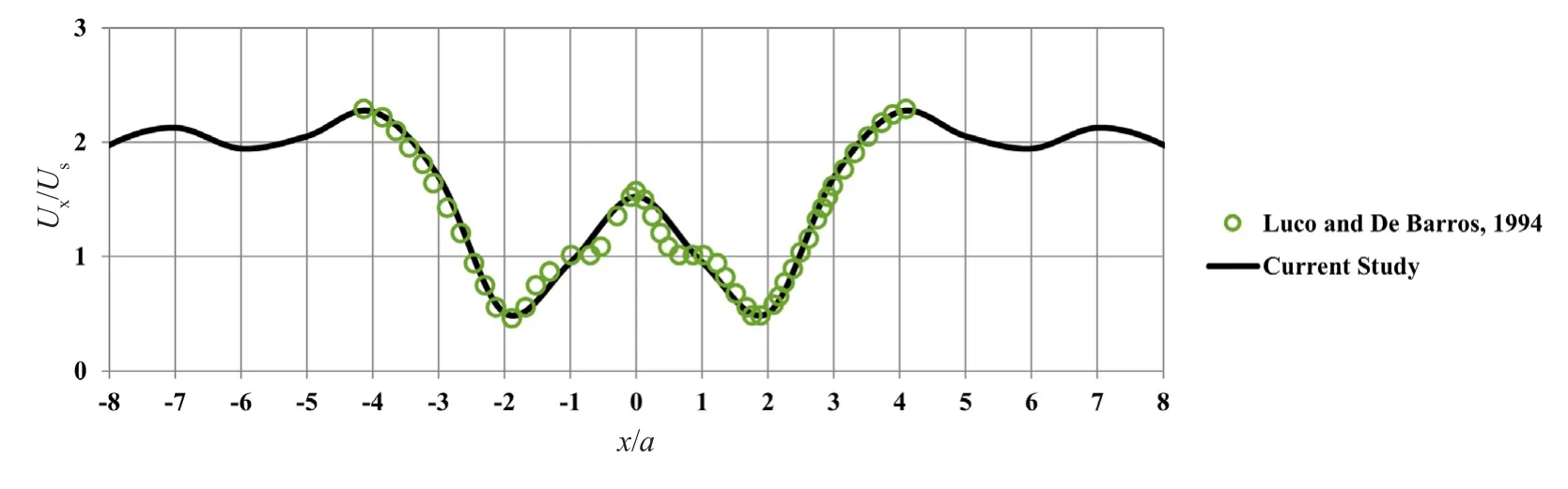
Fig.3 Comparison of the numerically computed normalized horizontal displacement on the ground surface, with the results of Luco and De Barros (1994).(H/a=1.5, η=0.5, and J=∞)

Fig.4 Comparison of the numerically computed normalized horizontal displacement on the ground surface, with the results of Yiouta-Mitra et al.(2007) (H/a=2.0, η=0.2, and J=150)

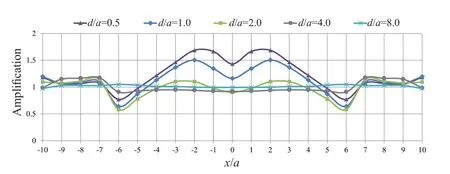
Fig.5 Variations of amplification factor in the presence of a box-shaped tunnel with depth ratio changes (η =0.1,ν =0.33, and J=∞)

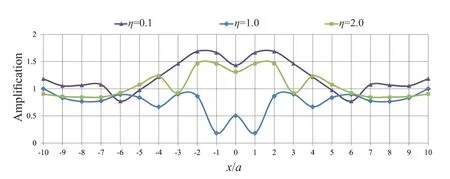
Fig.6 Variations of amplification factor in the presence of a box-shaped tunnel with frequency changes (d/a=0.5,ν =0.33, and J=∞)

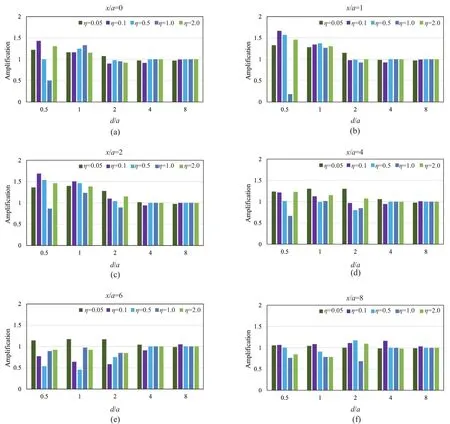
Fig.7 Variations of amplification values with frequency changes due to the single tunnel (J=∞)

To investigate the effect of the tunnel lining flexibility on the seismic amplification, three cases were considered, namely tunnels with no lining (J=∞),highly flexible lining (J=150) and relatively stiff lining(J=5).As illustrated in Fig.8, the effect of the tunnel lining on the seismic amplification can be investigated within two intervals.In the -6＜x/a＜6, the amplification factor is reduced in the presence of a lining and as the lining stiffness is increased.However, within the |x/a|＞6 interval, the effect of variations in this parameter on the amplification factor is almost negligible.Note that the intervals change depending on the depth ratio and dimensionless frequency.

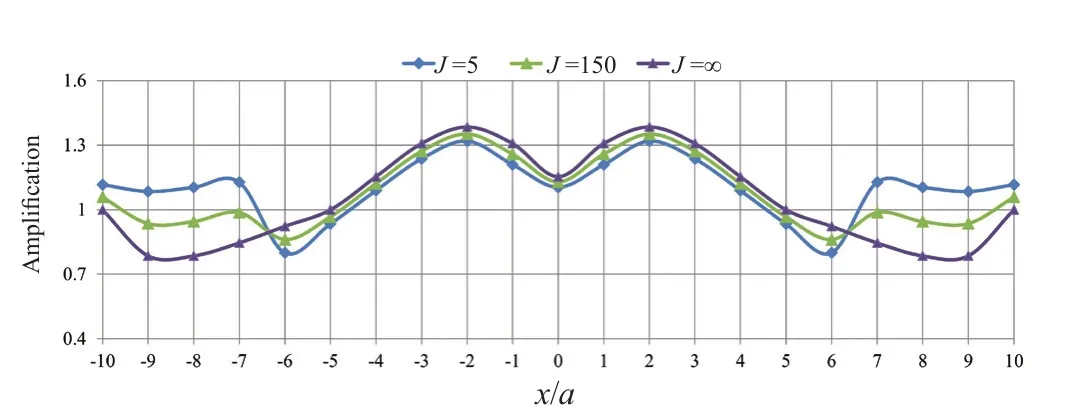
Fig.8 Variations of amplification factor in the presence of a box-shaped tunnel with lining flexibility changes(η=2.0, ν =0.33, and d/a=1.0)

5.2 Horizontal box-shaped tunnels

5.2.1 Integrated horizontal twin box-shaped tunnels

The effect of tunnel buried depth on the dynamic analysis results of the integrated horizontal twin box-shaped tunnels is shown in Fig.9.The largest amplification occurs within a range of -4＜x/a＜4 and, as the depth increases and the tunnel gets away from the ground surface, the amplification values are reduced to a minimum.Similar to the case for a single tunnel studied earlier, the responses at the symmetry axis of the tunnel are smaller than those at the sides, where the maximum amplification occurs as it gets away from the axis.Note that within the range |x/a|＞4, the horizontal displacement of the ground surface is significantly reduced, which is referred to as deamplification, due to the presence of the underground tunnel.Regarding the effect of the frequency content on the seismic ground amplification, as illustrated in Fig.10, the most critical results have occurred atη=0.1.The figure suggests that the response pattern atη=1.0 is different from the other dimensionless frequencies.In this case, the most significant amplifications have occurred at distances considerably farther from the tunnel axis.Furthermore,investigating the amplification pattern corresponding to the depth changes at different frequencies, as depicted in Fig.11, the amplification values atd/a≥1 are more significant, and the trend ofη=0.5 is different from other frequencies and is associated with deamplification.As the results indicate, the amplification patterns, in this case, are similar to the single tunnel, but the amplification values are higher due to the larger tunnel roof and wider trapped waves area.

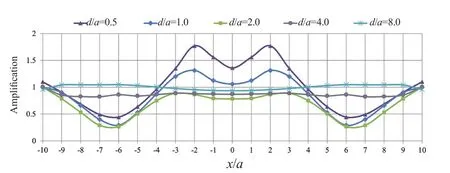
Fig.9 Variations of amplification factor in the presence of integrated horizontal twin box-shaped tunnels with depth ratio changes (η=0.1, ν =0.33, and J=∞)

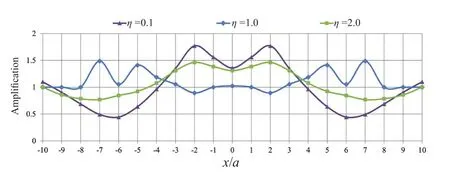
Fig.10 Variations of amplification factor in the presence of integrated horizontal twin box-shaped tunnels with frequency changes (d/a=0.5, ν =0.33, and J=∞)

Fig.11 Variations of amplification values with frequency changes due to the integrated horizontal twin tunnels (J=∞)

Regarding the effect of lining rigidity on the amplification pattern of integrated horizontal twin tunnels, as shown in Fig.12, as the lining rigidity increases, the amplification factor approaches 1, and the effect of underground space on the seismic ground response is reduced.These parameters should, more importantly, be studied at smaller buried depth ratios and, for instance, thicker and thus more rigid reinforced concrete linings play a more significant role in reducing the seismic ground displacements.

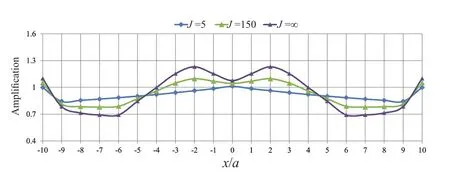
Fig.12 Variations of amplification factor in the presence of integrated horizontal twin tunnels with lining flexibility changes (η=2.0, ν =0.33, and d/a=1.0)

5.2.2 Separated horizontal twin box-shaped tunnels

In some real-world scenarios, box-shaped twin tunnels are not implemented in an integrated manner and maybe ultimately broken down into separate units depending on the project requirements.The dynamic analyses for this case were conducted by considering a relative center-to-center horizontal distance (c/a).As suggested by the results, the amplification factor is significantly increased in the presence of separated horizontal twin tunnels compared to the other cases, such that the horizontal displacements of the ground surface,compared to the free-field displacements, are increased up to three times atx/a=0.The close distance between the adjacent tunnels provides a space for entrapment and scattering of waves, significantly affecting the responses and indicating the importance of their consideration in the design of aboveground structures.According to Fig.13, in addition to the significant increase in the amplification factor, its pattern is also different from the other cases in the sense that the maximum amplification has occurred at the tunnel axis.Similar to other cases,as the buried depth increases, the amplification factor is decreased and atd/a＞2.0, the effect of the presenceof tunnels on the seismic ground response is almost negligible.Figure 14 illustrates the effect of different dimensionless frequencies on the amplification pattern of the seismic ground response in the existence of the separate horizontal twin tunnels.As shown, similar to other cases, the amplification patterns forη=0.1 andη=2.0 follow the same trend, which is completely different from that ofη=1.0.In this case, the seismic amplification of all the considered frequencies occurs within the range of -5＜x/a＜5, with its highest occurring atη=0.1 (up to three times and at the center of the tunnels), and its lowest atη=2.0 (up to two times and at the outer sides of the tunnel).In this regard, as illustrated in Fig.15, the amplification values at -4＜x/a＜4 andd/a＜2.0 are more considerable, and only atη=1.0 are the deamplification values observed.

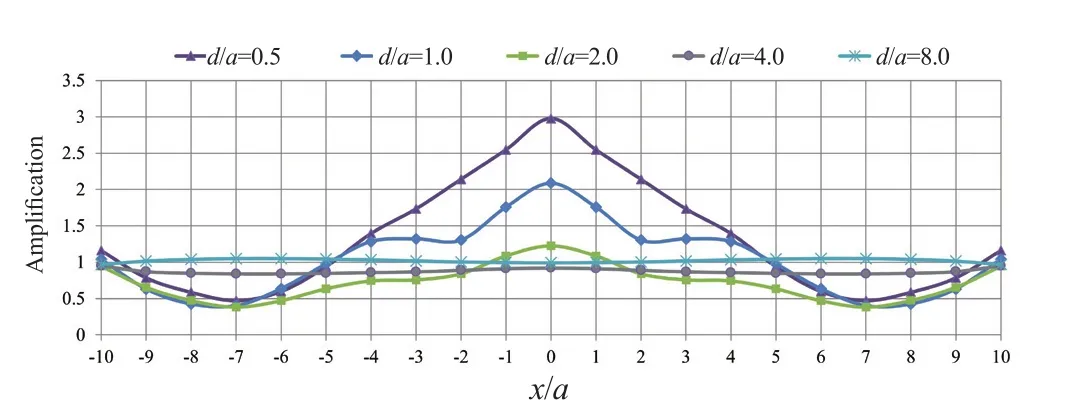
Fig.13 Variations of amplification factor in the presence of separated horizontal twin tunnels with depth ratio changes (η=0.1, ν =0.33, and J=∞)

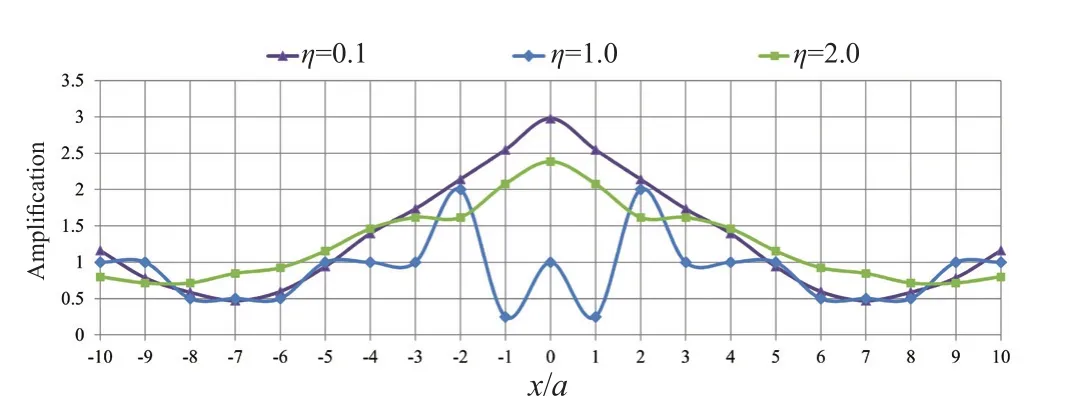
Fig.14 Variations of amplification factor in the presence of separated horizontal twin tunnels with frequency changes (d/a=0.5, ν =0.33, and J=∞)

Fig.15 Variations of amplification values with frequency changes due to the separated horizontal twin tunnels (J=∞)

As observed in Fig.16, regarding the tunnel lining,two different and fully separate ranges can be identified for the amplification pattern.Within the range -2＜x/a＜2, the most significant responses are associated with the tunnel with no lining, which the responses begin to decrease as the lining stiffness is increased.However, within|x/a|＞2, a significant range of seismic amplification,corresponding to the higher lining rigidity, has been obtained.This particular region of amplification pattern is exclusive to the presence of separated horizontal twin tunnels in which the amplification values are significantly larger at distances far from the tunnel axes compared to closer ones.

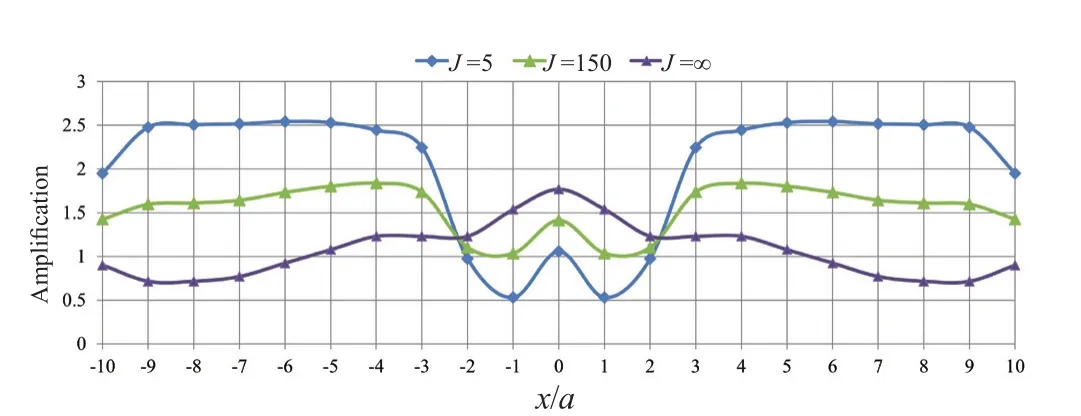
Fig.16 Variations of amplification factor in the presence of separated horizontal twin tunnels with lining flexibility changes (η=2, ν =0.33, and d/a=1.0)

5.3 Vertical box-shaped tunnels

5.3.1 Integrated vertical twin box-shaped tunnels

The scattering of SV waves was investigated in an underground rectangular space consisting of integrated vertical twin tunnels or multi-story underground transportation stations as a specific case of the considered geometry.As shown in Fig.17, regarding the seismic ground response, the amplification values,in this case, are smaller than the other studied cases, and even deamplification has occurred within a considerable range of the responses (|x/a|＞3).As the results reveal,the amplification patterns, in this case, are similar to the single tunnel, but the larger cross-section of the tunnel leads to smaller amplification values.Moreover, the results illustrated in Figs.18 and 19 indicate that the largest amplification values occur atη=0.05, 1.0 within the range of |x/a|＞2, whereas at other frequencies, it tends to one.In addition, in general, the amplification pattern atη=0.5 is different from the others and is generally associated with deamplification.It is necessary to mention that in other cases, the most critical responses occurred atη=0.1.

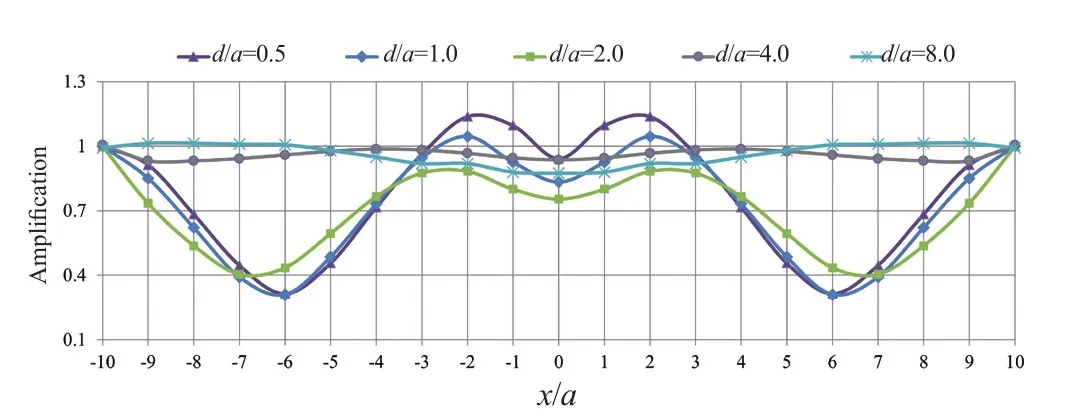
Fig.17 Variations of amplification factor in the presence of integrated vertical twin tunnels with depth ratio changes (η=0.1, ν =0.33, and J=∞)

Given that the amplification values, in this case, is smaller than that of the other cases, the effect of lining stiffness on the seismic ground response is significantly lower.Nevertheless, as observed in Fig.20, the amplification factor is decreased as the lining rigidity is increased.

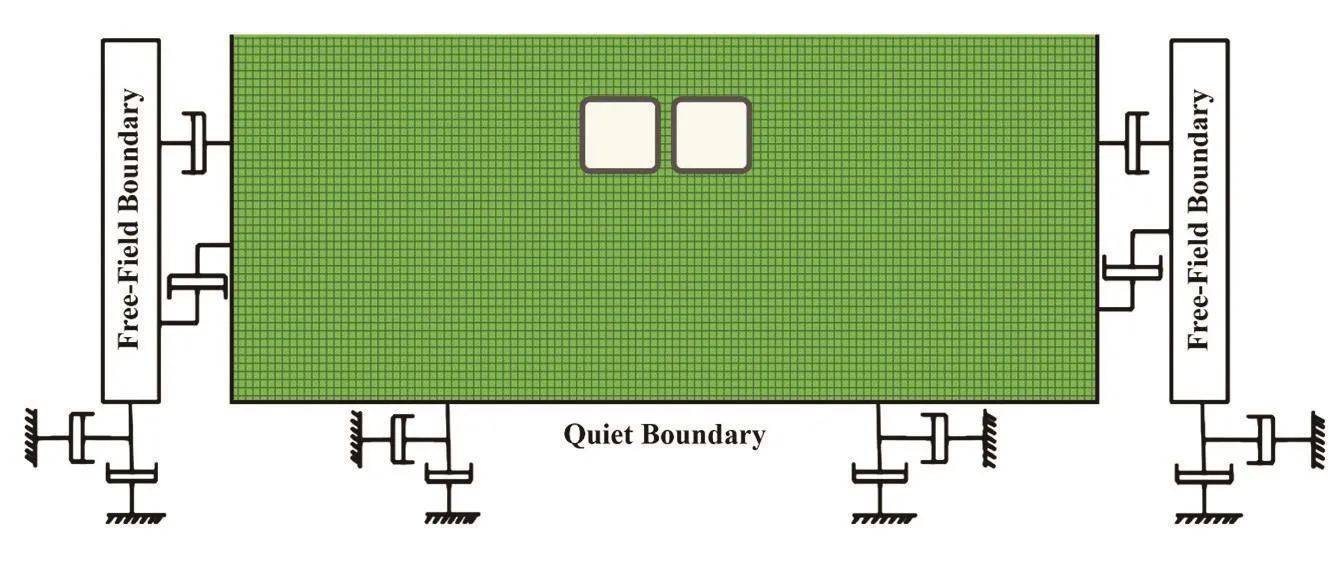
Fig.2 Numerical model

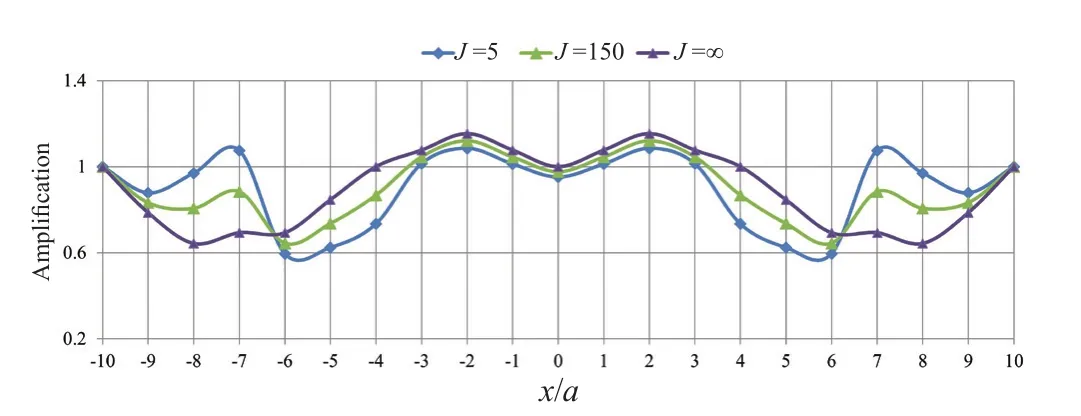
Fig.20 Variations of amplification factor in the presence of integrated vertical twin tunnels with lining flexibility changes (η=2.0, ν =0.33, and d/a=1.0)

5.3.2 Separated vertical twin box-shaped tunnels

In this configuration of twin underground tunnels,as illustrated in Fig.21, the amplification factor is decreased by increasing the buried depth, such that atd/a＜2.0, the effect of underground tunnels on the seismic ground response is almost negligible.Note that similar to the case of separated horizontal twin tunnels, the longitudinal distance between the tunnels increases the amplification values compared to the integrated case due to the entrapping and scattering of the propagated waves.Furthermore, the lower tunnel may play a protective role in isolating the SV waves leading to a considerable decrease of amplification values in comparison with the single tunnel.Regarding the effect of frequency content on the seismic ground amplification, as depicted in Figs.22 and 23, the most critical results have been obtained in the range of -4＜x/a＜4, due toη≤0.5 atd/a≤2.0.As the results show, the amplification values atd/a≤2.0 for other frequencies tend to one.Note that the amplification values at |x/a|＞4 induced byη=1.0 are different from the other frequencies, and larger amplification values are obtained.

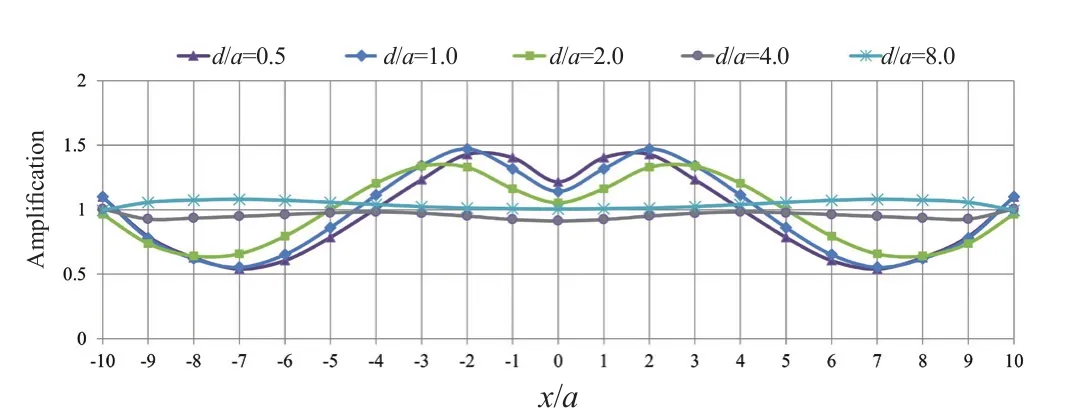
Fig.21 Variations of amplification factor in the presence of separated vertical twin tunnels with depth ratio changes (η=0.1, ν =0.33, and J=∞)

Regarding the effect of lining rigidity, as shown in Fig.24, two different ranges are distinguishable,including a significant range of the surface distance,i.e., -6＜x/a＜6, within which the effect of rigidity on the seismic ground response is almost negligible, and the range |x/a|＞6, within which the responses are amplified as the rigidity of the tunnel lining is increased.Thesame phenomenon is experienced by the single and the integrated vertical twin tunnels.In a broader sense, the results suggest that the effect of lining rigidity on the seismic amplification pattern of horizontal twin tunnels is significantly greater than that of the single and twin vertical tunnels.

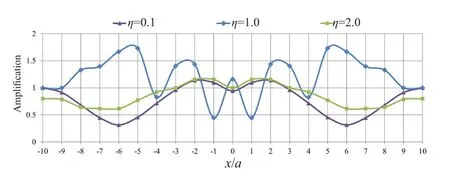
Fig.18 Variations of amplification factor in the presence of integrated vertical twin tunnels with frequency changes (d/a=0.5, ν =0.33, and J=∞)

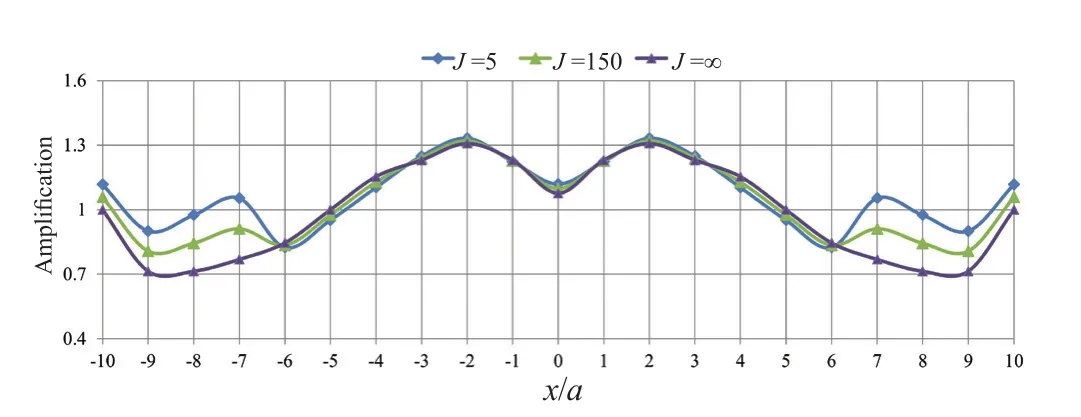
Fig.24 Variations of amplification factor in the presence of separated vertical twin tunnel with lining flexibility changes (η=2.0, ν =0.33, and d/a=1.0)

6 Practical aspects

The maximum seismic amplification is one of the key parameters to estimate the seismic behavior of the ground surface above underground structures.This parameter is usually applicable in the site responseanalysis for the seismic design of buildings and seismic microzonation studies.In this regard, the maximum amplification values of the ground surface located on the box-shaped tunnels versus the tunnel depth ratio (d/a) is presented.As can be seen in Fig.25, increasing the depth ratio decreases the maximum amplification factor.It is noteworthy that if the tunnel depth ratio increases to a value greater than four, the amplification potential at the ground surface would be less than about 10-20 percent.Moreover, the following simple equations approximate the maximum amplification values of the ground surface as a function of the tunnel depth ratio within the range 0.5≤d/a≤8.0.

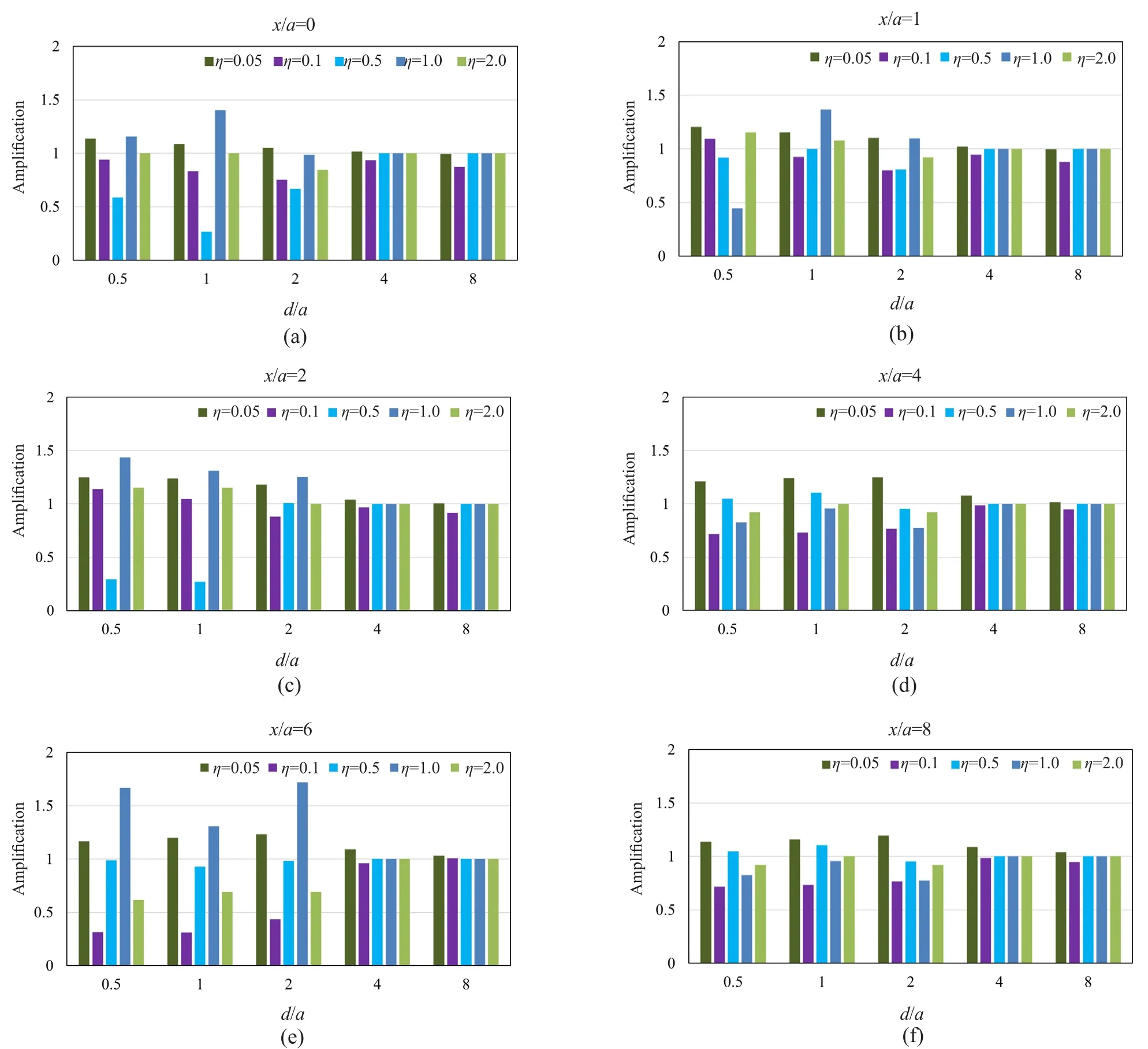
Fig.19 Variations of amplification values with frequency changes due to the integrated vertical twin tunnels (J=∞)

Fig.22 Variations of amplification factor in the presence of separated vertical twin tunnels with frequency changes (d/a=0.5, ν =0.33, and J=∞)

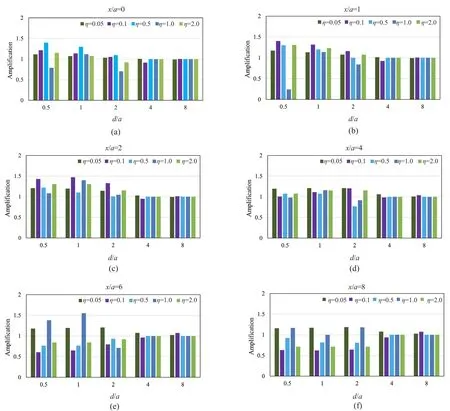
Fig.23 Variations of amplification values with frequency changes due to the separated vertical twin tunnels (J=∞)

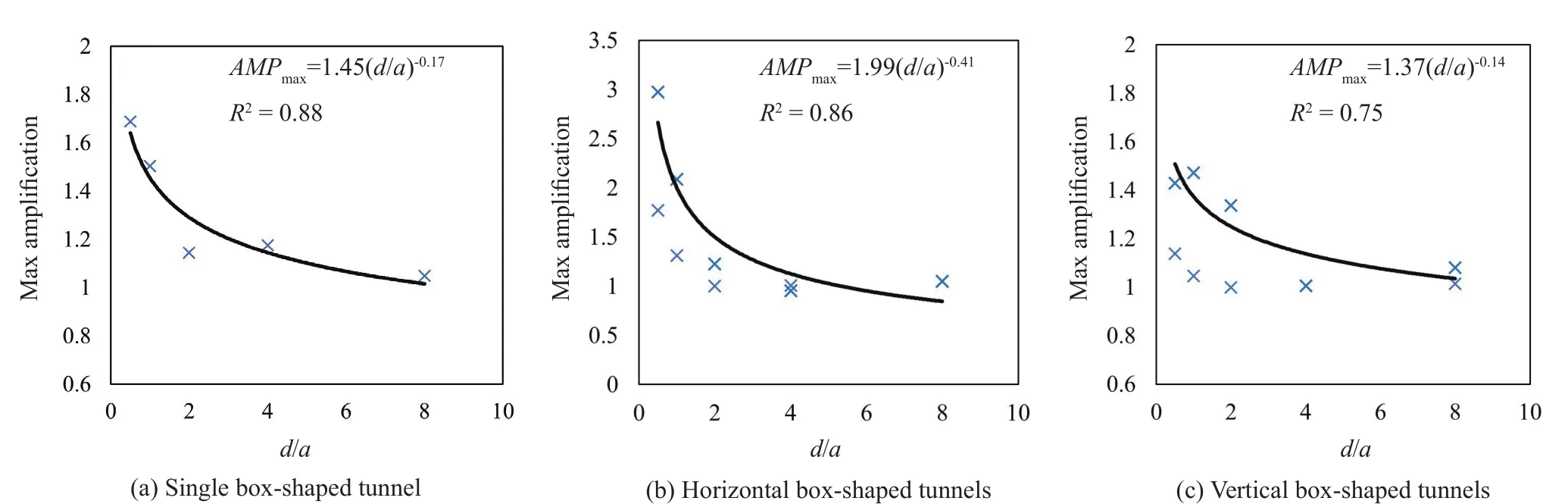
Fig.25 Maximum amplification factor at the ground surface via box-shaped tunnel depth ratio

7 Site-specific response spectra

In the previous sections, the seismic ground amplification patterns due to a Ricker wavelet have been illustrated.Since the response spectrum is composed of maximum responses of an SDOF structure with different frequencies, seven real earthquake accelerograms were selected from the Strong Motion Center (www.strongmotioncenter.org), reported in Table 2, to assess the effects of underground box-shaped tunnels on the response spectrum of the ground surface.Given the irregularity of the earthquake records and their different frequency contents, it is necessary to match the earthquake spectra with a specific design spectrum (e.g., design code spectrum) to obtain consistent, matching frequency contents.The matching of the ground motions has been performed using the wavelets algorithm proposed by Abrahamson (1992) and Hancocket al.(2006) based on stiff soil conditions (Type 1, Soil Class B andag=0.25 g)of Eurocode 8 (CEN, 2006) for each independent event.The target matching is applied for each scaled response spectrum for periods ranging from 0.1 to 4.0 s (Alielahi and Adampira, 2018).For instance, Fig.26 illustrates the spectral accelerations of the soil class B records before and after matching for the seven selected records.In Figs.27(a) to 27(g), the acceleration response spectrum of the ground surface versus the dimensionless period(defined as the inverse of the dimensionless frequency),for the seven considered matched accelerograms at the points with maximum amplification values on the ground surface (x/a=0and |x/a|=2), in the presence of a single underground box-shaped tunnel, integrated and separated horizontal twin tunnels as well as integrated and separated vertical twin tunnels are presented.The results indicate that the presence of shallow boxshaped tunnels has significant effects on the seismic ground response.Note that the presence of undergroundtwin tunnels leads to higher amplification values compared to the single tunnel.Moreover, among twin underground tunnels, the highest responses are related to separated horizontal twin tunnels because the close distance between the adjacent tunnels provides a space for entrapment and scattering of waves, and the lowest responses are related to separated vertical twin tunnels.In this regard, although the underground structures considerably affect the dimensionless period range of 5 to 20, this effect is almost negligible for dimensionless periods higher than 30.Note that amplification changes according to the type of underground structures and the periodic ranges affected reveal the same trend for all seven selected earthquakes.

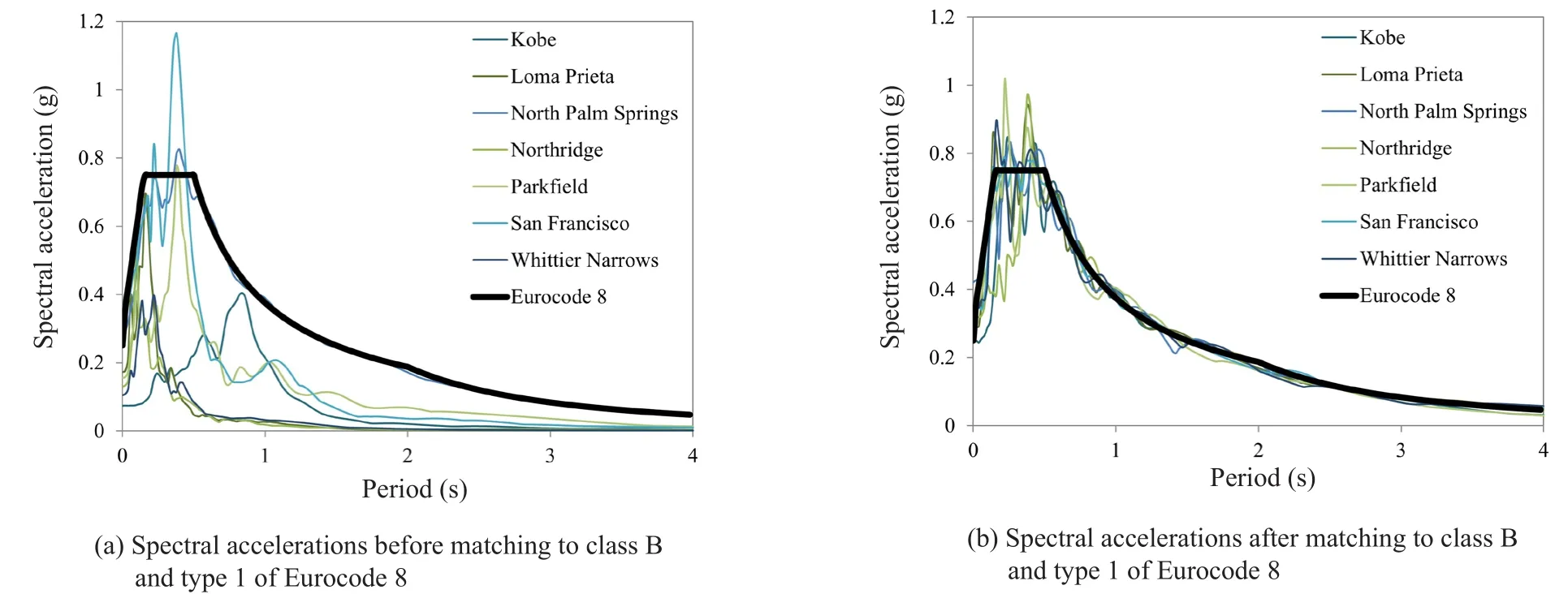
Fig.26 Matching the spectral accelerations of the soil class B records for the seven acceleration time histories (for 5% of critical damping)

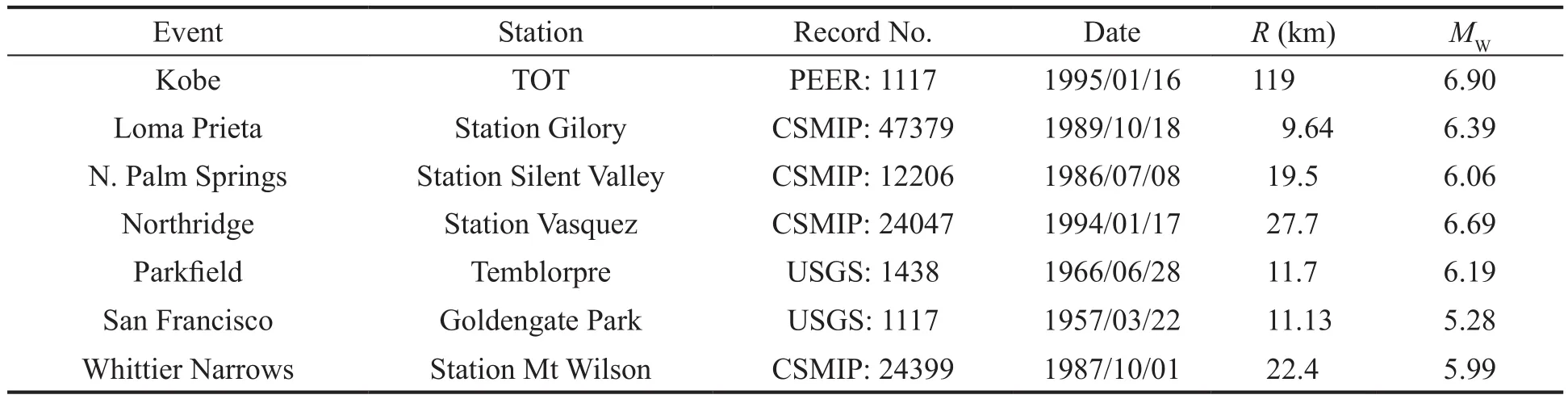
Table 2 Details about the selected earthquakes based on the site classification of class B in Eurocode 8 (CEN, 2006)

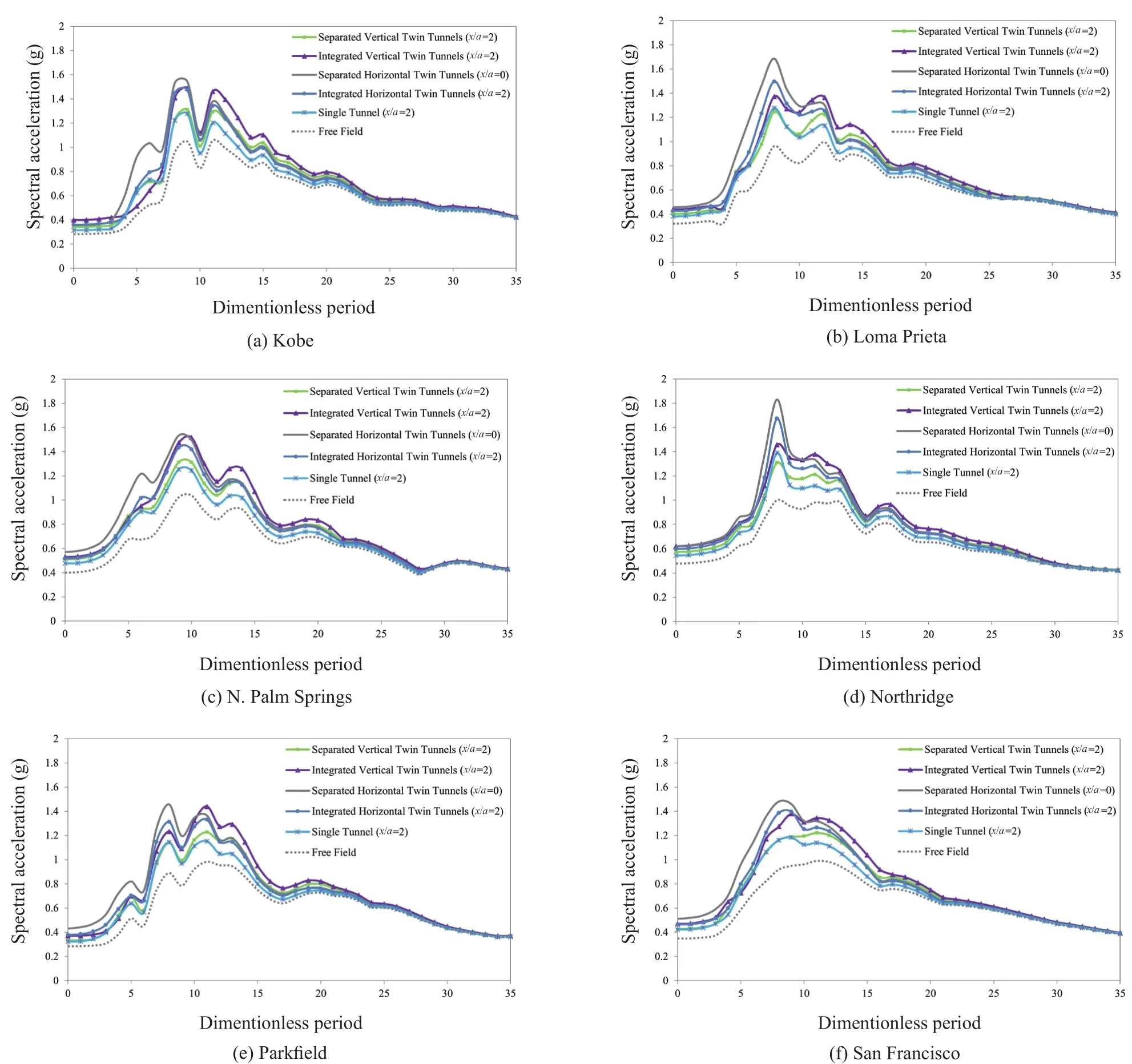
Fig.27 Site-specific response spectra for selected earthquakes in the presence of box-shaped tunnels (d/a=0.5, ν =0.33, and J=150)

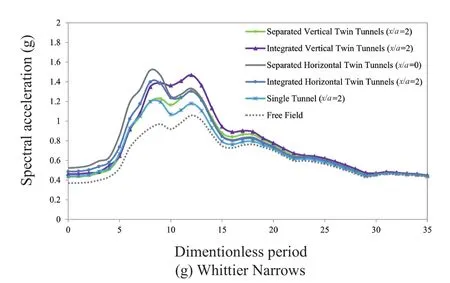
Fig.27 Continued

8 Concluding remarks

This study investigates seismic ground amplification variations in the vicinity of single and twin box-shaped tunnels in a viscoelastic half-space subjected to SV waves using the finite difference method.To this end,the effect of the influential parameters, including the tunnels’ depth, the distance between the tunnels, the frequency content of excitation, and tunnel lining rigidity were studied for five considered geometric cases.In this research, the amplification pattern at different depths has been studied first, and then the effect of dimensionless frequency and tunnel′s lining flexibility at shallow depths(more critical responses) has been investigated.Note that the viscoelastic behavior assumption can generate conservative responses in comparison with the nonlinear model, which can be reasonable given the uncertainties in estimating soil parameters and input excitation.Although using nonlinear models show more realistic soil behavior, especially in strong earthquakes and soft soils, their use can be limited due to the complexity and the number of relevant parameters in the amplification problems.The significant results of this study are summarized as follows:

1) The presence of single and twin box-shaped tunnels significantly affects the seismic ground response,such that the consequent seismic amplification pattern is a function of the changes in the important effective parameters such as the tunnel depth, the distance between the tunnels, the frequency content of excitation,and rigidity of the tunnel lining.

2) Among all the considered cases, the most critical seismic amplification values are due to the presence of separated horizontal twin tunnels, increasing the seismic ground response up to three times at some points.In this case, the close distance between the adjacent tunnels provides a space for entrapment and scattering of waves,significantly affecting the responses and indicating the importance of their consideration in the design of aboveground structures.On the other hand, the smallest responses were obtained in the presence of integrated vertical twin tunnels.Note that in this case, the larger cross-section of the tunnel and consequently the larger area of the scattered seismic wave as well as the absence of wave trapping space between the tunnels, resultsg in smaller amplification values.

3) In all the considered cases, as the depth ratio are increased, the effects of seismic ground amplification are reduced to a minimum, such that atd/a＞2.0, the amplification value is roughly 1, meaning that this seismic response is not affected by the presence of tunnels at the depth mentioned above.As the tunnel approaches the ground surface, the scattered waves are trapped in a smaller area, affecting the seismic ground response more intensely.

4) In the separated horizontal twin tunnels, the highest amplification value occurs at the center of the tunnel (|x/a|=0), whereas in other considered cases, it occurs at distances close to the sides of the tunnel.The longitudinal distance between the separated horizontal twin tunnels provides a space for entrapment and scattering waves, thus increasing the amplification value at the axis of tunnels.

5) In the separated vertical twin tunnels, the longitudinal distance between the tunnels increases the amplification values compared to the integrated case due to the entrapping and scattering of the propagated waves.Furthermore, the lower tunnel may play a protective role in isolating the SV waves leading to a considerable decrease of amplification values compared to thesingle tunnel.

6) Regarding the effect of the frequency content of excitation, the largest seismic ground amplifications related to the single and separated horizontal twin tunnels occur at a frequency ofη=0.1.However, in integrated horizontal twin tunnels as well as separated vertical twin tunnels, the most significant amplification values occur at the surface close to the center of the tunnels at a frequency ofη=0.1, whereas at farther surface distances,it occurs at a frequency ofη=1.0.Note that the largest amplification values related to the integrated vertical twin tunnels, occurring at a frequency ofη=1.0.From a general perspective, the amplification pattern associated with the frequency ofη=1.0 is different from that of other considered frequencies.

7) With regard to the effect of lining rigidity, two distinct regions can be observed, namely a region of the ground surface in the vicinity of the tunnels where the seismic amplification is reduced as the wall rigidity is increased, and a region located at surface distances farther from the location of tunnels where the responses are increased by increasing the tunnel lining rigidity.From a more general perspective, as the results suggest,the effect of the tunnel lining rigidity on the seismic amplification pattern of the horizontal twin tunnels is considerably more significant than that of the single and twin vertical tunnels.

8) The seismic response spectra of the ground surface in the presence of single and twin structures subjected to the seven considered earthquake records have been presented.The results indicate that the presence of shallow box-shaped tunnels and specifically twin tunnels can have a significant effect on the seismic ground amplification, such that this effect is more tangible within a period range of 5 to 20.

A review of the seismic design guidelines and manuals shows that the effect of the presence of underground spaces such as tunnels has not been considered in the seismic microzonation studies as well as the seismic design of superstructures, while the studies in the literature and also the present study are indicative of the considerable effect of subsurface spaces on the seismic amplification and surface displacements.