Vibration reduction analysis of new barriers in large model experiment

Ding Guangya, Shen Chenli, Wang Jun and Wu Ming

1.College of Civil Engineering and Architecture, Wenzhou University, Wenzhou 325035, China

2.School of Geological Engineering and Surveying, Chang’an University, Xi’an 710054, China

Abstract: A large model box was developed in our experiment to study the vibration reduction effect.Five hydraulic highperformance actuators are arranged in the upper part of the model box.There is a time difference between adjacent actuators,which can simulate the train induced vibration.To reduce vibration a composite barrier is designed; the barrier consists of a honeycomb concrete canvas and PE polymer water bags.The concrete canvas can be mixed with water to produce a hydration reaction to form a structure with a certain hardness.By simulating different train speeds and loads, vertical vibration velocity,and acceleration before and after the barrier are compared and analyzed.The experimental results show that the new barrier can achieve a good vibration reduction effect.When the simulated train speed increases, the damping effect of the barrier is improved.At a speed of 180 km/h, an amplitude of 1.5 m after the barrier is found to be 48.6% lower than that before the barrier.Velocity decreases by 24.2% at 36 km/h and by 38.1% at 108 km/h.

Keywords: vibration reduction; traffic loads; test; barrier; concrete canvas

1 Introduction

The rapid development of railway traffic brings with it environmental vibration problems.The vibration that is caused not only affects the daily life of residents,but also causes harm to surrounding buildings and precision instruments.In recent years, many experts and engineers at home and abroad have carried out several studies.Vibration isolation comes from a reduction of vibration source strength, blocking the vibration energy transmission path and vibration absorption by the vibration.Barrier vibration isolation is divided into active vibration isolation and passive vibration isolation,most of which is passive vibration isolation.The barrier is divided into a continuous barrier and a discontinuous barrier, depending on geometry.Continuous barriers generally include an open ditch that is filled with some types of filling material.Discontinuous barriers include row pile vibration isolation, honeycomb pile vibration isolation, and so on.

Trains, running along the ground, usually produce vibration.Yoshioka and Ashiya (1995) found that ground vibration frequency was mainly caused by the moving axle load.Krylov (1995) studied ground vibrations induced by superfast trains.He used a theoretical analysis to show that larger amplitudes of vibration are induced when train speed exceeds the Rayleigh wave velocity.Dieterman and Metrikine (1997) applied a simple harmonic load to the elastic cushion of a rigid foundation to study the critical velocity of a ballast system.Shenget al.(1999) considered the track to be two layers of a continuous elastic beam structure.Ground vibration response was analyzed by applying a simple harmonic load to a fixed point, a single harmonic load moving along the track direction, and a row of harmonic loads moving along the track direction.

In the process of reducing the vibration caused by a train′s operation, it was found that a filling ditch is an effective means for reducing road surface vibration caused by traffic load.Numerical simulations have been studied by many researchers.Shrivastava and Kameswara Rao (2002) used the finite element method(FEM) to investigate the vibration reduction effects of open and infilled trenches on transient Rayleigh waves.Yang and Hung (1997) used the finite/infinite element method to investigate the effectiveness of different vibration reduction measures to reduce vibration caused by train motion, such as the open trench, the infilled trench, and the elastic foundation.Lysmer and Waas(1972) used the FEM to assess the screening of trenches in layered soil by simulating boundary conditions.Gaoet al.(2006) and Caiet al.(2009) conducted theoretical and numerical studies on barrier damping and measured the vibration isolation efficiency of different barrier forms in saturated and unsaturated soil.

Many researchers have used experiments to study various wave barriers (Yanget al., 2020).Murilloet al.(2009) used indoor geotechnical centrifuge-scale experiments to investigate the reduction effectiveness of different sizes of foam-filled trenches.Haupt(1981) developed a model test by comparing open and concrete infilled trenches and concluded that isolation effectiveness is dependent on the depth of the trenches.Gaoet al.(2017) developed an improved threedimensional boundary element model to analyze the ground vibration isolation problem of a wave impedance block in saturated layered soil under a vertical load.Zoccaliet al.(2015) investigated the mitigation capacity of infilled trenches and the length influence on bound vibrations induced by trains.Stollwitzer and Fink (2020)analyzed the dynamic behavior of a ballast track using a large-scale test device with vertical loading.Alzawi and Hesham El Naggar (2011) conducted field experiments to investigate the protective performance of both open trenches and trenches infilled with GeoFoam material.In addition, they examined the influences of wall geometry and location on isolation efficiency.

In this paper, the vibration reduction effect of a filled groove barrier is analyzed utilizing theoretical research and experiments.A new type of vibration isolation device composed mainly of a honeycomb concrete canvas and a polyethylene (PE) and rubber water bag is proposed, and the influence of this new filling ditch barrier on environmental train vibration is analyzed.

2 Similitude rules

To simulate the prototype subgrade, elastic laws were applied for this test.Elastic scaling laws were determined according to Nakaharaet al.(2005).The following equilibrium equations are given:

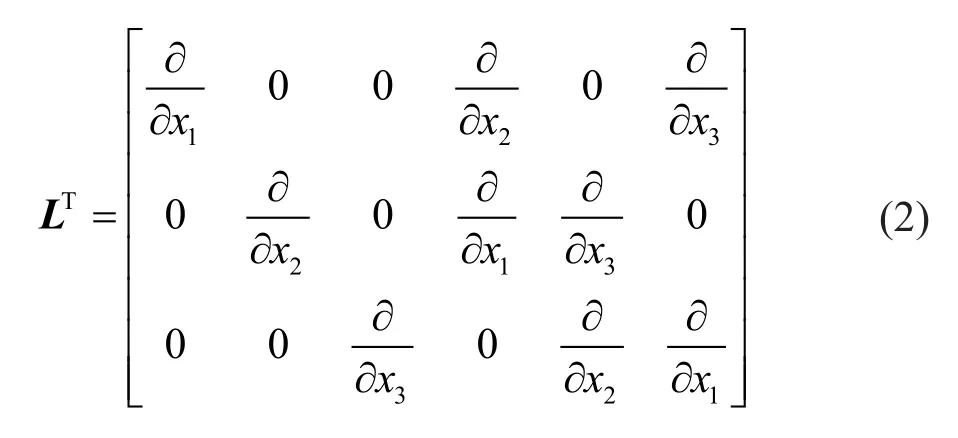
A quarter-reduced scale model was used in the test; other proportionality coefficients can be deduced based on the theory of similarity.Among them, the length involved in the model is 1/4 of the prototype, and acceleration is four times that of the prototype.

3 Test profiles

3.1 Model box and materials

The size of the model box was 6 m × 3 m × 4 m.From bottom to top there were 2 m of bottom sand layer,1 m of gravel ballast layer, 0.8 m of concrete slab, 0.3 m of a ballast layer, and 0.2 m of a sleeper rail structure.Thematerial and superstructure in the model box are shown in Fig.1 and Fig.2.The gradation of gravelly sands and fine sands is given in Table 1.

Table 1 Parameters of sands used for the subgrade

Fig.1 Three-dimensional schematic view of the model box

Fig.2 Various perspectives: (a) bottom sand stage, (b) gravel ballast layer stage, (c) subgrade concrete slab stage,(d) high imitation rail and (e) ballast side view of the vibrator

3.2 Vibration isolation material

The composite barrier consisted of a honeycomb concrete canvas and a PE polymer water bag.The interior of the concrete canvas was a mixture of threedimensional fabric and dry concrete, one side of which consisted of a polyvinyl chloride liner (waterproof layer).The new concrete canvas was mixed with water to produce a hydration reaction to form a structure with a certain degree of hardness.The concrete canvas was irrigated before the test, and the outer surface was set close to the surrounding gravel to improve the vibration isolation effect.The polymer PE bag was filled with water and the bag mouth tightened.The circumference of the bag was designed to be slightly smaller than the 6-sided honeycomb.The structure of the new barrier is shown in Fig.3.The property parameters of the concrete canvas are listed in Table 2.

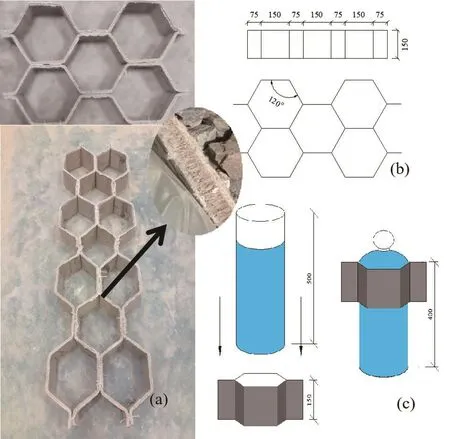
Fig.3 Structure diagram of new barriers

Table 2 Properties of the concrete canvas

3.3 Test equipment

The vibration isolation material was placed in the position shown in Fig.4(a).Three displacement tables(L1, L2, and L3) were installed on the surface of the roadbed for the duration of the vibration of the actuator,0.4 m from the concrete slab, at intervals of 0.2 m from the centre of the roadbed, respectively, to measure the vertical settlement.The adjacent vertical spacing between the three earth pressure sensors (P1, P2, and P3)was 0.5 m.The instrument arrangement is shown in Fig.4.To facilitate the operation of the instrument and at the same time have better observation of the large model box, a high-definition camera was mounted with a view of the model box, which was monitored in the control room.

Fig.4 Schematic diagram of sensor layout: (a) side view of sensor layout, (b) vibration pickup point

4 Test results and analysis

The experiment was carried out in the high-speed model box, at the upper end of five hydraulic actuators by setting adjacent time differences, to simulate different speeds.The time intervalΔtbetween two adjacent actuators in the track′s direction can be expressed as follows:

whereΔsis the distance between the neighbouring actuators andvis the train speed.Figure 5 shows the five waveforms of the different speeds used in this experiment (Bianet al., 2014).A full period of the M wave is given for each speed of 36 km/h, 72 km/h, 108 km/h,144 km/h and 180 km/h and shown in Figs.5(a), 5(b),5(c), 5(d), and 5(e), respectively.

4.1 Response analysis of velocity

The velocity response of each of the three measured points on the concrete base are shown in Fig.6.The V2and V3pickup points are in a symmetrical relationship.Measurements of the vibration speed are shown in Figs.6(a) and 6(b) under 5 kN and 15 kN dynamic loads,respectively.These results show that the higher the simulated speed, the greater the vibration speed.When the dynamic load is greater, the surface peak velocity is higher, and the peak velocity difference at different speeds is also higher.

The histograms show a comparison of the attenuation rate of the peak speed at different points V2, V3, and V1.It is evident that the attenuation rate increases with speed.It was found that the peak attenuation rate is higher when the dynamic load is small, but at low speeds, such as 36 km/h and 72 km/h, the velocity attenuation rate, as shown in Fig.6(a) and Fig.6(b), is similar.

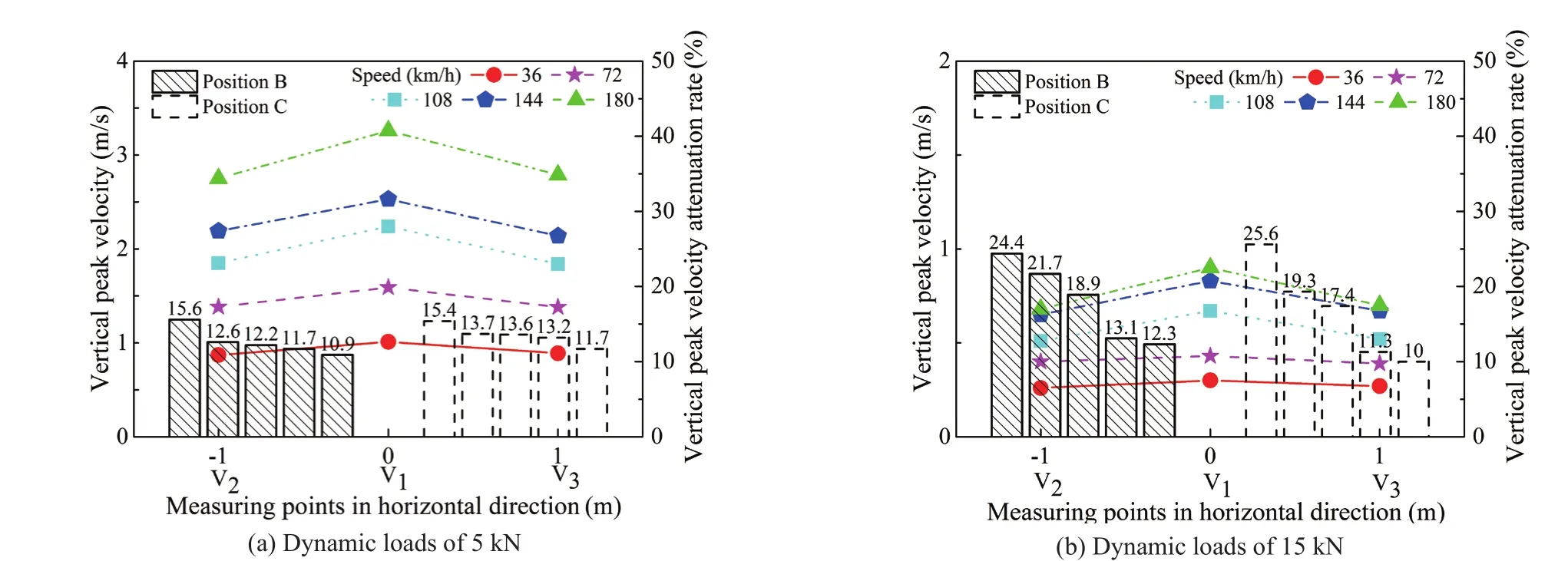
Fig.6 Speed response of road base at different speeds

Figure 7 shows the distribution of the peak velocity of the free field surface at different speeds.The abscissa(x-axis) in the figure indicates the horizontal direction and the ordinate (y-axis) indicates the vertical direction.Figure 7(a) shows a vertical view of the model device.Figures 7(b), 7(c), and 7(d) are contours for 180 km/h,108 km/h, and 36 km/h, respectively.The surface peak velocity in the free field increases as speed increases.The results show that the higher the speed, the greater the difference of peak-valley velocity in the free field.Simultaneously, peak velocity also significantly increases.

There is more than one wave produced by traffic vibration in the subgrade medium, such as P waves, Swaves, and R waves, which produce part of the reflective R wave and transmission R wave, and part of the P wave when they meet the new barrier.S waves cannot pass through media such as water.Liet al.(2015) found that when Rayleigh waves are incidental on the discontinuous medium, they are mainly propagated in the horizontal direction.The propagation of P waves is consistent with the direction of vibration, as shown in Fig.8.

Fig.8 Wave propagation schematic

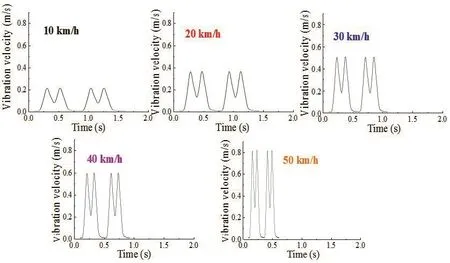
Fig.5 Waveform at 5 different speeds (single cycle)

Fig.7 Comparison of two-dimensional contours at different speeds: (a) vertical view of the model device, (b) train speed=180 km/h,(c) train speed=108 km/h, and (d) train speed=36 km/h

Figure 9 shows the variation trend of peak velocity with distance at the five different speeds with and without barrier vibration isolation at the V1jcentre.The red curves in the figure represent no barrier, and the blue curves represent the new type of vibration isolation structure, which combines concrete canvas with the PE and rubber water bags.With an increase in simulated speed, the surface peak velocity increases at different measuring points regardless of whether there is a barrier vibration structure.The test results show that the new isolation structure is highly effective in reducing road vibration and obviously limits the vibration response after the barrier.What also is worth mentioning is that at 180 km/h speed, the amplitude at the V15is reduced by 48.6% compared to the V11.

Figure 10 shows the variation distribution of vibration pickup amplitude at each measurement point in the model box.Figures 10(a), 10(b), 10(c), 10(d), and 10(e)are for speeds of 36 km/h, 72 km/h, 108 km/h, 144 km/h, and 180 km/h, respectively, all under moving loads of 15 kN.The red, blue, and black curves represent the variation in vibration amplitude of the measured points at V3j, V4j,and V1j, respectively.The discontinuous line segments represent the installation of the new barriers, and the continuous curves represent no barriers.Attention should be paid to the position of the V3jcolumn next to the isolation material and V31and V32close to the isolation barrier.As can be seen from the figure, regardless of speed, the black curves were always at the top, the blue in the middle, and the red at the bottom.When the speed was high, it was found that the blue curve points obviously increased, and a high-speed train has a great influence on the surrounding vibration.By observing the red curve, it can be concluded that when the speed is low, the amplitude of each measuring point of the barrier structure is much smaller than that without the barrier,and it is worth noting that there is no barrier in the front section of the V3jcolumn measuring points representing the red curve.Therefore, it can be concluded that when the speed is not high, the vibration reduction effect can still be achieved around the new barrier.

To illustrate the effect of the new vibration isolation structure, Fig.11 shows two three-dimensional contours,where the upper dynamic load is 15 kN, and the train speed is set at 180 km/h.Figure 11(a) represents the installation of the new type of vibration barrier, Fig.11(b)has no barrier installed.Figure 11 shows that at the right end of the figure, that is, in front of the barrier, the contours are all high amplitude, with little difference between them.At the left end, however, Fig.11(a) is basically in the blue state with the smaller amplitude, while Fig.11(b) shows yellowish green, and the amplitude isstill significant.These contours show that the new barrier has a good positive vibration isolation effect.

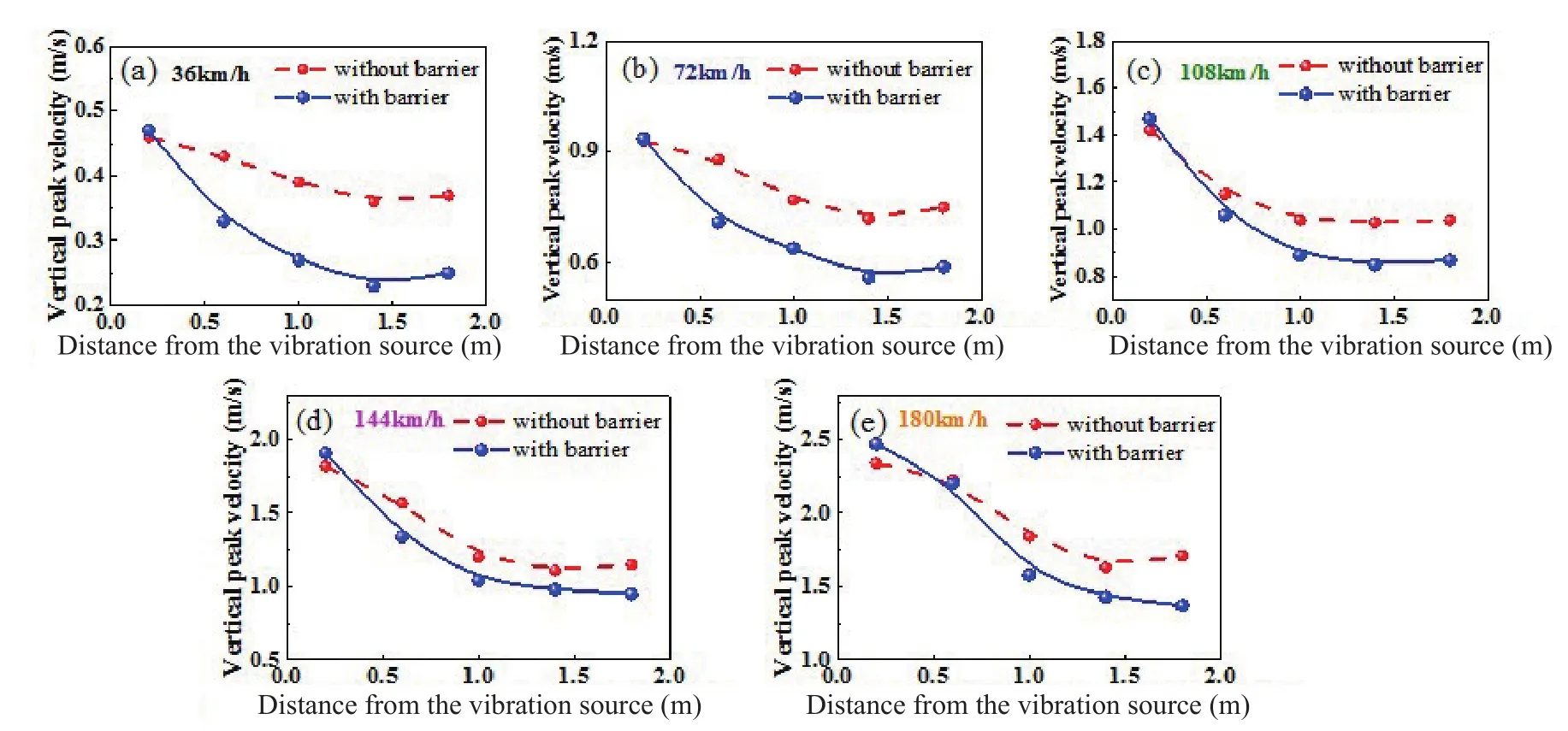
Fig.9 Barrier amplitude at different speeds: (a) train speed=36 km/h, (b) train speed=72 km/h, (c) train speed=108 km/h,(d) train speed=144 km/h, and (e) train speed=180 km/h

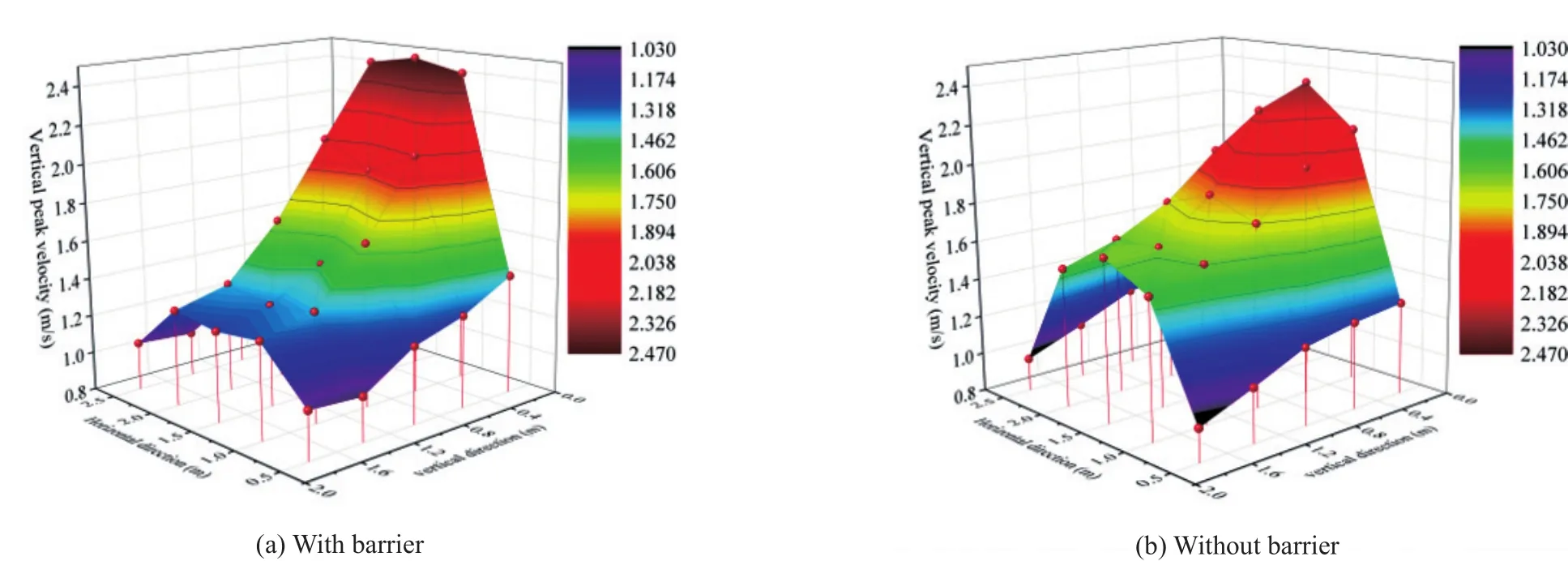
Fig.11 Comparison of 3D isoline maps at each point

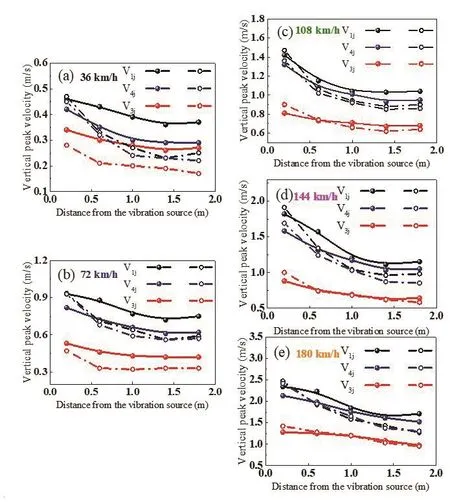
Fig.10 Amplitude of barrier at different speeds: (a) train speed=36 km/h, (b) train speed=72 km/h, (c) train speed=108 km/h,(d) train speed=144 km/h, and (e) train speed=180 km/h

Figure 12(a) compares the time history curves of the measured points at speeds of 36 km/h, 108 km/h and 180 km/h of the simulated train after installing the new barrier.Black represents the measured points at V11in front of the barrier, and red represents the measured points at V15at the back end of the barrier.To facilitate analysis and comparison, the time history signals for the same period were selected, from top to bottom, at 180 km/h, 108 km/h and 36 km/h.The higher the speed,respectively, 1.2 m/s, 0.56 m/s, and 0.23 m/s, the denser the corresponding time history curve, and the greater the difference between the corresponding measuring points.Moreover, Fig.12(b) shows a comparison of the amplitude of the whole area measuring points, at 180 km/h,108 km/h, and 36 km/h speed.The influence of speed on vibration is significant, and the attenuation rates of the measuring points for speeds 180 km/h, 108 km/h, and 36 km/h from V11to V15were 48.6%, 38.1%, and 24.2%,respectively.Meanwhile, it was found that the higher the speed, the greater the difference between the V1jcurve between the point line segment of the V3jposition and the centre position, which also shows that the new barrier structure plays a role in reducing the surrounding vibration.The greater the speed, the more obvious the vibration reduction effect.

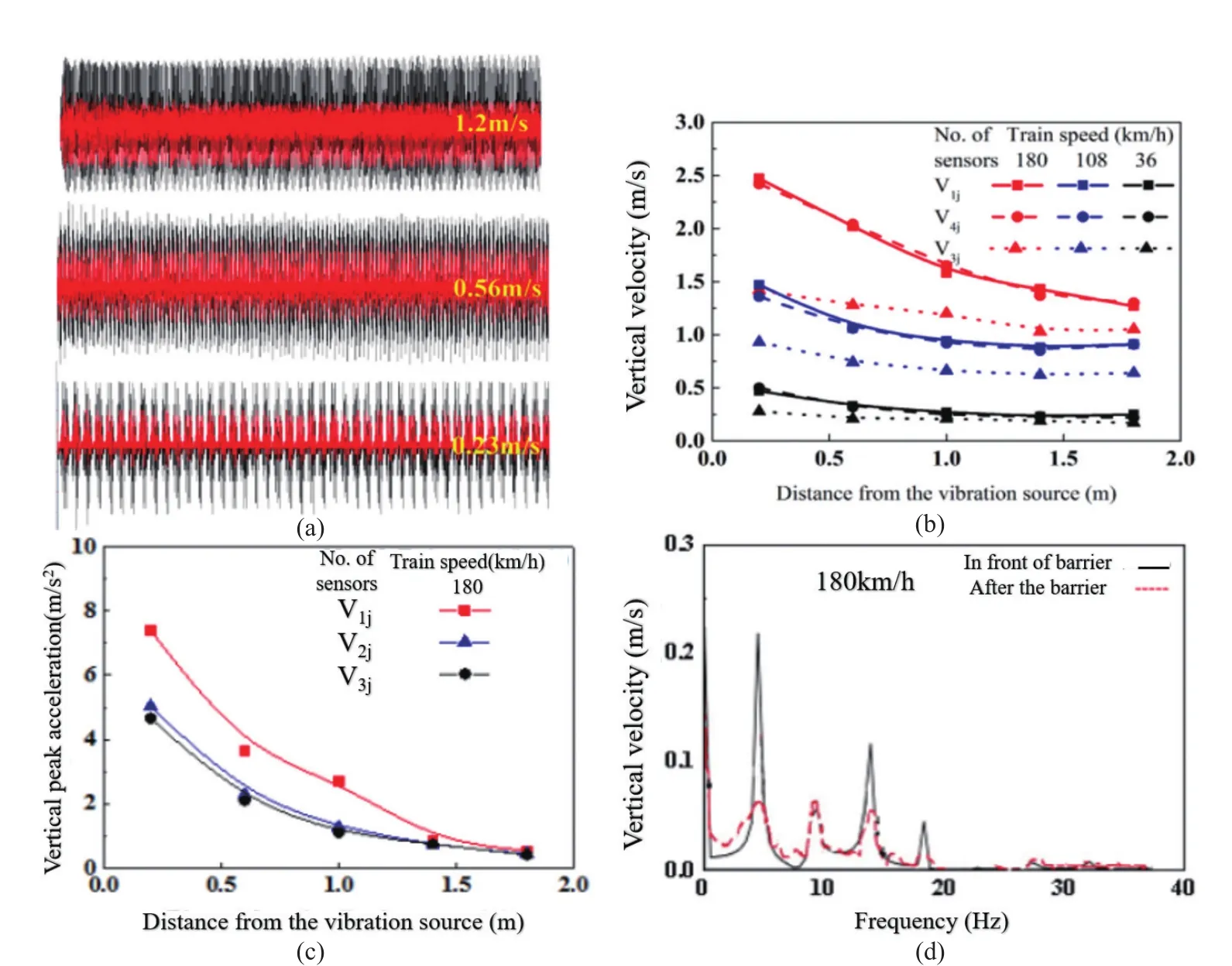
Fig.12 (a) Peak velocity time course, (b) peak velocities at different speeds, (c) peak acceleration versus distance from the vibration source, and (d) velocity versus frequency before and after the barrier

Figure 12(c) compares the peak acceleration of the whole spatial measurement point of the simulated train at 180 km/h, in which the V1jis located at the center and V2jand V3jare located on both sides and are symmetrical.We find that the acceleration attenuation is obvious, and the attenuation rate is larger than that for both sides.

Figure 12(d) plots vertical velocity versus frequency,given at a simulated train speed of 180 km/h.The black solid line represents the frequency response before the barrier and the red dashed line represents the frequency response after the barrier.Overall frequency can be reduced after the barrier, and the main frequency is obviously reduced.

4.2 Mechanism analysis

The vibration amplitude reduction ratio (Arr) was introduced into our tests, following Woods (1968).The effect of vibration reduction was evaluated by comparing the amplitude of vibration with and without barriers.The specific equations are as follows:

where the numerator represents the amplitude of the vertical vibration under the barrier and the denominator represents the amplitude without the barrier.

Figure 13 shows the distribution ofArrat the V1jcolumn for speeds of 180 km/h, 108 km/h, and 36 km/h.The black, blue, and red line segments represent theArrdistribution of the V1j, V4jand V3jcolumn points,respectively.At different speeds, there are three profiles ofArrand distance.Only at the Vi1of the first measuring point in front of the barrier is theArrvalue greater than 1.The front end of the new barrier does have a slight amplitude amplification when the speed is high and theArrvalue changes slowly.At the same time, as the distance increases, the value of theArralso shows a decreasing trend, which indicates that the new barrier structure is suitable for the road at the higher speed and for a longer distance.A thin foam plate was pasted on one end wall of the model box prior to the test to absorb the rebound of the wave, but the metal material comprising the wall of the model box was more rigid so that the wave was not completely absorbed.Therefore, at the Vi5point of the last measurement point, theArrvalue of these three pictures does not change much or even slightly increases compared to the previous measurement point.

We define the overall damping ratioto judge the overall damping performance of the vibration isolation material.The equation is as follows:

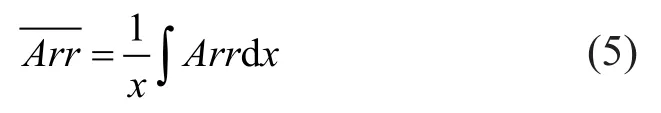
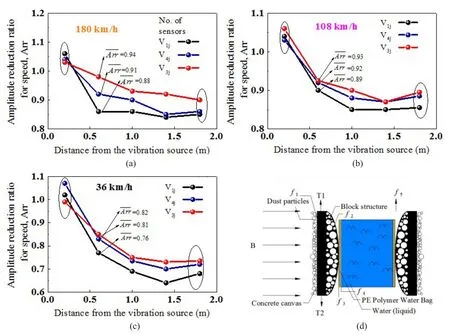
Fig.13values of the barrier under different speeds at the measuring point.(a) train speed=180 km/h, (b) train speed=108 km/h, (c) train speed=36 km/h, and (d) damping mechanism of the barrier

Figure 13 also shows theat different positions and different speeds.Thevalue of the red curve is the highest regardless of speed, the blue is the second,and the black is the smallest.It was found that thewas small at slow speeds, but this does not mean that the vibration reduction effect is not good for high speeds (Xieet al., 2021).Considering that the overall ground vibration in the model box and laboratory workshop increases when speed is fast, the effect was still obvious from the value of the vibration reduction, so it is determined that the new vibration isolation barrier structure can deal with the situation of high speed.

Figure 13(d) shows the damping mechanism of the new barrier.Under the action of traffic load, the damping effect mainly depends on the efficiency of the transmission wave.As the figure shows, there are many granular structures on the surface of the concrete canvas,which can have a significant effect on the direction of the horizontal transmission waves, thus greatly reducing the transmission efficiency of vibration waves.If we take an infinitesimal unit section for the new composite barrier structure, the friction between the barrier structure and subgrade soil is calculated as follows:

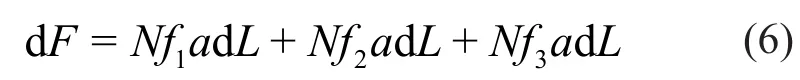
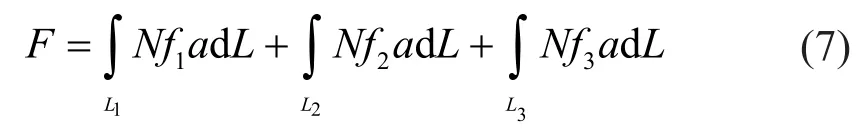
whereNis normal stress;f1andf2are the friction coefficient between the subgrade and the left and right surfaces of the concrete canvas,f3is the friction coefficient between the PE water bag and the subgrade soil,ais the width of the reinforcement material, andL1andL2the length of the left and right contact surface between the subgrade and the concrete canvas, respectively.L3is the length of the contact surface of the subgrade soil and the PE water bag.Therefore, the new barrier structure is better than the traditional barrier for both the transmission efficiency of the vibration wave and the friction response of the barrier to the surrounding subgrade soil.

4.3 Response analysis of soil stress in the subgrade

The empirical formula for the effective soil stressδin the subgrade can be expressed as:

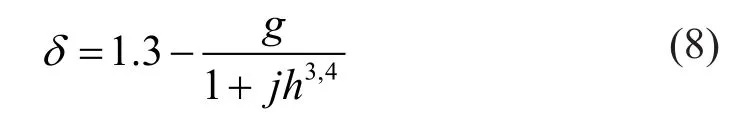
in whichgandjare two empirical parameters.

As shown in Fig.14, the measured effective soil stress data are compared with the empirical formula in the case of two different speeds.The figure shows thatthere is a certain nonlinear relationship between most of the test data and Eq.(8).At the same time, it is observed that the difference between the relative error and the empirical formula under the two speed conditions is small, and the results show strong consistency.

Fig.14 Effective soil stress at different measured points

5 Conclusions

In this study, a series of large-scale model tests were carried out for a new type of composite barrier(honeycomb concrete canvas, and PE and rubber water bags) to study its vibration reduction effect under different upper loads and moving speeds.Through experiments and result analysis, the following conclusions can be drawn.

(1) With an increase in the speed of a simulated moving load, the action time interval of the train shaft on the track is reduced, and the impact effect on the track increases, so that the vibration response of the surrounding environment increases.For the simulated moving load, when the speed is increased from 36 km/h to 180 km/h, the vibration velocity on the surface of subgrade is increased from 0.48 m/s to 2.5 m/s.

(2) A new barrier structure (hexagonal concrete canvas combined with PE polymer water bags) can reduce vibration.When the simulated train speed increases, the damping effect of the barrier is improved.At a speed of 180 km/h, the amplitude at 1.5 m after the barrier is 48.6% lower than that before the barrier.The velocity decreases by 24.2% at 36 km/h and by 38.1%at 108 km/h.

(3) The velocity amplitudes before and after the installation of the new barrier show that the new barrier has a better vibration absorption effect on the moving load with large speed.

Acknowledgment

This work was supported by the National Natural Science Foundation of China under Grant Nos.52078387 and 51578425, and the Natural Foundation Project of Zhejiang Province under Grant No.LY18E080027.