基于小波去噪的优化灰色模型在变形监测中的应用
2022-07-12范飞玲黄基峻
范飞玲 黄基峻
(1.庆元县规划测绘设计院 浙江丽水 323800;2.广西机电工业学校 广西南宁 530023)
由于受到自然或者人为因素的影响,建筑物在施工或者运营阶段不可避免地会发生变形,对其进行沉降监测意义重大[1]。建筑物沉降监测是对建筑物的沉降过程进行严格监控,观测是否会发生超临界沉降情况,以便将沉降变形控制在合理范围内,从而保证工程安全实施。
小波去噪在处理数据时能够剔除原始数据中的异常值,使原始数据序列更加平滑。灰色模型是常用的沉降预测模型,但数据预测呈指数变化形式,预测结果与实际工况存在差异,如果采用恒正凹化和相邻均值法对原始数据进行预处理能较好地弥补这一缺点,提高模型精度。本文以某建设项目建筑物形变监测为研究对象,基于小波去噪理论和灰色GM(1,1)理论,构建GM(1,1)模型和优化GM(1,1)模型,根据重构去噪前后预测模型,对预测结果和实测数据进行对比分析。
1 小波阈值法去噪
当信号中混有噪声时,小波阈值法可以很好地抑制噪声。小波阈值法去噪的前提是噪声都具有相同的幅值,因此,可以通过设置一个阈值,将幅值低于该阈值的小波系数置为0,高于该阈值的小波系数完全保留, 或者做相应的“收缩”(shrinkage)处理,达到去噪效果[2]。
变形监测数据中混有噪声信号,可表示为
s(x)=f(x)+e(i),i=1,2,…,n
(1)
式中:s(x)为变形监测数据,包含了真实变形量和确定性噪声,f(x)为真实变形量,e(i)为随机噪声。
阈值去噪中,阈值函数体现了对超过和低于阈值的小波系数的不同处理策略,是阈值去噪中关键的一步。阈值分为两类,一是硬阈值,二是软阈值。通过信号与阈值的对比,保持大于阈值的点不变,把其余的点置零,那么把它就叫作硬阈值[3]。硬阈值函数的表达式为
(2)
软阈值函数的表达式为
(3)
式中:λ为给定阈值,ω为小波系数,ωλ为赋予阈值后的小波系数,sign(*)为符号函数。
当小波系数的绝对值小于阈值时,小波系数置零,当小波系数的绝对值大于或等于阈值时,小波系数变成该点与阈值的差值,这样的阈值称为软阈值。而硬阈值则直接使用置零方法,所以软阈值的曲线较硬阈值的曲线更为光滑,效果更好。
2 灰色模型
2.1 GM(1,1)模型
GM(1,1)模型是指仅由一个变量的一阶微分方程形成的模型,其建模步骤如下:
1)累加生成。设原始序列为x(0)={x(0)(1),x(0)(2),…,x(0)(n)},对x(0)做一次累加,得到x(1)={x(1)(1),x(1)(2),…,x(1)(n)}。
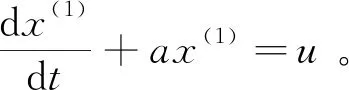
(4)

(5)

2.2 GM(1,1)模型的精度检验
为了评价GM(1,1)模型的精度,需要建立评价指标对模型的准确性进行说明。通常精度评定包括3个参数:残差大小、关联度和后验差[4]。
残差是指预测值与实测值的差值,可表示为
(6)
式中:e(k)为第k次变形监测的残差。
关联度检验是指构建的模型能否与原始数据进行较好的匹配,其匹配程度如何。


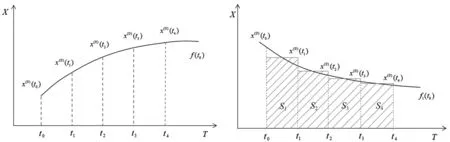
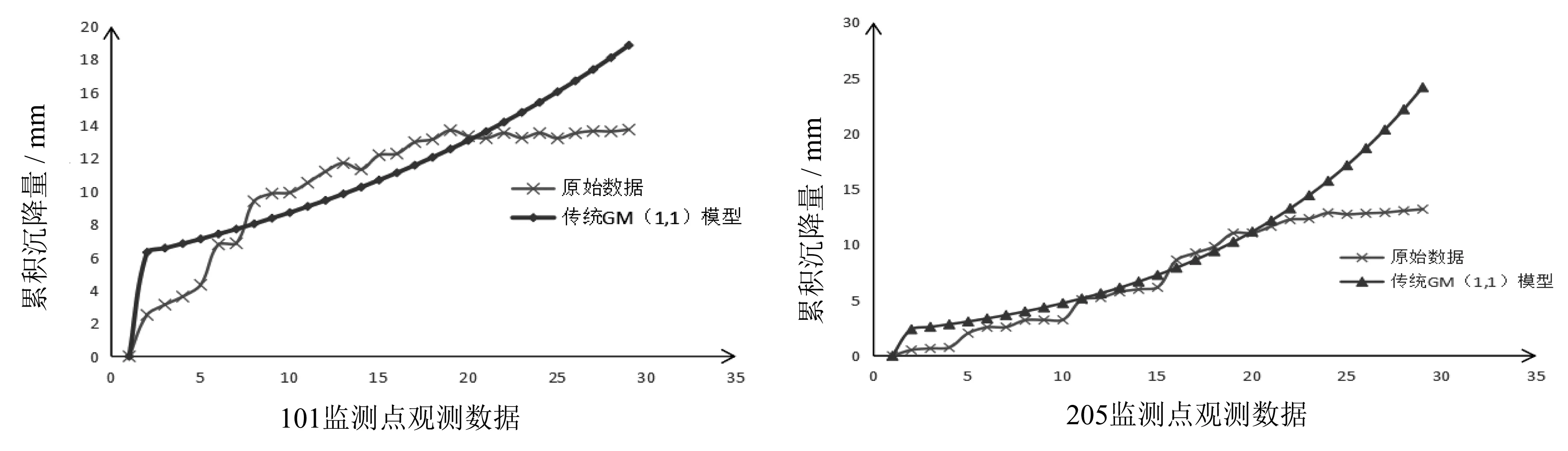
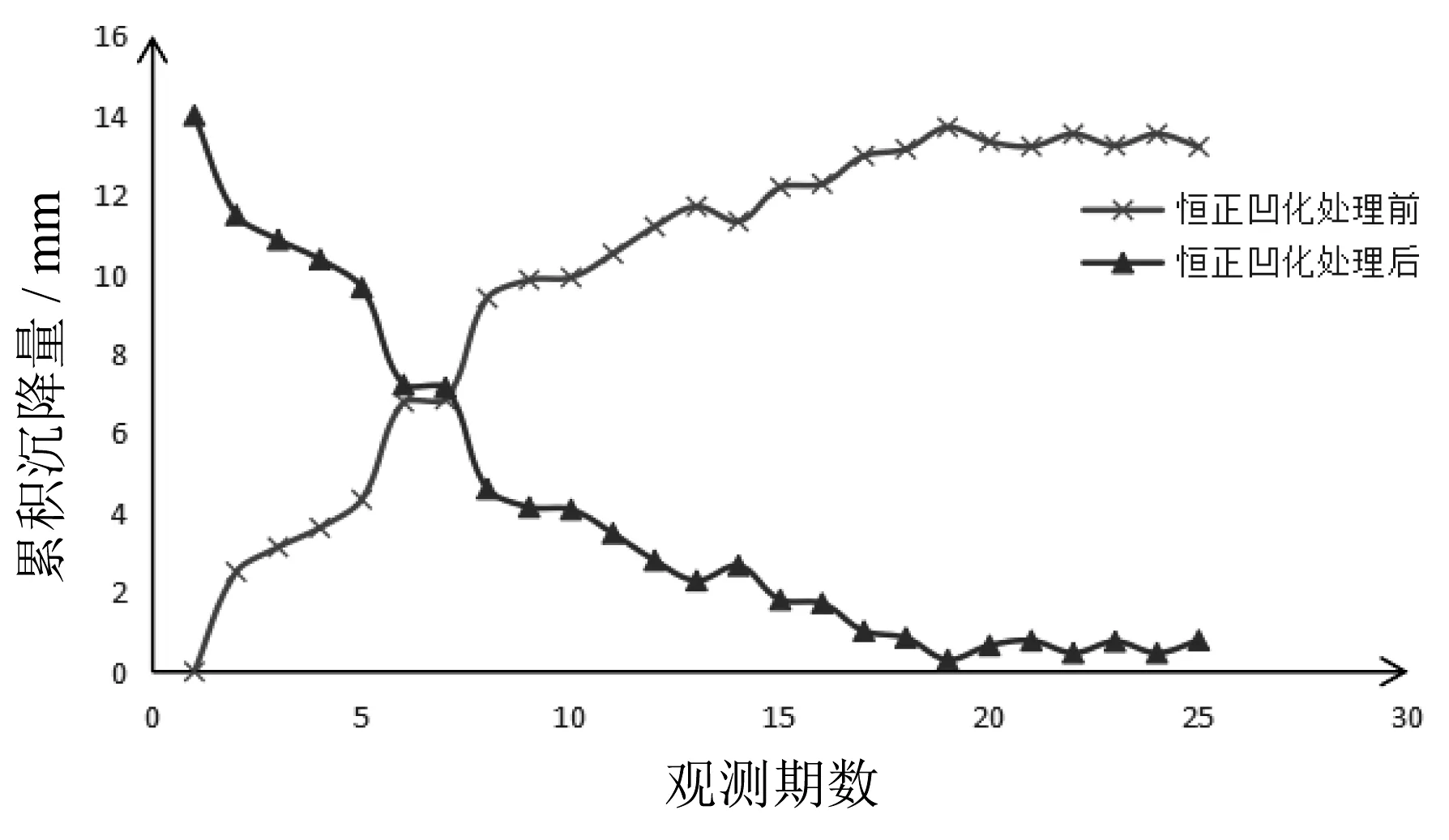
表1 模型精度等级评价Tab.1 Grade Evaluation of Model Accuracy 模型精度等级PC1级(好)0.95≤ PC ≤ 0.352级(合格)0.80≤P< 0.950.35 对于不同发展趋势的原始数据序列,其灰色GM(1,1)的建模效果不一:对于原始数据呈凹向且恒为正的序列,模型预测效果最佳;而对凸向的数据序列和非恒正的数据序列,模型预测误差较大[5]。对于这种缺陷,GM(1,1)优化模型可采用“镜像”和“平移”等手段对序列{x(0)(tk)}进行转换,使其呈现恒正凹型特性,再根据序列中相邻数据求取的平均值生成新序列{x(00)(tk-1)}。对新数列再次建模[6],同样用面积表示方程f(tx)在时区上的增量,就可以让区间前半部分通过弥补阴影部分来降低计算误差,如图1所示。 图1 GM(1,1)建模和优化GM(1,1)建模 等时距监测数据序列可表示为 {x(0)(t)}={x(0)(t1),x(0)(t2),…,x(0)(tn)} (7) 时间间距可表示为 Δti=ti-ti-1; Δtj=tj-tj-1 (8) 若Δti=Δtj,i≠j,i、j∈{1,2,…,n},则代表序列中时间间隔相等。 建模前,采用相邻均值法进行数据预处理,即对序列中所有相邻数据求取平均值生成新序列。 (9) 重新对序列{x(00)(ti)}进行建模,累加结果为 x(01)(tk)=x(00)(t1)×Δt1+x(00)(t2)× Δt2+…+x(00)(tk)×Δtk (10) 采用最小二乘法可求得发展系数a和灰作用量u,获得序列{x(00)(tk)}时间响应方程式。 (11) (12) 本文以某建设项目的一号住宅楼的101监测点和二号楼的205监测点为研究对象,项目地块以平地为主,坡度较缓,南北宽约169.84 m,东西长294.33 m。建设项目周围建筑物众多,人员密集,且分布着密集的城市地下管线,建筑变形如果超出限定范围,会导致严重的后果,所以有必要进行严格的变形监测。本次均使用这两点的29期观测数据对预测结果和实测数据进行对比分析。 在小波去噪过程中,选择的小波基函数、阈值和分解层次等因子不同,得到的去噪结果也不同[8],因此,要找到对某个监测点最优小波去噪结果,需要对不同因子不断进行对比分析。 根据小波去噪理论,一般情况下,利用软阈值进行信号处理可以获得更佳的光滑信号曲线和更理想的去噪数据[9],因此本文选择软阈值去噪法。 经过多次试验对比分析,小波去噪最终确定采用db8作为小波基函数,分解层数为1,采用无偏风险估计阈值(rigrsure)原则,设置scal=sln时,101监测点和205监测点去噪后预测成果与原始数据如图2所示。 图2 101监测点和205监测点小波去噪前后的结果 3.2.1 优化前后灰色GM(1,1)模型比较 建设项目开始阶段,101监测点和205监测点沉降速度较快,到监测后期建筑物沉降逐渐趋于稳定,总体呈“先快后慢”的趋势。采用传统GM(1,1)模型对101监测点和205监测点的前25期原始数据进行建模,再利用模型对第26期~第29期的累积沉降量进行预测。 图3 101监测点和205监测点传统GM(1,1)模型预测结果 从图3可以看出,101监测点和205监测点的原始数据与传统GM(1,1)模型预测曲线的发展趋势不一致,原始序列后期均呈现稳定趋势,而预测曲线仍在快速上升。从表2可知, 101监测点预测结果平均绝对百分比误差为30.19%,P为0.959 7,C为0.455 5,模型精度只达到2级(合格)。205监测点预测结果平均绝对百分比误差为64.16%,P为0.801 7,C为0.270 5,模型精度也达到2级(合格)。这说明传统GM(1,1)模型的拟合和预测结果相比于原始数据误差较大。 采用优化GM(1,1)模型对101监测点和205监测点进行建模。两监测点原始数据虽然都呈先快后慢趋势,但101监测点整体呈凸型,适合用优化GM(1,1)模型进行建模。 图4 101点原始数据恒正凹化处理前后对比 对于205监测点,原始数据呈先凹后凸型趋势,对于凹凸性不固定的数据,需要分段选取数据进行建模以提高预测精度。选取205监测点第15期~第25期呈凸型数据进行建模,建模过程与101监测点相同。101监测点和205监测点优化GM(1,1)模型预测结果如图5所示,精度检验情况如表2所示。 表2 传统GM(1,1)模型与优化GM(1,1)模型拟合和预测结果对比Tab.2 Comparison of Fitting and Prediction Results between Traditional GM(1,1)Model and Optimized GM(1,1) Model项 目传统GM(1,1)模型监测点101监测点205优化GM(1,1)模型监测点101监测点205数据拟合阶段数据预测阶段最大残差/mm3.794.42-1.43-0.34最大相对误差/%151.00359.62-56.187.11相对误差均值/%25.5152.887.642.32最大残差/mm5.1110.970.110.37最大相对误差/%37.1983.170.812.58平均绝对百分比误差/%30.1964.160.461.38P0.959 70.801 70.977 20.953 2C0.455 50.270 50.108 10.107 1 图5 101监测点和205监测点优化GM(1,1)模型预测结果 从图5可以看出,101监测点和205监测点的原始数据与优化GM(1,1)模型预测曲线有较好的拟合。从表2可知,101监测点优化GM(1,1)模型预测结果平均绝对误差为0.46%,P为0.977 2,C为 0.108 1,模型精度达到1级(好);205监测点预测结果平均绝对误差为1.38%,P为0.953 2,C为0.107 1,模型精度也达到1级(好)。说明优化GM(1,1)模型精度高于传统GM(1,1)模型,预测效果都有较大提升。 3.2.2 小波去噪前后优化GM(1,1)模型比较 为验证原始数据经小波去噪后能否提高建模精度,本文对使用小波去噪后的原始数据进行建模与使用原始数据进行建模的精度进行对比分析。小波去噪并没有改变原始数据的变化趋势,101点小波去噪后数据依然呈凸型,205点小波去噪后数据也依然是“先凹后凸”型。 对101监测点和205监测点采用相同方式进行优化GM(1,1)模型建模,建模过程如上。经小波去噪后的101监测点和205监测点优化GM(1,1)模型的处理结果如表3所示。 从表3可以看出,由于101监测点和205监测点数据在监测后期数据变化较为平稳,导致小波去噪效果不明显,因此小波去噪前后预测值没有较大改变。对于101监测点,小波去噪前后的优化GM(1,1)模型预测数据没有变化;对于205监测点,去噪后优化GM(1,1)模型的均方误差、平方和误差和平均绝对百分比误差相对于小波去噪前优化GM(1,1)模型,精度有较大提高。 表3 小波去噪前后101监测点和205监测点优化GM(1,1)模型精度对比Tab.3 Accuracy Comparison of Optimized GM(1,1)Model between 101 Monitoring Point and 205 Monitoring Point before and after Wavelet Denoising项 目小波去噪前监测点101监测点205小波去噪后监测点101监测点205误差均值/%7.642.326.982.51平均绝对百分比误差/%0.461.380.460.54均方误差/mm0.036 70.105 90.036 70.085 7平方和误差/mm0.021 50.179 30.021 50.121 7 本文针对传统GM(1,1)模型在沉降变形预测上的不足,优化GM(1,1)模型。利用恒正凹法对原始数据数列进行了数据预处理,并采用了相邻均值法重新构建了一阶累加序列,让坐标系中函数在同一时段的点前后面积能够差值互补,从而能更准确地描述原始序列的真实变化,进而降低GM(1,1)模型拟合误差,而且优化GM(1,1)模型的精度高于传统GM(1,1)模型,预测效果有较大提升。 在优化GM(1,1)的基础上,提出小波去噪数据处理方式,去噪后的优化GM(1,1)预测模型能较好地对沉降趋势进行预测,模型精度更高,预测结果更为可靠,其结果对工程安全施工具有一定的指导意义。2.3 优化GM(1,1)模型
3 工程实例验证
3.1 监测数据小波去噪

3.2 灰色GM(1,1)模型比较
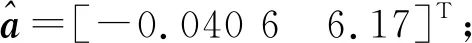




4 结 语
