一种融合形态学与渐进三角网的滤波算法
2022-07-12张启光
张启光
(烟台市福山区自然资源局 山东烟台 265500)
得益于近年来软硬设备的不断完善,机载LiDAR得到了长足的发展,已成为快速获取地表信息的重要工具[1-2]。点云滤波作为将地物点与地面点分离的算法,在点云数据处理阶段工作量庞大。因此,对高精度点云滤波的研究,依然是当前研究的重点内容[3]。
常用的点云滤波算法分为渐进三角网滤波算法、基于形态学的滤波算法、基于坡度的滤波算法和基于曲面拟合的滤波算法等。其中,渐进三角网滤波算法因其具有较好的滤波性能而被广泛关注并加以改进。例如,隋立春等[4]提出基于渐进三角网的机载LiDAR点云数据滤波算法,对点云网格进行划分,对网格内点云按照高程由小到大排序,每次选取网格内最低点进行判断。试验结果表明,该算法能有效地滤除不同尺寸的建筑物、低矮植被和其他地物,地形特征保持较好。 杨娜[5]提出一种光滑表面分割的渐进三角网加密滤波算法,将光滑表面分割融入到地面点选取的过程中,以获取更多的种子点,有效地提高了点云分割结果的准确性。LINDENBERGER J[6]将形态学算法运用到点云滤波处理中,对某一固定窗口内点云开运算,以运算前后高差为依据来确定点云归属。为提高滤波精度,ZHANG K Q等[7]对形态学滤波加以改进,通过逐渐改变窗口尺寸并设置适合窗口尺寸的高差阈值,取得了更好的滤波结果。基于坡度的滤波方法被提出后,SITHOLE G[8]在基于坡度的滤波方法基础上,充分考虑地形起伏的影响,通过设计坡度核函数使得滤波阈值随着地形坡度动态变化。基于曲面拟合的滤波算法本质上是通过点到表面模型的残差等特征来实现点云类属的判断,张小红等[9]首次将“移动曲面拟合预测”滤波算法用于机载激光扫描测高数据滤波处理,将地面假设为复杂空间曲面,在局部区域用简单的二次曲面进行逼近,若脚点到二次曲面的距离过大,则作为地物点滤除。试验结果表明,该算法自适应性强,计算速度快,滤波效果好。
目前,点云滤波的研究更多的是致力于点云过滤流程的分步式处理。王云云等[10]提出一种植被茂密地区的点云自适应双重滤波方法,利用回波分离等方法实现了点云过滤由粗到精的处理。试验结果表明,结合回波信息和高差信息的双重滤波方法不仅能较好地剔除植被,而且能较好地保留地形细节。国际摄影测量协会(ISPRS)第三工作小组主要研究航空影像、LiDAR点云等数据在复杂场景下的地物检测与建模。ISPRS第三工作小组曾选取渐进三角网滤波算法和形态学滤波算法等8种经典滤波算法进行试验测试,结果发现各滤波器在低复杂度的环境中表现良好,但在地物复杂或地形起伏较大的场景下,均表现平平[11-14]。针对单一滤波均存在可靠性差、无法适用于各种地形等问题,本文提出一种形态学与渐进三角网融合的滤波算法,探究融合滤波在不同场景下的滤波性能。
1 单一滤波方法概述
渐进三角网滤波首先将点云格网化,选取格网最低点构成三角网,依据判断点到三角网的距离(d)与点到三角网顶点的角度(α、β、γ)来判断点属类别,然后将地面点加入构网,可逐渐加密初始三角网,直至得到精确的地面模型,其原理如图1所示。作为精度较高的一种滤波算法,渐进三角网滤波在复杂区域的滤波效果却不尽如人意,主要是因为地面种子点的选取个数有限,组成的三角网由于稀疏而无法准确表达真实地面,且在地形起伏较大的区域,局部地形对阈值影响较大,采用固定阈值或全局阈值均无法顾及不同地形[14]。因此渐进三角网滤波在全地形的适应性依然较差。
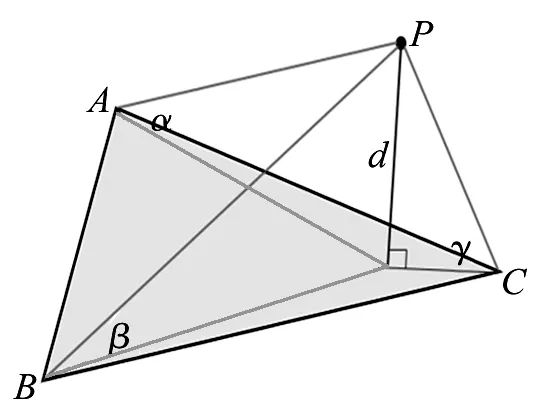
图1 TIN模型判断示意图
形态学滤波主要依靠开运算实现点云类属判断。开运算是对某一区域先腐蚀(即取区域内点云的最低点),再膨胀(即取区域内点云的最高点)。移动某一特定窗口扫描整个点云区域,将运算前后高差过大的点判定为地物点,即可得到地物点与地面点两种点云类型,如图2所示。其中,dhp为p点的两次滤波高差,dhT为高差阈值,当高差小于此阈值时,可将p点归类为地物点。形态学滤波算法简单、效率较高,可广泛用于大区域的点云滤波,但精度较低,若要实现较为优异的滤波效果,人工处理工作量较大。
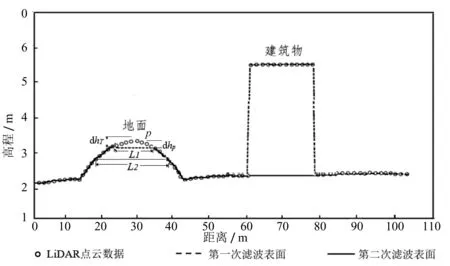
图2 渐进形态学滤波示意图
2 形态学与渐进三角网融合滤波算法及其试验结果分析
受限于单一滤波的局限性,复杂度较高区域的滤波结果依然无法满足高精度数据处理的要求。为进一步提高滤波的可靠性与准确性,将成熟滤波算法融合,得到性能更优异的算法成为一种可行的研究方向。形态学滤波精度较低,但适合大场景下的快速处理,而渐进三角网滤波精度稍高,但受地面种子点选取与局部地形影响明显,故两种滤波算法存在互补性。本文将探讨形态学与渐进三角网两种算法的融合。
2.1 基于形态学的地面种子点选取
利用形态学滤波快速得到大量的地面点,将这些点作为渐进三角网滤波的初始地面点,构成稠密的地面三角网,与由数点组成的稀疏三角网相比,该三角网模型可更准确地表达真实地面。选取的地面种子点由辅助点、格网最低点、可靠地面点构成,其中,辅助点和格网最低点通过传统渐进三角网滤波算法选取的地面种子点,极为稀疏,可靠地面点通过形态学滤波得到。因此,将可靠地面点加入构网,可极大地增加三角网与真实地面的贴近程度,如图3所示。

图3 初始地面种子点选取的改进
2.2 顾及地形的改进滤波阈值
充分考虑局部地形对角度阈值参数的影响,利用统计形态学,计算地面三角网的法向量竖直角作为全局角度阈值,计算判断点所在三角网法向量竖直角,作为该判断点角度阈值修正值。角度阈值可表示为
(1)

充分考虑局部地形对距离阈值参数的影响,计算判断点所在三角网两点间的高差及坡度角,作为该判断点距离阈值修正值。距离阈值可表示为
(2)
式中:thd为距离阈值;hg为距离阈值设置的较小固定值,可在0.1~0.3中取值;C为形态学滤波得到的地面点云平均间隔;L为三角网最大边长,当三角网较小(L<3C)时,将距离阈值thd设置为较小的固定值hg;hmax为最大阈值,要防止阈值设置过大,纳入错误地面点。
距离阈值的改进示意图如图4所示,图中Δhi、αi分别为三角网两点间高差及坡度角。

图4 距离阈值的改进示意图
2.3 试验结果与分析
2.3.1 评价指标
为测定各种滤波算法的可行性,ISPRS第三工作小组提供的一份标准数据集中包含了城区数据及乡村数据,从中选取了15份样本数据,通过人工进行精确分类,用于点云滤波算法结果分析。为了定量描述滤波误差,ISPRS第三工作小组制定了统一的评价标准,共定义了3种误差,如表1所示。
2.3.2 定性评价与分析
本试验通过分析滤波结果生成的DEM是否可靠来对滤波算法进行定性评价。鉴于渐进三角网滤波算法是公认的较为优异的滤波算法,本文通过基于形态学与渐进三角网融合滤波算法(简称融合滤波算法)的结果与传统渐进三角网滤波算法的结果进行对比(见图5),评价融合滤波算法的优越性。

表1 滤波误差定义Tab.1 Definitions of Filtering Error类 别滤波地面点/个滤波地物点/个总数/个误差/%参考地面点abe=a+bb/e (第Ⅰ类误差)参考地物点cdf=c+dc/f (第Ⅱ类误差)总 数n=e+f(b+c)/n (总误差)

图5 滤波结果
滤波结果图中,浅灰代表地物点,深灰代表地面点。由图5可知,在地形较为陡峭的方框区域,传统算法将部分地面点误判为地物点,而融合滤波算法保留了此处的地面点;在黑圈区域,传统渐进三角网滤波丢失了部分建筑物,而融合滤波算法归类正确。从两种算法得到地面点生成的DEM可以看到,所生成的DEM均能表达地面模型,但融合滤波算法在局部区域的表达效果明显更优,传统算法要么过度平滑,如黑圈区域DEM地形被过度平滑,要么出现了毛刺,如方框区域DEM中建筑物未能有效去除,产生毛刺。
2.3.3 定量评价与分析
为进一步评价融合滤波算法的性能,采用ISRRS 第三工作小组定义的3类误差作为评价标准,探究融合滤波算法在不同场景下的效果,结果如表2所示。其中,CG和CN表示参考地面点与参考地物点个数,LG和LN表示滤波地面点与滤波地物点个数,E为各类误差。

表2 融合滤波算法结果统计Tab.2 Result Statistics of Fusion Filtering Algorithm样本类别LGLNE/%samp11samp31samp51CG18 9882 74612.63CN1 35814 7768.42CG14 9316284.04CN13412 8521.03CG13 7891240.89CN1243 7713.1810.842.701.39样本类别LGLNE/%samp21samp41samp61CG9 8771991.18CN3462 32312.90CG5 54875011.91CN2565 2434.65CG33 4324251.25CN321 1712.674.278.531.37
从表2可以看出,滤波误差整体处于较低水平,除samp11与samp41的第Ⅰ类误差、samp21的第Ⅱ类误差、samp11总误差大于10%外,其余误差均小于10%。说明融合滤波算法在不同场景下的滤波效能良好,在地物类型各异、地形起伏复杂的各区域中,均能取得较好的结果。
为进一步探究融合滤波算法的可行性与稳定性,与ISPRS第三工作小组测试的8种滤波算法进行对比,各种算法的误差统计结果如图6所示。其中,We为融合滤波算法误差结果。

图6 融合滤波算法与8种经典滤波结果精度统计
由图6可知,融合滤波算法在第Ⅰ类误差和总误差方面较为优越,误差稳定在10%及以下,基本处于各算法的最优水平,具有较强的可靠性与适应性,但在第Ⅱ类误差上分布较为离散。由于第Ⅱ类误差主要是由误分地面点引起的,这部分点通常高悬于真实地面点上方,较易剔除,因此,取得较小的第Ⅰ类误差与总误差更为重要[14]。
在ISPRS第三工作小组的滤波测试中,渐进三角网滤波整体表现较好,而本文提出的融合滤波算法将形态学滤波算法融入渐进三角网滤波中,本质上解决了渐进三角网滤波的种子点选取及局部地形不稳定性等问题,因此,在与8种滤波方法的对比中效果最好。
3 结 语
为了解决单一滤波在复杂区域的不稳定性问题,本文研究了一种融合形态学滤波与渐进三角网滤波的滤波算法。针对初始地面模型较为粗糙的问题,利用形态学滤波为渐进三角网滤波提供大量的可靠地面种子点,为后续点云类属判断提供更为精确的地面模型;针对判断阈值无法适应全地形的问题,利用渐进三角网滤波法的法向量竖直角、两点间高差及坡度修正角度阈值和距离阈值,充分考虑了局部地形对阈值参数的影响。
试验结果表明,相较于单一滤波,基于形态学滤波与渐进三角网融合滤波算法效果明显更优,即使在地形陡峭的区域中也可取得较好的滤波效果,本文提出的方法具有较高的可靠性与适应性。同时,本文通过与ISPRS第三工作小组测试的8种经典的滤波方法进行对比,证明了基于形态学滤波与渐进三角网融合滤波算法在第Ⅰ类误差和总误差方面的优势明显。
