取药机器人机械结构设计及有限元分析

刘邦彦，张凤生，程堂灿

(青岛大学，山东 青岛 266071)

0 引言

随着自动化、信息化和人工智能等技术的发展，药房自动化已成为医疗事业发展的必然趋势，尤其是“智慧药房”的提出使得药房自动化设备的发展面临新的机遇和挑战[1]。目前，国内大中型医院应用较为广泛的为机械手式自动发药设备和储药槽式自动发药设备[2]。前者每次可出药品数量较少，难以满足庞大就医人群的需要，后者因出药量大，更适应国内的医疗现状，但设备成本高，且灵活性不如前者。为了提高机械手式自动化药房取药效率，本文对本课题组前期设计的取药机器人样机进行改进，通过对机械结构的动力学特性及主要承载件进行有限元分析，在确保机械结构强度与刚度的前提下，优化结构设计，使其轻量化，同时应用视觉检测定位降低成本。

1 取药机器人总体方案设计

利用机器人代替人穿梭于药架之间抓取药品是典型的自动化药房型式之一，其药品储量容易扩展，对药品包装型式、外观形状、尺寸适应性好，总体成本较低。

根据取药机器人运动范围大、速度快、负载小等特点，采用具有行程长、精度高、速度快、易于扩展和维护的直角坐标型机器人[3]，其总体方案设计如图1所示。X轴：机器人沿两排药架之间水平运动；Z轴：沿药架高度方向竖直升降运动；Y轴：末端执行器的夹指沿垂直于药架方向伸缩运动；Q轴：夹指夹取/松开药盒的动作；R轴：末端执行器可左、右回转，使一个机器人能够兼顾从左、右两侧的药架取药。

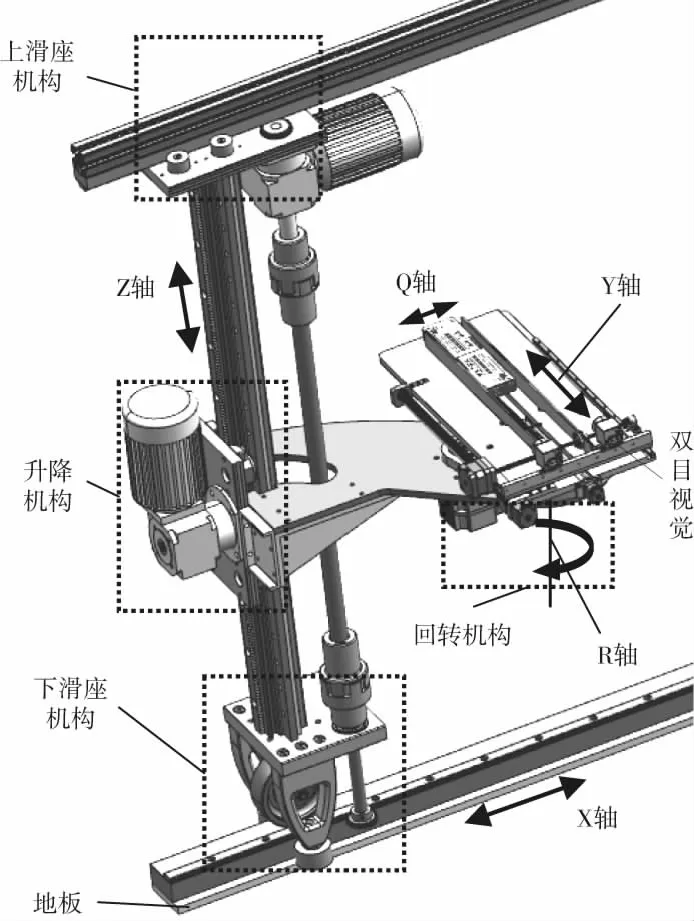
图1 取药机器人3D设计模型

机器人取药过程：药房管理系统的主控计算机将取药信息传给控制机器人的下位机。对于自动化药房系统，每种药品在药架上的位置信息均存在于管理系统中，因此机器人在下位机控制下沿X轴和/或Z轴快速运动到目标药品所在位置。然后，末端执行器绕R轴旋转指向目标药盒，并通过视觉双目视觉检测药盒位置，再由夹指夹取(沿Y轴、Q轴动作)药盒。

由于取药机器人运动跨度大、速度快，若仅依靠机械运动机构来实现高精度的运动与定位，以保证对目标药盒的准确抓取，则对机器人机械系统的制造精度、运行可靠性与稳定性要求就非常高，导致成本大幅增加。为此，在末端执行器上加装双目视觉系统[4]。先由机械系统实现机器人快速运动，到达目标药盒所在位置，实现粗定位；再由视觉系统检测药盒位置，实现准确定位从而降低对机械系统与控制系统的要求。

2 取药机器人机械结构设计

2.1 运动机构设计

取药机器人运动机构主要包括上滑座、下滑座、升降机构和回转机构四部分，如图2(本文不包含末端执行器)。电机驱动一根贯通上下的驱动轴，通过上、下滑座处的齿轮齿条啮合，带动上、下滑座沿X轴同步移动。上滑座由四个平滚轮轴承保证沿导轨方向平行移动，下滑座由滚轮承重，并用两个平滚轮轴承保证沿导轨方向平行移动；升降机构与滑座机构类似，由“电机+减速器+齿轮齿条传动”驱动升降机构；升降机构通过弧形承载板与回转机构相连，末端执行器则安装于回转机构上。为使结构受力更合理，升降机构的电机与减速器和回转机构“对称”分布在竖直导轨的两侧来平衡配重；回转机构由电机带动同步轮，通过同步齿形带与V型滚轮圆弧齿条导轨(简称圆弧导轨)的外齿圈啮合，并在V型滚轮轴承的支撑下使圆弧导轨做回转运动，进而通过法兰带动末端执行器旋转。

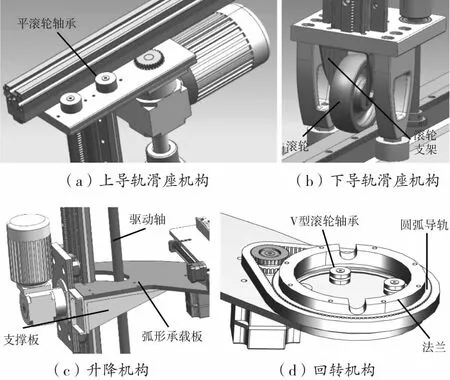
图2 取药机器人机械结构局部示意图

2.2 机器人运动机构力学分析与计算

根据设计要求，机器人主要技术参数：X轴行程0～4510 mm，最大速度1.4 m/s；Z轴行程0～2490 mm，最大速度1.4 m/s；R轴回转运动范围0～180°，最大速度75°/s。

(1)回转机构

回转机构电机的选型与计算[5]：回转机构简图见图3。设计参数：同步轮质量m1=0.22 kg，直径DPM=46.53 mm，齿数z1=30，转动惯量为JPM=0.5m1(DPM/2)2=5.954×10-5kg·m2；圆弧导轨齿数z2=120，故同步带传动比Nr=z2/z1=4，传动效率η=0.98。圆弧导轨、法兰及末端执行器的总质量约为m2=12 kg，末端整体结构重心与回转中心轴线的距离为r=0 mm，圆弧导轨直径DPL=189.8 mm，其整体转动惯量为：

JPL=0.5m2(DPL/2)2+m2r2=0.054 kg·m2

等效到电机轴上的转动惯量为：

JPL→M=(1/Nr)2JPL=3.375×103kg·m2

同步齿形带质量为：m3≈0.146 kg，等效到电机轴上的转动惯量为：

则电机轴上的总转动惯量为：

JL=JPM+JPL→M+JB→M=51.5×10-4kg·m2

根据设计要求，回转运动速度为70°/s，回转过程中加速运动时间为t1=0.15 s，匀速运动时间为t2=0.9 s，减速运动时间为t3=0.15 s。

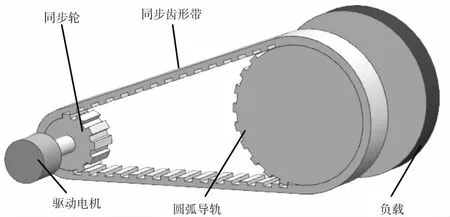
图3 回转机构的同步带传动简图

经计算，初选松下MGMF 850 W低速大转矩中惯量伺服电机[6]，电机与同步轮直连，不使用减速器，主要技术参数：额定功率850 W，额定转矩5.41 N·m，瞬时最大转矩14.3 N·m，额定转速3000 rpm，最高转子惯量JM=7.4×10-4kg·m2。

选型合理性分析：惯量比为JL/JM≈6.96，小于电机的推荐负载惯量比10；由圆弧导轨的回转速度75°/s，可知其转速为n2=5/24 (r/s)，同步带传动比Nr=4，则同步轮转速为n1=n2Nr=50 rpm，由于电机与同步轮之间不使用减速器，等效到电机轴上的转速即为同步轮的转速，远小于电机的额定转速；转矩：圆弧导轨运动时，主要克服与V型滚轮轴承之间的摩擦力。设摩擦系数μ=0.1，则匀速运行时等效到电机轴上的转矩为：

Tf=μm2gDPM/2ηNr=0.285 N·m

加速时为：

Ta=Tf+(JL+JM)×2πn1/60t1=0.490 N·m

减速时为：

Td=Tf-(JL+JM)×2πn1/60t1=0.079 N·m

加速时的瞬时最大转矩：

Ta=0.490 N·m<14.3 N·m

有效转矩为：

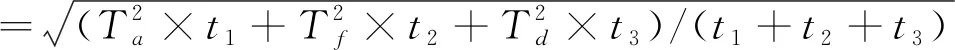
=0.3174 N·m<5.41 N·m。

以上分析计算表明，所选电机满足设计要求。

(2)升降机构

升降机构驱动电机的选型与计算：升降机构中轴型小齿轮的质量mG=0.369 kg，直径DG=45 mm，转动惯量JG=0.5mG(DG/2)2=9.34×10-5kg·m2；减速器传动比i=5，转动惯量Jg=1.0×10-4kg·m2。根据UG建模设计的零部件参数及材料，计算升降运动部分总质量约为M=26 kg。

机器人升降运动过程如图3所示。启动加速运动时间t1，匀速运动时间为t2，减速运动时间t3，取药时间t4是机器人运动到目标药盒高度时至取完药后开始返程时的间隔。设计采用的HEPCO直线导轨系统运行速度最高为10 m/s，加速度最高2g(g=9.8 m/s2)，满足本文最大运行速度Vmax=1.4 m/s、加速度a=Vmax/t1=3.5 m/s2的要求。

图4 升降运动过程

升降机构由电机通过减速器驱动齿轮，齿轮与齿条啮合，沿着齿条做竖直升降运动。减速器传动比i=5，等效到电机轴上的总负载惯量JL为齿轮等效到电机轴上的转动惯量与减速器的转动惯量之和，即JL=JG/i2+Jg=1.04×10-4kg·m2。

根据以上分析计算，初选松下MSMF 750 W低惯量带刹车功能的伺服电机，其主要技术参数：额定功率750 W，额定转矩2.39 N·m，瞬时最大转矩7.16 N·m，额定转速3000 rpm，最高转速转子惯量1.06×10-4kg·m2。对于最大运行速度Vmax=1.4 m/s，等效到电机轴上的转速为2970.9 rpm<额定转速3000 rpm；实际瞬时最大转矩1.931 N·m<7.16 N·m，实际有效转矩1.104 N·m小于电机额定转矩2.39 N·m。实际惯量比为(1.04×10-4)/(1.06×10-4)=0.98倍，远小于电机推荐的负载惯量比20倍。因此，所选电机满足设计要求

(3)水平运动机构

水平运动机构驱动电机的选型与计算：与升降机构驱动电机的选型计算过程类似，水平运动机构也选取松下MSMF 400 W伺服电机，主要技术参数：额定功率400 W，额定转距1.27 N·m，瞬时最大转矩3.82 N·m，额定转速3000 rpm，最高转速转子惯量0.3×10-4kg·m2。配备减速比i=5减速器。

经分析计算，水平运动的总质量约为m总=98.92 kg，等效到电机轴上的负载惯量为2.02×1-4kg·m2，最大运行速度Vmax=1.4 m/s对应的电机转速为2970.9 rpm<额定转速3000 rpm；加速时的瞬时最大转矩为0.622 N·m，小于电机额定转矩1.27 N·m；有效转矩为0.197 N·m，小于电机额定转矩1.27 N·m；实际惯量比为(2.02×10-4)/(0.30×10-4)=6.73倍，远小于电机的推荐负载惯量比30倍。因此，所选电机满足设计要求。

3 关键零部件的有限元分析[7]

3.1 下承载滑座有限元分析

下承载滑座承受机器人所有移动零部件的重量，需通过有限元分析，验证其强度和刚度是否满足要求。将下滑座的UG三维模型导入ANSYS Workbench生成有限元模型，滑座材料为铝合金，密度2770 kg/m3，弹性模量7.1×104MPa，屈服强度280 MPa，泊松比0.33，取安全系数ns=2，则许用应力为[σ]=σs/ns=140 MPa，其中σs为屈服强度。

采用自动网格划分，并对各圆孔处的网格进行细化处理。下滑座承受的总负载为f总=m4g=969.42 N，并在滚轮的安装轴承处固定约束，仿真结果如图5所示。

图5(a)中，最大变形为0.0224 mm，发生在下承载滑座的边缘，该变形量对机器人的定位精度影响微小。图5(b)中最大应力为37.524 MPa，发生在滚轮轴承的安装孔处，其值远小于承载下滑座的许用应力140 MPa，表明承载滑座满足刚度和强度的要求。

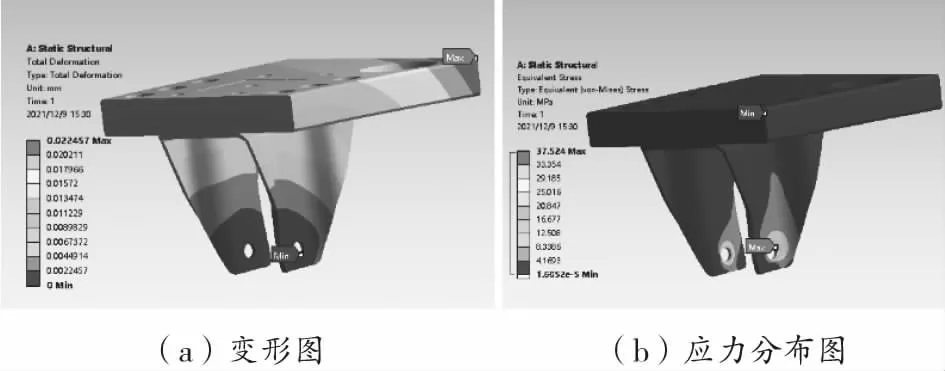
图5 下滑座有限元分析

3.2 驱动轴有限元分析

驱动轴长径比大，且承受扭矩较大。将驱动轴的UG三维模型导入ANSYS Workbench中生成有限元模型，材料为结构钢，密度7850 kg/m3，弹性模量2×105MPa，屈服强度250 MPa，泊松比0.3，安全系数取2，则许用应力为125 MPa。

根据上文计算，驱动轴受到最大力矩为1.310 N·m，对下端安装联轴器处施加固定约束。采用自动网格划分，仿真结果为最大变形为0.0247 mm、最大应力为3.9358 MPa，发生在上端与连轴器连接处，其数值很小，满足刚度和强度的要求。

3.3 弧形承载板有限元分析

弧形承载板将回转机构与升降机构相连，承载板为悬臂结构，其承受的载荷为回转机构和末端执行器的总重量及升降机构加速运动时的附加载荷。

为减轻重量，便于机器人快捷运动，弧形承载板及两个支撑板均采用铝合金(与下承载滑座材料相同)。将弧形承载板及支撑板的UG三维模型导入ANSYS Workbench中生成有限元模型，并进行自动网格划分；对承载板上的4个电机安装孔和5个V型滚轮轴承安装孔处进行细化处理，划分得到169889个节点和102550个单元。

负载和约束的施加：回转电机施加最大负载41.44 N，均匀分布在电机的4个安装孔处；圆弧导轨及其上的最大负载合计为132 N，均匀分布在V型滚轮轴承的5个安装孔处；承载板整体施加自重载荷和加速运动时的附加载荷；对两个支撑板与升降机构连接的面施加固定约束，如图6所示。图7为初始设计承载板厚度t=8 mm、支撑板长度L=175 mm得到的有限元分析结果。

图6 承载板网格划分与载荷施加图

由图7(a)可知，弧形承载板最大变形为2.908 mm，发生在弧形承载板的悬臂边缘处，变形量过大，不满足刚度要求。图7(b)中，最大应力为53.146 MPa，发生在弧形承载板与内侧连接件接触处，其值远小于承载板的许用应力125 MPa，满足强度要求。

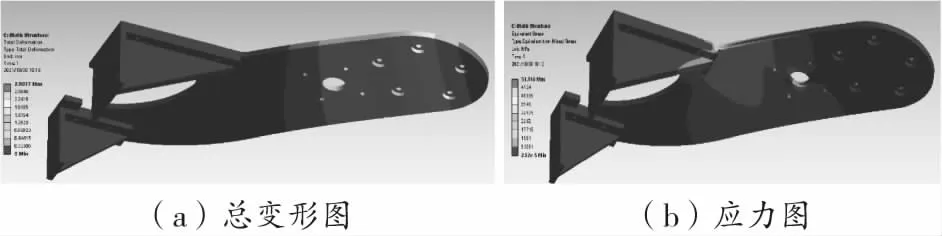
图7 承载板分析云图

针对弧形承载板边缘处变形量过大的问题，对弧形承载板和支撑板参数进行优化。采用控制变量法进行对比分析[8]，以确定t和L的优选方案。①L=175 mm，t=10 mm；②L=175 mm，t=12 mm；③t=8 mm，L=215 mm；④t=8 mm，L=255 mm。

对4种方案进行有限元分析，分别得到弧形承载板的变形与应力分布情况，结果表明：①～④的最大应力都远小于材料的许用应力；最大变形量与原设计相比，①减小40.68%；②减小63.37%；③减少28.95%；④减少50.22%。可见，随t的增加，最大变形量减少幅度明显，但增加板厚会明显增大升降机构的负载。

综合上述分析，最终确定承载板厚度10 mm，支撑板长255 mm，其最大应力19.348 MPa，远小于许用应力，最大变形量0.838 mm，比初始方案中的2.908 mm减少71.18%。

图8 最终方案弧形承载板改进方案分析云图

4 总结

直角坐标机器人具有大行程和高动态特性的特点，更适用于取药机器人应用；文中设计的取药机器人系统大部分零部件为标准件，有助于降低成本；通过在末端执行器上加装视觉系统，实现对目标药盒的检测定位，可降低对机械系统与控制系统的运动定位精度的要求。对机器人系统中关键件进行受力分析与有限元仿真，为关键件的材料选择、结构形式与参数优化提供了依据；在满足系统强度、刚度要求的前提下，使得结构紧凑、质量减轻。