非规则激励下浅水液舱晃荡数值模拟
2022-07-11石留斌李廷秋
石留斌 李廷秋 苏 焱
(武汉理工大学船海与能源动力工程学院 武汉 430063)
0 引 言
随着液化石油气(LPG)船舶,液化天然气(LNG)船舶及超大型液化天然气(VLGC)船舶的需求不断增加,船舶液舱晃荡现象逐渐成为研究热点.
Faltinsen[1]采用解析、数值,以及实验方法对液舱晃荡运动问题进行了系统研究.Ebrahimian等[2]采用边界元方法确定带有挡板的轴对称容器中对称和非对称晃荡固有频率和振型.Cho等[3]运用有限元方法(FEM),计算分析了在不同充液率和激励振幅时二维液舱晃荡运动,并将数值计算结果与线性理论计算结果进行了比较.Wu等[4]基于二维Navier-Stokes方程运用有限差分法(FDM),研究在纵荡和横荡耦合激励条件下,内部挡板结构对晃荡运动的影响并通过实验验证数值结果的可靠性.卫志军等[5]采用光滑粒子水动力学法(SPH)对二维矩形液舱晃荡运动进行研究,结果表明:SPH方法可以很好地模拟液体晃荡时水跃、破碎等自由液面的大变形运动.陈翔等[6]将移动粒子半隐式法(MPS)与图形处理器(GPU)并行加速技术相结合,对LNG船舶液舱晃荡进行了数值模拟,并将LNG船舶液舱与方型液舱的晃荡运动进行对比.结果表明:在高充液率下LNG型液舱可以有效地减小晃荡运动幅值和壁面砰击压力,但在中低充液率下,LNG型液舱则会加剧晃荡运动.王庆丰等[7]采用去奇异边界元方法,在时域内建立液舱内不规则晃荡运动数值模型,模拟了规则激励下液舱晃荡运动并与解析解进行对比验证其准确性,在此基础上完成了非规则激励下液舱晃荡运动的数值模拟.宁德志等[8]采用完全非线性边界条件的时域数学模型对纵摇容器中的液体晃荡运动进行研究,结果表明:相对于偶数阶固有频率来说,液体晃荡运动对奇数阶固有频率更为敏感.薛米安等[9]基于振动台对液舱晃荡运动进行实验研究,发现在波浪破碎等强非线性作用下,实际一阶共振频率大于理论推导的一阶固有频率.杨志勋等[10]采用缩尺比为1∶1、1∶2、1∶3,载液率为20%的系列GTT液舱,进行长时间激励下二维液舱晃荡运动尺度效应研究,结果表明:气液密度比是导致模型和原型结果之间存在较大差异的重要原因.
文中采用高精度全非线性Boussinesq型方程建立浅水液舱晃荡运动数值模型,并分析其在非规则外部激励作用下液舱内部晃荡运动特征,对深入理解非线性浅水液舱晃荡运动机理具有重要意义.
1 数值计算模型
选取长度为l、静水水深为h的二维矩形液舱,见图1.惯性坐标系oyz原点位于静水面中点,固定于大地上,z轴竖直向上.假定矩形水箱内为无旋无黏不可压缩流体,流场中速度势Φ满足下列条件:
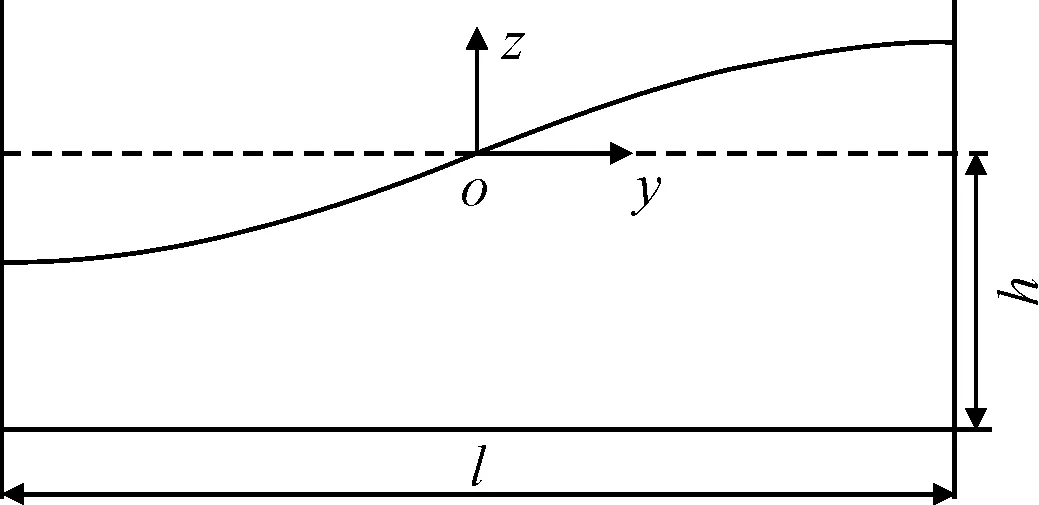
图1 二维液舱晃荡示意图
2Φ=0
(1)
(2)
ηt-Φz+ηyΦy=0z=η
(3)
(4)
随体坐标系固定于液舱上,随液舱一起运动.对于自由表面条件,将惯性坐标系下定义的时间导数通过以下表达式转化为随体坐标系下的时间导数.
(5)
(6)
故随体坐标系下的自由表面运动学和动力学边界条件为
ηt-v·η-Φz+ηyΦy=0z=η
(7)
(8)
本节后续方程均定义在随体坐标系下.
总速度势Φ分为两个部分:Φ=φ+φ,其中速度势特解φ满足拉普拉斯方程和物面不可穿透条件.若仅考虑横荡运动和升沉运动,那么
φ=yvb+zvc
(9)
另一部分速度势φ采用Boussinesq方程进行求解.
(10)
(11)
代入随体坐标系下自由表面边界条件可得:
ηt=v·η+Φz-ηy·Φy=
(12)
(13)

(14)
(15)
(16)
(17)
(18)
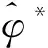
(19)
(20)
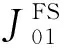
将式(19)和式(20)联立可得矩阵如下.
(21)
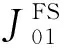
(22)
2 非规则激励计算方法
采用北海联合波浪谱(JONSWAP),其波能谱密度函数S(ω)表达式为
(23)
式中:
(24)
其中:ωp为JONSWAP谱图像峰值对应频率,当频率ω<ωp时,参数σ=0.07;当频率ω>ωp时,参数σ=0.09.参数γ取标准值3.3,参数Hs为有义波高,系数α的取值要保证等式(25)成立.横坐标为频率ω,纵坐标为谱密度S.
(25)
不规则激励由规则激励叠加获得,其位移和速度表达式为
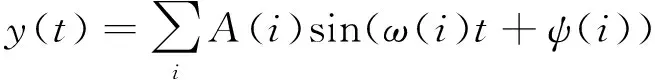
(26)
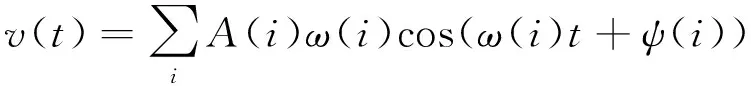
(27)
式中:A为幅值;ψ为随机相位.
A与谱密度函数S(ω)存在以下关系:
(28)
式中:Δω为频率间隔.
考虑到开始阶段速度变化过大,添加渐进函数f(t),对前五个谱峰周期进行修正,以保证计算结果的稳定性.
(29)
t0=10π/ωp
(30)
式中:t0为前五个谱峰周期.
则有最终结果如下.

(31)

(32)
舱内液体一阶固有频率(ω1=2.04 rad/s,根据色散关系式求得)作为谱峰频率,则有谱峰频率ωp=ω1=2.04 rad/s.频率ω取值范围为0.01~5 rad/s,频率间隔Δω=0.01 rad/s.参数γ取标准值3.3,有义波高Hs=0.012 m.波能谱密度函数S(ω)随频率变化(见图2),不规则速度激励图像见图3,并选取其中t=0~30 s表明渐进函数f(t)在前五个周期的缓冲效果(见图4).
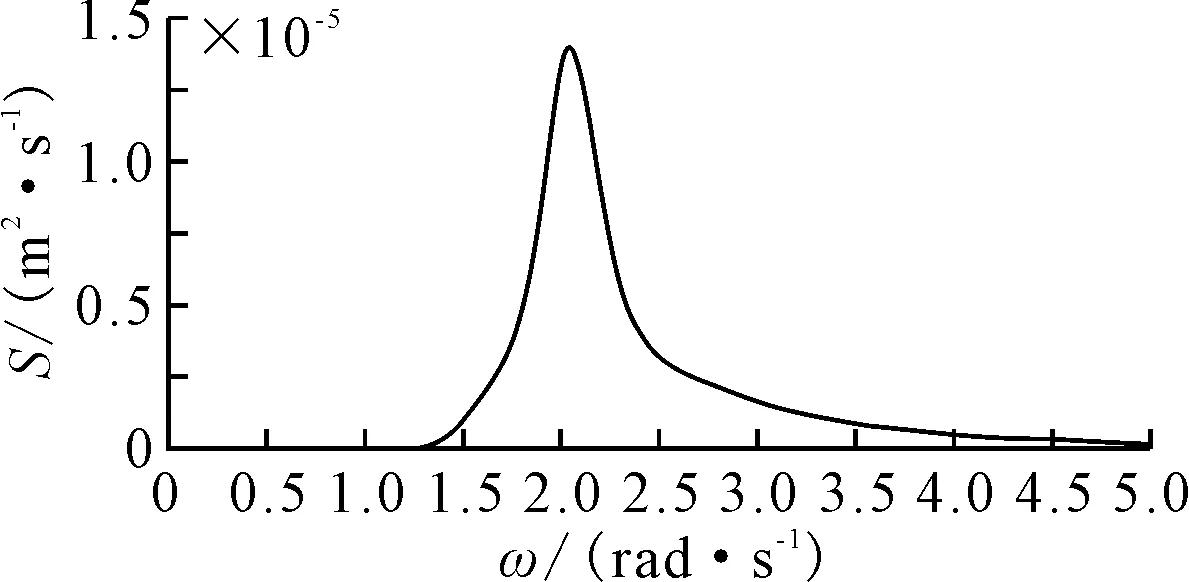
图2 波能谱密度函数S(ω)随频率变化图
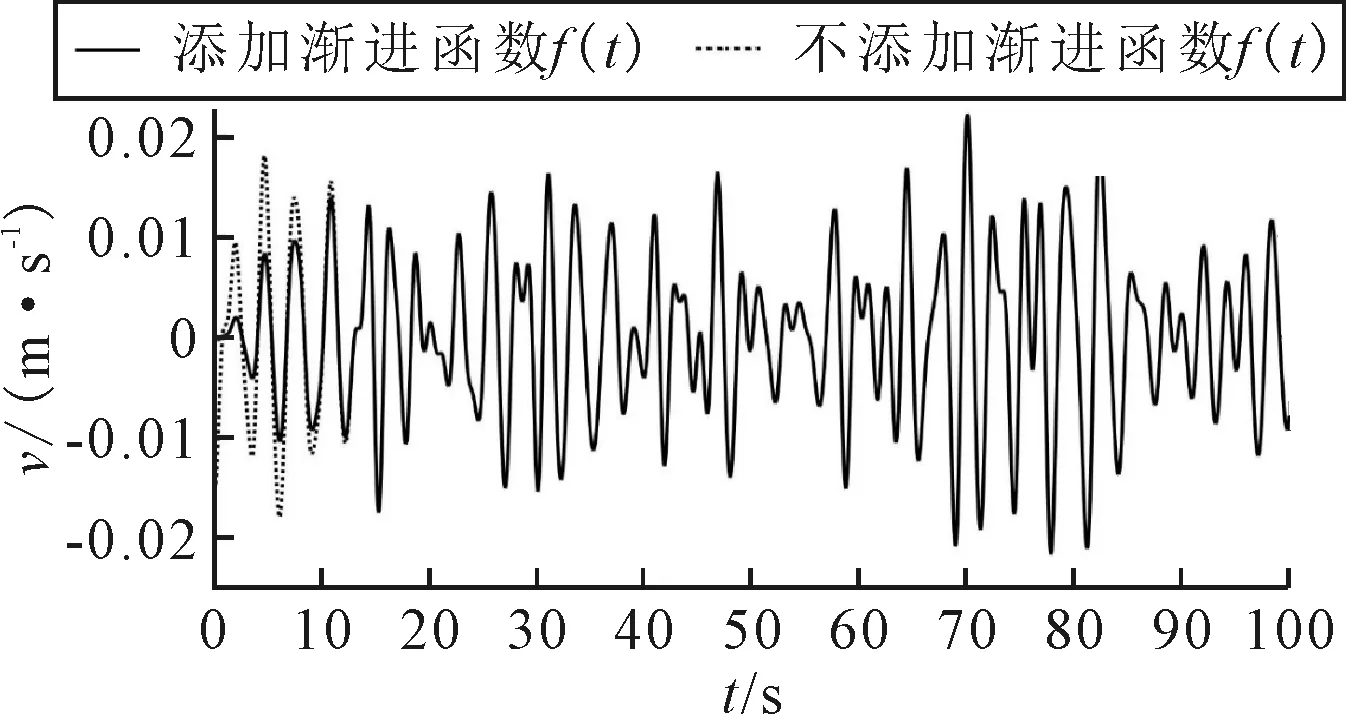
图3 不规则速度激励随时间变化图
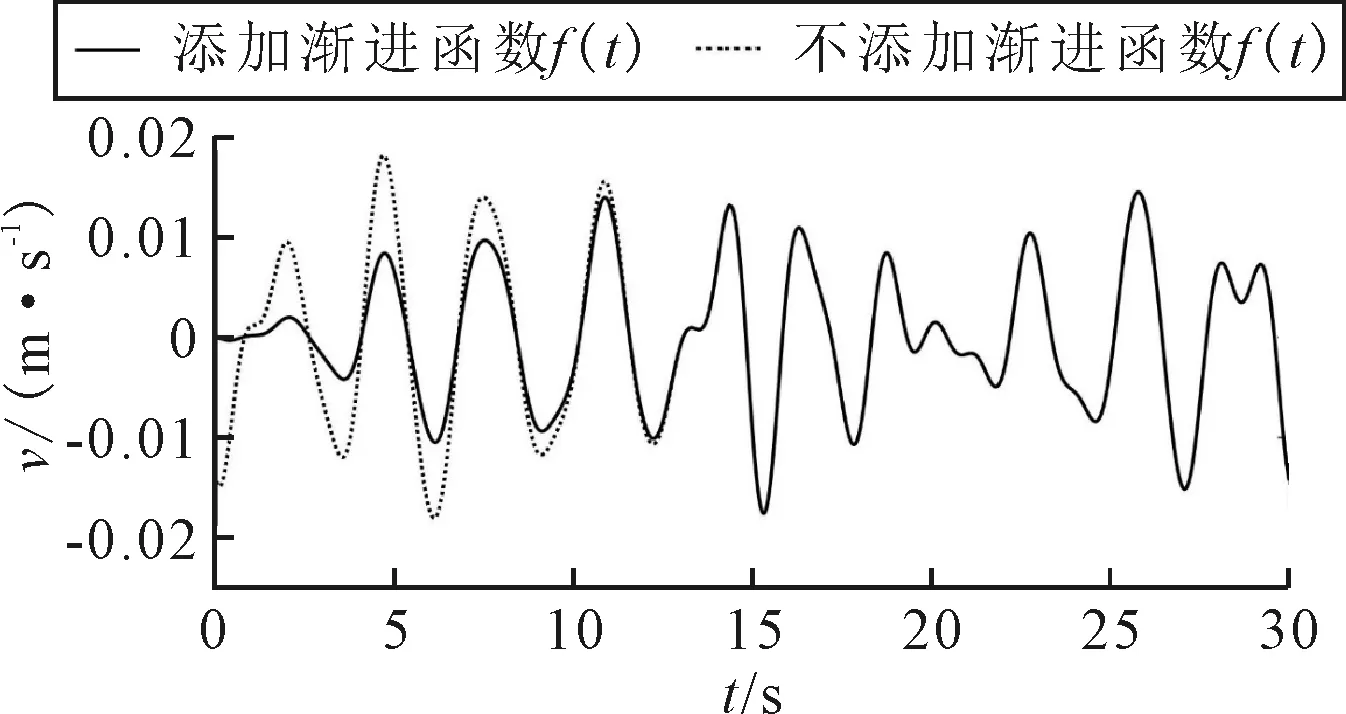
图4 不规则速度激励中添加与不添加渐进函数f(t)对比图
3 数值模拟结果
3.1 规则激励验证
为验证该数值模型的有效性,在相同工况下与文献结果(采用固有频率模块叠加求解方法)进行对比.二维矩形液舱长度L=1.175 m,水深h=0.06 m,受到长度方向简谐激励,激励幅值A=0.003 9 m.基于线性色散关系式获得液舱晃荡运动一阶固有频率ω1=2.04 rad/s,激励频率按文献选取ωp1=0.98ω1,ωp2=1.02ω1,ωp3=1.08ω1.
图5为激励频率分别为ωp1,ωp2,ωp3时二维液舱壁面处自由表面高度变化对比图,横、纵坐标分别为时间与激励周期之比t/T和自由表面高度与水深之比η/h.在激励频率ωp1=0.98ω1时,液舱中可以观察到三个行进波波峰在舱壁之间来回运动,舱壁处自由面波高时历曲线见图5a).在ωp2=1.02ω1和ωp3=1.08ω1时,液舱分别观察到两个行进波波峰和单个行进波波峰,自由面波高时历曲线见图5b)~c).由图5可知,文中所采用数值模型能准确地捕捉固有频率附近自由液面高度变化规律.

图5 舱壁处自由液面高度对比图
3.2 不规则激励数值模拟结果
基于色散关系式计算获得液舱晃荡运动一阶至五阶固有频率分别为ω1=2.04 rad/s,ω2=4.03 rad/s,ω3=5.93 rad/s,ω4=7.71 rad/s,ω5=9.34 rad/s.下面对海浪谱参数对液舱晃荡运动的影响进行研究,采用matlab进行数值模拟,程序运行时间t=600 s,网格点数取N=39(长度L=1.175 m),时间步长Δt=0.02 s,matlab自带能量谱密度函数pwelch函数对液舱舱壁处的自由液面高程时历曲线进行谱分析.
选取海浪谱谱峰频率ωp=ω1=2.04 rad/s,参数γ=3.3,有义波高Hs=0.008 m进行研究.图6为舱壁处自由液面高程时历曲线图,图6中自由液面高程变化整体呈现出不规则趋势.

图6 舱壁处自由液面高程时历曲线图(ωp=ω1)
改变海浪谱参数有义波高Hs的取值研究其对液舱晃荡运动的影响,图7为ωp=ω1=2.04 rad/s,参数γ=3.3,三种有义波高Hs舱壁处自由液面高程时历曲线谱分析图.由图7可知:三种工况下呈现出相似规律.波能谱密度图像谱峰频率位于一阶固有频率附近,其他阶固有频率附近存在部分波能,且表现出波能逐阶递减的趋势,在五阶固有频率之后波能可忽略不计.三种工况对比发现波能大小与有义波高成正相关,有义波高越大波能越大.
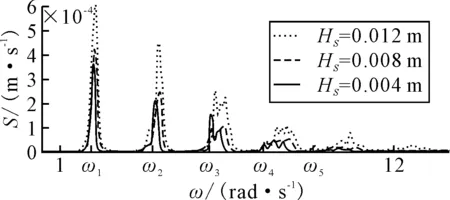
图7 不同Hs取值舱壁处自由液面高程时历曲线谱分析图
研究海浪谱谱峰频率ωp与液舱晃荡运动的关系,图8为海浪谱谱峰频率分别选取一阶至五阶固有频率ωp=ω1,ωp=ω2,ωp=ω3,ωp=ω4,ωp=ω5,参数γ=3.3,有义波高Hs=0.008 m时舱壁处自由液面高程时历曲线谱分析图.相对于偶数阶固有频率而言,液舱晃荡运动对奇数阶固有频率更加敏感,液舱晃荡运动波能主要集中于一、三、五阶.
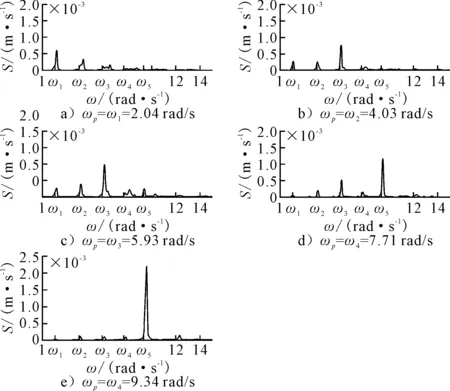
图8 不同ωp取值舱壁处自由液面高程时历曲线谱分析图
对谱峰频率不等于共振频率进行研究,以ωp=1.8 rad/s和ωp=2.3 rad/s为例(见图9),与一阶共振情况ωp=ω1=2.04 rad/s进行对比,参数γ=3.3,有义波高Hs=0.008 m.结果表明, 三种工况下谱分析图像呈现出类似规律,谱峰频率位于一阶固有频率附近,其他阶固有频率附近存在部分波能,且表现出波能逐阶递减的趋势.
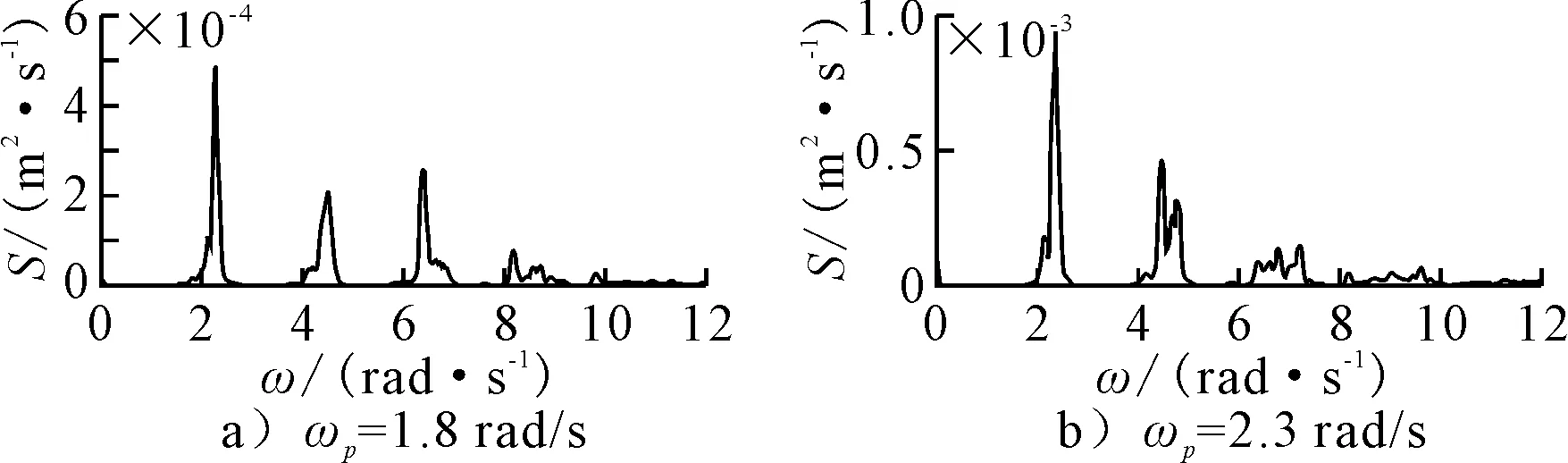
图9 舱壁处自由液面高程时历曲线谱分析图
4 结 论
1) 当谱峰频率等于一阶固有频率时,波能大小与有义波高大小成正相关,有义波高越大波能越大.当谱峰频率等于或偏离一阶固有频率时,波能主要集中于各阶固有频率附近,波能在一阶固有频率附近最大且从一阶至五阶波能逐渐降低,五阶以后可忽略不计.
2) 当谱峰频率等于二阶及以上固有频率时,浅水液舱晃荡波能集中于三阶或五阶固有频率附近.当谱峰频率为二阶、三阶固有频率时,浅水液舱晃荡运动波能均集中于三阶固有频率附近.当谱峰频率为四阶、五阶固有频率时,浅水液舱晃荡运动波能均集中于五阶固有频率附近.
