基于可能性理论的广义模糊数排序

张莹，叶国菊*，刘尉，赵大方

（1.河海大学理学院,江苏南京 210098；2.湖北师范大学数学与统计学院,湖北黄石 435002）

Zadeh[1]于1965年提出了模糊集理论。该理论可以更好地处理现实生活中的模糊问题，因此受到了人们的重视，并在各个领域得到了广泛的应用。在模糊集的应用中，如何对模糊数进行排序是一个重要的研究问题。在模糊数排序方法方面，已有很多学者提出在近似、决策、优化、预测等模糊应用系统中的方法[2−4]，而这些方法中所排序的模糊数的隶属函数为正规模糊数。在实际应用中，并不是所有问题都适合用正规模糊数进行描述，例如模糊数最大隶属度与1相差较大的情况。因此，Chen等[5]提出了应用更为灵活且具有高度的广义模糊数，高度为1时的广义模糊数即为正规模糊数。之后，许多学者开始研究广义模糊数，且广义模糊数在风险控制、决策过程、模式识别[6−7]等领域有着良好的研究前景。

另一方面，可能性理论[8]作为模糊决策理论的工具之一，在回归分析、聚类分析、结构优化、模糊逻辑、可能性决策、风险分析和数据融合方面有着广泛的应用[9−10]。1983年，Dubois等[11]首次将可能性理论用于模糊数排序，通过4个排序指标来确定两模糊数之间的大小关系。Lee 等[12]提出了基于模糊数的均值和离散度的模糊数排序方法，然而当模糊均值和模糊分布相同时，很难对其排序进行清晰的比较。Gu等[13]提出了一种基于可能性理论的广义模糊数排序方法，该方法利用可能均值与可能标准差之和对模糊数进行排序，较以往排序方法而言，计算简单且易于应用。当排序A1=[−8,−3],A2=[−6,−3]这两个区间模糊数时，通过该方法得到Mag(A1)=−3以及Mag(A2)=−3，即A1与A2相等，此结论与直觉不符。2021年，Liu 等[14]基于可能性理论，提出了广义模糊数排序的可能度公式，然而在可能均值与可能方差相同情况下，无法对广义模糊数做出合理区分。此外，在实际决策问题中，不同决策者对风险的态度是不同的，决策者风险态度反映着决策者的知识、背景和经验等，为使决策更加合理，在决策过程中应对决策者风险态度这一重要影响因素加以考虑。目前已有的模糊数排序方法中，鲜有提出将可能性理论与决策者风险态度综合考虑的方法，从而使得决策过程中丢失的信息比较严重，最终导致决策结果不理想。

鉴于以上情况，本文提出一种基于可能性理论和决策者风险态度的广义模糊数排序方法。该方法不仅能弥补已有方法的不足，并且计算简单，还可同时排序不同类型的广义模糊数。接着，利用数值例子与原有广义模糊数的排序方法作比较，以分析决策者风险态度对广义模糊数排序的影响。最后，采用该方法对上海银行间同业拆放利率所构成的模糊数进行排序，进一步验证本文所提出模糊数排序方法的合理性与有效性。

1 预备知识

本节给出模糊数理论与可能性理论的基本概念。

1.1 模糊数理论

1.2 可能性理论

2 基于可能性理论的模糊数排序方法

定义8对于一个广义L−R模糊数的大小定义为

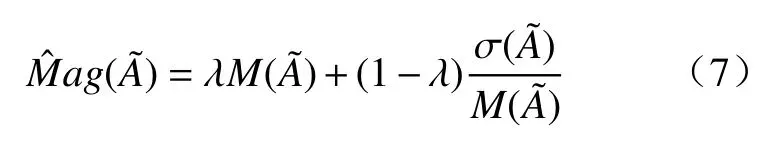
其中：λ∈[0,1]反映决策者的态度，当λ∈[0,0.5)时，决策者对决策事物持悲观态度；当λ=0.5时，决策者对决策事物持中立态度；当λ∈(0.5,1]时，决策者对决策事物持乐观态度。

下面本文通过数值例子的计算和对比分析，说明本文所提方法的合理性与有效性。

例1考虑下列4个广义三角模糊数：

具体如图1所示，试对其进行排序。

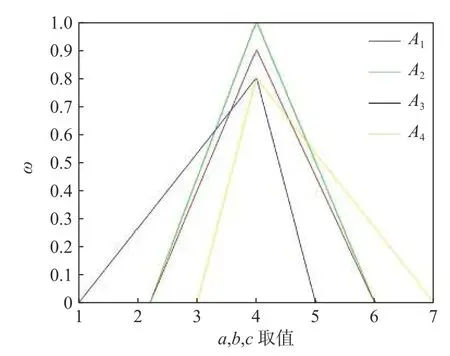
图1 广义三角模糊数

下面拟分两种情况考虑。

1)当决策者持乐观态度决策时（取λ=0.8），得到

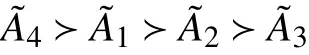
这个结果与文献[13]和文献[14]相同与文献[16]、[17]的最优、最劣结果相同。因此，本文所提出的方法在排序模糊数上是可行的。

2)当决策者持悲观态度决策时（取λ=0.1），得到

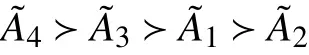
当决策者态度不同时，所得排序结果就会不同。由图1可知，有些模糊数差异并不是很明显，但由于本文所提出的方法考虑了决策者态度，使得结果更加全面，这可为做出不同决策提供较为全面的参考依据。因此，将决策者态度引入排序方法是合理的和必需的。

例2试排序下列两组模糊数：

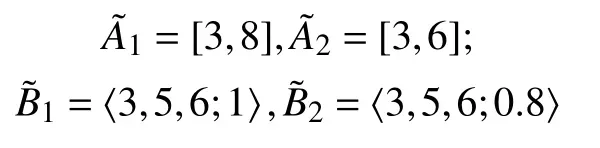
当λ=0.8，即决策者持乐观态度决策时，由式（7）得到

现在考虑下列模糊数：

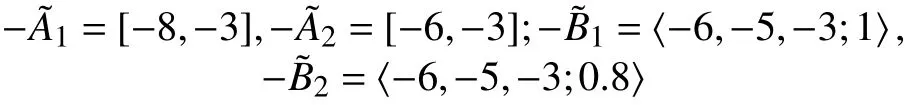
通过文献[13]中所提出的模糊数排序方法，得到

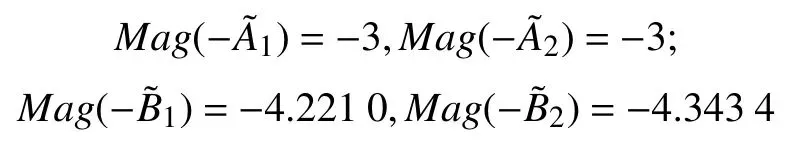
由此，得

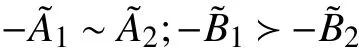
而由式(7),当λ=0.8，即决策者持乐观态度决策时，得到

注2由上述结果可得,通过文献[13]中所提方法无法区分以及不合理区分因此，本文所提出的方法在排序模糊数上是有效的。

例3考虑下列两组广义模糊数，分别对它们进行排序。

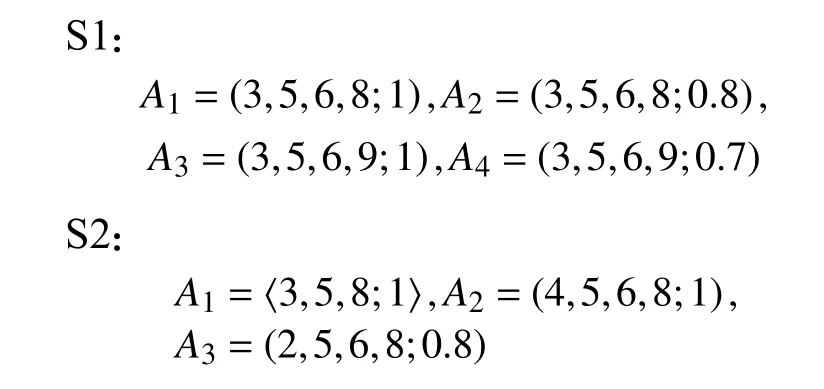
现通过不同方法对S1和S2进行计算，具体结果如表1所示。

表1 例3不同方法结果比较

由表1可知，通过这些方法得到的结果有一些是相互矛盾的，这一现象表明，模糊数排序是复杂的；在S1的所有结果中，我们可以看到排序结果并不稳定，但通过不同方法得到的最劣结果大多是A2，且本文能克服文献[16]中不能区分A1和A2的不足；在S2的所有结果中，我们可以看到A2永远是最优的，并且本文所提方法与文献[16]和文献[14]一致。

正如在前面的例子中所看到的，所提出的方法的主要优点是：它根据决策者风险态度提供了广义模糊数的合理全面的排序，并且容易计算、容易应用于实际问题。

3 实例分析

例4[18]上海银行间同业拆放利率(Shibor)是银行在上海批发(或“银行间”)货币市场上向其他银行提供无担保资金的每日参考利率。它是一种简单的、无担保的批发利率，由18家银行提供的利率计算而来，去掉4个最高和4个最低的利率，然后将剩下的10个利率取平均值。2014年前五个月的数据如表2所示。考虑到整个月指数的变化，它们被描述为模糊数，可视化数据如图2所示。Shibor作为货币市场参考利率，左右市场决策者的决策，从而间接影响了货币市场的发展。

表22014 年1月至5月上海银行同业拆息的模糊数，ω=1

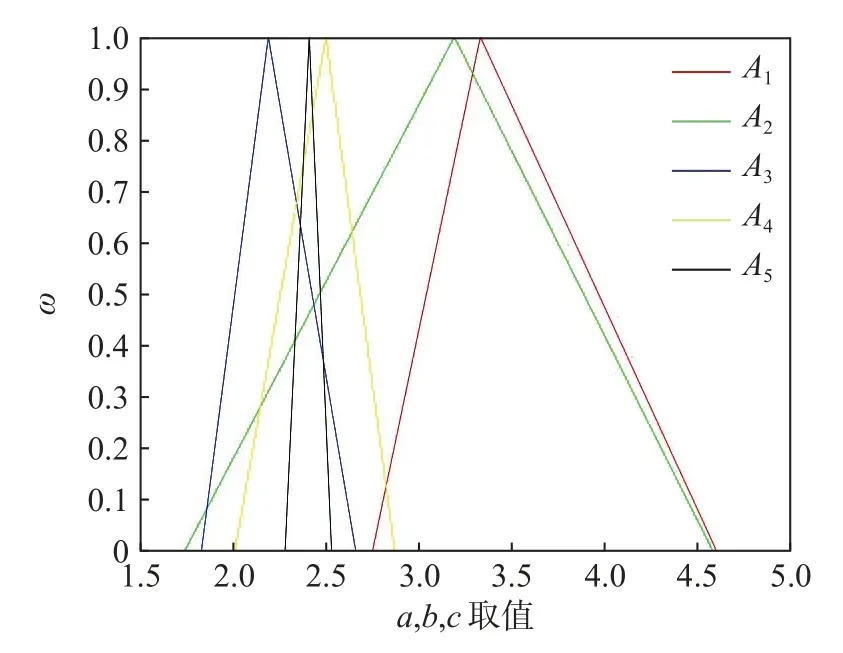
图22014 年1月至5月上海银行间同业拆放利率模糊数

当决策者持乐观态度时，取λ=0.8。

步骤1：由表1数据可知，表中为广义三角模糊数，计算广义三角模糊数的可能均值，得

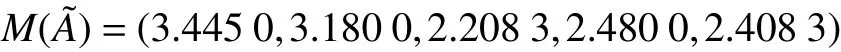
步骤2：计算广义三角模糊数的可能标准差，得

不同 λ取值时的结果，即决策者持不同态度时，所得结果不同，排序结果如表3所示。

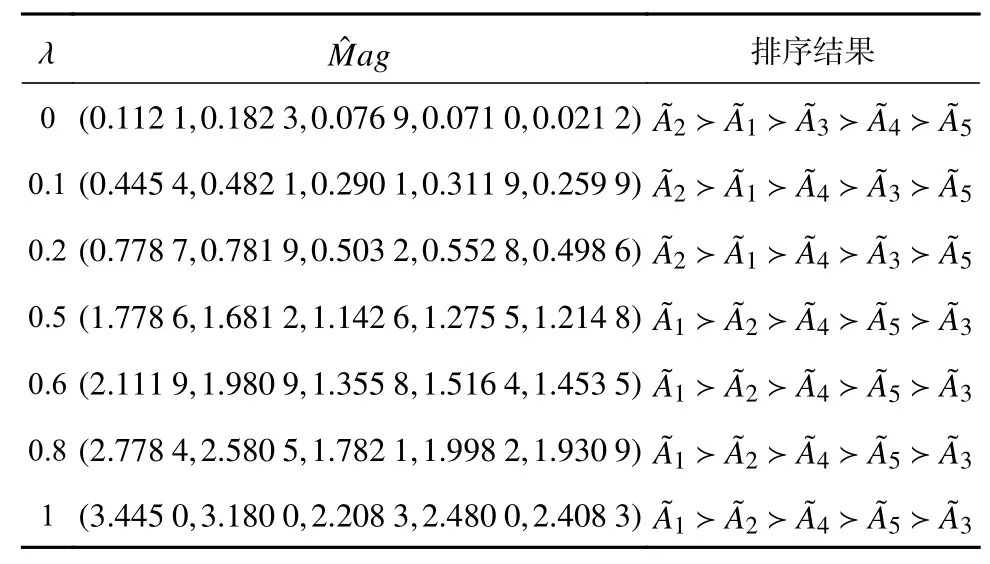
表3 不同λ取值时所得排序结果

由表3可知：当决策者持悲观态度（即λ<0.5，认为由Shibor促进市场发展稳健缓慢才是最好的）时，最优月份是二月；当决策者持中立与乐观态度（即，认为由Shibor促进市场迅速但不一定稳健发展是好的）时，最优月份是一月。

由此可见，在应用可能性理论对模糊数进行排序进一步达到决策目的时，考虑决策者态度的决策方法更全面合理而且与实际情况更吻合。

通过不同方法对银行5个月份的数据进行排序对比，排序结果如表4所示。

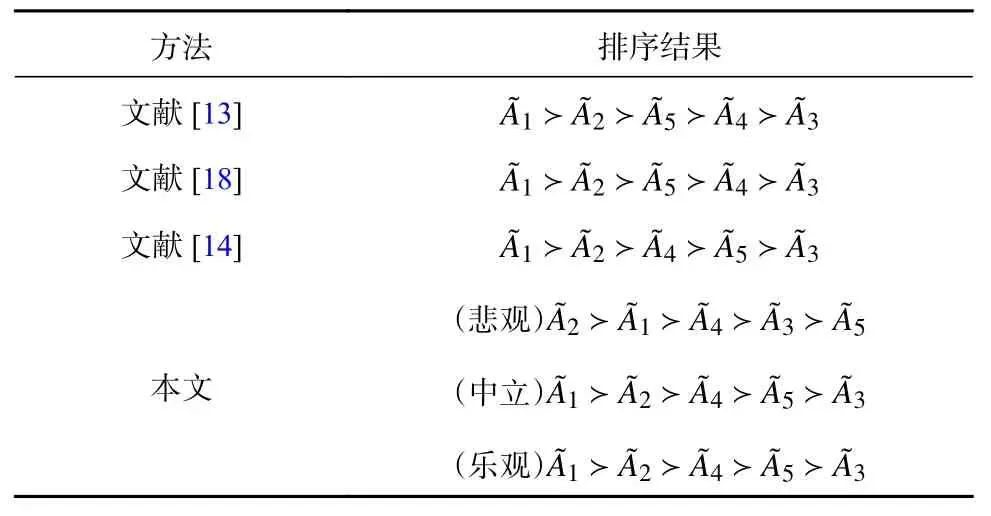
表4 不同方法所得排序结果

由表4可知：

1)文献[14]考虑到了可能均值比可能标准差更重要，所以文献[14]排序结果与本文决策者乐观时的排序结果一致；但是，由于本文引入变异系数与决策者风险态度，因此本文在排序时更加全面。

2)文献[13]与文献[18]排序最优结果与本文决策者乐观时的排序最优结果一致，都是一月，而它们之间的排序结果的不同主要体现在的顺序的不同。由图2可知，当排序施加决策者态度影响时，排序结果将有所不同。文献[13]与文献[18]没有考虑决策者态度，而本文的排序结果可以体现决策者态度对排序结果的影响。

4 结论

排序问题是模糊决策理论的核心内容之一，很多学者对此进行了广泛的研究。本文基于可能性理论，并考虑决策者风险态度，给出了排序广义模糊数的公式，并在此基础上提出了一种新的广义模糊数排序方法。该方法不仅有效利用模糊数在可能性理论方面的信息与决策者态度信息，还能弥补已有方法的不足，并且计算简单，可同时排序不同类型的广义模糊数。最后本文采用该方法对上海银行间同业拆放利率构成的模糊数进行排序，验证了本文所提广义模糊数排序方法的合理性和有效性。此外，该方法可以应用于各种决策模型和模糊应用系统。