高性能塑性铰RC墩柱损伤发展的数值模拟分析

罗星宇 孟庆利

(西南科技大学土木工程与建筑学院 四川绵阳 621010)

桥梁作为交通生命线的枢纽工程，其正常运营可充分发挥出交通生命线的运输功能。强震对桥梁的危害非常大，唐山地震、Loma Prieta地震、Northridge地震、阪神地震、汶川地震等均引发了桥梁倒塌、落梁，进而中断交通生命线[1]，造成了巨大的经济损失[2-4]。

为了避免桥梁倒塌，工程师们一般会采用延性设计方法对桥墩进行设计，在强震作用时桥墩上会形成塑性铰，这样可以耗散地震能量来降低动力响应。虽然采用这种设计可以在很大程度上避免桥梁倒塌，减轻生命财产的损失，但是桥墩往往会留下较大的残余位移，导致在震后难以恢复使用功能[5]，可能造成更大的经济损失[6-7]。基于此，众多学者[8-10]提出将纵筋从墩底断开，并在桥墩中穿过纵向无黏结预应力束，形成一种新型桥墩——摇摆桥墩。摇摆桥墩在侧向地震力作用下墩底与承台接触面可以提离，桥墩主要以刚体模态进行摆动，结构主体几乎不会受损，可实现震后快速恢复。然而，摇摆桥墩的震后可恢复功能对无黏结预应力束有一定的依赖性，在桥梁的长期运营中，防止预应力束腐蚀及预应力损失是一项困难的工作，受腐蚀的预应力束和预应力降低会降低桥梁的可靠度。

一些学者[11-15]研究了从另一个角度来增强桥梁震后可恢复功能的方法，即：在RC桥墩的潜在塑性铰区域设置高强度、高韧性的超高性能混凝土(UHPC)分段预制模板，同时对部分纵筋进行无黏结设计，以降低残余位移。这种设计可以有效防止在强震作用下RC桥墩塑性铰区域出现纵筋屈曲及大范围的混凝土压溃，进而增强桥梁的震后可恢复功能。Yamanobe等[12-13]对一种带有UHPC分段预制模板的RC桥墩进行了单向、双向伪静力试验及三向地震动模拟分析，发现其抗震性能较普通RC桥墩有明显提升。Ichikawa等[15]在此基础上进行了改进，增加了无黏结钢筋的数量，提出一种带有UHPC节段的抗震韧性桥墩，进行了双向伪静力及地震动加载试验。张兰芬等[11,14]提出一种高性能塑性铰(HPH)钢筋混凝土(RC)墩柱(RC bridge piers with high performance plastic hinges,HPHRC墩柱)并对其进行了伪静力试验。针对关键部件损伤，伪静力试验主要分析了钢纤维混凝土(SFRC)壳壁的宏观损伤发展，较少探究钢筋、SFRC壳壁及核心区混凝土的损伤发展及HPHRC墩柱的总体损伤发展，难以制定有针对性的改进措施以增强HPHRC墩柱的可恢复功能。

本文基于张兰芬等[11,14]开展的HPHRC墩柱伪静力试验的相关数据，建立了HPHRC墩柱的数值模型并验证了其有效性，分析了其在低周往复加载下关键部件的损伤发展及总体损伤发展，为后续改进提供参考。

1 HPHRC墩柱数值模型的建立及验证

为了分析HPHRC墩柱在低周往复加载下的损伤发展，首先建立了HPHRC墩柱的数值模型，然后对比了数值模拟和试验两种不同方法得到的滞回曲线、骨架曲线及割线刚度曲线，验证了数值模型的有效性并给出了模拟与试验结果存在差异的可能原因。

1.1 数值模型建立

数值模型的建立涉及模型尺寸和混凝土、钢筋及其相互作用三者的本构模型、单元、力学参数设置，还有墩柱边界条件和加载规则。

通过伪静力试验发现，距离HPHRC墩柱基座底部250～650 mm高度范围内非线性程度较高，故该区域内的混凝土(包括普通混凝土和SFRC)采用损伤塑性模型[16]，距离基座底部650～1 450 mm高度范围内的混凝土采用线弹性本构模型，如图1所示。在数值模型中，箍筋仅布置在距基座底部250～650 mm高度范围内；纵筋和无黏结钢筋仅布置在距基座底部125～775 mm高度范围内。关于HPHRC墩柱的详细信息可从文献[14]获取。

图1 HPHRC墩柱数值模型Fig.1 Numerical model of the HPHRC pier

墩身普通混凝土的单轴本构关系参考文献[17]，SFRC的单轴本构关系参考文献[18-20]。墩身普通混凝土的受压损伤因子根据Sidiroff能量等价原理计算得到[21]，受拉损伤因子根据拉伸塑性应变与开始卸载时的拉应变比例为0.1计算得到[22]。普通混凝土及SFRC采用八结点六面体减缩积分实体单元。为了避免数值求解时产生非正塑性应变而导致计算终止，普通混凝土及SFRC的弹性模量由抗拉强度比峰值拉应变得到，基座普通混凝土、墩身普通混凝土、SFRC的弹性模量计算值分别为3.400×104，2.144×104，4.381×104MPa。普通混凝土的轴心抗压强度计算值采用立方体抗压强度试验值的0.8倍[17]，具体为17.808 MPa；轴心抗拉强度通过立方体抗压强度试验值计算得到[17]，为2.06 MPa。SFRC的轴心抗压强度采用试验值67.74 MPa，轴心抗拉强度计算值采用劈裂抗拉强度试验值的0.9倍[23]，为11 MPa。

纵筋、无黏结钢筋采用二折线强化弹塑性本构模型，设置Von-Mises塑性屈服准则及随动强化准则；箍筋采用二折线理想弹塑性本构模型，设置Von-Mises塑性屈服准则及各向同性强化准则。纵筋采用八结点六面体减缩积分实体单元，无黏结钢筋及箍筋采用两结点桁架单元。直径12 mm的HRB335级纵筋，屈服强度354.87 MPa，极限强度 660.49 MPa，断后伸长率为0.25；直径10 mm的HPB300级无黏结纵筋，屈服强度333.06 MPa，极限强度623.7 MPa，断后伸长率为0.29；直径2.5 mm的钢丝箍筋，屈服强度267.87 MPa。钢筋的弹性模量2.1×105MPa，屈服应变及极限应变采用计算值，屈服应变根据屈服强度比弹性模量得到，极限应变采用钢筋的断后伸长率。

基座表面与SFRC壳壁表面、SFRC壳壁表面之间、SFRC壳壁表面与距离基座底部650 mm处混凝土表面的接触选择切向摩擦和法向硬接触[24],切向摩擦系数设置为0.5。SFRC壳壁表面与核心区混凝土表面之间的相互作用采用损伤内聚力模型[24]，核心区混凝土的抗剪强度采用2.29 MPa，计算参考文献[17]。纵筋通过Tie方式与混凝土产生相互作用，无黏结钢筋两端通过Embedded方式嵌入基座和墩身。考虑箍筋约束效应，箍筋通过Embedded方式嵌入墩身[24]。

墩柱底部设置固结边界条件，墩顶设置简支边界条件。竖向加载规则为在墩顶施加200 kN竖向集中力并在加载过程中保持力不变，水平加载规则参考文献[14]，为了提高模拟计算效率，每个位移工况仅加载一圈。

1.2 数值模型验证

如图2(a)所示，HPHRC墩柱的模拟滞回曲线与试验滞回曲线大致吻合，差异较大处在滞回曲线的反向加载段，模拟曲线相比试验曲线更为饱满；模拟曲线加载段的切线刚度显著提高，所对应的位移集中在0～24 mm位移范围内，而试验曲线与之相比则更为分散。对比骨架曲线及割线刚度曲线发现，除了位移加载初期的几个工况外，其余工况下模拟曲线和试验曲线的差异在25% 以内，吻合度较高，如图2(b)、图2 (c)所示。除此之外，还对比了试验和模拟结果(见图5)的SFRC壳壁损伤，损伤集中在墩底壳壁上，二者损伤结果较为接近。限于篇幅，这里不展示伪静力试验的损伤，具体可查看文献[14]。

图2 HPHRC墩柱低周往复加载结果对比Fig.2 Comparison of cyclic loading results for the HPHRC pier

数值模拟结果与试验结果存在一些差异的原因：(1)试验时由于加载连接并非理想固结，可能导致数值模型的初始刚度比实际刚度大；(2)在SFRC本构模型中，双/单轴抗压强度的比值采用默认值可能导致SFRC的多轴抗压强度比实际值大，造成模拟曲线承载力更高；模拟中并未在纵筋本构中设置下降段，这可能导致模拟的骨架曲线下降较缓慢；(3)未考虑纵筋和混凝土之间的黏结失效以及循环加载引起的钢筋力学性能降低，这可能导致滞回曲线的加载及反向加载段存在一定差异。

2 HPHRC墩柱损伤发展的数值模拟分析

首先分析了钢筋、SFRC壳壁、核心区混凝土的损伤发展，然后结合这些部件的损伤分析了HPHRC墩柱的总体损伤发展。

2.1 钢筋的损伤发展

2.1.1 钢筋屈服

如图3所示，正负两种工况下纵筋及无黏结钢筋的屈服位移较为接近，故仅对正向进行分析。在正向3.6 mm(0.3%)时，第4排纵筋屈服；正向5.8 mm(0.4%)时，受拉纵筋(第2排、第3排、第4排纵筋)屈服；正向26.6 mm(2.2%)时，所有纵筋屈服。对于无黏结钢筋，在正向3.6 mm(0.3%)时，第6排无黏结钢筋屈服；正向18.3 mm(1.5%)时，受拉无黏结钢筋(第2排-第6排无黏结钢筋)屈服；正向38.6 mm(3.2%)时，所有无黏结钢筋屈服。

图3 墩底截面钢筋在正负向工况下的屈服位移Fig.3 Yielding displacement of bars in the bottom section under positive and negative displacement cases

由于无黏结钢筋的应变沿纵向长度均匀分布，在截面位置与纵筋接近情况下，其应变更小，屈服所需位移较大。例如在正向工况下，第3排、第4排无黏结钢筋的屈服位移分别是第2排、第3排纵筋屈服位移的1.75倍和1.40倍。

2.1.2 钢筋应变发展

为了分析在低周往复荷载作用下HPHRC墩柱钢筋的应变发展情况，需要借助应变包络曲线。钢筋的应变包络曲线可以展示出钢筋在每一工况下的最大应变，从而掌握钢筋的应变发展情况。提取应变滞回曲线中每一个工况峰值位移对应的应变即可得到应变包络曲线。墩底截面钢筋的应变包络曲线如图4所示。

从图4可以看出，虽然墩底截面纵筋和无黏结钢筋的应变都随着位移的增大而增大，但是纵筋的应变增加速度更高。在正向60 mm工况(5%)时，第4排纵筋的应变达到极限应变的90%，接近断裂；第6排无黏结钢筋的应变约为极限应变的12%，还有较大的耗能空间未被利用。

综上所述，纵筋较大的塑性应变会导致HPHRC墩柱的可恢复功能不足，这不利于震后地震灾区交通的快速恢复。

2.2 SFRC壳壁的损伤发展

从图5可以看出，在正向60 mm工况(5%)下，损伤主要集中在墩底SFRC壳壁两侧的50 mm×400 mm矩形区域内，而墩底壳壁的损伤主要集中在靠近基座的30 mm高度范围内，所以选取最靠近基座的一层单元进行应变和应力分析。由于正负工况下损伤基本一致，所以以正向工况为例进行分析。

从图6(a)可以看出，随着水平位移的增大，墩底壳壁受压边缘0～20 mm范围内单元的应变均呈现出单调增大趋势，20～50 mm范围内单元的应变呈现出先增大再减小最后又增大的规律，这与中性轴的位置变化有关。正向20 mm工况时，壳壁受压边缘0～10 mm范围内的单元压应力达到峰值，此后随着位移的增大，该范围内的SFRC出现压碎现象，压应力逐渐降低，如图6(b)所示；正向36 mm工况(3%)时，距离壳壁受压边缘10～20 mm范围内SFRC的压应力达到峰值；此后随着加载的继续，壳壁压碎区域扩展至0～20 mm范围内；当水平位移达到60 mm(5%)时，距离壳壁受压边缘20～50 mm范围内的单元压应力仍未出现下降趋势，说明其仍然具有较大的承载潜力。值得注意的是，壳壁除了受压之外，壳壁与核心区混凝土接触的部位会产生切应力，这是由于核心区混凝土的边缘受拉时，将部分剪力传递给壳壁导致的，如图5(b)所示。

图5 正向60 mm工况下SFRC壳壁损伤Fig.5 Damage of SFRC segments under displacement of 60 mm

图6 墩底SFRC壳壁受压侧0～50 mm 范围内单元的应变、应力包络曲线Fig.6 Strain-displacement and stress-displacement envelope curves of elements within the section range of 0-50 mm of the bottom SFRC segment on the compression side

2.3 核心区混凝土的损伤发展

2.3.1 核心区混凝土开裂

如图7(a)、图7(b)所示，在正向60 mm工况(5%)下，在距离墩底0～125 mm高度范围内，核心区混凝土的主拉应变较大，其中墩底受拉边缘处单元的主拉应变最大，达到了0.4，截面受拉边缘开裂非常严重。

图7 正向60 mm工况下核心区混凝土的损伤Fig.7 Concrete damage in core area under displacement of 60 mm

为了展示核心区混凝土墩底截面的应变发展过程，选取第1排-第5排、第10排、第15排、第19排单元进行分析，各排单元的位置如图8所示。根据图9的应变数据可知，4 mm工况时，核心区混凝土墩底截面开裂就非常严重了，截面受压单元为第1排-第3排，截面大部分区域已经开裂，当水平位移为 -4 mm时墩底已经形成贯穿裂缝。16 mm工况之后，核心区混凝土的墩底截面仅第一排单元受压，墩底截面的开裂进一步加重。

图8 墩底截面核心区混凝土单元编号Fig.8 Numbering of elements in the bottom section of concrete in core area

图9 核心区混凝土墩底截面单元的应变包络曲线Fig.9 Strain-displacement envelope curves of elements in the bottom section of concrete in core area

2.3.2 核心区混凝土压碎

核心区混凝土的损伤除了开裂之外，还有压碎，但是其压碎区域较小，主要集中在靠近边缘的10 mm范围内。由于正负不同工况下损伤情况相差不大，所以以正向工况为例进行分析。

从图7(c)可以看出，正向60 mm(5%)工况时，距离墩底0～75 mm高度范围内，混凝土的压应变较大，其中墩底压应变最大，所以取墩底截面靠近受压侧混凝土单元的应变及应力数据进行分析。从图10可以看出，墩底截面靠近核心区受压边缘的第1排混凝土单元在所有正向工况下均受压，在正向12 mm(1%)工况时压应力达到峰值，此后呈现下降趋势，逐渐压碎；第2排混凝土单元在正向8 mm(0.67%)工况之后逐渐开始受拉，这是因为SFRC壳壁单元的压应力逐渐增大，中性轴向受压侧移动；第3排混凝土单元在正向4 mm(0.33%)工况之后逐渐开始受拉，同样是由于中性轴向受压侧移动引起的。另外，对比图10(b)和图6(b)中混凝土单元压应力首次下降时对应的位移可知，核心区混凝土会比SFRC壳壁更早压碎，这可能与二者的抗压强度大小及HPHRC墩柱配筋面积大小有关。

图10 核心区混凝土墩底截面受压侧单元的应变、应力包络曲线Fig.10 Strain-displacement and stress-displacement envelope curves of elements near the compression edge in the bottom section of concrete in core area

2.4 SFRC 墩柱的总体损伤发展

根据各关键部件的损伤情况，HPHRC墩柱的总体损伤发展可分为A，B，C，D 4个不同阶段，如图11所示。下面将结合关键部件的损伤对HPHRC墩柱的总体损伤发展进行分析，关键部件在不同阶段中的损伤情况见表1。

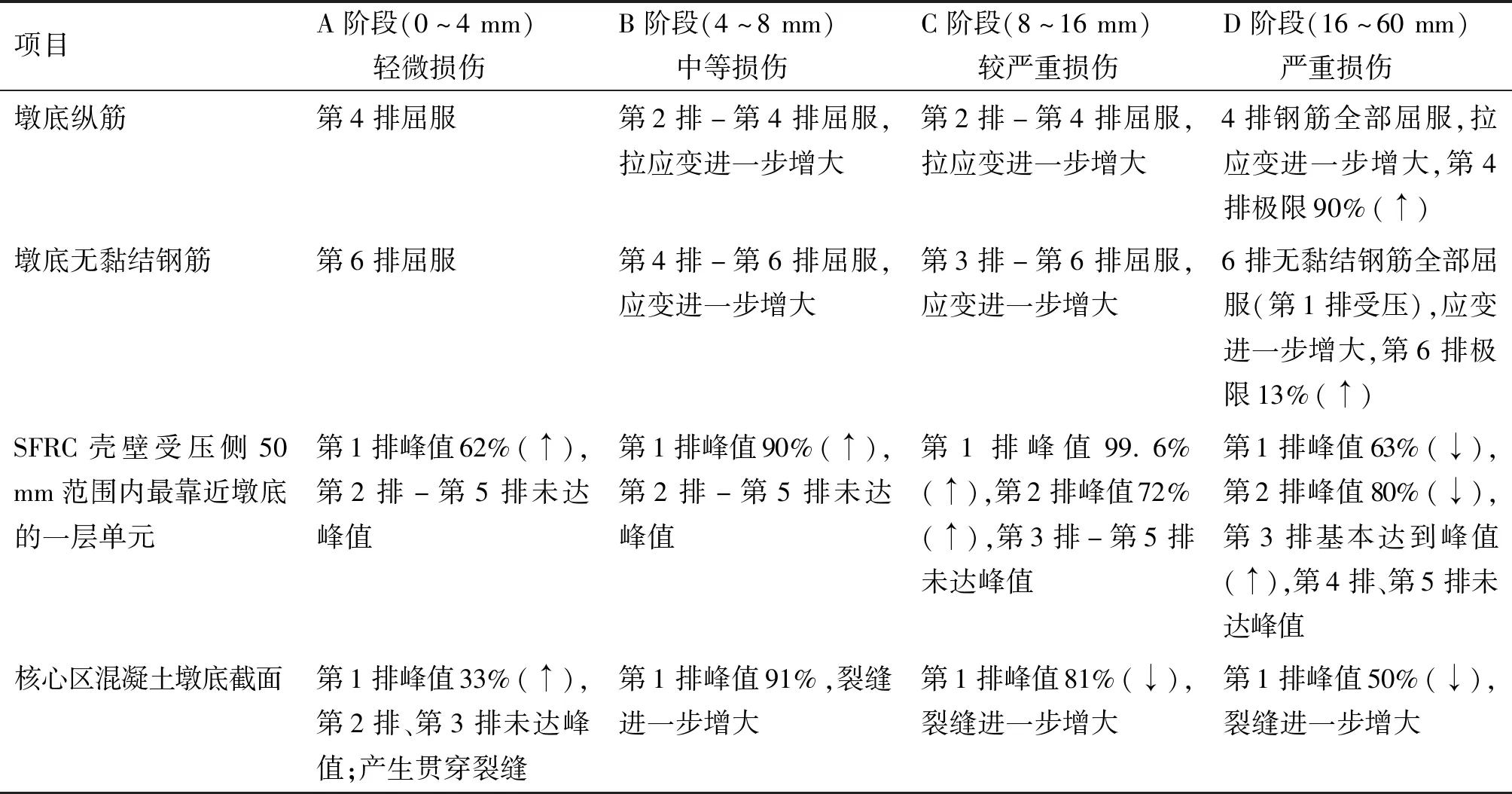
表1 关键部件在不同阶段中的损伤情况Table 1 Damage details of critical parts of the HPHRC pier in different stages

图11 HPHRC墩柱的总体损伤发展Fig.11 Overall damage progression of the HPHRC pier

A阶段(水平位移0～4 mm)中，墩底截面的最外层钢筋屈服；SFRC壳壁和核心区混凝土基本处于受压弹性状态，核心区混凝土开裂较为严重，仅3排单元受压，其余均受拉开裂；墩柱整体处于轻微损伤状态，骨架曲线的切线斜率较大。

B阶段(水平位移4～8 mm)中，墩底截面纵筋及无黏结钢筋的应变进一步增大，钢筋的非线性程度总体较低；SFRC壳壁和核心区混凝土的受压边缘处单元达到峰值压应力的90%，墩底截面核心区混凝土开裂加重；墩柱处于中等损伤状态，骨架曲线的切线斜率相对A阶段明显降低。C阶段(水平位移8～16 mm)中，墩底截面纵筋及无黏结钢筋的应变进一步增大，纵筋的非线性程度中等，无黏结钢筋非线性程度较低；SFRC壳壁受压边缘处的单元达到峰值压应力，核心区混凝土受压边缘处的单元压碎，压应力略微下降，墩底核心区混凝土非常接近全截面受拉状态；墩柱处于较严重损伤状态，骨架曲线的切线斜率相比B阶段明显下降，当水平位移为16 mm时，达到峰值承载力。

D阶段(水平位移16～60 mm)中，墩底截面纵筋及无黏结钢筋的应变进一步增大，纵筋的非线性程度非常高，接近断裂，而无黏结钢筋的非线性程度相对较低；SFRC壳壁压碎区域进一步扩大，当水平位移为60 mm时，壳壁受压边缘20 mm范围内的SFRC被压碎，核心区受压边缘约10 mm范围内的混凝土被压碎，墩底截面核心区混凝土应变进一步增大，墩柱处于严重损伤状态，承载力开始下降。

3 结论

采用数值模拟方法对HPHRC墩柱在低周往复加载下的损伤发展进行了分析，主要结论如下：(1)有黏结钢筋应变发展程度较大，当位移角达到 0.48% 时，墩底最外侧的3排有黏结钢筋全部屈服；当位移角达到5% 时，墩底最外侧有黏结钢筋接近断裂；墩底受拉有黏结钢筋的塑性应变较大，难以修复。(2)无黏结钢筋的应变发展程度显著低于有黏结钢筋，当位移角达到1.5% 时，最外侧的5排有黏结钢筋全部屈服；当位移角达到5%时，前者的最大应变约为后者的1/5，但其仍显著大于屈服应变，对墩柱自复位有一定影响，同时给修复带来一定困难。(3)SFRC壳壁的受压损伤主要集中在最底部壳壁上；当位移角达到1.7%时，墩底壳壁受压边缘达到峰值应力。当位移角达到5%时，墩底壳壁单侧压碎宽度约为20 mm。(4)核心区混凝土开裂较为严重，受压损伤可忽略。当位移角达到 0.3%时，墩底截面产生了贯通裂缝，此后随着加载进行，开裂逐渐加重；当位移角达到1%时，墩底混凝土仅受压边缘达到峰值压应力；当位移角达到5%时，两侧受压边缘各约10 mm范围内的混凝土压碎，各仅占核心区截面高度的1/30。(5)结合各关键部件的损伤发展可知，HPHRC墩柱的总体损伤发展可分为4个阶段：A阶段，HPHRC墩柱处于轻微损伤状态；B阶段，HPHRC墩柱进入屈服，处于中等损伤状态；C阶段，HPHRC墩柱达到峰值承载力，处于较严重损伤状态；D阶段，HPHRC墩柱承载力开始下降，处于严重损伤状态。HPHRC墩柱的损伤主要为核心区混凝土开裂及纵向钢筋存在较大塑性应变，故其可恢复功能有所欠缺，建议采用高延性材料及参数化分析进行优化改进。