考虑不确定性的供应链可靠性优化设计

闫 英 锁 斌 何晓兰

(1.西南科技大学经济管理学院 四川绵阳 621010；2.西南科技大学信息工程学院 四川绵阳 621010)

随着市场竞争日益加剧，目标客户对产品响应时间的要求越来越高，而分工的精细化和专业化也使得供应链越来越复杂，更容易受到各种不确定性因素的干扰。供应链的抗冲击、抗风险、稳定运作能力已成为供应链企业的核心竞争力之一。如何诊断、分析、设计并提高供应链的可靠性受到了国内外学者的广泛关注[1-8]。

在工程可靠性领域，“可靠性是设计出来的”这一理念已得到广泛认同，可靠性优化设计研究受到了高度重视[9-11]。同样，对于供应链来说，其可靠性也依赖于系统规划和设计阶段供应链系统的构建和配置。目前国内在供应链可靠性优化设计方面做了一些初步探索。余小川等[12]研究了串并联逻辑结构对物流系统可靠性的影响，并对有约束下的物流系统成本优化问题进行了初步探讨；张德海等[13]研究了基于故障树的物流服务供应链可靠性指标分配方法，并以汽车整车物流服务供应链为对象建立了服务能力优化模型；郑哲文[14]采用模糊层次分析法研究了应急供应链系统的可靠性设计；陈德良等[15]研究了可靠性约束下的物流中心选址问题，并采用改进的遗传算法求解。总的来说，目前国内在供应链可靠性优化设计方面的研究还很不成熟，尤其是以上研究均未考虑到供应商供应能力的不确定性和采购价格的不确定性。本文将在充分考虑这些不确定性因素的情况下研究制造商(核心企业)与供应商构成的两级供应链的可靠性优化设计问题，构建更加实用的最优化模型，以期在满足可靠性要求的前提下达到最优成本。

1 问题描述

本文研究由一个制造商(核心企业)和多个供应商组成的两级供应链系统。设制造商需要采购m种类型的零配件，每种零配件都有Ni(i=1,2,…m)个供应商，第i种零配件的供应商记为Si1,Si2,…SiNi。若将供应链失效定义为顶事件，则当任何一种零配件的供应环节失效，则供应链失效，因此各个零配件供应环节之间为串联关系；零配件i供应环节中有Ni个供应商共同为制造商供货，单个供应商失效不一定会导致供应链失效，因此供应商之间为并联关系。据此，可构造由制造商和多个供应商组成的两级供应链模型，如图1所示。

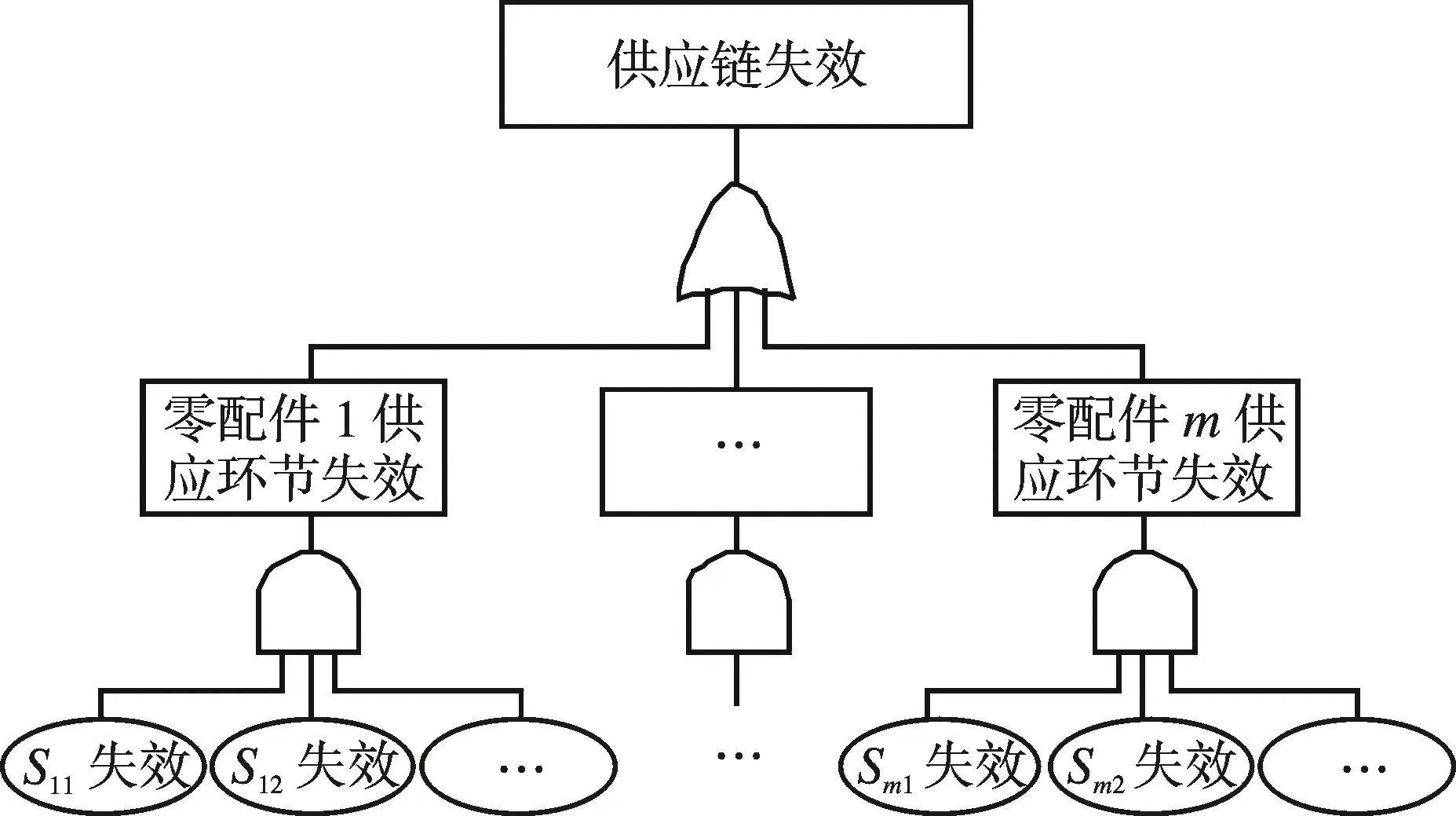
图1 两级供应链模型Fig.1 Two-level supply chain model

(1)

零配件i供应环节的可靠度为Ri，则整个供应链的可靠度为：

(2)

由图1可知，供应商的数量Ni越大，可靠度R0越高；同时，由于单个供应商的采购数量下降，单价Pi必然会增加，总成本C也会增大。供应链由m个供应环节组成，每一个环节的可靠性都会影响到供应链整体可靠性。对于可靠度较低的单元供应商，通常需要提高并联单元的数量来保证供应链整体可靠度，但同时也会增加成本。由式(2)可知，降低某些成本较高的供应环节的可靠性，同时增加其他成本较低环节的可靠性，同样可以保证整个供应链的可靠性水平，而且可获得更低的成本。因此，如何合理选择供应商的数量，构建既满足可靠性要求、又能达到最低成本的供应链，是一个值得研究的问题。

2 供应链可靠性优化设计

2.1 可靠性优化设计模型

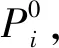
(3)

其中δi为常数，表示零配件i的单价修正参数。

(4)

为便于讨论，假设Ni个供应商的供应能力相同，则由(4)式可得：

(5)

由式(5)可知零配件i供应环节的可靠度Ri是Ni的函数。

在可靠度约束下，就需要优化供应链结构，确定各个供应环节最优的供应商数量N=(N1,N2,…Nm)，从而使供应链达到最低的成本。因此提出以下供应链可靠性优化设计模型：

(6)

2.2 可靠性优化设计模型求解

式(6)的最优化问题难以直接用解析的方法求解，因此采用以下数值仿真的方法来搜索最优解。

步骤1：设搜索次数初值L=1，初始供应商数量为N(1)=(N1,N2,…Nm)=(1,1,…1)，带入式(2)-式(6)计算R(1)和C(1)。若R(1)≥R0，则N(1)即为最优供应商数量，C(1)即为最优成本，结束；否则转步骤2。

步骤2：通过重要度分析确定需要增加供应商的环节k。一般来讲，供应链的成本和可靠度都非常重要，成本是越低越好，可靠度则是越高越好，因此以第i个供应环节增加1个供应商后的可靠度增量与成本增量倒数的乘积作为该供应环节的综合重要度系数：

(7)

其中，ΔRi表示可靠性重要度，且

(8)

ΔCi表示成本重要度，且

(9)

记

k=index(max(Ii|i=1,2,…m))

(10)

则第k个供应环节需要增加1个供应商，即Nk=Nk+1，L=L+1，转步骤3。

步骤3：根据式(4)-式(6)计算R(L)和C(L)。若R(L)≥R0，则N(L)即为最优供应商数量，C(L)即为最优成本，结束；否则转步骤2。

值得注意的是，在以上算法中，刚开始搜索时Ri(i=1,2,…m)和R可能很小(趋近于0)，由于计算机浮点数存储精度的原因，Ri和R的计算结果会为0，当Ri首次大于0时，搜索算法会陷入局部最优，始终停留在第i个零配件供应商。为避免这一问题，设置一个门限值ε，按如下方法改进搜索算法：

if in(Ri)≤ε

k=index(min(Ri|i=1,2,…m))

else

k=index(max(Ii|i=1,2,…m))

end

Nk=Nk+1

ε可取(0,0.5)之间的值，可以很好避免陷入局部最优的问题，较快收敛到全局最优解。

3 实例分析

某制造商和5类零配件供应商构成的供应链，为了获得更大的市场竞争优势，需要在保证一定可靠度的前提下尽量节约成本。设制造商对5类零配件的月需求数量(单位：件)分别为800，400，500，900，300，单个供应商月采购数量分别低于300，200，200，500，200时的基本单价(单位：元/件)分别为50，60，40，70，130，单价修正参数(单位：元/件)分别为2，3，4，5，17，每类零配件有若干个供应商可选择。受原材料采购和生产因素的影响，各类零配件供应商的供应能力服从正态分布，分布参数如表1所示。现需要确定5类零配件供应商的最优数量，从而使供应链满足0.96的可靠度且成本最低。

表1 供应商供应能力的分布参数Table 1 Distribution parameters of supplier’s supply capacity

从初始数量(1,1,1,1,1)开始搜索，设门限值ε=0.01，当首次出现min(R1,R2,…R5)>ε时，供应商数量为(2,1,2,2,1)，此时综合重要度系数为I=10-3×(0.0116 0.8258 0.0000 0.2125 0.0044)

因此k=2，需要在第2个零配件供应环节增加一个供应商，转入下一步继续搜索，直到R≥0.96为止。搜索过程中各零配件供应商数量的变化和可靠度如表2所示，经过8次搜索后得到最优解。最终的结果如表3所示。

表2 最优供应商数量搜索过程Table 2 Search process for the number of the optimal suppliers

若在搜索算法中仅以式(5)中的可靠性重要度为依据进行搜索，则得到的最优解如表4所示。

对比表3、表4可以看出，虽然两种方法得出的最优解均可满足供应链可靠性要求，但同时考虑可靠度与成本的综合重要度系数搜索算法得出的供应链总成本明显更低，因此供应商数量的设置更为合理。

表3 可靠性优化设计的最优解Table 3 Optimal solution of reliability optimization design

表4 仅考虑可靠性重要度时的最优解Table 4 The optimal solution only considering reliability importance

4 结论

本文针对制造商(核心企业)与供应商构成的两级供应链在规划设计时的可靠性优化设计问题，提出了供应链最优化模型。该模型充分考虑了供应链各个环节供应商的不确定性和市场价格的不确定性，更加贴近实际情况。在模型的求解中，提出了同时考虑供应链可靠性和成本的综合重要度系数及搜索算法。实例分析表明，本文提出的方法能够在满足可靠性要求的前提下有效确定供应链中各个环节供应商的最优数量，从而使供应链总成本最低。该方法可为核心企业在供应链设计阶段优化供应商数量提供理论依据。另外，虽然本文研究的对象是制造商-供应商组成的两级供应链，但对于多级供应链的可靠性优化设计，本文提出的方法同样适用。