一维六方准晶双材料中圆孔边共线界面裂纹的反平面问题*

张炳彩， 丁生虎， 张来萍

（1. 宁夏大学新华学院，银川 750021；2. 宁夏大学 数学统计学院，银川 750021）

引 言

准晶自1982 年被Shechtman 等[1]发现以来，引起了众多科研人员的关注.准晶材料具有高硬度、不粘性、耐腐蚀等诸多优良特性，在很多方面具有重要的应用价值.由于准晶材料的脆性特性[2]，在生产过程中难免会产生一些缺陷(裂纹、夹杂和位错等)，在外应力的作用下，很容易发生断裂.尤其对于含有孔洞的准晶材料，孔洞周围形成的应力集中区易产生裂纹，而裂纹的扩展又导致材料结构的损伤，从而导致材料的断裂破坏.因此，研究准晶材料的断裂问题具有重要的理论和实际意义.

目前，已有众多学者对准晶材料的断裂问题进行了研究[3-6].在工程实际中，开孔结构是一种较为常见的结构.郭俊宏和刘官厅[7]研究了一维六方准晶圆形孔边裂纹问题.之后，郭俊宏等[8-10]又研究了一维六方准晶椭圆孔边裂纹问题，运用复变函数方法给出了问题的解析解.Li 和Liu[11]研究了二十面体准晶中位错与椭圆孔的相互作用问题，利用扩展的Stroh 公式、保角变换方法和摄动技术得到了该问题的封闭解.利用复变函数方法和保角映射方法，Yang 等[12]研究了一维六方压电准晶材料中带不对称三裂纹的圆形孔口的断裂问题.白巧梅和丁生虎[13]研究了一维六方压电准晶中正六边形孔边裂纹的反平面问题，利用复变函数方法，得到了孔边裂纹尖端的应力分布以及场强度因子的解析解.利用推广的连续位错层法，Tupholme[14-15]研究了一维六方准晶中运动的反平面剪切裂纹.

以上文献主要针对准晶单一材料的断裂问题开展研究，而在实际工程中常见由两种不同（或相同）材料拼接而成的组合材料，在外部应力作用下界面处很容易产生缺陷.El-Borgi 等[16]用奇异积分方程和有限元方法分析研究了在热载荷和机械载荷作用下功能梯度涂层与均匀基体之间的界面裂纹.Kuang 和Wang[17]用边界配置法研究了双材料板中孔产生的界面裂纹问题.Loboda 等[18]分析了由两个半无限大一维压电准晶材料结合在一起的双材料中的电渗透裂纹的平面问题，提出了电渗透界面裂纹的一种精确解析解.基于复变函数和保角映射方法，Song 和Hassan[19]计算了含径向对称裂纹的横观各向同性压电双材料在非圆形空腔边缘附近的动态应力强度因子.An 等[20]利用Green 函数法和坐标变换法求解了偏心圆孔附近具有可渗透界面裂纹的压电双材料动态反平面剪切问题.An 和Song[21]研究了功能梯度压电双材料中圆孔附近可渗透界面裂纹尖端的应力集中问题.

对于准晶双材料裂纹问题，Zhang 等[22]利用Stroh 公式研究了由两个不同准晶半平面组成的无限平面问题，得到了一维准晶双材料内部和界面Green 函数的解.Hu 等[23-24]利用积分方程和复变函数方法，研究了具有压电效应的，不同一维六方准晶材料受反平面剪切应力和面内电应力作用下的界面裂纹问题.Fan 等[25]利用Stroh 公式得到了一维六方准晶双材料界面上声子场和相位子场位错和开口位移的Green 函数.Zhao 等[26]提出用位移不连续法分析一维六方准晶涂层在面内应力作用下的界面裂纹问题.然而，关于准晶双材料孔边界面裂纹问题的研究尚未见有文献报道.

事实上，随着复合材料和新型材料的发展，工程中经常出现带裂纹的孔口问题，而复变函数解法是求解复杂孔口问题最优越的方法.由于准晶材料声子场和相位子场的耦合性，及孔洞形状的复杂性，研究准晶材料双材料孔边裂纹问题具有一定的挑战.因此，本文应用复变函数方法，分析研究了一维六方准晶双材料圆孔边不对称共线界面裂纹的反平面问题，所得的结果对工程结构裂纹止裂具有理论意义和实用价值.

1 基 本 公 式

本文研究了一维六方准晶反平面问题.取x3轴为一维六方准晶体的准周期方向，x1Ox2坐标面为其周期平面.根据准晶弹性理论[27]，当一维六方准晶体中含有的圆孔洞及孔边裂纹沿准周期方向穿透时，变形不随变量x3变化，只与变量x1和x2有关.此时，平衡方程(不考虑体力)为

几何方程为

广义Hooke 定律为

确定所有场变量，其中上标T 表示矩阵的转置.

2 问题描述及求解

2.1 问题描述

如图1 所示，考虑两种不同的一维六方准晶双材料拼接在一起，x3轴正方向为一维六方准晶体的准周期方向，x1Ox2坐标面为其周期平面，x1Ox3平面为拼接界面.在拼接界面处存在一圆孔洞，且圆孔两边在x1轴上分别有一直线裂纹.假设准晶双材料在无穷远场受沿声子场和相位子场边界的反平面剪切应力作用σ32=τ0,H32=H0，圆孔及裂纹面为自由面.

图1 含圆孔孔边界面裂纹的一维六方准晶双材料Fig. 1 One dimensional hexagonal quasicrystal bi-materials with interface cracks emanating from a circular hole

根据准晶线弹性理论[27]，仅对应力集中而言，可将该问题转化为圆孔及裂纹表面受剪切应力作用的问题.此时边界条件可表示为

该变换将圆孔保角变换到直线裂纹.

利用该保角变换，将z平面内的x1轴变换为ς平面内的ξ轴，圆孔及孔边裂纹都变换为直线裂纹，且将点z=±Ri变换为ς=0，z=±R变换为ς=±1，左右裂尖z=−R−L2，z=R+L1分别变换为点：

对应关系如图2 所示.

图2 保角变换示意图Fig. 2 The diagram of conformal mapping

ς平面内直线裂纹长2L=ς2−ς1，由于坐标原点ς=0不一定是直线裂纹中心，可通过平移将直线裂纹中心移到原点.因此通过式(9)将z平面内圆孔孔边裂纹问题转化为ς平面内的直线裂纹问题.

考虑保角变换的性质， ς平面内边界条件可表示为

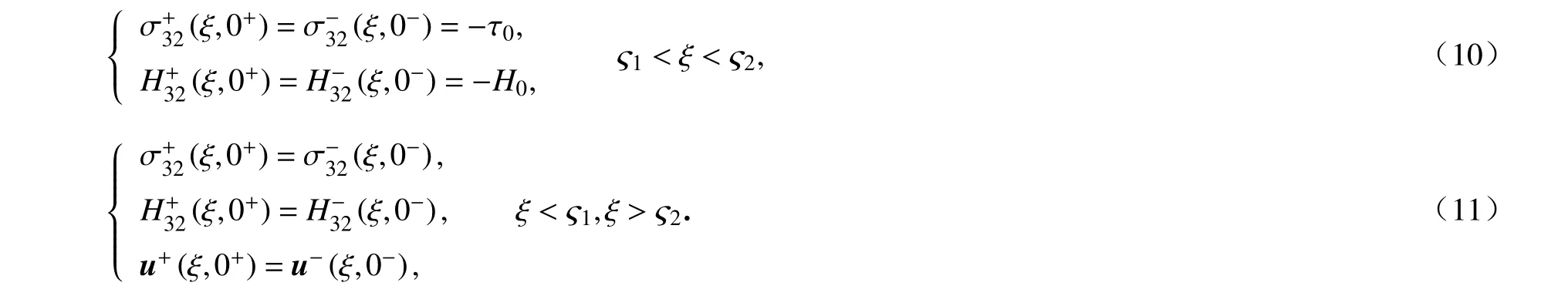
式(4)两边关于x1求导，可得

2.2 应力强度因子及能量释放率

3 数 值 算 例

下面通过数值算例分析几何尺寸对等效应力强度因子的影响和耦合系数、声子场应力和相位子场应力对能量释放率的影响.

3.1 几何尺寸对应力强度因子的影响

为了讨论圆孔半径和裂纹长度对声子场、相位子场等效应力强度因子的影响，本文取不同的圆孔半径和裂纹长度，绘出式(29)的图形，观察等效应力强度因子的变化情形.

图3 给出在不同圆孔半径下，等效应力强度因子K随右裂纹长度L1/R的变化关系(L2/R=0.02).可以发现，当半径给定时，等效应力强度因子K随右裂纹长度的变化呈快速增长趋势.但在裂纹长度一定的情况下，随着圆孔半径的增大，K有减小的趋势.

图4 给出不同左裂纹长度情况下，等效应力强度因子K随右裂纹长度L1/R的变化关系(R=0.1 m).在圆孔半径和左裂纹长度一定的情况下，等效应力强度因子K随右裂纹长度增加先减小后增加，最后趋向稳定值.而当圆孔半径一定时，等效应力强度因子K随左裂纹的长度增大而缓慢增加，该结果和文献[29]不考虑电场时圆孔边不对称裂纹所得结果一致.图3 和图4 的结果说明圆孔半径和裂纹长度的变化都对裂纹尖端应力场有一定的影响.

图4 不同L2/R, K 随L1/R的变化情形Fig. 4 For different L2/R values, the change of K with L1/R

3.2 耦合系数、声子场应力和相位子场应力对能量释放率的影响

本小节算例考虑两种情形： ① 在上下两种准晶材料其他参数不变的情况下，讨论声子场和相位子场耦合系数对能量释放率的影响(图5、6); ② 上下准晶材料参数不同时，讨论声子场应力和相位子场应力对能量释放率的影响(图7).两种不同一维六方准晶材料的材料参数如表1 所示.

表1 两种不同一维六方准晶材料的参数取值[25,30]Table 1 Parameter values of 2 different 1D hexagonal quasicrystals[25,30]

图5、6 分别给出了在不同耦合系数下，能量释放率G随相位子场应力H0(τ0=6 MPa,R=0.3 m,L1/R=0.3,L2/R=0.2)和右裂纹长度L1/R的变化关系(τ0=6 MPa,H0=4 MPa,R=0.3 m,L2/R=0.2).由图5、6 可知，当材料耦合系数增大时, 能量释放率G也在增大；当耦合系数不变时，能量释放率G随着相位子场应力H0和右裂纹长度L1/R的增大而增大；当上下材料参数相同(单材料)时，固定耦合系数，能量释放率随相位子场应力H0或右裂纹长度L1/R的增大也在增大，该结果和文献[29]不考虑电场时圆孔边不对称裂纹所得结果一致.从以上结果可以发现，准晶双材料耦合系数的变化比单材料耦合系数的变化对能量释放率的影响更大，更容易促进裂纹的扩展.

图5 不同的R3, G 随H0 的变化情形Fig. 5 For different R3 values, the change of G with H0

图6 不同的R3, G 随L1/R 的变化情形Fig. 6 For different R3 values, the change of G with L1/R

图7 给出了声子场应力和相位子场应力对能量释放率的影响(R=0.1 m,L1=0.01 m,L2=0.03 m).由图7可知，能量释放率随着声子场应力的增大而增大，随相位子场应力从负值变到正值时，先减小再增大，当相位子场应力取某个特定值时，又可使能量释放率达到最小.这说明一维六方准晶材料声子场应力和相位子场应力对能量释放率都有一定的影响，能促使裂纹的扩展.但当相位子场应力取一定值时，又可以抑制裂纹的扩展.

4 结 论

本文研究了一维六方准晶双材料中圆孔边不对称共线界面裂纹的反平面问题.首先根据保角变换将圆孔边不对称共线裂纹问题转化为直线裂纹问题；其次在准晶体受远场声子场应力和相位子场应力作用，圆孔和裂纹面自由的边界条件下，利用Stroh 公式和复变函数方法推导出新平面内裂纹尖端应力强度因子和能量释放率的解析表达式.通过数值算例分析了几何尺寸对等效应力强度因子的影响，以及耦合系数、声子场应力和相位子场应力对能量释放率的影响，得到了以下结论：

1) 应力强度因子随圆孔半径的增大而减小；

2) 圆孔半径和左裂纹长度一定时，等效应力强度因子K随右裂纹长度增加先减小后增加，最后趋向稳定值；

3) 能量释放率随耦合系数的增大而增大，当耦合系数不变时，能量释放率也随着相位子场应力和右裂纹长度的增大而增大；

4) 远场声子场应力和相位子场应力对能量释放率都有一定的影响，但当相位子场应力取一定值时，能量释放率达到最小，可以抑制裂纹的扩展.

参考文献（ References ） ：

［1］S HECHTMAN D, BLECH I, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J].Physical Review Letters, 1984, 53（20）: 1951-1954.

［2］孟 祥敏, 佟百运, 吴玉琨. Al65Cu20Co15准晶体的力学性能[J]. 金属学报, 1994, 30（2）: 61-64. （MENG Xiangmin,TONG Baiyun, WU Yukun. Mechanical properties of Al65Cu20Co15quasicrystal[J].Acta Metallurgica Sinica,1994, 30（2）: 61-64.（in Chinese））

［3］F AN T Y, LI X F, SUN Y F. A moving screw dislocation in a one-dimensional hexagonal quasicrystal[J].Acta Physica Sinica(Overseas Edition), 1999, 8（4）: 288-295.

［4］L I L F, FAN T Y. Exact solutions of two semi-infinite collinear cracks in a strip of one dimensional hexagonal quasicrystal[J].Applied Mathematics and Computation, 2008, 196（1）: 1-5.

［5］W ANG X, PAN E. Analytical solutions for some defect problems in 1D hexagonal and 2D octagonal quasicrystals[J].Pramana, 2008, 70（5）: 911-933.

［6］Z HOU J M, LI L H, Wang G X. Dynamic problems in a decagonal quasicrystal with a mode Ⅱ Griffith crack[J].Chinese Journal of Engineering Mathematics, 2021, 38（1）: 136-150.

［7］郭 俊宏, 刘官厅. 一维六方准晶中具有不对称裂纹的圆形孔口问题的解析解[J]. 应用数学学报, 2007, 30（6）: 1066-1075. （GUO Junhong, LIU Guanting. Analytic solutions of the one-dimensional hexagonal quasicrystals about problem of a circular hole with asymmetry cracks[J].Acta Mathematicae Applicatae Sinica, 2007, 30（6）: 1066-1075.（in Chinese））

［8］郭 俊宏, 刘官厅. 一维六方准晶中带双裂纹的椭圆孔口问题的解析解[J]. 应用数学和力学, 2008, 29（4）: 439-446.（GUO Junhong, LIUGuanting. Analytic solutions of problem about an elliptic hole with two straight cracks in one-dimensional hexagonal quasicrystals[J].Applied Mathematics and Mechanics, 2008, 29（4）: 439-446.（in Chinese））

［9］G UO J H, LIU G T. Exact analytic solutions for an elliptic hole with asymmetric collinear cracks in a one-dimensional hexagonal quasi-crystal[J].Chinese Physics B, 2008, 17（7）: 2610-2620.

［10］G UO J H, LU Z X. Exact solution of four cracks originating from an elliptical hole in one-dimensional hexagonal quasicrystals[J].Applied Mathematics and Computation, 2011, 217（22）: 9397-9403.

［11］L I L H, LIU G T. Interaction of a dislocation with an elliptical hole in icosahedral quasicrystals[J].Philosophical Magazine Letters, 2013, 93（3）: 142-151.

［12］Y ANG J, LI X, DING S H. Anti-plane analysis of a circular hole with three unequal cracks in one-dimensional hexagonal piezoelectric quasicrystals[J].Chinese Journal of Engineering Mathematics, 2016, 33（2）: 184-198.

［13］白 巧梅, 丁生虎. 一维六方压电准晶中正六边形孔边裂纹的反平面问题[J]. 应用数学和力学, 2019, 40（10）: 1071-1080. （BAI Qiaomei, DING Shenghu. An anti-plane problem of cracks at edges of regular hexagonal holes in 1D hexagonal piezoelectric quasicrystals[J].Applied Mathematics and Mechanics, 2019, 40（10） : 1071-1080.（ in Chinese））

［14］T UPHOLME G E. An antiplane shear crack moving in one-dimensional hexagonal quasicrystals[J].International Journal of Solids and Structures, 2015, 71: 255-261.

［15］T UPHOLME G E. Row of shear cracks moving in one-dimensional hexagonal quasicrystal line materials[J].Engineering Fracture Mechanics, 2015, 134: 451-458.

［16］E L-BORGI S, ERDOGAN F, HATIRA F B. An interface crack between a functionally graded coating and a homogeneous substrate under thermo-mechanical loading[J].Materials Science Forum, 2003, 423/425: 601-606.

［17］K UANG J S, WANG Y H. Analysis of interfacial cracks emanating from a hole in a bi-material plate[J].European Journal of Mechanics A:Solids, 1999, 18（3）: 465-479.

［18］L OBODA V, KOMAROV O, BILYI D, et al. An analytical approach to the analysis of an electrically permeable interface crack in a 1D piezoelectric quasicrystal[J].Acta Mechanica, 2020, 231（8）: 3419-3433.

［19］S ONG T S, HASSAN A. Dynamic anti-plane analysis for symmetrically radial cracks near a non-circular cavity in piezoelectric bi-materials[J].Acta Mechanica, 2015, 226（7）: 2089-2101.

［20］A N N, SONG T S, HOU G L. Interfacial cracks near an eccentric circular hole in piezoelectric bi-materials subjected to dynamic incident anti-plane shearing[J].AIP Advances, 2020, 10（5）: 1-11.

［21］A N N, SONG T S. Dynamic fracture behavior for functionally graded piezoelectric bi-materials with interfacial cracks near a circular hole[J].Waves in Random and Complex Media, 2021: 1-19. DOI: 10.1080/17455030.2021.1936284.

［22］Z HANG L L, WU D, XU W S, et al. Green’s functions of one-dimensional quasicrystal bi-material with piezoelectric effect[J].Physics Letters A, 2016, 380（39）: 3222-3228.

［23］H U K Q, GAO C F, ZHENG Z, et al. Interaction of collinear interface cracks between dissimilar one-dimensional hexagonal piezoelectric quasicrystals[J].ZAMM:Zeitschrift fur Angewandte Mathematic und Mechanik, 2021,101（11）: 1-26.

［24］H U K Q, JIN H, YANG Z J, et al. Interface crack between dissimilar one-dimensional hexagonal quasicrystals with piezoelectric effect[J].Acta Mechanica, 2019, 230（7）: 2455-2474.

［25］F AN C Y, CHEN S, ZHANG Q Y, et al. Fundamental solutions and analysis of an interfacial crack in a one-dimensional hexagonal quasicrystal bi-material[J].Mathematics and Mechanics of Solids, 2020, 25（5）: 1124-1139.

［26］Z HAO M H, FAN C Y, LU C S, et al. Analysis of interface cracks in one-dimensional hexagonal quasi-crystal coating under in-plane loads[J].Engineering Fracture Mechanics, 2021, 243: 107534.

［27］F AN T Y.Mathematical Theory of Elasticity of Quasicrystals and Its Application[M]. Beijing: Science Press,2010.

［28］M USKHELISHVILI N I.Some Basic Problems of the Mathematical Theory of Elasticity[M]. Groningen, Holland:Noordhoff, 1953.

［29］杨 娟. 压电效应下一维六方准晶中孔边多裂纹反平面断裂问题研究[D]. 博士学位论文. 银川: 宁夏大学, 2015.（YANG Juan. Study on anti-plane fracture problems of Multiple cracks emanating from a hole in one-dimensional hexagonal quasicrystals with piezoelectric effects[D]. PhD Thesis. Yinchuan: Ningxia University, 2015. （in Chinese））

［30］Z HOU Y B, LI X F. Exact solution of two collinear cracks normal to the boundaries of a 1D layered hexagonal piezoelectric quasicrystal[J].Philosophical Magazine, 2018, 98（19）: 1780-1798.