散体介质SHPB 被动围压试验体应力计算的理论修正方法*
2022-07-11陈昊祥邓树新王德荣王明洋
陈昊祥,李 杰,邓树新,王德荣,王明洋,
(1. 北京建筑大学土木与交通工程学院, 北京 100044;2. 陆军工程大学爆炸冲击防灾减灾国家重点实验室, 江苏 南京 210007;3. 南京理工大学机械工程学院, 江苏 南京 210094)
散体介质作为消波耗能材料广泛地应用于土木工程以及军事工程等领域,其在高应变率下的动态物理力学性质对于研究爆炸冲击荷载作用下结构的防灾减灾问题具有重要意义。然而,关于中高应变率(10~10s)下散体材料是否具有应变率效应,现有研究尚存在严重分歧。Yamamuro 等发现干砂的应力-应变曲线在不同应变率(10~10s)下存在明显差别,具有显著的应变率效应。Luo 等的试验结果却显示,不同应变率下散体材料的应力-应变曲线基本相同,未发现明显的应变率效应。造成上述差异的原因可能在于,约束条件选取的不同,具体原因尚有待进一步研究。而且,随着我国南部海域岛礁建设的蓬勃发展,散体介质中-高应变率下的动态力学性质研究的应用前景越来越广阔。
分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)是研究材料中-高应变率下动态力学性质的重要试验手段。相较于固体材料,散体介质SHPB 试验过程中需要使用刚性套筒固定散体材料试样。通过测量套筒外壁的环向应变,根据厚壁圆筒理论(平面应力状态)即可反推出散体介质试样中的应力与变形场。需要指出的是,散体材料的波阻抗较低,为了保证整个试验过程中试样内部的应力平衡,试样的长度通常较短(一般不超过10 mm)。由于套筒的约束使得散体介质试样边缘处产生了显著的端部效应(如图1 所示),此时套筒不能满足平面应力假设,因此文献[2-3, 9]中得到的结果并不准确,需要进行修正。魏久淇等指出上述文献中计算存在的缺陷,尝试通过数值模拟手段进行修正并与试验结果对比,验证了数值修正方法的正确性,但受限于数值模拟方法自身的缺陷,他们未能给出修正系数的无量纲形式,导致数值修正方法的适用范围有限。
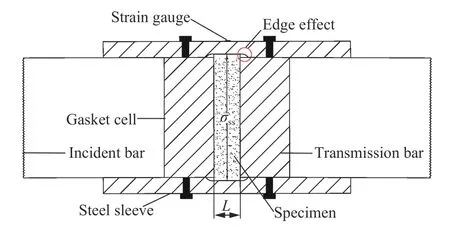
图1 钢套筒端部效应的示意图Fig. 1 The configuration for the edge effect in the steel sleeve
受魏久淇等研究的启发,本文中借助经典板壳理论,将刚性套筒简化为受均匀带状内压作用的圆柱形壳体,推导套筒径向位移、环向应变与带状内压及套筒几何、力学参数的关系,得到套筒径向位移、环向应变沿其轴向的分布;分析套筒长度、厚度、内外径以及带状内压宽度之间等无量纲几何参数对计算结果的影响;将理论计算结果与试验结果和数值模拟结果进行对比,验证理论计算的正确性。
1 厚壁圆筒理论计算试样中的应力场
为了探究聚合物材料在大变形条件下的非弹性力学行为,Ma 等采用厚壁圆筒理论对试样中的应力场进行了估算,后续的散体介质SHPB 被动围压试验研究大多采用了相同的计算方法。
假设散体试样与套筒之间的径向应力满足连续性条件,在极坐标下,试样内部的应力和变形分别为:
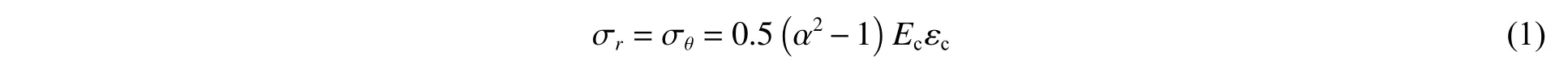
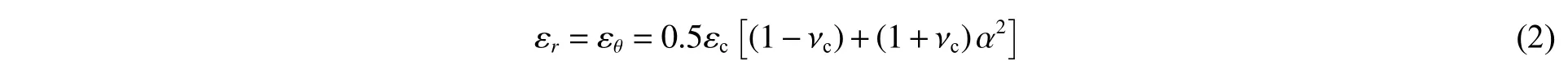

由式(1)~(2)可知,试样的静水压力 σ 和体积应变ε分别为:
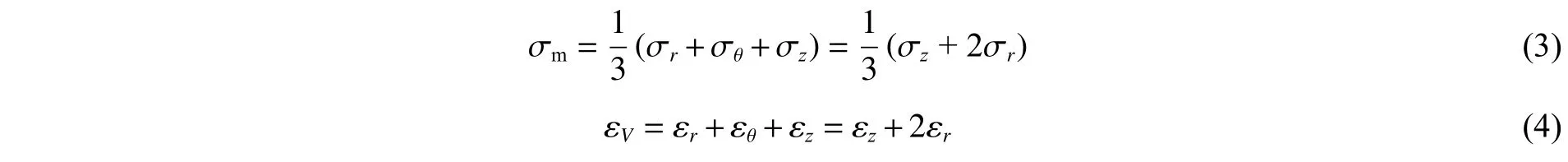
考虑到试样轴向应变 远εε大于径r向 和环ε向应变θ , 即ε≫ε=ε,于是试样的体积应变可化简为:
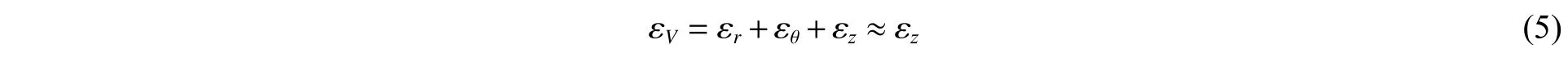
通过测量套筒外壁环向应变 ε,并结合式(1)~(5),即可得到散体介质试样的应力与变形状态。需要注意的是,上述理论推导过程中假定套筒处于平面应力状态,但由于端部效应的存在,套筒受力并不能简化为平面应力问题,因此计算需要修正。
2 圆柱壳体理论计算试样中的应力场
为了便于环向应变 ε的量测以及试件装样,在进行散体介质SHPB 试验时通常选用壁厚较薄的刚性套筒。试验过程中试样内部始终处于应力平衡状态,因此可将试样与套筒间的相互作用力按静力处理。此时,套筒可简化为受均匀带状内压作用的圆柱形壳体,如图2 所示。图2中,套筒长度为2,均匀内压强度()作用长度为2,取极坐标(,,)。
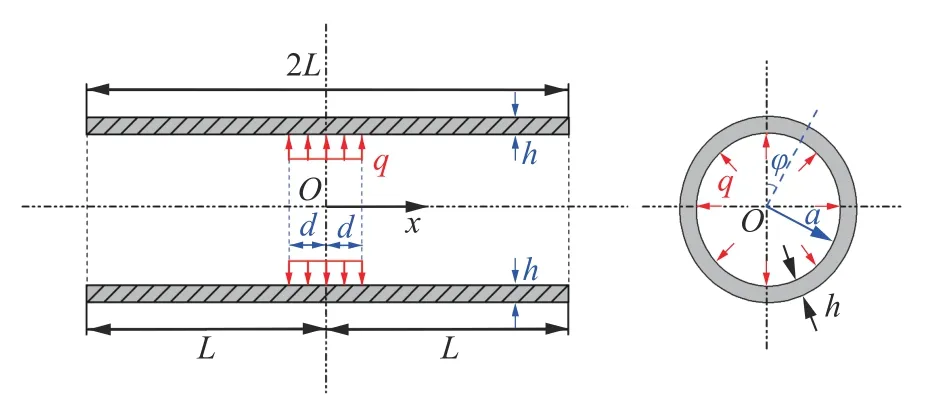
图2 套筒受力Fig. 2 Stress on the steel sleeve
由经典弹性板壳理论可知,忽略轴向变形,均匀内压作用下套筒的平衡方程为:

对均匀内压()进行Fourier 级数展开,可得:
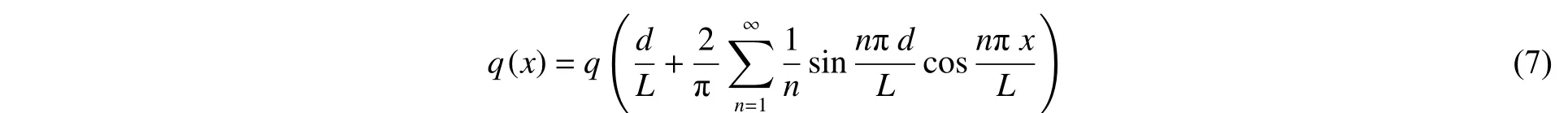
将式(6)对坐标进行Fourier 变换并化简,可得:
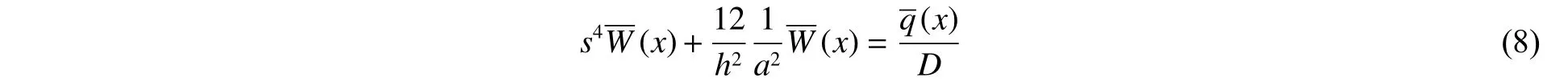
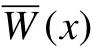
对式(8)进行Fourier 逆变化,可得套筒径向位移函数():
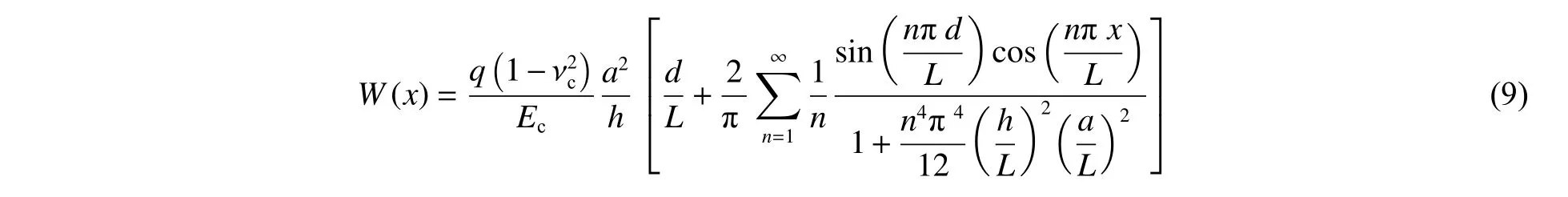

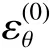
3 数值模拟与理论对比
为了验证本文计算模型的正确性,采用文献[4]中试验参数并与其数值模拟结果进行对比,数值模拟过程中参数选取为:套筒长度2=94 mm,套筒厚度=4.95 mm,套筒内半径=18.55 mm,套筒外半径=23.5 mm,套筒弹性模量=210 GPa,泊松比ν=0.3;带状内压宽度2=7, 8, 9, 10, 12, 15, 20, 30, 40, 50,60, 70, 80, 90, 94 mm。
将上述计算参数代入式(10),可求得环向应变沿套筒长度方向的分布曲线,如图3 所示。由图3 发现,随着内压宽度的增大,环向应变的分布范围扩大、幅值先增大后减小。当带状内压宽度2=10 mm(散体介质试样的长度极限)时,环向应变的分布范围约为套筒长度的1/3,此时柱壳理论计算结果约为厚壁圆筒理论结果的0.5 倍,表明厚壁圆筒理论计算结果与实际变形相差较大;当2≈40 mm 时,柱壳理论计算结果达到最大值,约为厚壁圆筒理论结果的1.06 倍;当2=2时,柱壳退化为厚壁圆筒。
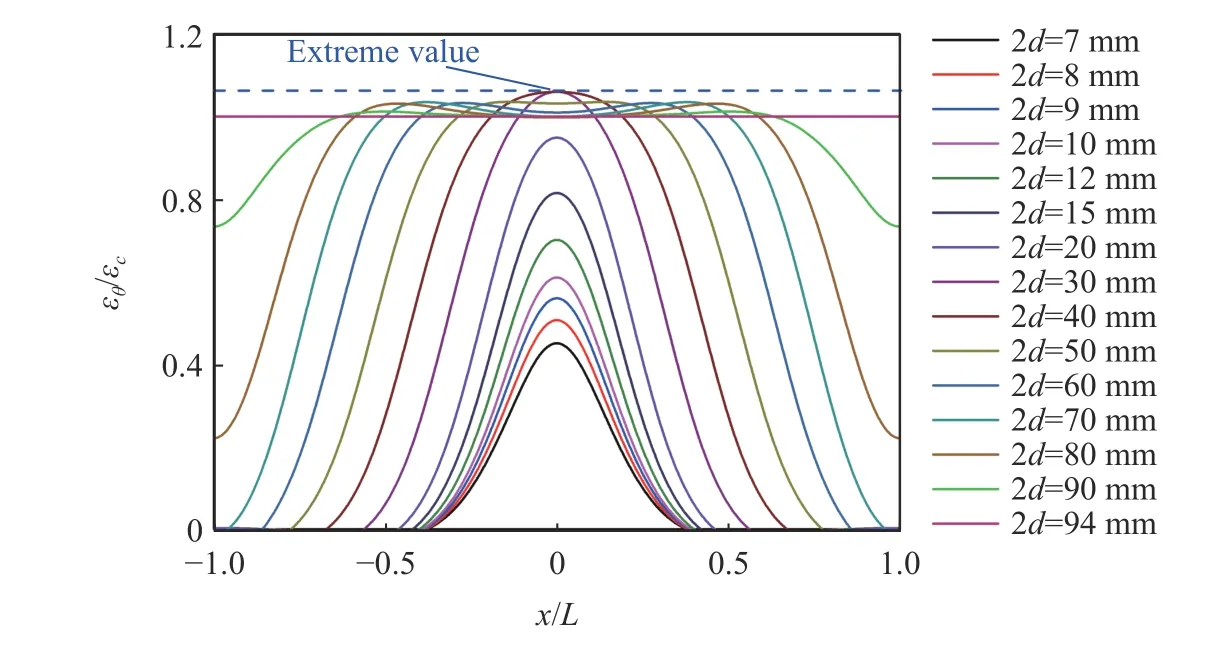
图3 套筒环向应变沿轴线的分布Fig. 3 Distribution of hoop strain on the outer surface along with the steel sleeve
将文献[4]中数值计算得到的修正系数与圆柱壳体理论计算结果进行对比,如图4 所示。由图4可知,当/≤0.25 时,壳体理论计算结果与数值计算结果基本重合,而与厚壁圆筒理论计算结果则相差较远;当0.25</≤0.625 时,壳体理论计算结果略高于数值和厚壁圆筒理论计算结果,最大误差为6%;当/>0.625 时,理论计算结果和数值计算结果基本相同,此时2 种理论精度都可满足试验要求。
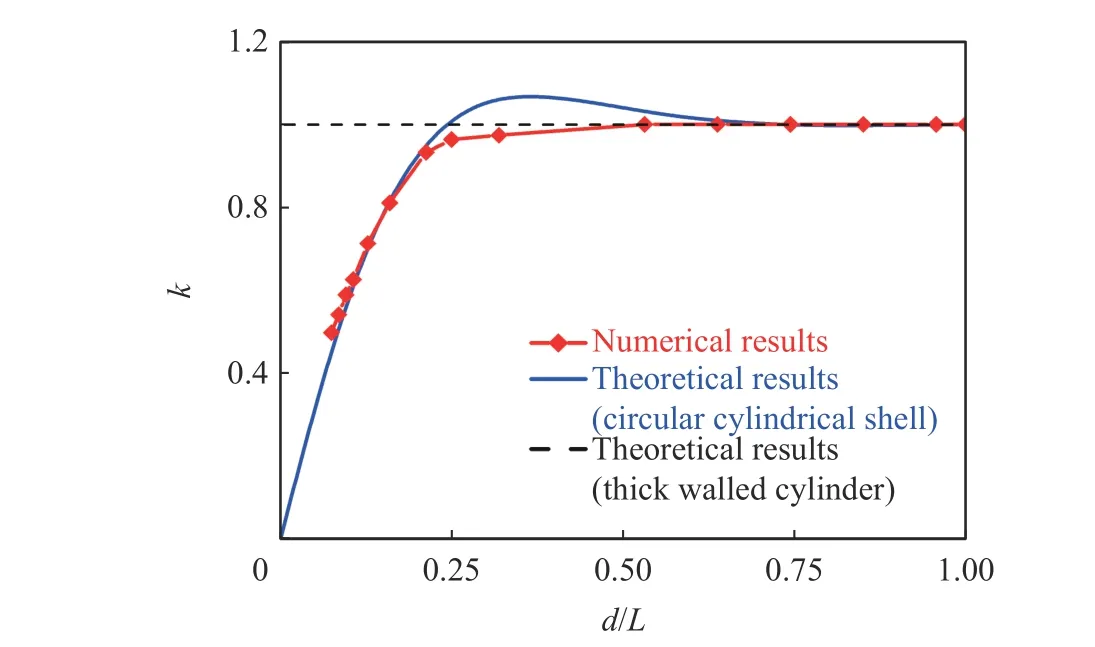
图4 理论计算得到的修正系数与数值模拟结果的比较Fig. 4 Comparison of theoretical correction factors with numerical results
为了进一步验证壳体理论计算结果的准确性,并分析套筒长度、内外径以及均匀带状内压宽度等几何参数对计算结果的影响,本文中在文献[4]中数值计算的基础上,利用Abaqus/Explicit 有限元模拟软件进行补充计算,模型网格采用六面体线性缩减积分单元,边界条件为自由边界,不同计算模型网格划分示意图如图5 所示。

图5 模型网格划分Fig. 5 The element meshes for the numerical models
算例1:套筒长度2=94 mm,套筒厚度=3 mm,套筒内半径=19 mm,套筒外半径=22 mm,套筒弹性模量=210 GPa,泊松比ν=0.3;带状内压宽度2=7, 8, 9, 10, 12, 15, 20, 30, 40, 50, 60, 70, 80, 90,94 mm。此时,理论计算与数值计算对比结果如图6 所示。
算例2:套筒长度2=50 mm,套筒厚度=4.95 mm,套筒内半径=18.55 mm,套筒外半径=23.5 mm,套筒弹性模量=210 GPa,泊松比ν=0.3;带状内压宽度2=7, 8, 9, 10, 12, 15, 20, 30, 40, 50 mm。此时,理论计算与数值计算对比结果如图7 所示。
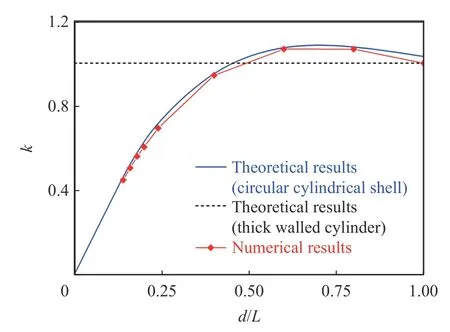
图7 理论计算得到的修正系数与数值模拟结果的比较(算例2)Fig. 7 Comparison of theoretical correction factors with numerical results (case 2)
对比图6~7 中理论与数值计算结果可以发现,随着无量纲参数/、/、/的改变,壳体理论的计算结果与数值计算结果非常接近,且精度远高于厚壁圆筒理论。
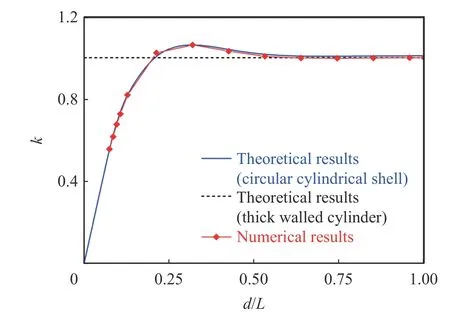
图6 理论计算得到的修正系数与数值模拟结果的比较(算例1)Fig. 6 Comparison of theoretical correction factors with numerical results (case 1)
4 试验与理论对比
为了进一步验证壳体理论的准确性,将理论计算与试验结果进行对比,试验结果同样采用文献[4]中的数据,具体如图8 所示。根据试验数据计算可知,含水质量分数ω 为25%和30%的钙质砂试样SHPB 试验对应的饱和点(饱和度S= 1)分别为ε=0.221 2 和ε=0.157 4。当轴向应变ε超越饱和点之后,水压力将占据主导地位,此时散体试样处于静水压力状态,即σ=σ=σ。
观察图8 可以发现,当轴向应变在饱和点之前,理论计算的径向应力σ明显小于轴向应力σ试验值,这是由散体介质的侧向压力系数λ 通常小于1 引起的。根据试验和理论数据进行估算,可知λ≈0.548;当轴向应变超过饱和点之后,壳体理论(式(10))计算得到的径向应力σ与轴向应力σ的试验值基本重合,验证了壳体理论的准确性。而厚壁圆筒理论(式(1))的计算结果则明显低于试验值,表明厚壁圆筒理论的计算误差很大,此时并不适用。
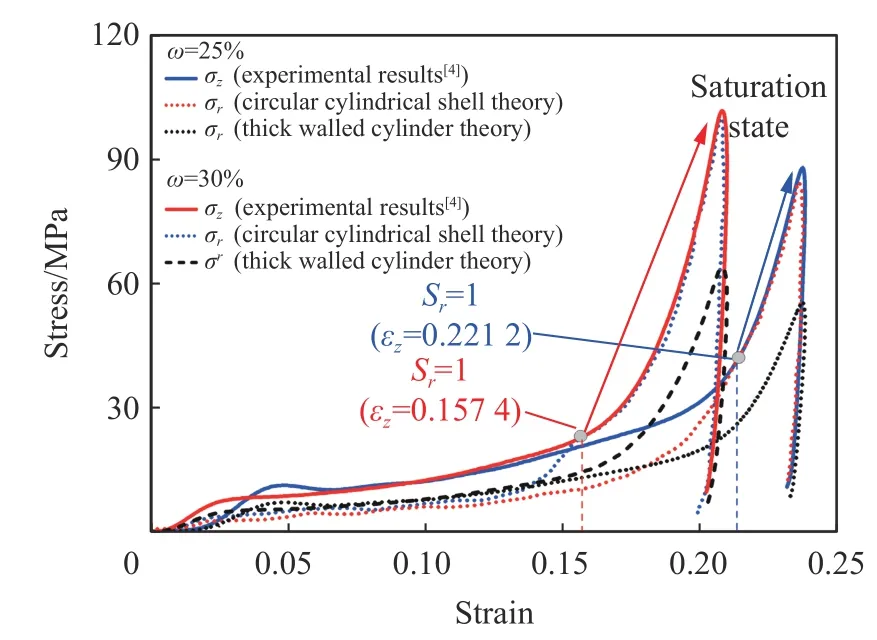
图8 理论轴向应力-应变理论曲线与试验结果[4]的比较Fig. 8 Comparison of theoretical axial stress-stain curves with experimental results[4]
5 结 束 语
SHPB 被动围压试验为探究散体介质在爆炸和冲击荷载作用下的力学行为提供了一个行之有效的方法。本文中针对相关试验设计和计算中存在的弊端和不足,借助经典板壳理论对现有计算方法进行修正,总结如下。
(1)将SHPB 被动围压试验中用于约束散体介质的刚性套筒简化为受均匀带状内压作用的圆柱形壳体。推导了套筒径向位移、环向应变与均匀带状内压及套筒几何、力学参数的定量关系,得到了套筒径向位移、环向应变沿其轴向的分布。
(2)分析了套筒长度、厚度、内外径以及均匀带状内压宽度之间等无量纲几何参数对计算结果的影响,并与数值计算结果进行对比,验证了修正系数的准确性。
(3)将理论结果与试验和数值模拟结果进行对比分析,验证了理论计算的正确性。
