冲击载荷下轻质夹芯拱最大刚度拓扑优化及动力响应*

刘 颢，白 震，李志强，李世强

（1. 太原理工大学机械与运载工程学院应用力学研究所，山西 太原 030024；2. 太原理工大学材料强度与结构冲击山西省重点实验室，山西 太原 030024；3. 山西省检验监测中心（山西省标准计量技术研究院），山西 太原 030024）

多孔夹芯结构作为一种具有高比刚度/比强度、轻质、抗冲击、吸能等功能特性的多功能一体化结构，在航空航天、交通运输、工程结构等领域都有着很好的应用前景。高孔隙率的多孔金属（泡沫、蜂窝、波纹板、 点阵结构等）由于其具有良好的声、热、电磁屏蔽等功能，优异的比强度/比刚度，良好的吸能缓冲特性，丰富多变的胞孔细观构型，作为夹芯结构芯层，可满足各种服役环境下的材料和结构一体化多功能协同设计需求。有关这类结构在冲击载荷作用下动力响应的研究大部分集中在性能探索、应用开发和参数优化设计方面，对于设计空间更大的结构拓扑设计，还缺乏深入的研究。究其原因：首先，材料细观拓扑构型对宏观结构的影响机理复杂，缺乏针对性、专门性的设计目标；其次，优化过程中需要综合考虑载荷历程和结构弹塑性响应对结构设计变量的影响，涉及载荷的时空非线性和材料/结构的惯性效应、应变率效应，导致目标函数复杂，敏度分析困难；最后，制备具有专门设计且拓扑构型复杂的多孔材料难度较大。随着结构拓扑优化技术和3D 打印技术的日渐成熟，冲击载荷下结构的拓扑优化设计与性能测试、评估受到越来越多学者的关注。

拓扑优化的主要思想是在给定的约束条件下，通过改变结构和材料的构型和分布，来实现结构和材料性能的提高。常用到的拓扑优化方法有变密度法、均匀化法和渐进结构优化法（evolutionary structural optimization, ESO）。Querin 等对渐进结构法进行了改进与延伸，提出了双向渐进结构优化法（bi-directional evolutionary structural optimization，BESO），在优化过程中可以增添和删除单元。之后，Huang 等针对结构刚度优化，提出了一种基于灵敏度分析的改进BESO 法，该方法解决很多拓扑优化中常见的问题，如棋盘格、优化收敛性等。

目前，拓扑优化大多集中在静态载荷优化，而工程应用中常见的是动态载荷。针对动载优化中出现的收敛困难、计算时间长等问题，Choi 等和Park 等提出了等效静态载荷法（equivalent static loads optimization, ESLO），建立双层拓扑优化流程，在外层中对动态载荷工况下的结构响应进行分析，并将动态载荷等效为具有相同位移响应的静态载荷，在内层中对等效静态载荷下的结构进行拓扑优化。蓝萌等针对等效静态载荷法计算效率低、优化流程复杂的问题，将双向渐进结构优化法作为优化方法，对动态载荷优化流程进行了改进，提高了优化效率。王宪杰等引入基于惩罚指数的材料插值方案，对传统BESO 法进行了数值计算方面的改进，并分别对宏观结构、微观结构、材料/结构一体化等问题进行了多尺度、多相复合材料布局以及拓扑优化。闫琨和Yan 等结合各类算法的优点，在线弹性范围内，提出了一种考虑初始载荷激励和时间效应对结构设计变量影响的灵敏度分析计算方法，利用该方法研究了残余振动最小化结构优化设计问题和结构耐撞性拓扑优化设计问题。

本文中，基于BESO 法，将传统动态载荷优化法中的内外层迭代引入到ABAQUS-MATLAB 平台集成优化中，改进动态载荷拓扑优化流程，对子弹冲击下的夹芯拱结构进行拓扑优化设计和动力学响应分析，并与传统泡沫铝夹芯拱和实体拱进行对比。

1 ABAQUS-MATLAB 平台集成优化

利用BESO 方法进行ABAQUS-MATLAB平台集成优化流程如图1 所示，包括以下5 个步骤。

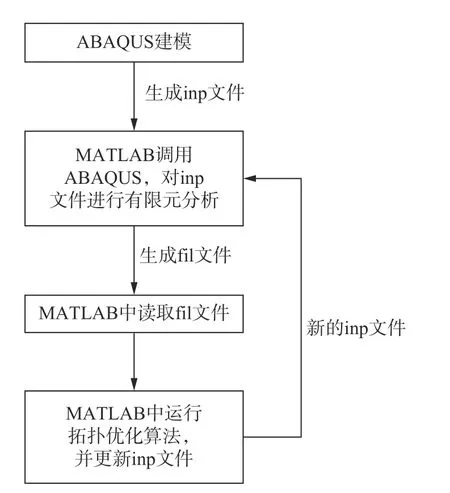
图1 ABAQUS-MATLAB 平台集成优化流程Fig. 1 ABAQUS-MATLAB platform integration optimization process

(1)在ABAQUS 中进行初始建模和网格划分，导出inp 文件作为优化目标文件。

(2)在MATLAB 中设置模型的优化参数：结构的体积分数、体积进化率和过滤半径等。

(3)算法中调用ABAQUS 进行有限元分析，读取结果fil 文件，并根据结果计算单元应变能灵敏度。

(4) 将更新后的结构信息写入inp 文件中，完成inp 文件的更新，用于下一次的有限元分析。

(5)重复上述步骤(3)～(4)，直至优化结果同时满足目标体积分数和收敛条件。

以最小柔度为目标函数、结构体积分数为约束条件，将设计域内的连续体结构离散为有限个单元。将每个单元的相对密度x（或1）设为优化设计变量，低效单元相对密度为，其他单元相对密度为1。利用有限元分析，计算得出低效的单元，并将其移除。通过设置删除率，并一步步删除设计域中的低效单元，来实现结构优化。其数学模型如下：

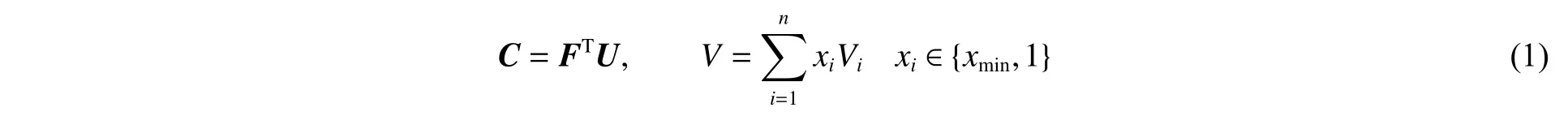
式中：为目标函数，即最小柔度值；和分别为结构的力和位移，=，为结构的刚度矩阵；为当前结构总体积；Vi 为第i 个单元的体积；n 为结构单元数；x为设计变量，是每个单元的相对密度；为相对密度的极小值；当x=时，第个单元为低效待删单元；当x=1 时，第个单元为实体单元。

2 等效静态载荷法

2.1 原理

在动态载荷的位移响应-时间图中，把时间分割成有限个时间点，将每个时间点与动态载荷产生相同位移的一组载荷集定义为等效静态载荷，如图2 所示。

从图2 可以看出，动载荷下结构的位移响应-可以与等效静载荷在每个时间段上的位移响应完全一致。动态载荷响应分析方程为：

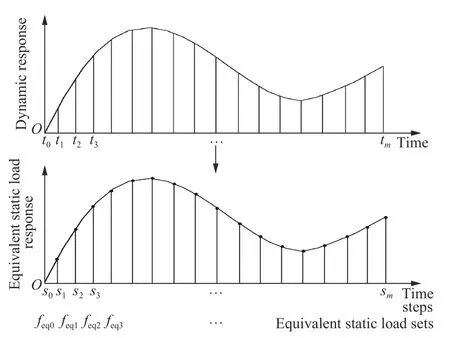
图2 静态载荷等效过程Fig. 2 Static load equivalent process

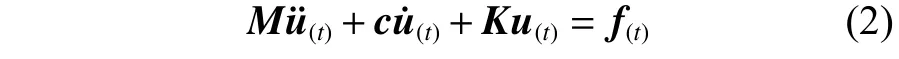
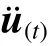
对式(2)进行变换，有：

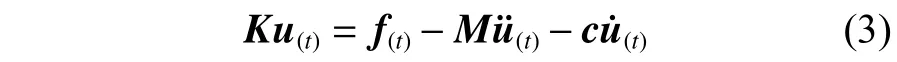
再对式(3)进行变换，将式(3)中的连续时间变量等效为等效静态载荷中个工况，可得：

式中：f和分别为第个时间点的等效静态载荷和位移。式(4)将非线性动力分析等效变换为个时间节点的线性静载优化。

2.2 基于BESO 法的等效静态载荷法

将建立的拓扑优化数学模型与等效静态载荷法结合，式(1)可改写为：

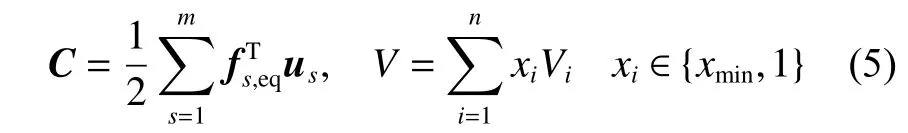
将上述优化模型应用于ABAQUS-MATLAB平台集成，图3 为等效静载的BESO 方法优化流程图。

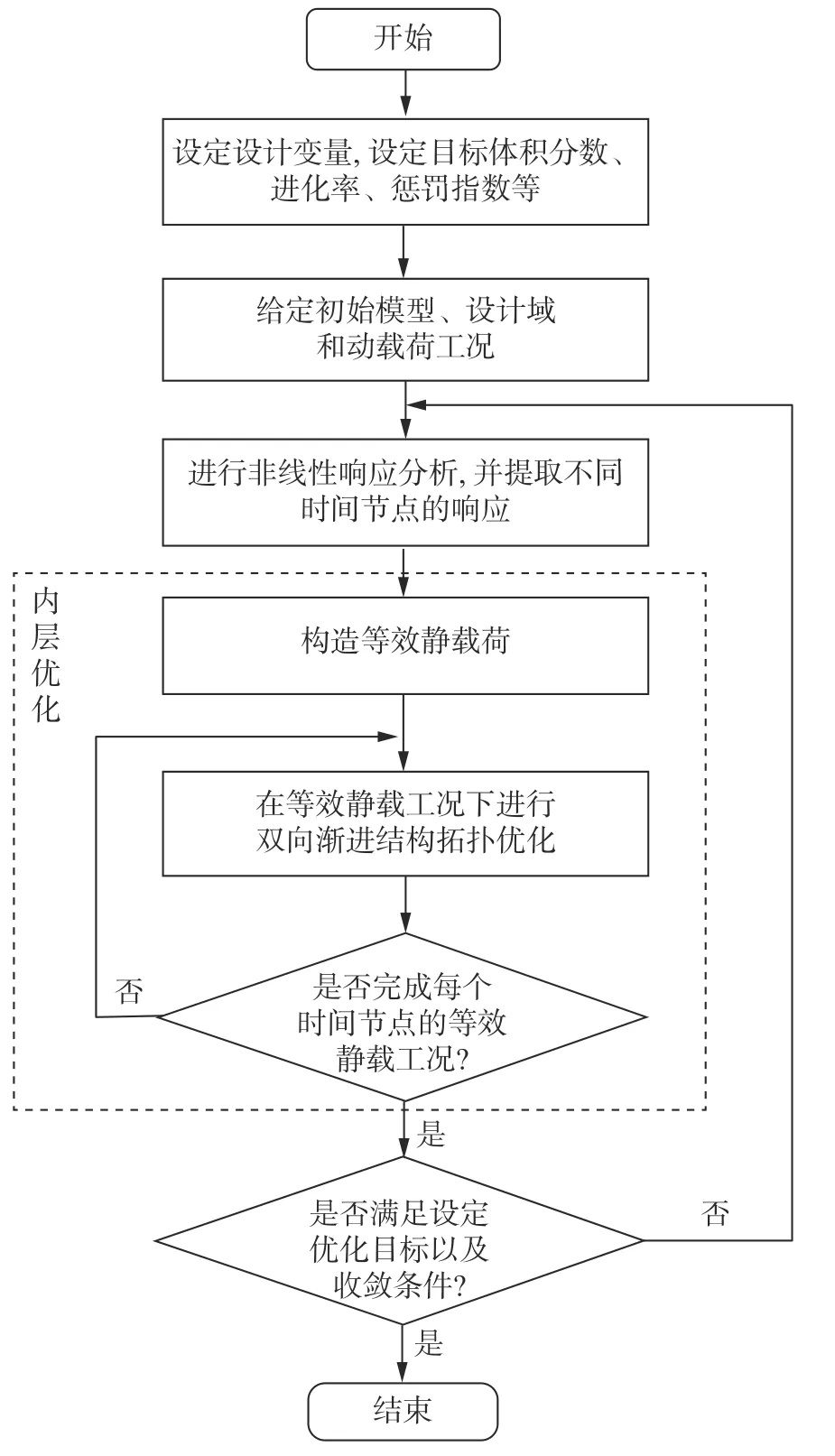
图3 优化流程Fig. 3 Optimized process

(1)先给定优化设计变量以及优化参数：目标体积分数、进化率和惩罚指数等。

(2)建立2 个相同的有限元初始模型：模型1为动态载荷工况，用于在ABAQUS 中进行非线性分析；模型2 为等效静载荷工况，用于MATLAB中进行双向渐进结构拓扑优化。采用双有限元模型虽然增加了平台之间的信息交互流程，但可以充分利用商业有限元软件强大的计算和前后处理能力，提高了计算精度，对几何结构较复杂的模型有更好的适用性。

(3)对模型1 在冲击载荷工况下进行非线性响应分析，并提取不同时间节点上的结构响应（接触力、加速度、速度)，构造与冲击载荷有相同位移场的等效静载荷f,=1,2,···,；由于结构受子弹冲击时，其外部动载荷未知，所以在获得等效静载荷之前，需要将子弹冲击载荷进行转化，如将其转化为接触力、子弹质量与其加速度乘积或者接触面初速度等，在MATLAB 与ABAQUS 信息交互中提取接触力数据转化为外部动载。

(4)将得到的等效静载荷作为模型2 的外载荷，在MATLAB 中利用双向渐进结构优化法进行拓扑优化，并在MATLAB 中进行内层优化迭代，直至完成每个时间节点的静态载荷工况。

(5)更新设计变量，将优化结果写入模型1，检测是否满足优化目标以及收敛条件。若满足，则结束；若不满足，则返回至步骤(3)。收敛条件为：

式中：ε为相对误差值，这里取0.01；为当前迭代次数；为自然数，通常取5。则式(6)表示过去10 步迭代中柔度的改变量应不超过0.01。

3 冲击载荷下夹芯拱结构的优化设计和响应分析

3.1 优化设计

冲击载荷是工程实际中较常见的外载荷。图4 为两端固支的拱形二维夹芯梁结构，在上面板中心处受到初速度=100 m/s 的子弹冲击，子弹宽度=5 mm。设计域是×=120 mm×20 mm的中间拱芯层，拱半径=185 mm；上、下面板为非设计域，面板厚度=1 mm；将中间设计域划分为122×20 个四边形单元，单元边长为1 mm。BESO 方法中通过敏度过滤技术来对过滤半径内其他单元的敏度值进行加权平均，以修正中心单元的灵敏度，减少网格依赖性，可以有效避免因网格尺寸不同导致优化结果的差异。

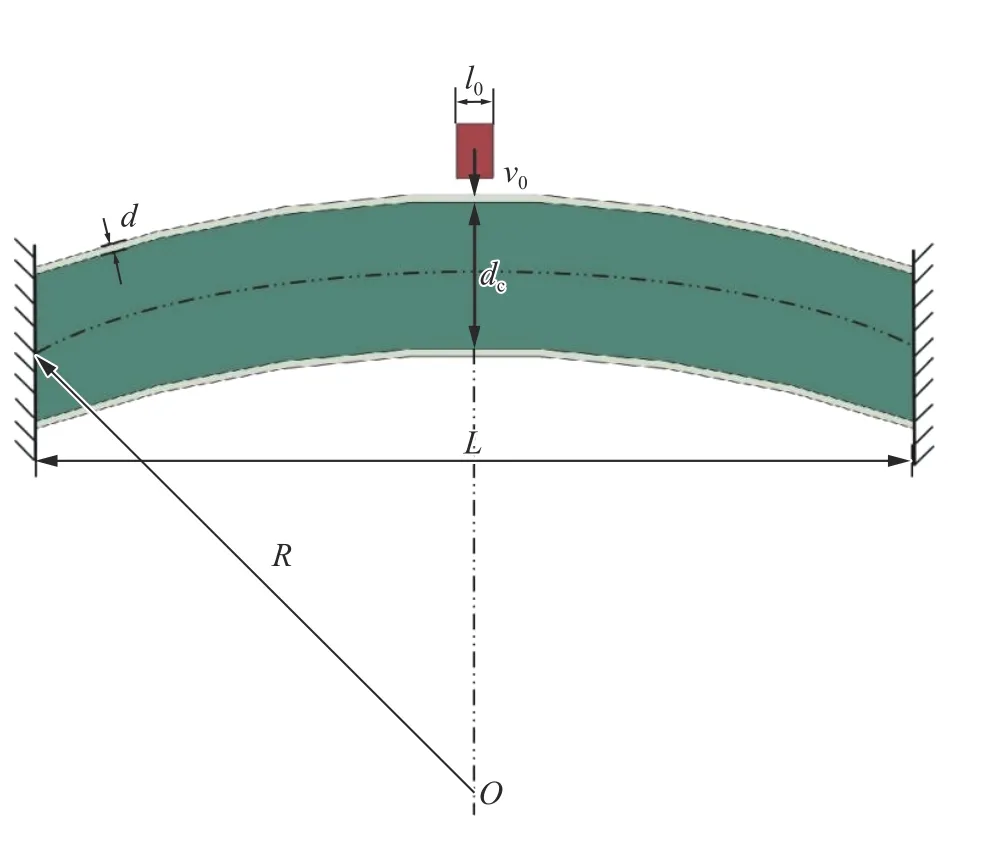
图4 冲击载荷下夹芯拱模型Fig. 4 The sandwich arch model under impact load

夹芯拱结构中间芯层和上、下面板材料都选择铝，其主要的力学性能参数：密度为2.7 g/cm，弹性模量为70 GPa，泊松比为0.3，屈服强度为80 MPa，剪切模量为700 MPa；子弹为密度为7.9 g/cm的刚体。整个优化过程中不考虑材料的失效和破坏。

主要优化参数：目标体积分数为0.5；删除率为0.03；过滤半径为3。

采用双向渐进结构拓扑优化方法中的软杀法进行结构优化，为了避免刚度矩阵奇异化，用较小的相对密度来表示灵敏度数值低的待删除单元的相对密度，如取=10作为待删除单元的相对密度，同时在优化过程中赋予这些单元较小的弹性模量。在后续的有限元分析中，为避免这些待删单元出现畸变，优化结束后在HyperMesh 中删去相对密度较小的单元。

最终的优化结果如图5 所示。芯层结构主要可分为3 个部分：中间区域A，主要呈现出类似三角点阵夹芯结构的构型；过渡区域B，主要呈现出Y 形构型；边界区域C，主要呈现C 形构型。优化后的夹芯拱结构体积为其初始结构体积的50%，降低了用料成本，减轻了自重，而且优化后的结构对称，在主要承受载荷的位置材料分布较密集，受力合理，也较美观。将优化结果称为模型O。

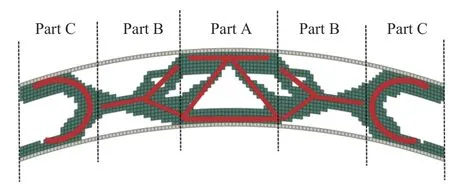
图5 芯层结构的优化结果Fig. 5 Optimization result of a sandwich structure

图6 为夹芯拱结构优化历程，夹芯拱结构经历25 步外层迭代后收敛完成，即进行了25 次非线性动力学分析，每次非线性冲击载荷被等效为25 次线性静载，整体优化过程较稳定。

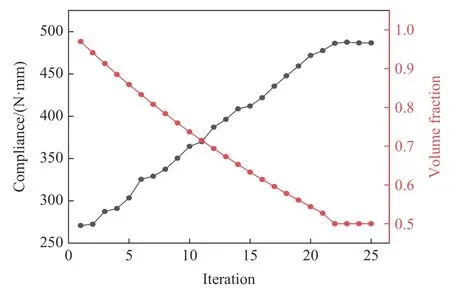
图6 夹芯拱结构优化历程Fig. 6 The process of sandwich arch structure optimization

3.2 最终的优化结果在冲击载荷下的动态响应

如图7 所示为冲击载荷下，夹芯结构根据上、下面板的速度特征，将芯层分为了2 种类型。图7(a)所示为硬芯层夹芯结构，其主要特征为：上面板速度随时间不断减小，下面板速度随时间不断增大，芯层在这一阶段持续压缩，当=时上、下面板速度达到一致，芯层不再压缩，上、下面板速度以相同频率减小。图7(b)所示为软芯层夹芯结构，其主要特征为：面板速度随时间不断减小，下面板速度随时间先增大，当=时下面板速度开始减小，当=时上、下面板速度达到一致，芯层不再压缩，上、下面板速度以相同频率减小。

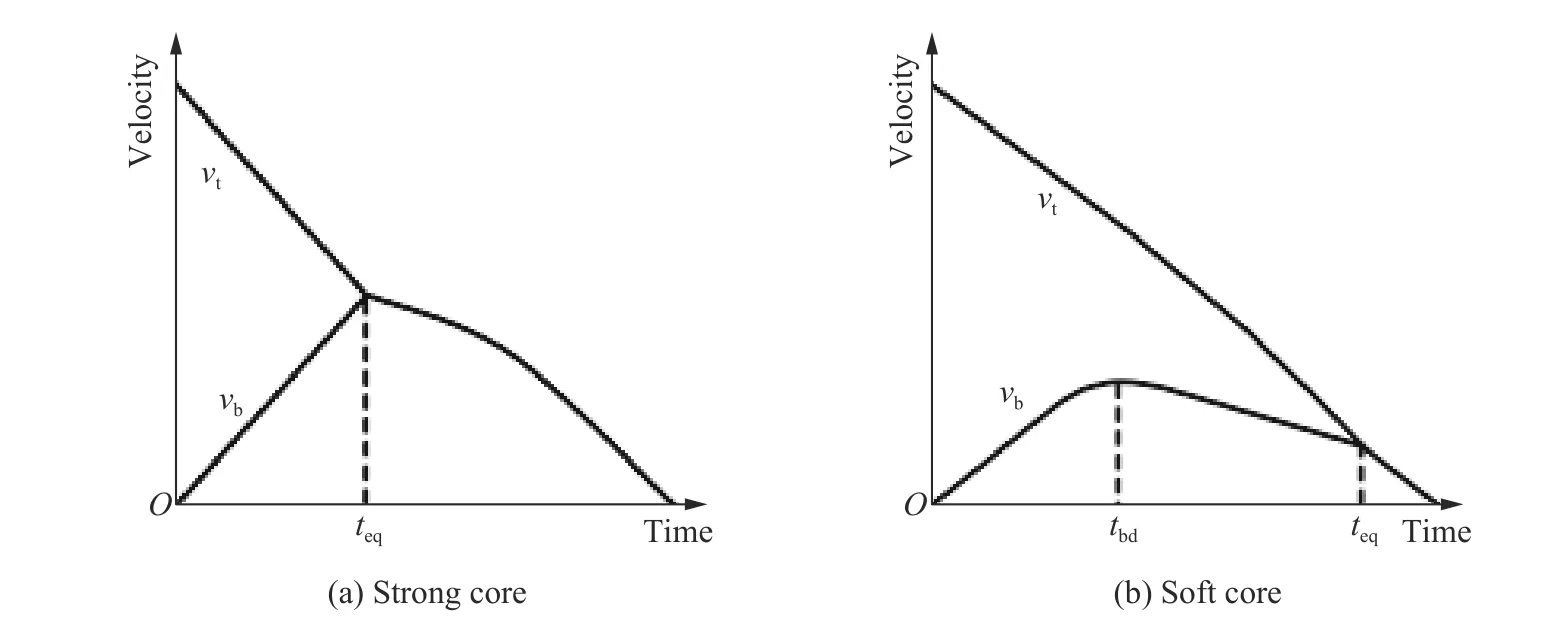
图7 不同类型芯层夹芯结构上、下面板速度时程曲线Fig. 7 Velocity versus time histories of the mid-span of the top and bottom panels for two types of sandwich response[34]

图8 为初速度=100 m/s、宽度=5 mm 的子弹冲击时，经过优化后的结构上、下面板速度时程曲线。从图8 可以看出，经过优化后的夹芯结构上、下面板的速度特征与图7(a)的芯层特征较接近，说明经过优化后的芯层就有较高的刚度。但同时可以看出，在上、下面板以共同的速度运动之前，速度曲线出现多次相交，这是由于芯层材料分布不均匀，由图5 可知，区域A 及与区域B 连接处材料分布较多，质量较大，受到惯性作用与弹性能释放的影响，下面板受到芯层的冲击作用较大。

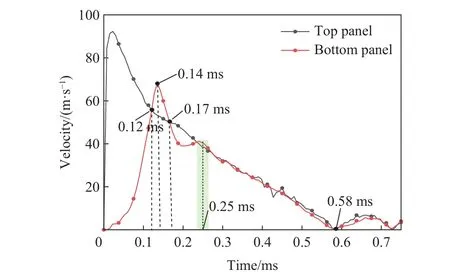
图8 经优化后的夹芯拱上、下面板速度时程曲线Fig. 8 Velocity-time curves of top and bottom panels of the optimized sandwich arch

优化结构的变形响应过程如图9 所示。当=0 ms 时，子弹开始作用于上面板；当=0.06 ms 时，子弹作用区域处面板出现明显的凹陷变形，结合图9 以及图5 可以看出，芯层中间区域A 承受较大压缩变形（图9 中蓝色区域），由于芯层的特殊结构，芯层的变形主要以区域A 上部凹陷，下部支撑受压向两侧扩展为主，此时下面板并未发生明显的变形。当=0.10 ms 时，压缩变形从A 区域下部支撑向结构边界两侧传播，A 区域下部横梁受拉开始变形，导致芯层区域B 发生以拉弯联合作用的为主的旋转变形模式，B 区域上面板向中部挤压，下面板向边界处挤压，均呈现出向上隆起的变形。当=0.12 ms 时，下面板的速度与上面板的相等。当=0.14 ms 时，下面板的速度达到最大值，此时下面板的速度高于前面板的。当=≈0.25 ms 时，区域B 处上、下面板隆起变形进一步增加，芯层C 区域上端出现拉伸变形，下端出现压缩屈曲变形模式，之后上、下面板以相同的速度运动；当=0.58 ms 时，上、下面板速度减小为0 m/s，上、下面板出现轻微的弹性回弹，结构整体在平衡位置（残余挠度）振动。

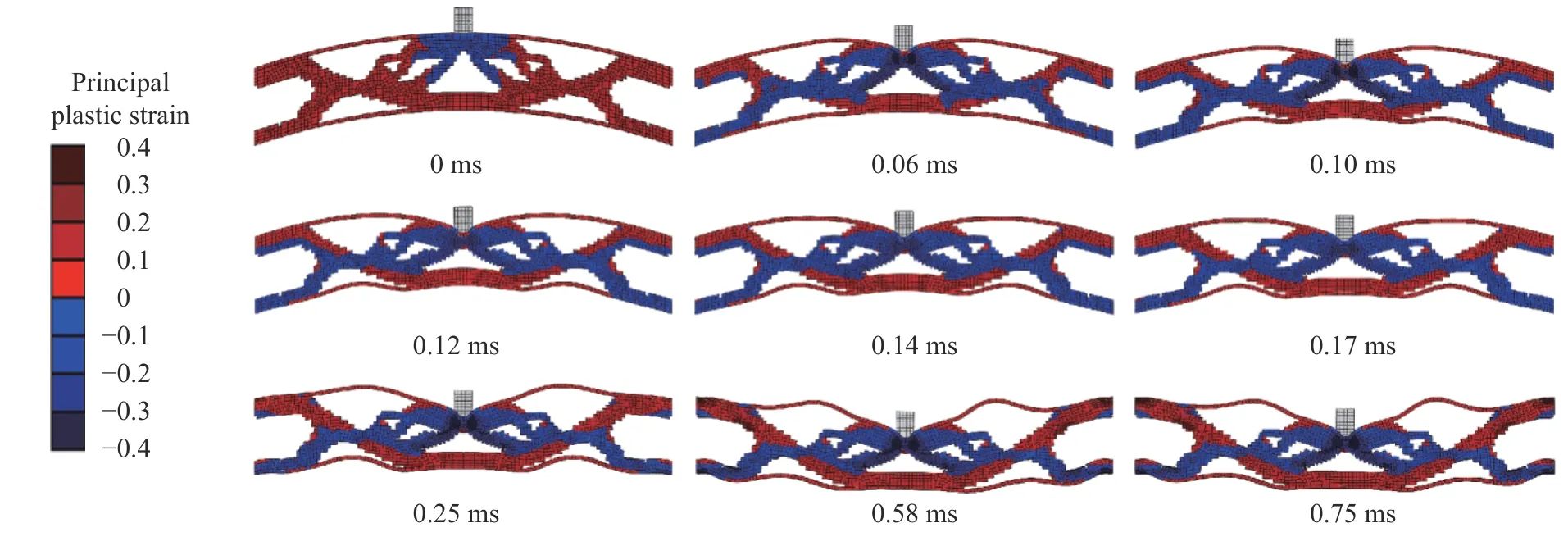
图9 经过优化后的结构在v0=100 m/s 子弹冲击下的响应过程Fig. 9 Response process of the optimized structure under the impact of a projectile with the initial velocity of 100 m/s

3.3 相同工况下优化结构与对照结构的响应分析

为了验证最终优化结果的抗冲击性能的优异性，对照模型A 选择Voronoi 泡沫铝夹芯拱模型，对照模型B 选择等质量的实体拱模型，如图10 所示。模型A 芯层泡沫铝的厚度为0.6 mm，泡沫铝体积为芯层总体积的50%，芯层与上、下面板之间定义为Tie 接触；为了研究对比芯层的吸能占比情况，在模型B 的实体拱中也分别对应设计了上、下面板，面板与实体芯层之间也采用Tie 接触的方式连接。2 种对照模型均选用与前述优化模型相同的材料属性，均不考虑材料的破坏与失效。

图10 所示的2 种对照模型，拱半径=185 mm，跨度=120 mm，上、下面板厚度=1 mm，子弹宽度=5 mm，初速度=100 m/s。模型A 泡沫铝芯层厚度=20 mm；模型B 实体芯层厚度=10 mm。2 种对照模型均采用四边形单元，单元边长为1 mm。

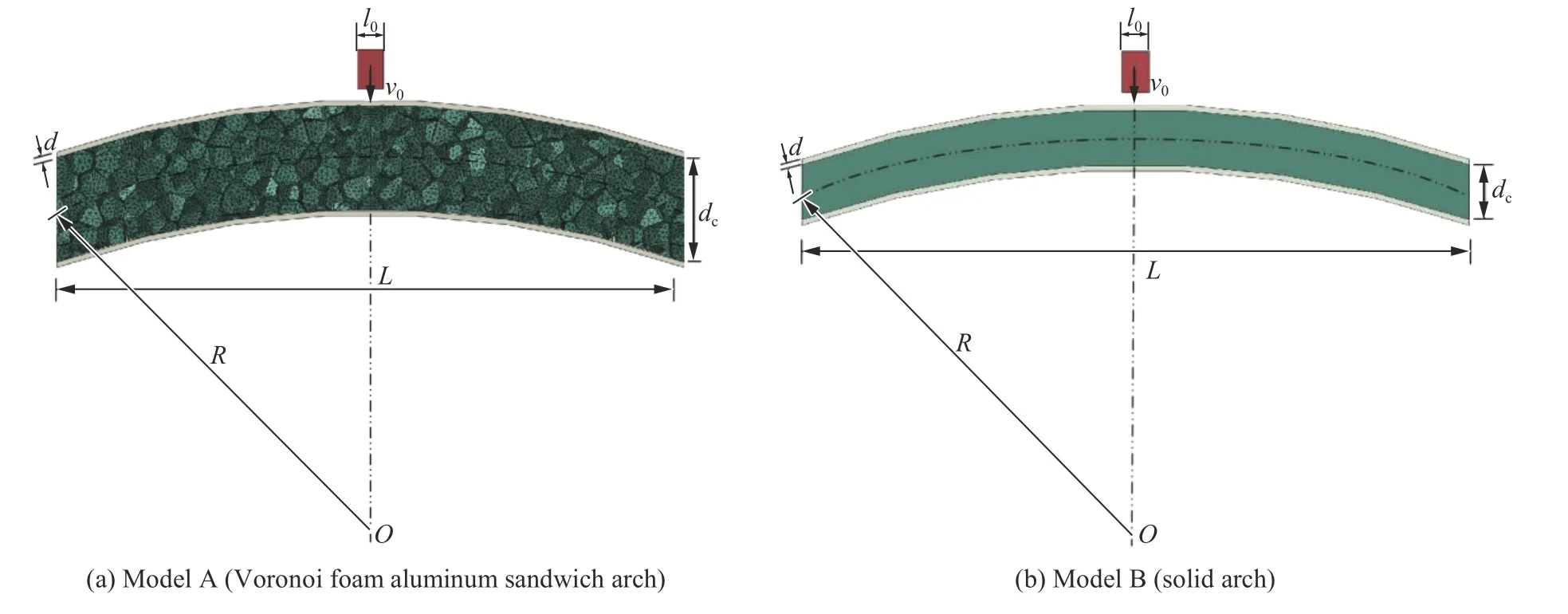
图10 2 种不同芯层等质量对照模型Fig. 10 Two different core models with equal mass

2 个对照模型上、下面板速度时程曲线如图11 所示，模型A 在==0.17 ms 时，上、下面板中心处的速度达到一致，面板与芯层开始以相同的速度向下运动，当=0.58 ms 时，上、下面板的速度降低为0 m/s，上、下面板出现轻微的弹性回弹；而对于实体拱模型B，当==0.04 ms 时，上、下面板中心处的速度便达到一致，芯层几乎无压缩，在=0.60 ms 时上、下面板速度降低为0 m/s，上、下面板开始轻微地弹性回弹。2 个对照模型的响应完全符合图7(a)的芯层特征。

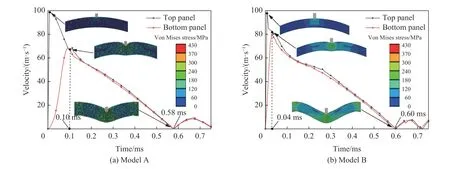
图11 两模型上、下面板速度时程曲线Fig. 11 Velocity-time curves of the top and bottom panels of two models

由于人体或者被保护的主体结构一般位于夹芯结构下（后）方，夹芯结构作为防护附层结构，一般可通过考察夹芯结构下面板的挠度和芯层的吸能来判断夹芯结构抗冲击性能优劣，图12 所示为最终优化结果与2 种对照模型在相同冲击载荷下上面板中心处的挠度随时间的变化曲线，从图中可以看出，经过优化后的结构上面板挠度最小，2 种对照模型上面板挠度几乎相同，上面板挠度达到峰值以后，会发生小幅的弹性回弹，从图11 变形模式可以看出，对照模型B 整体变形较大，而对照模型A 由于子弹压入芯层，造成上面板中心处位移较大。图13 为3 种结构下面板挠度-时程曲线。由图13(a)可知，经过优化后的结构下面板挠度最小，而对照模型B 下面板位移最大。图13(b)为0～20 µs 内，下面板中心处的挠度-时间曲线，由图可知，模型B 由于实体芯层，芯层无压缩，上、下面板中心处几乎同时开始产生位移，模型A 下面板中心处开始产生位移的时间为=11 µs，而经过优化后的结构下面板开始发生变形的时间最晚，为=15 µs。芯层压缩变形时间的增加，更有利于减小后面板受到的冲击作用，提高结构的能量吸收能力。

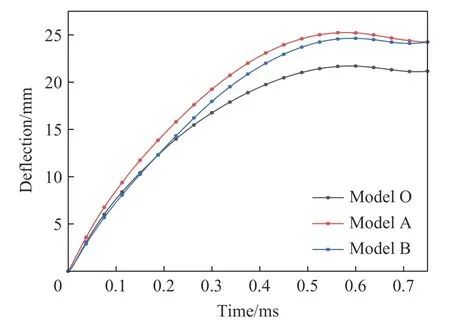
图12 上面板挠度-时间曲线Fig. 12 Deflection-time curves of top panles

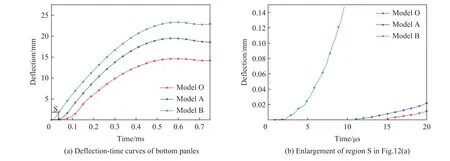
图13 下面板挠度-时间曲线Fig. 13 Deflection-time curves of bottom panels

由前面的分析可知，当初始冲击速度为100 m/s 时，经过优化后的夹芯拱具有较好的抗冲击性能，但在实际工程中的冲击载荷可能是多样的，针对单一工况的优化是否能满足不同工况的需求，必须经过进一步的验证。为此，图14 对比了3 种模型在初速度=20，50，80，100 m/s 的子弹冲击下的下面板的挠度和芯层的能量吸收。图14(a)为3 种模型下面板中心处的挠度对比，从图中可以看出：经过优化后的结构在不同初速度的子弹冲击下，下面板挠度均为最小。14(b)为在不同初速度的子弹冲击下，芯层的比吸能（=/，为芯层塑性耗散能，为芯层质量）情况，可以看到经过优化后的结构芯层比吸能均高于模型A 和模型B 的芯层比吸能。由于子弹刚性较大、冲击速度较高，可以忽略弹性段能量，芯层能量耗散直接采用其塑性耗散能量。

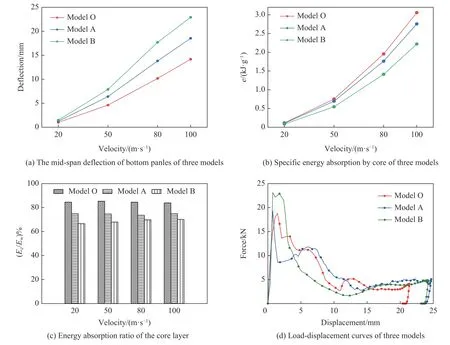
图14 3 种模型在不同速度冲击下的动态响应Fig. 14 Dynamic response of the three models at different impact velocities

由图14(c)可知：不同初速度的子弹冲击下，经过优化后的结构芯层吸能占比（芯层塑性能量耗散与总塑性能量耗散之比，即/）分别为84.6%、85.3%、84.5%和83.9%，模型A 的芯层吸能占比分别为74.9%、74.6%、73.6%和74.9%，模型B 的芯层吸能占比分别为66.6%、67.9%、69.8%和70.1%。对比以上各组数据可以发现：经过优化后的结构抗冲击性能最优，而对照模型A（Voronoi 泡沫铝夹芯拱模型）抗冲击性能次之，对照模型B（等质量实体拱模型）抗冲击性能最差。在相同的体积约束和载荷条件下，删除低效的单元而添加或保留高效的单元，有效地提高了材料的利用率，使得芯层每个部位都充分发挥作用；而对照组的结构中材料均匀分布，必然会导致某些部分的材料不能被充分利用，未起到抵抗变形的作用，材料合理分配使结构具有较好的抗冲击性能。在低速冲击下，几种结构的变形较小，结构的响应均未超过变形阈值，芯层结构受拉压弯扭转作用较小，一些部位未能充分发挥作用，所以优化后的结构抗冲性能优势并不明显；高速冲击下，优化后的结构能够充分发挥材料的性能，在本文研究的冲击载荷范围内，冲击速度越高，这种优势越明显。

较低的峰值冲击力和较高的平台力，代表了结构具有较好的吸能缓冲特性，也是评价结构抗冲击性能的一类指标。图14(d)为3 种模型在初速度=100 m/s 的子弹冲击下的力-位移曲线，从图中可以看出：当结构受到冲击时，在较短的行程内，冲击接触力迅速升高至峰值，随后下降至平台阶段，当子弹反弹后冲击接触力降为零。与随机泡沫铝夹芯拱（模型 A）相比，经过优化后，结构的冲击接触力峰值和平台阶段都较接近；与实体拱（模型 B）相比，经过优化后，结构的冲击接触力峰值下降约17.96%，同时平台阶段冲击接触力水平较高。

3.4 非对称载荷下优化结构响应分析

图15 为在初速度=100 m/s 的非对称载荷下的夹芯拱模型，子弹的偏移量=5 mm（与对称载荷相比，冲击点位置偏差 δ =/=1），其他模型尺寸与图4 模型相同。

图15 非对称载荷下夹芯拱模型Fig. 15 The sandwich arch model under asymmetric load

图16 所示为在非对称载荷下夹芯拱模型的优化结果，与图5 所示的优化结果相比，最大的区别在于结构的不对称，由于载荷作用部位偏向右侧，芯层左侧所受的拉压弯扭作用较小，低效单元较多，必然导致在芯层右侧单元分布较为密集；中心孔洞向左侧偏移，但结构仍然保持前者的一些基本特征，即过渡区域主要呈现C 形构型，左侧边界处也相应增加了杆件，以提高结构承载能力。

图16 非对称载荷下优化结果Fig. 16 Optimization result under asymmetric load

将非对称载荷下的优化模型称为模型N，将原对称载荷下的优化模型称为模型O，分析对比2 种优化结构与2 种等质量对照模型（模型A、模型B）在相同工况下的动态响应。图17 为在初速度=100 m/s 的子弹无偏移的冲击载荷下，4 种模型的动态响应对比。图17(a)为4 种模型上面板跨中处挠度时间曲线，从图中可以看出非对称载荷下的优化模型N 在子弹无偏差冲击下，上面板挠度大于优化模型O 而小于2 种对照模型，且有小幅弹性回弹；图17(b)所示为下面板跨中处挠度随时间变化曲线，可以看出2 种优化结构下面板挠度几乎相同，模型O 下面板最终挠度为14.19 mm，模型N 下面板最终挠度为14.28 mm，分析可知：在子弹冲击点位置偏差δ=1 时，在相同的对称冲击载荷下，优化模型N 的下面板挠度比模型O 下面板挠度仅增大0.6%；图17(c)所示4 种模型芯层比吸能对比，分析数据可知：在子弹无偏移冲击时，模型N 的比吸能仅比模型O 减小0.7%。

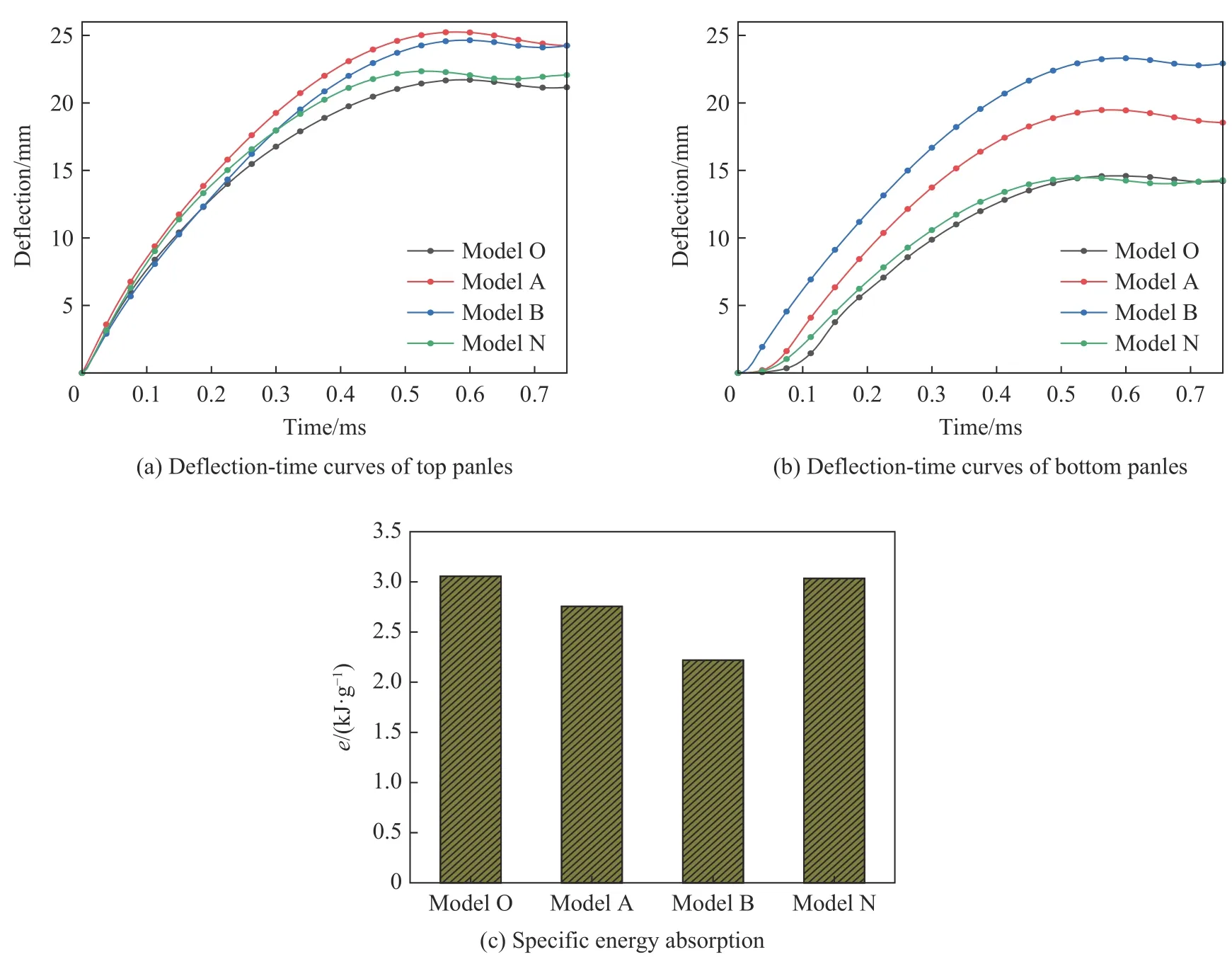
图17 4 种模型在子弹偏移量w=0 mm (δ=0）下的动态响应Fig. 17 Dynamic response of the four models under w=0 mm (δ=0) of a projectile

图18(a)与(b)所示为在子弹初速度=100 m/s，偏移量=5 mm 时，4 种模型上、下面板跨中处的挠度随时间变化曲线以及最终的响应结果，从图中可以看出：随着时间的变化，2 个模型上、下面板挠度不断增大，挠度达到峰值后都有轻微的弹性回弹，且模型O 的上、下面板跨中处挠度比模型N 面板跨中处挠度仅分别增大了4.4%和2.2%。图18(c)所示为4 种模型在子弹初速度=100 m/s，偏移量=5 mm 时芯层的比吸能情况对比，由图中数据分析可知：优化模型N 的芯层吸能占比略优于优化模型O，且优于2 种对照模型。由以上各组数据可得：在子弹偏移量=0 mm 时，优化模型O 的抗冲击性能、芯层吸能等略优于优化模型N，且2 种优化模型均优于对照模型；在子弹偏移量=5 mm 时，优化模型N 的以上性能略优于优化模型O，且均优于对照模型。从而表明：不同载荷工况下，最终的优化结果虽然稍有不同，每种工况下得到的优化结果在相应工况下所展现的力学性能也优于其他优化结构，并且对称优化结果在非对称载荷作用下，力学性能也优于等质量对照模型。

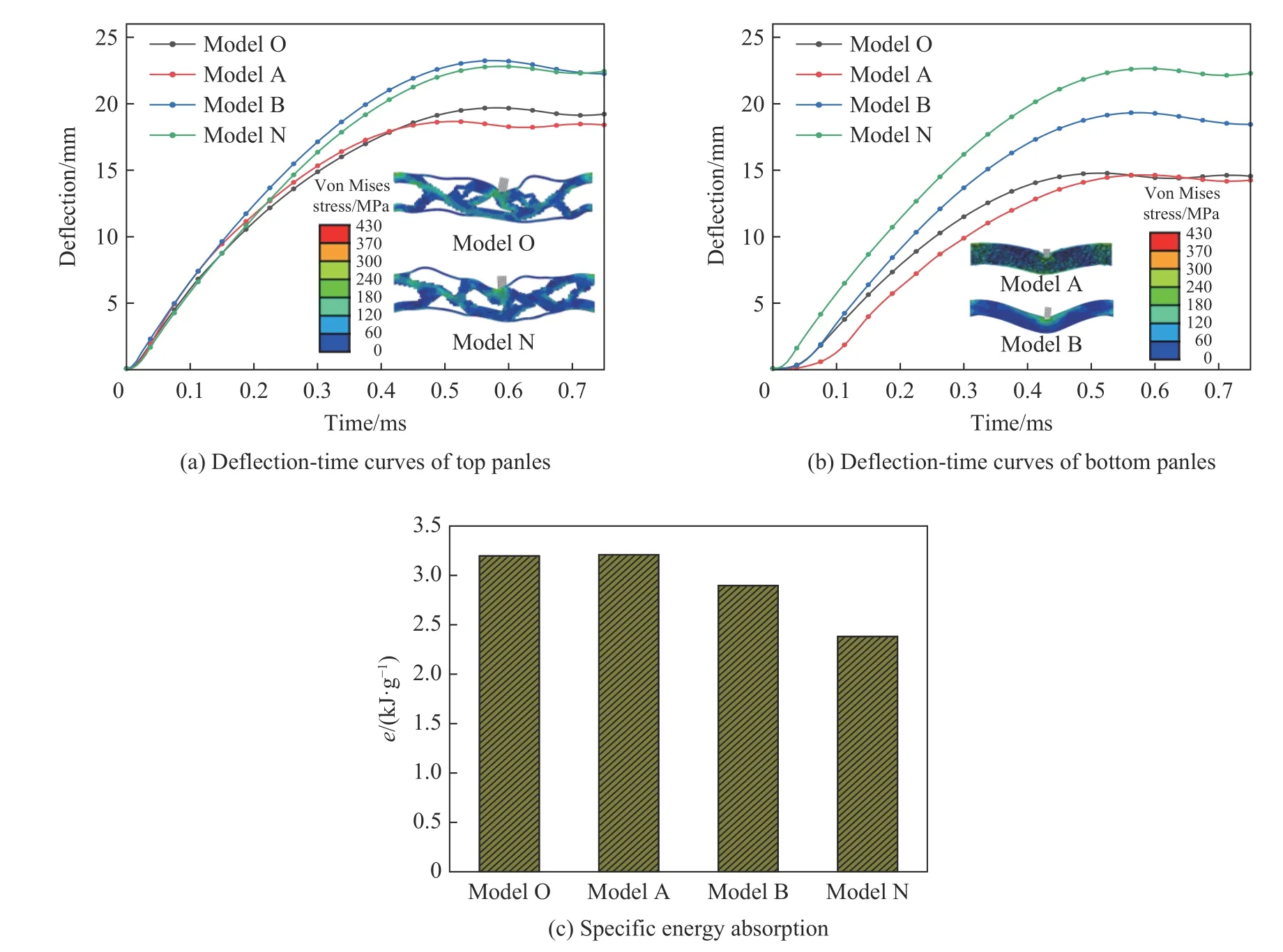
图18 4 种模型在子弹偏移量w=5 mm（δ=1）下的动态响应Fig. 18 Dynamic response of the four models under w=5 mm (δ=1) of projectile

以上分析充分说明，虽然结构在非对称冲击下，优化结果有差异，但在相同冲击载荷下，结构的响应特性与抗冲击性能相差较小，通过对称载荷对结构进行优化，具有一定的普适性，其结果在工程中具有较高的应用价值。

4 结 论

将等效静态载荷优化思想引入双向渐进结构拓扑优化方法中，基于双向渐进结构优化方法，改进了动态载荷拓扑优化流程，针对未知外部动载荷，在优化过程中对载荷进行了变换处理，增加了MATLAB 与ABAQUS 的信息交互过程，充分利用了商业有限元软件强大的计算和前后处理能力，提高了计算精度，对几何结构较为复杂的模型有更好的适用性。以夹芯拱芯层刚度最大化为目标，获得了冲击载荷下夹芯拱的最优拓扑构型，并与相同质量的Voronoi 泡沫铝夹芯拱、实体拱的动态响应进行了对比。

经过优化后的夹芯拱芯层可分为3 个对称的部分：跨中类三角点阵桁架结构区域、边界C 形结构区域以及跨中和边界之间的Y 形结构过渡区域。与等质量的Voronoi 泡沫铝夹芯拱、实体拱相比，在相同的冲击速度下，经过优化后的结构挠度最小，芯层比吸能最高；当冲击速度较低时，结构的响应均未超过变形阈值，芯层结构受拉压弯扭转作用较小，一些部位未能充分发挥作，经过优化后的结构的抗冲击性能优势并不明显；在所研究的冲击速度范围内，冲击速度越高，经优化后的结构的抗冲击性能越好。

对初速度=100m/s、子弹偏移量δ=1 子弹冲击下的夹芯拱结构进行优化设计，并对比了对称冲击与非对称冲击下2 种优化模型的动态响应。当结构受到对称冲击载荷时，在对称冲击载荷下获得优化结构的抗冲击性能、芯层吸能等略优于在非对称载荷下获得的优化结构。当结构受到非对称冲击载荷时，在非对称载荷下获得优化结构的性能略优于在对称冲击载荷下获得优化结构的。但在2 种冲击载荷下，经过优化后所得结构的性能均优于对照模型。从而表明：不同载荷工况下，最终的优化结果虽有所不同，每种工况下得到的优化结果在相应工况下所展现的力学性能也优于其他结构，但在相同冲击载荷下，2 种优化所得结构的响应特性和抗冲击性能相差较小；通过对称载荷对结构进行优化，具有一定的普适性。