考虑尺寸效应的典型钻地弹侵彻混凝土深度分析*
2022-07-11程月华姜鹏飞谭可可
程月华,姜鹏飞,吴 昊,谭可可,方 秦
(1. 同济大学土木工程学院,上海 200092;2. 中国人民解放军96911 部队,北京 100011;3. 陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)
军事防护和民防工程面临钻地弹打击的威胁,而混凝土是上述工程广泛采用的建筑材料。因此,钻地弹冲击混凝土的终点弹道效应研究一直是武器研发和防护工程设计人员关注的重点。准确预测钻地弹以不同速度打击不同强度等级混凝土的侵彻深度,可为防护结构设计提供重要依据。
目前弹体侵彻混凝土的终点弹道参数研究主要有试验和数值模拟2 种手段。学者们基于野外开展的中等口径至大口径弹体冲击试验,拟合出相应的侵彻经验公式,如修正的Petry 公式、BRL 公式、ACE 公式、修正的NDRC 公式、Ammann-Whitney 公式、Whiffen 公式、Kar 公式、UKAEA 公式、Haldar-Hamieh 公式、Adeli-Amin 公式、Hughes 公式、Healey-Weissman 公式、IRS 公式和Chang 公式等。此外,Forrestal 等、Frew 等和Chen 等分别基于空腔膨胀理论和缩比的小直径弹体侵彻试验提出了预测弹体侵彻深度的经典半经验侵彻公式。Rosenberg 等基于恒阻力侵彻模型提出了刚性弹侵彻和贯穿混凝土靶体的分析方法。数值模拟方法可全面综合地再现弹体侵彻过程并提供常规试验观测手段无法获得的靶体响应数据。Holmquist 等、Taylor 等、Riedel 等和Kong 等分别选用Holmquist-Johnson-Cook (HJC)、Taylor-Chen-Kuszmaul、Riedel-Hiermaier-Thoma (RHT)、修正的HJC、修正的Karagozian & Case 和Kong-Fang 材料模型来描述混凝土的力学性能,以预测弹体的侵彻深度、残余速度和靶体的开坑及剥落震塌等。
上述方法对预测原型钻地弹侵彻混凝土深度主要存在以下不足:(1)野外试验较多采用侵彻能力较弱的低阻式爆破弹,且混凝土强度较低,因此拟合出的经验公式对深侵彻钻地弹和高强混凝土靶体的适用性值得商榷;此外,现有公开发表的弹体直径大于100 mm 的侵彻试验中弹体长径比范围为1.92~3.30,普遍小于钻地弹长径比(>6),其侵彻能力也与真实钻地弹存在一定差距。(2)由于弹体侵彻混凝土存在尺寸效应,即利用小尺寸弹体试验结果预测大尺寸弹体侵彻深度时往往会出现较大的偏差,且尺度比例越大,偏差越大,具体分析见第1 节。因此,上述基于中小口径弹体侵彻试验提出的半经验侵彻公式并不适用于预测新型钻地弹的侵彻深度,详见第3 节。(3)数值模拟方法虽可建立新型钻地弹有限元模型并进行侵彻深度分析,但数值模型中涉及的材料模型和参数具有较强的复杂性和不确定性。此外,由于模型中较常选用的Lagrange 算法具有网格敏感性且在计算过程中需引入删除准则避免单元过度畸变,在综合考虑计算效率和计算结果准确性的情况下,原型钻地弹侵彻效应模拟中的删除准则需由大口径弹体侵彻试验进行标定。
本文中,首先,基于已有试验数据,分析引起弹体侵彻混凝土尺寸效应的原因;其次,为准确评估大口径原型钻地弹的侵彻深度,开展5 发100 和203 mm 口径缩比钻地弹侵彻普通和高强混凝土试验;然后,通过建立二维轴对称有限元模型进行数值模拟分析并与试验结果进行对比,验证有限元模型和算法的可靠性;最后,基于验证的有限元模型确定美军5 种钻地弹在不同打击速度(100~600 m/s)和不同强度混凝土(C40~C200)中的侵彻深度。
1 钻地弹侵彻混凝土的尺寸效应及其原因
弹体侵彻混凝土靶体的尺寸效应是指几何相似的弹体冲击混凝土靶体时产生不成比例的侵彻深度,即不满足相似律。吴飚等开展了7 发直径为10.1~203.0 mm 的几何相似弹体(见图1)以450 m/s的速度侵彻C40 和C60 混凝土靶体试验,试验结果表明,弹体侵彻混凝土深度有着明显的尺寸效应,如图2 所示。

图1 试验弹体[28]Fig. 1 Test projectiles[28]

图2 几何相似弹体无量纲侵彻深度随弹径的变化[28]Fig. 2 Non-dimensional penetration depths of geometrically similar projectiles varying with projectile diameter[28]
Forrestal 等和Frew 等分别开展了弹体直径为76.2 mm、最大粗骨料粒径为9.5 mm 的侵彻试验。通过将试验数据与文献[15]中所提出的Forrestal 半经验公式计算曲线进行对比,发现试验值均大于按相似律计算得到的结果,即不满足相似律,如图3 所示,其中为弹体冲击速度,ψ 为弹体头部曲径比。

图3 试验数据[29-30]与Forrestal 公式[15]对比结果Fig. 3 Comparisons of test data[29-30] and Forrestal formula[15]
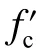
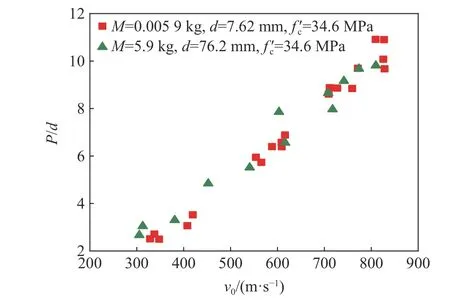
图4 Canfield 等[31]侵彻试验数据Fig. 4 Penetration test data by Canfield, et al[31]
徐建波开展了直径分别为10 和20 mm 的2 种完全几何相似弹体侵彻相同砂浆靶(不含粗骨料)的试验,结果见图5,可以发现侵彻深度完全满足相似律,图中为混凝土的标准立方体抗压强度。
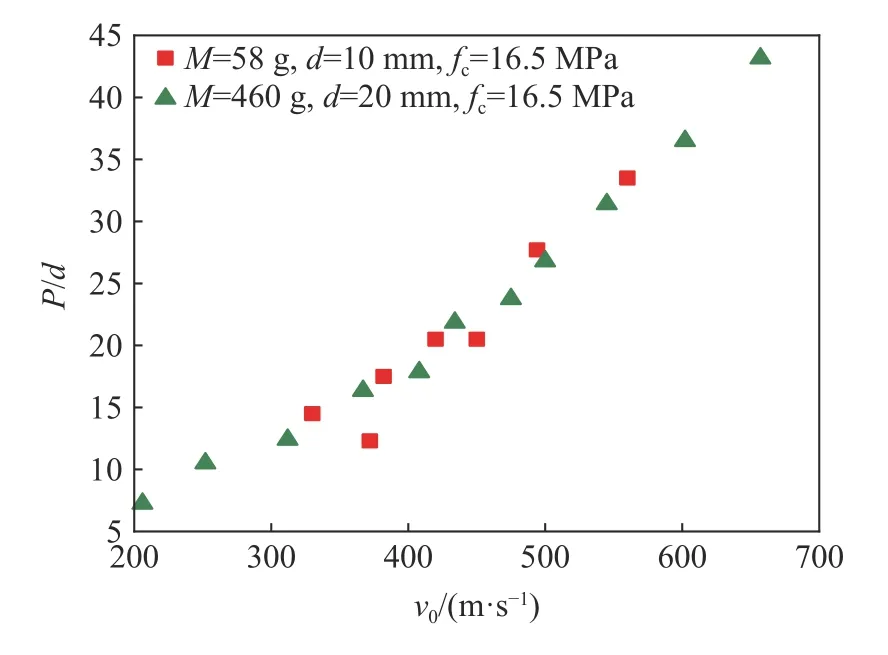
图5 徐建波[32]侵彻试验数据Fig. 5 Penetration test data by Xu Jianbo[32]
此外,为深入探讨弹体侵彻混凝土靶体的尺寸效应,Wu 等和彭永等分别建立了三维和二维细观混凝土有限元模型,模型中保持砂浆强度和骨料粒径不变,同比例缩放混凝土靶体和弹体尺寸,计算结果表明:在相同冲击速度下,大直径弹体的无量纲侵彻深度明显高于小直径弹体的。
基于上述对靶体参数一致,仅缩放弹体尺寸的试验和数值模拟工作、弹体和靶体参数同时缩放的试验以及几何相似弹体侵彻砂浆靶体试验的分析,可以得出,几何相似弹体侵彻混凝土靶体深度的尺寸效应主要是由于弹体和粗骨料粒径比值不一致引起的,即粗骨料粒径未随弹体尺寸进行同时缩放。采用由小口径弹体侵彻试验得到并验证的半经验侵彻公式,会高估粗骨料的贡献,使大口径弹体侵彻深度预测值明显低于试验值,这对防护工程设计偏于危险。如图2 所示,弹体以450 m/s 速度侵彻C40 混凝土,203.0 mm 直径弹体的无量纲侵彻深度较10.1 mm 直径弹体相应值偏大1.86 倍。上述结论也为缩比弹体侵彻试验中混凝土靶体浇筑时骨料粒径选取提供了要求和依据。
2 大口径弹体侵彻试验及数值模拟分析
考虑到尺寸效应对侵彻深度的影响以及原型侵彻试验的成本,开展大比尺缩比钻地弹的侵彻试验对研究钻地弹侵彻深度显得尤为必要。然而,通过对文献[15-16, 26-30, 32, 35-53] 中389 发侵彻试验进行总结,直径大于100 mm 的弹体仅有13 发,且其长径比(见图6)普遍小于原型钻地弹长径比,相应的混凝土靶体强度标号低于C60。

图6 试验弹体[26-27]Fig. 6 Test projectiles[26-27]
因此,本文中针对某原型钻地弹缩比设计了直径为100.0、105.0 和203.0 mm 的弹体共计5 发,见图7,试验中弹体采用经改装的制式火炮和自主研发平衡炮进行发射,弹体直径与炮管内径一致。靶体为C40 和C100 混凝土,测试得到立方体抗压强度分别约为40 和100 MPa。3 种尺寸弹体对应的圆柱体靶体尺寸分别为 ∅ 2 000 mm×1500mm、 ∅ 2500 mm×2 000 mm 和∅ 4000 mm×2000 mm。通过在炮口和靶板间放置测速网靶,记录弹体的发射速度。试验后对弹体进行回收并测量靶板的破坏情况,结果列于表1。图8 为试验布置及试验后典型的弹靶图片,可以看出靶体表面为米字形破坏,背面无损伤;弹体仅在头部发生轻微的磨蚀,整体并未发生明显变形。

图7 弹体几何尺寸(单位:mm)Fig. 7 Geometrical sizes of the projectiles (unit: mm)

图8 典型的试验布置及弹靶损伤Fig. 8 Typical test setup, and damaged targets and projectiles
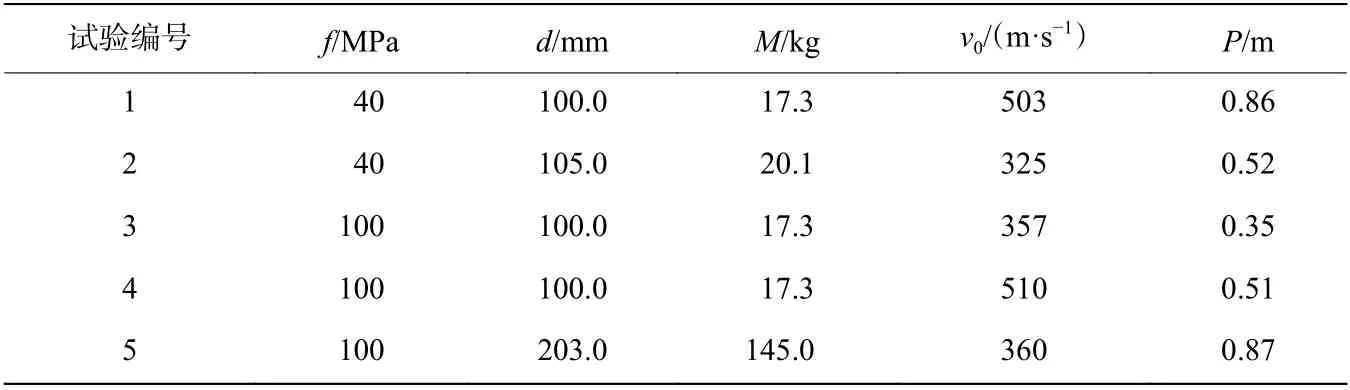
表1 试验结果Table 1 Test results
弹体侵彻问题的数值模拟中,靶体通常选用Lagrange 算法,其单元尺寸和相应的侵蚀应变对结果影响显著。下面先基于LS-DYNA 有限元软件,对表1 中105.0 mm 口径弹体侵彻C40 混凝土靶体和100.0 mm 口径弹体以357 m/s 侵彻C100 混凝土靶体的2 发试验进行数值模拟,确定单元尺寸和相应的侵蚀应变。再通过剩余的3 发试验数据和文献[28]中开展的100.0、152.0 和203.0 mm 口径弹体侵彻C40 混凝土靶体试验数据,对模型和算法进行充分验证。
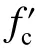
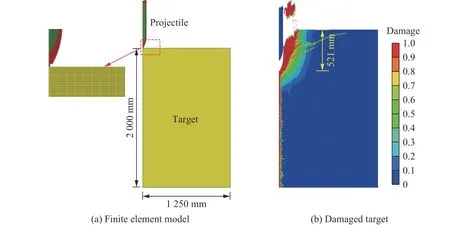
图9 二维轴对称有限元模型Fig. 9 Two-dimensional axisymmetric finite element model
基于上述确定的参数,进一步对剩余的3 发试验和文献[28]中的试验进行数值模拟,对比结果如图10所示。可以看出,预测结果与试验结果的相对误差小于9.4%,再次验证了所确定的混凝土材料模型参数及数值模拟算法的适用性和可靠性。

图10 数值模拟结果与试验结果对比Fig. 10 Comparison of the numerical simulation and test results
3 不同速度下典型钻地弹侵彻深度
3.1 典型钻地弹参数
本文中主要考虑5 种美军典型钻地弹战斗部:BLU-109B、BLU-113、BLU-122、WDU-43B 和SDB。鉴于战斗部侵彻混凝土结构时几乎不发生变形,其内部具体结构和尺寸对侵彻深度结果影响很小,因此,仅将文献[56-57]中给出的相关参数列于表2,表中为长度,为壁厚,BLU-122 弹头形状为双锥形,半锥角分别为21°和7°。
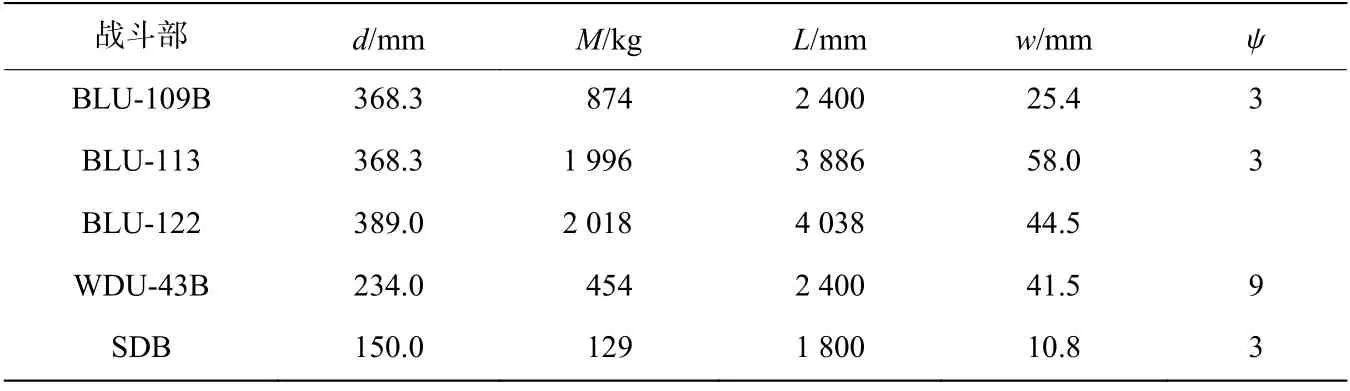
表2 5 种战斗部参数Table 2 Parameters of five warheads
3.2 侵彻深度计算公式
现有经典的经验和半经验侵彻深度计算公式主要有下列7 种。
(1)美国陆军工程兵团提出的ACE 公式为:
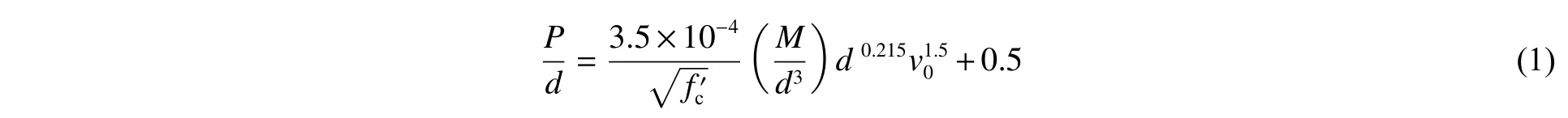
(2)在ACE 公式的基础上,美国国家防护研究委员会结合大量试验数据提出了NDRC 公式:
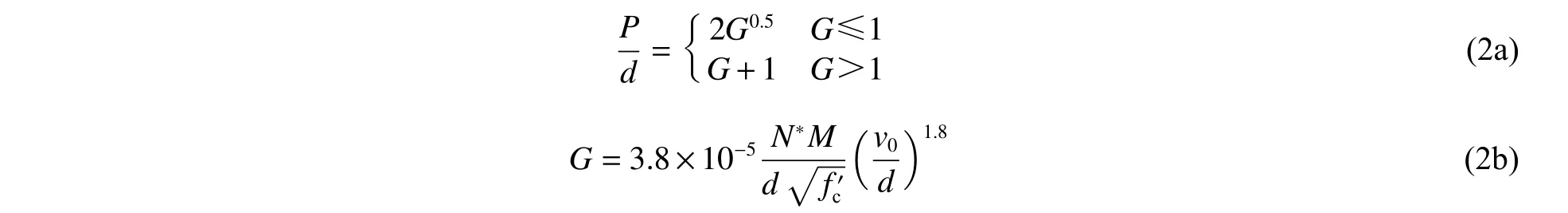
式中:为弹头形状系数,对于平头、半球、钝头和尖头弹体,分别为0.72、0.84、1.00 和1.14。
(3)Whiffen 公式中以(/)来考虑最大粗骨料粒径对尺寸效应的影响:

(4)对于半经验侵彻公式,Forrestal 等提出:
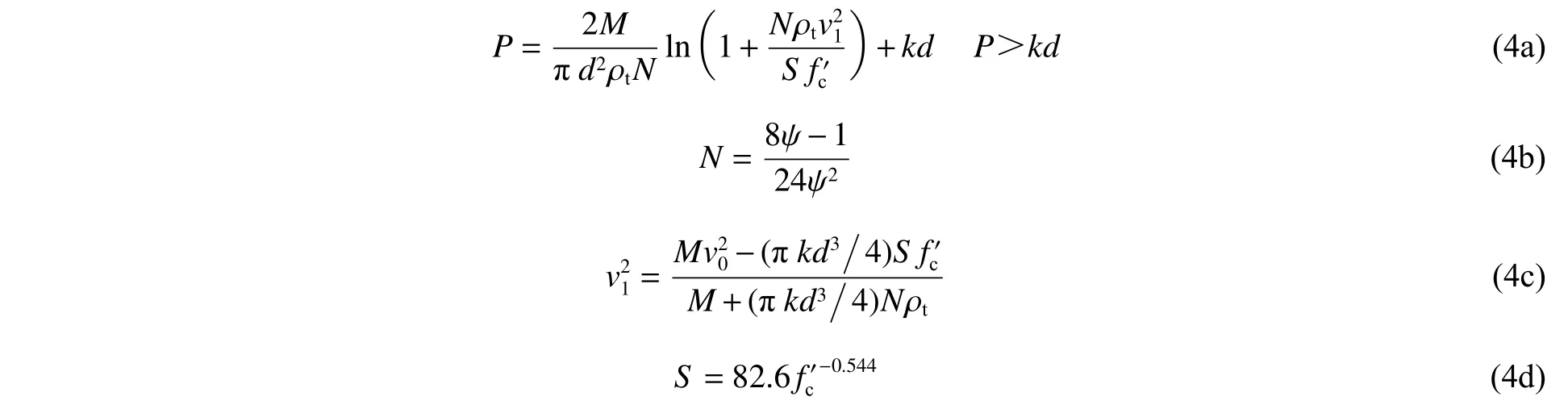
式中:ρ为混凝土密度;为开坑深度,=2基于试验数据得到;为弹头形状系数;ψ =/为弹体头部曲径比 ,为弹头部曲率半径;为无量纲常数,表示混凝土的抗侵彻性能,由抗压强度为13.5~ 96.7 MPa的砂浆和混凝土靶侵彻试验数据拟合得到;为弹体从弹坑开始进入弹道时的速度。(5)进一步考虑弹头形状的影响,Chen 等修正的Forrestal 公式为:

式中:=0.707+/,为弹头长度;为弹头形状系数,考虑了尖卵形、锥形、球形、钝形和平头。
(6)基于动态空腔膨胀理论,Peng 等提出了一个简单的统一化侵彻模型,其中靶体阻力项考虑了弹体直径与最大粗骨料粒径比值的影响:
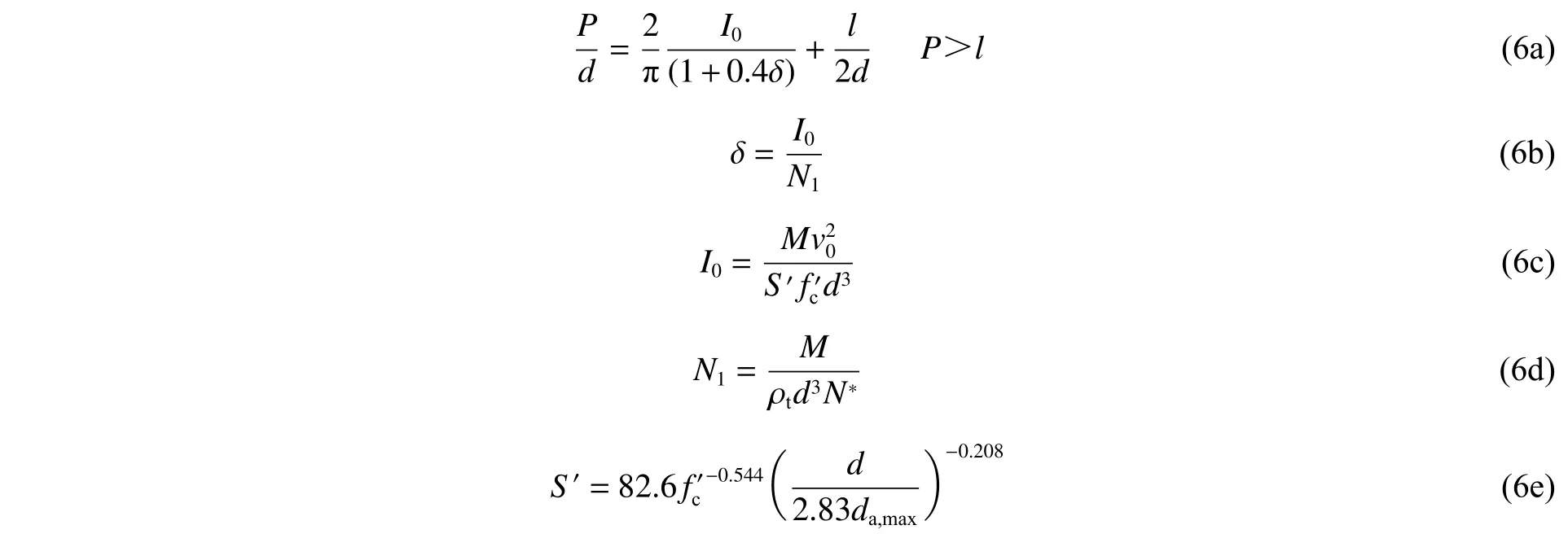
式中:为弹体头部长度。
(7)修正的Rosenberg 公式同样考虑了弹体直径和最大粗骨料粒径对侵彻深度的影响:
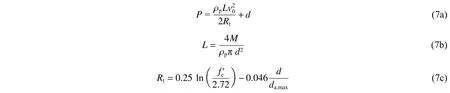
式中:ρ为弹体的材料密度。

考虑到表2 中5 种战斗部均为机/舰载战斗部,打击速度约为音速。因此,采用第2 节中验证的数值模拟算法和模型参数,预测得到了5 种美军典型战斗部在100~600 m/s 的侵彻速度下对C40 和C100 混凝土的侵彻深度,见图11~12。基于第2 节的计算方法,上述计算结果是合理可信的。此外,图11~12中部分预测结果也得到了原型弹体侵彻试验的验证。下面进一步基于预测的结果,对上述6 个经验和半经验侵彻深度计算公式的适用性进行评估。
3.3 C40 混凝土侵彻深度
图11 给出了侵彻速度为100~600 m/s 时由本文方法和侵彻公式得到的5 种典型战斗部无量纲侵彻深度。可以看出:ACE 公式、Whiffen 公式在所关注的速度范围内可较好地预测BLU-109B、BLU-113、BLU-122、WDU-43B 等4 种战斗部的侵彻深度,尤其对于音速附近,即300~400 m/s 时,2 个经验公式的预测相对误差最大为−13.7%。NDRC 公式在所关注速度范围内低估了战斗部侵彻深度;Peng 公式则在速度接近600 m/s 时对5 种战斗部的预测结果较好;Forrestal 公式和Chen 公式低估了BLU-109B、BLU-113、BLU-122、WDU-43B 等4 种较大口径战斗部的侵彻深度,而对于SDB 战斗部则预测结果较好。
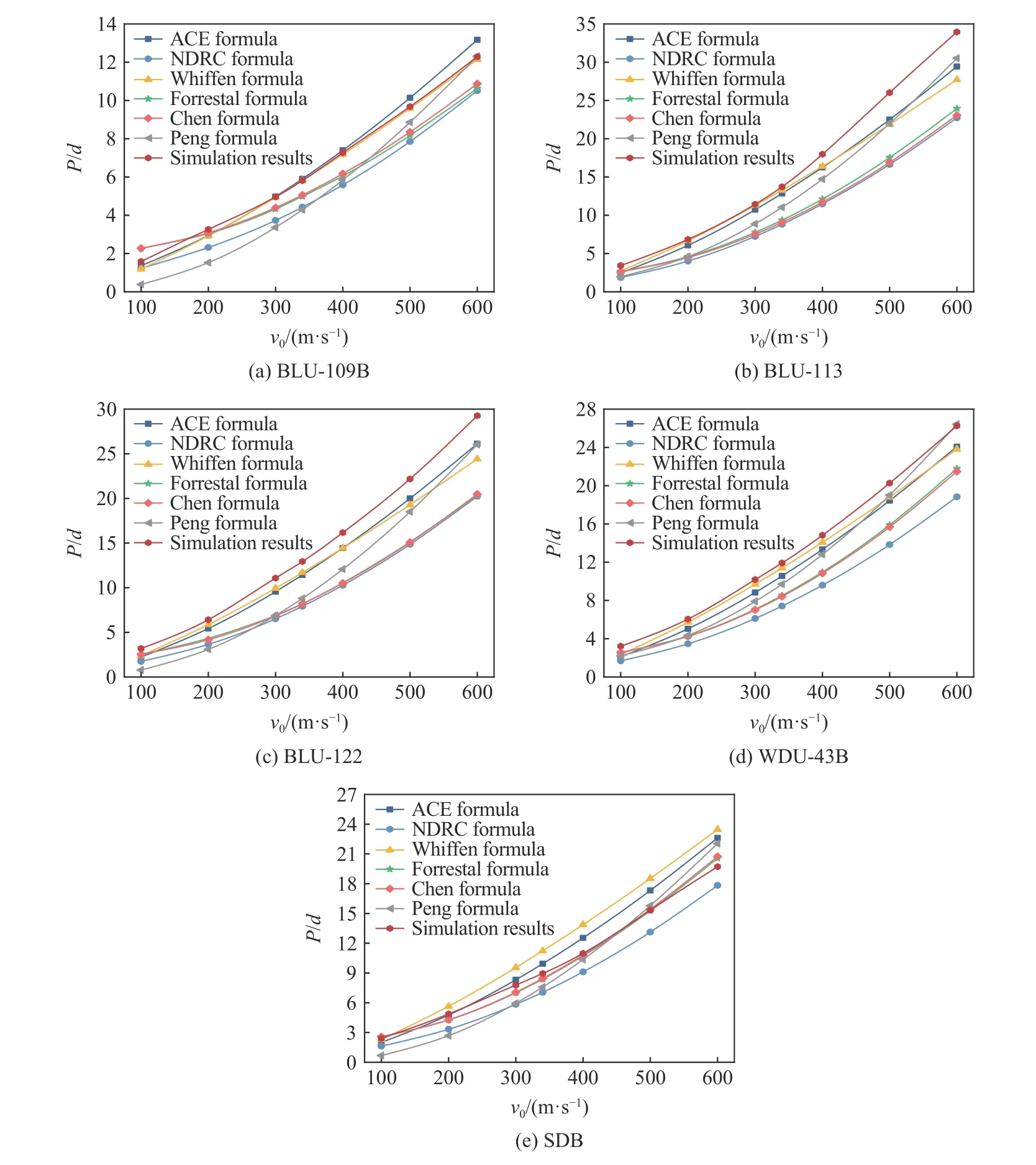
图11 C40 混凝土中5 种战斗部的无量纲侵彻深度Fig. 11 Non-dimensional penetration depths of five warheads into C40 concrete
3.4 C100 混凝土侵彻深度
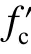
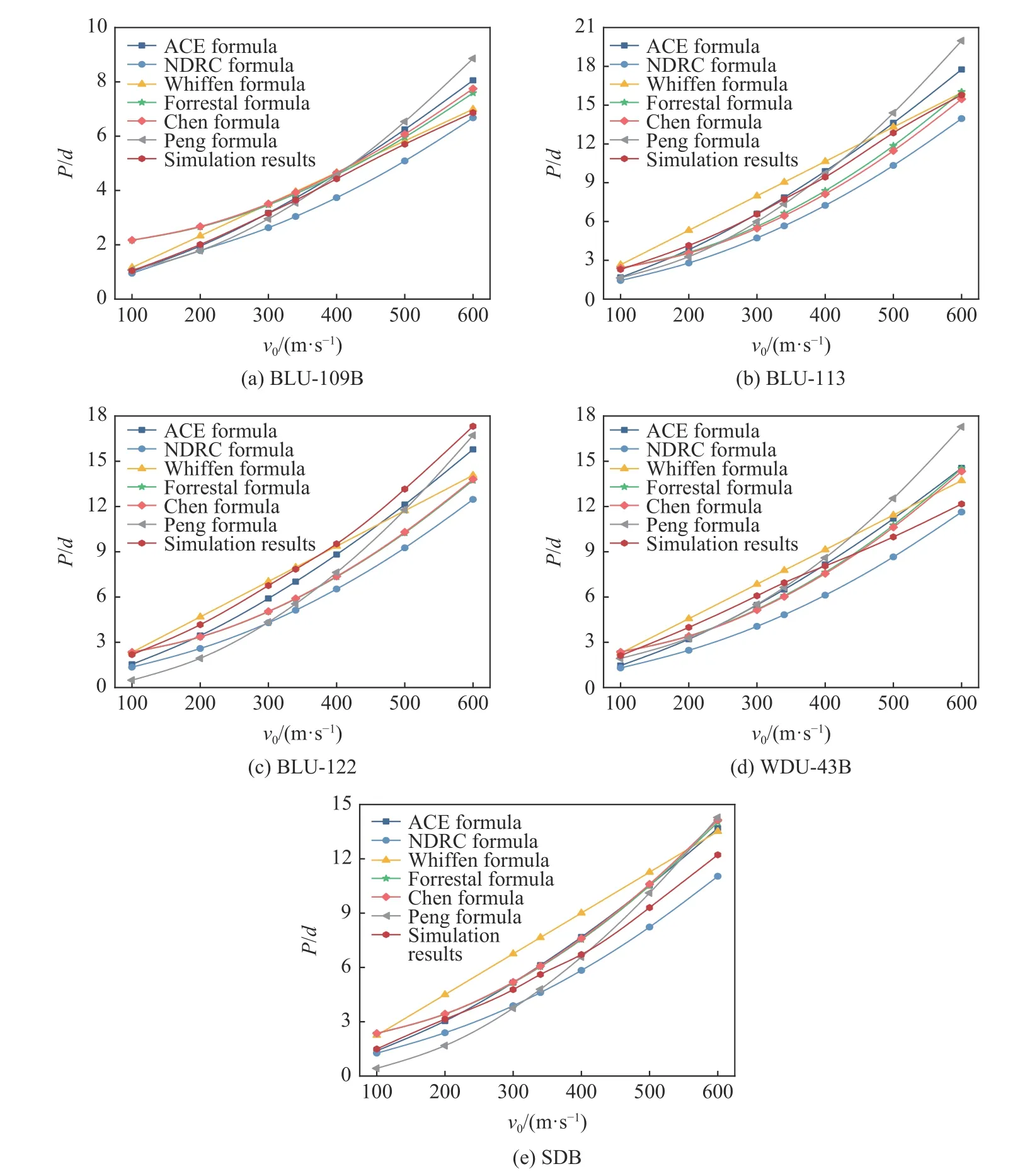
图12 C100 混凝土中5 种战斗部无量纲侵彻深度Fig. 12 Non-dimensional penetration depths of five warheads into C100 concrete
4 钻地弹对不同强度混凝土的侵彻深度
随着工程建设技术与材料科学的交互革新,混凝土材料也得到优化升级和快速发展,高强混凝土在防护结构中的应用愈加广泛。因此,对高强混凝土的抗侵彻性能进行评估显得尤为重要。
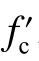

采用由数值模拟方法得到的5 种战斗部在C40 混凝土中侵彻深度(见图11)以及考虑侵彻深度随混凝土强度的衰减规律(见图13),可进一步预测战斗部在不同强度等级混凝土中的侵彻深度。图14 中给出了在所关心的340 m/s 侵彻速度下,采用本文方法预测的5 种战斗部在C40~C200 混凝土中的侵彻深度。同时,鉴于3.1 和3.2 节中ACE 公式均较好地预测了5 种战斗部的侵彻深度,图14 进一步给出了基于ACE 公式中所反映的侵彻深度随混凝土强度衰减规律得到的预测结果。可以看出,随着靶体强度的提高,ACE 公式和本文方法预测结果相近,并且对C100 混凝土侵彻深度的预测结果与数值模拟结果吻合较好,最大误差小于9.0%,验证了图13 衰减规律的可靠性。因此,2 种方法均可用于评估高强混凝土的抗侵彻性能。图11~12 和14 中的预测数据可直接用于确定5 种钻地弹以不同打击速度(100~600 m/s)冲击不同强度混凝土靶体(C40~C200)时的侵彻深度。
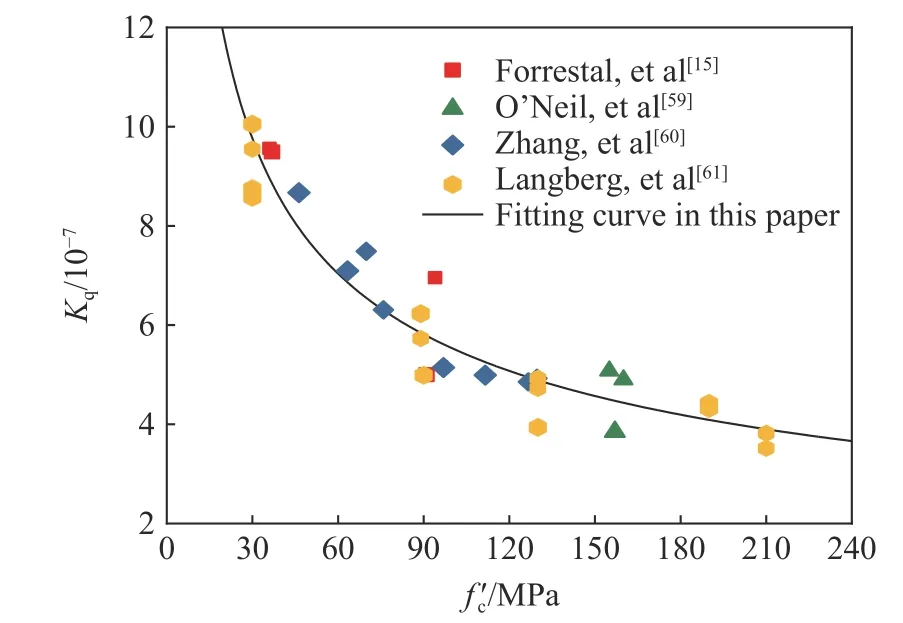
图13 Kq 与之间的关系Fig. 13 Relationship between Kq and
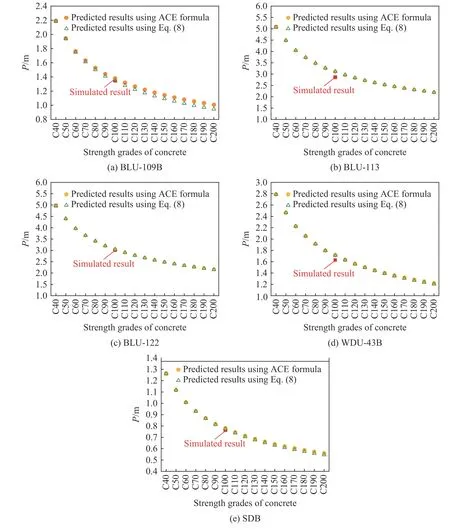
图14 不同混凝土强度等级下5 种战斗部的侵彻深度Fig. 14 Penetration depths of five warheads into the concrete of different strengths
5 总 结
采用试验与数值模拟方法,对美军5 种典型钻地弹侵彻混凝土的深度进行了评估,主要工作及结论如下。
(1)通过对几何相似弹体侵彻相同混凝土靶体试验和数值模拟、几何相似弹体侵彻同比缩放混凝土靶体试验及几何相似弹体侵彻砂浆靶体试验进行分析,确定了引起试验和公式中侵彻深度尺寸效应的主要原因是粗骨料粒径未随弹体尺寸进行同比缩放。
(2)考虑到弹体侵彻深度的尺寸效应,开展了5 发大口径弹体侵彻C40 和C100 混凝土靶体试验和数值模拟分析,提出并验证了大口径弹体侵彻深度的实用化数值模拟方法。
(3) 基于验证的数值模拟算法和本构模型参数,进一步确定了5 种战斗部以不同的打击速度(100~600 m/s)对C40 和C100 混凝土的侵彻深度;通过对7 个经验和半经验公式的适用性进行评估,得出ACE 公式预测精度较高。
(4)基于弹体以相同速度冲击不同强度混凝土靶的试验数据,确定了弹体侵彻深度随靶体强度的衰减规律,进一步得到了音速下5 种战斗部在C40~C200 混凝土中的侵彻深度。
(5) 5 种原型钻地弹以不同速度打击不同强度混凝土的侵彻深度计算结果由图清晰给出,可直接供防护结构设计人员参考。提出的分析方法可推广应用于其余大口径钻地弹侵彻贯穿混凝土靶体分析。
