基于电弧模型的±800 kV直流输电线路带电作业电位转移电流分析

黎鹏， 龙泉， 王申华， 段大刚， 吴田， 普子恒， 方春华

(1.三峡大学电气与新能源学院， 宜昌 443002； 2.湖北省输电线路工程技术研究中心， 宜昌 443002；3.国网浙江省电力公司武义供电公司， 金华 321200； 4.国网湖北省电力公司咸宁供电公司， 咸宁 437100)

为保障超特高压输电线路运行的经济性和稳定性，等电位带电作业作为输电线路消缺的重要手段得到了广泛应用[1-2]。电位转移是等电位带电作业过程的重要环节，指作业人员通过电位转移棒与带电体形成等电位的过程；大量试验表明：电位转移过程中，转移棒和高压导线间会出现拉弧现象，产生高幅值、高能量的脉冲电流，对作业人员的安全造成威胁[3-5]。因此，研究等电位带电作业过程中电位转移电流特性具有重要意义。

目前针对输电线路电位转移电流特性开展了较多研究。文献[3]通过开展1 000 kV耐张塔带电作业电位转移试验，对采集的电位转移电流进行了时频特性分析，得到了等电位过程转移电流的变化规律以及频谱特性。文献[4-5]基于集总电容矩阵理论，计算了不同电压等级下的转移能量，同时仿真得到了转移距离对局部放电电流和电位转移电流的影响。文献[6]构建了基于流体力学理论的电位转移流注放电模型，研究了电位转移过程中电流密度和转移能量变化规律。文献[7-8]对进入±800 kV直流输电线路等电位带电作业电位转移电流进行了实测，建立了暂态响应计算模型，并将转移电流计算值与试验测量结果进行了比较。可见，现有带电作业电位转移电流计算方法未考虑电弧的动态特性，均采用固定电阻模拟转移电弧，且电阻取值主要根据经验选取，可能会影响转移电流计算精度。因此，有必要提出基于实际电弧模型的电位转移电流计算方法，分析电位转移电流的变化规律。

为此，基于控制论电弧模型建立了±800 kV直流输电线路电位转移电流计算模型，分析了电弧参数对电位转移电流的影响，并计算得到了吊篮法和软梯法两种进入等电位方式下的转移电流和电荷量，研究可为作业人员安全防护措施的制定提供参考。

1 基于电弧模型的电位转移电流计算方法

1.1 转移电流理论

对于±800 kV特高压直流输电线路，作业人员手持电位转移棒以吊篮法和软梯法进入等电位过程如图1所示[9-11]。此时，作业人员位于导线和杆塔之间，为悬浮电位状态，即作业人员、导线以及杆塔构成了三导体系统[4]。

研究表明，三导体系统间的空气间隙可等效为集总电容和绝缘电阻的并联[12]，其等效电路如图2所示。进入等电位时，作业人员电位V1由等效电容Cb决定，等电位后作业人员稳态电位V′1由绝缘电阻Ra决定。

(1)

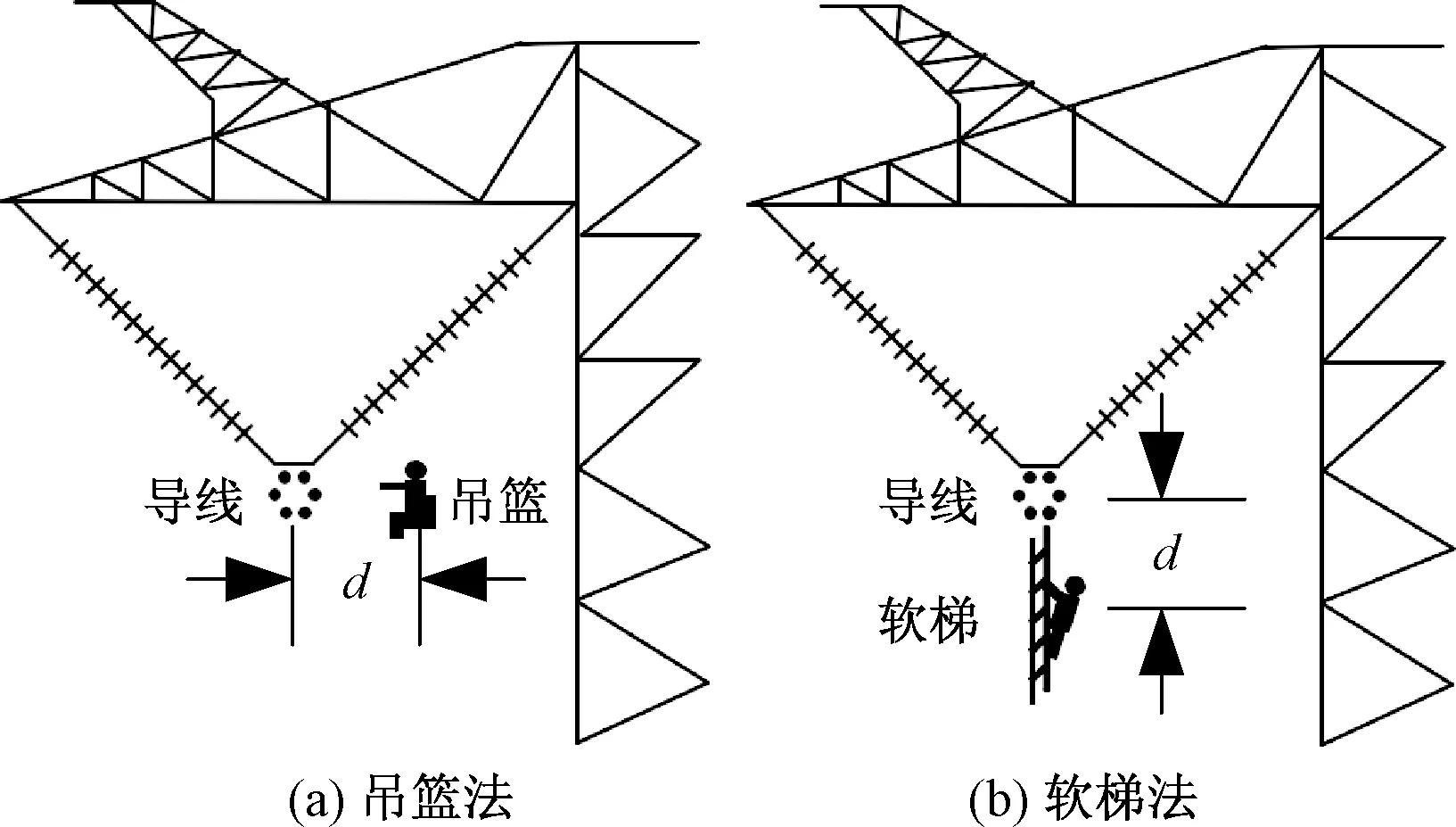
d为作业人员与高压导线之间的距离，即电位转移距离图1 等电位作业方式

式(1)中：U0为线路工作电压800 kV。

作业人员进入等电位过程中，作业人员和导线之间的空气间隙被击穿，电容Ca存储的能量通过电弧-转移棒-人体释放[13]，从而出现暂态电容放电电流-电位转移电流。等效电路如图2所示。

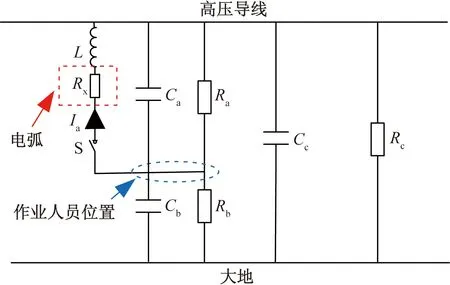
Ca和Ra分别为作业人员与高压导线间的等效电容和绝缘电阻；Cb和Rb分别为作业人员与杆塔、大地及其他导线的等效电容和绝缘电阻；Cc和Rc分别为高压导线与大地的等效电容和绝缘电阻[7]；Ia为电位转移电流；Rx为电弧电阻；L为等效电感，主要与转移棒和导线等有关，一般取值较小，取0.045 mH；通过开关S的动作来模拟作业人员和导线间气隙燃弧和熄弧过程

1.2 电弧模型

常见的黑盒电弧模型包括：Cassie电弧模型、Mayr电弧模型、Schwarz电弧模型、控制论电弧模型[14]。其中，控制论电弧模型考虑了弧长的影响，考虑到带电作业电位转移过程中，电位转移棒逐渐靠近高压导线，转移棒和导线间空气间隙(即电弧长度)逐渐缩小，故选用控制论电弧模型，其表达式为

(2)

式(2)中：i为电弧电流，A；g为电弧电导，S；β为经验系数；Ic为电弧电流的峰值，A；Ec为电弧电压梯度，V/cm；Lc为电弧长度，cm；Gc为稳态电弧电导，即外界条件不变时，维持电弧燃烧的电弧电导值；τc为时间常数，即电流过零后，弧隙中能量变化使得电弧电阻增大到原来e倍(e为自然常数，其值约为2.718)所需的时间[15]。

根据控制论电弧模型理论及式(2)，在PSCAD中搭建的电弧模型如图3所示，通过该电弧模型来描述电弧电阻，从而用于电位转移电流的计算。

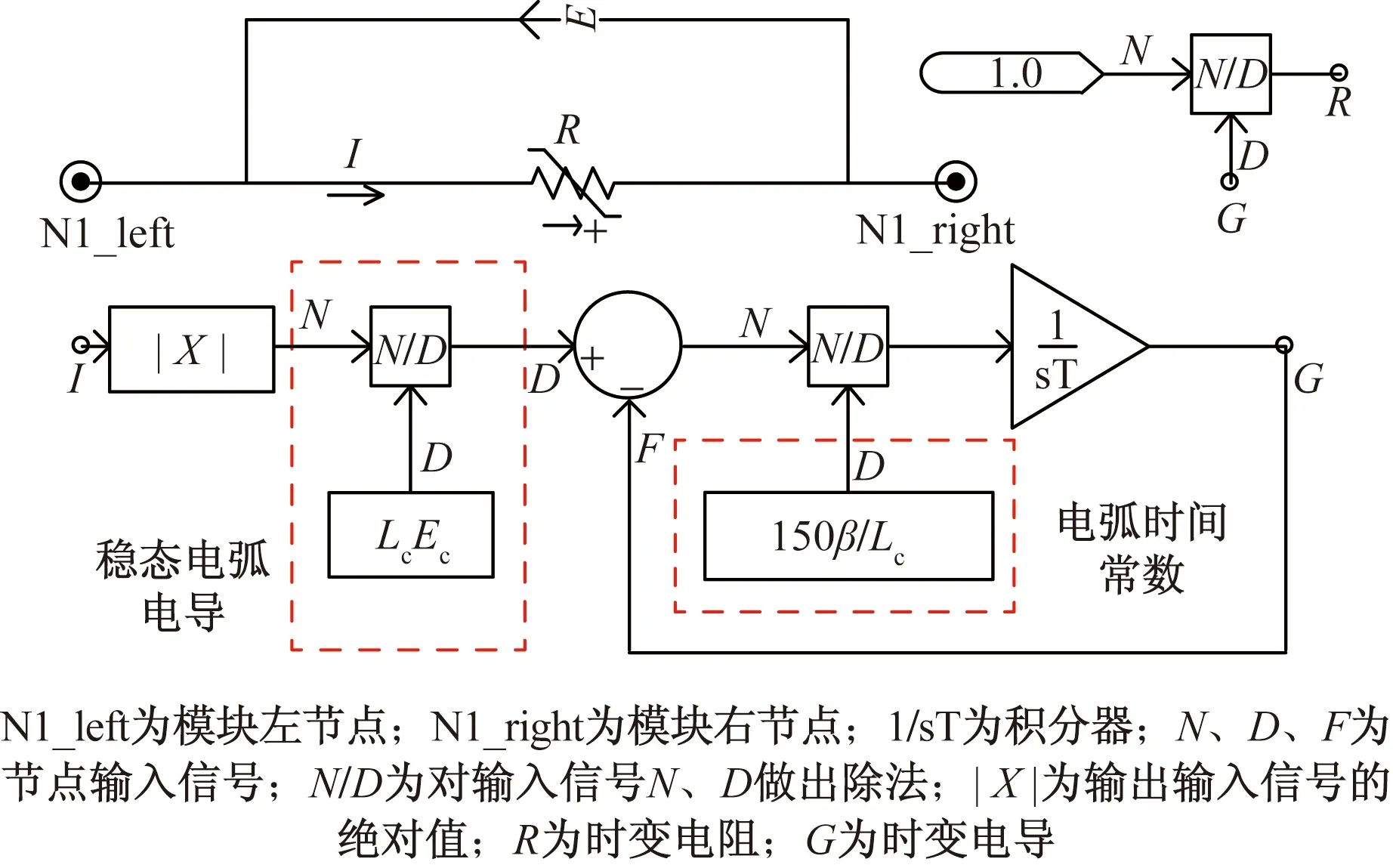
图3 电弧模型

2 电弧模型参数对转移电流的影响

以吊篮法为例(转移距离0.5 m)，分析电弧模型参数对转移电流的影响。根据±800 kV直流输电线路实际结构，并参考相关人体模型尺寸建立仿真模型[7]，通过多导体系统集总电容矩阵计算得出间隙电容参数，绝缘电阻Ra和Rb数值参考文献[4]分别取500 kΩ和2 GΩ，且Ra+Rb≈Rc。

2.1 经验系数β对转移电流的影响

由式(2)可知：β通过改变时间常数τc，进而对电弧特性产生影响。时间常数是电弧热惯性的体现，而弧阻与弧隙温度有关。β越小，τc越小，电流过零后弧阻的上升速率越快，零休时间越短，零休电阻峰值越大。

设定电弧电压梯度Ec=1 kV/cm，弧长Lc=0.3 m，保持其他参数不变，通过改变经验参数β来分析其对电位转移电流的影响。仿真分析发现，当β<3.16×10-10时，电流波形未出现脉冲，即电弧并未形成；当β>1×10-7时，电流波形发生畸变，不能准确描述转移电流的变化，故β的取值范围定为3.16×10-10～1×10-7。β对电弧特性和转移电流峰值的影响如表1所示，可以看出，β增大后，转移电流峰值和零休时刻弧阻逐渐减小，电流峰值时刻弧阻和衰减振荡时间逐渐增大。电弧电压波形如图4所示，随着β增大，过零阶段电弧电压的恢复时间增大、电压下降速度变缓、电压波峰变钝。转移电流波形如图5所示，电流波形均呈正弦衰减振荡变化，但随着β增大，转移电流达峰值时刻和电流过零点时刻延后。当β=3.16×10-10～1×10-8时，转移电流峰值基本不变，维持在154 A。

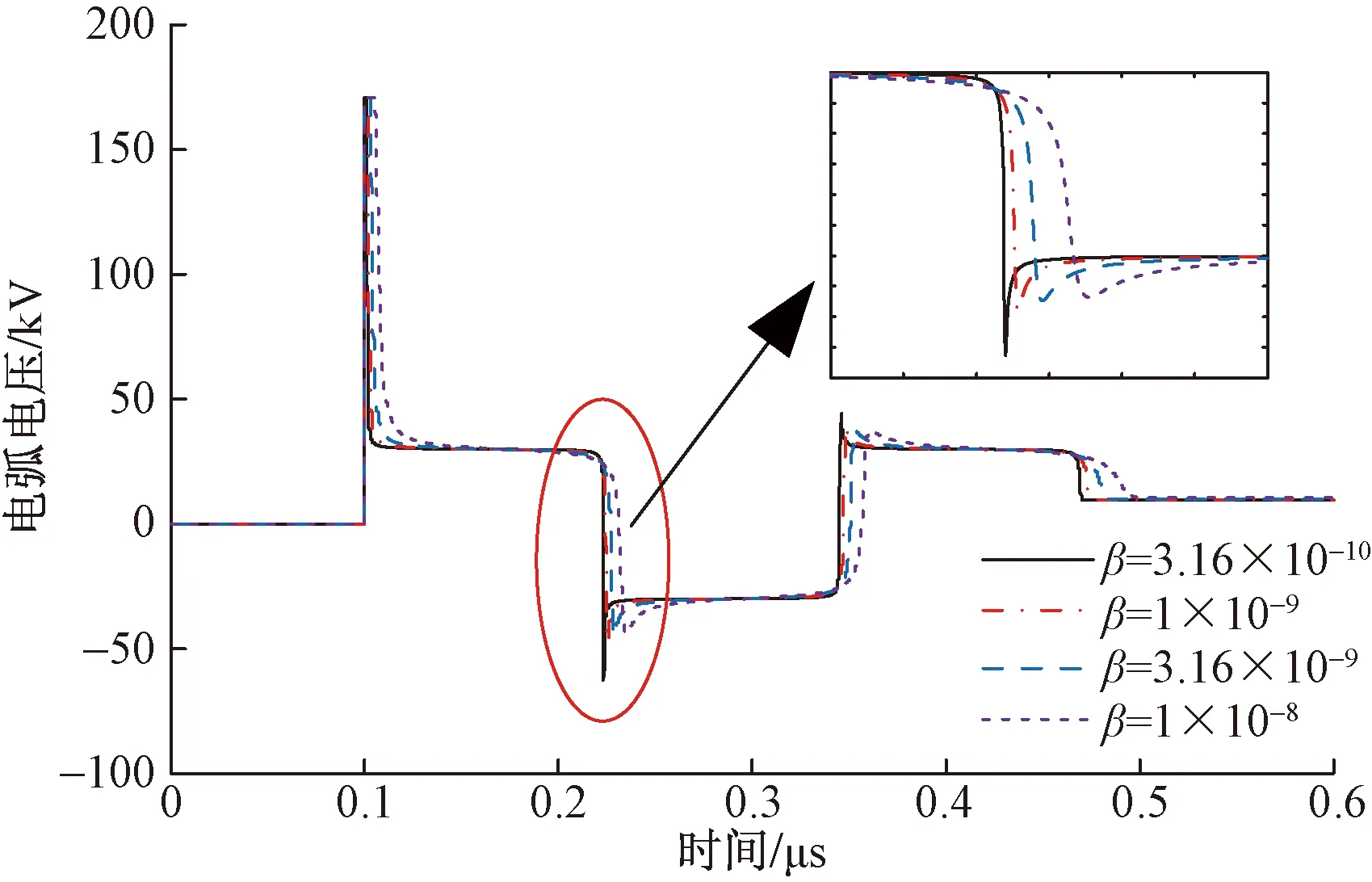
图4 β对电弧电压波形的影响

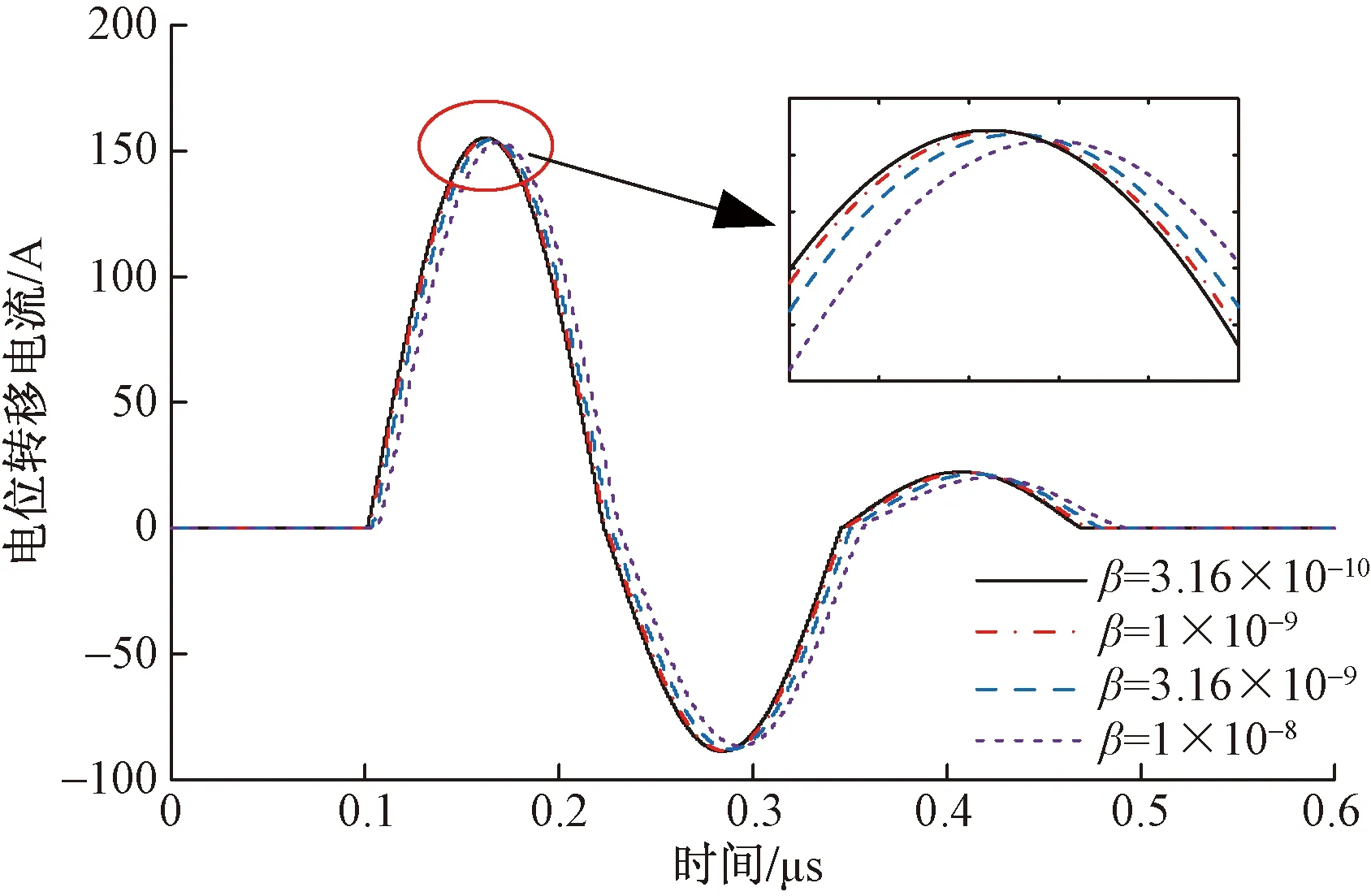
图5 β对转移电流波形的影响

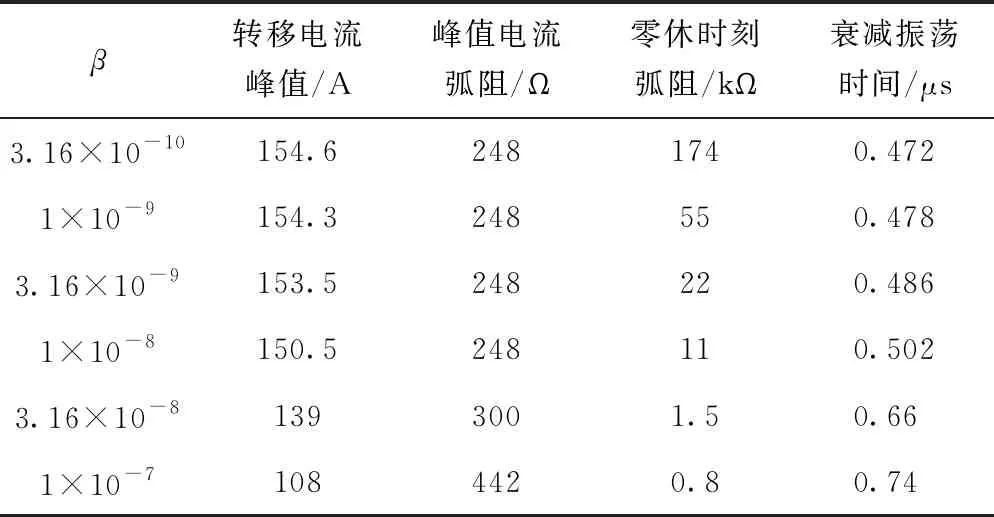
表1 β对电弧特性的影响

2.2 电压梯度Ec对转移电流的影响

由式(2)可知：Ec通过改变稳定电弧电导Gc的值，从而对电弧特性产生影响。Ec越大，弧隙间压降越大，电导Gc越小，稳定燃弧时电阻越大，弧隙释放能量越大。

设定β=1×10-8，Lc=0.3 m，保持其他参数不变，并通过改变Ec来分析其对电位转移电流的影响，具体结果如表2所示。可以看出：当Ec=0.6～1.4 kV/cm时，随着Ec增大，电流峰值时刻的弧阻和零休阶段弧压逐渐增大，转移电流峰值和衰减振荡时间逐渐减小。转移电流波形如图6所示，当Ec增大后，转移电流波形仍然呈正弦衰减振荡，但电流过零点次数变少。当Ec=0.8～1.2 kV/cm时，转移电流峰值维持在154 A左右。

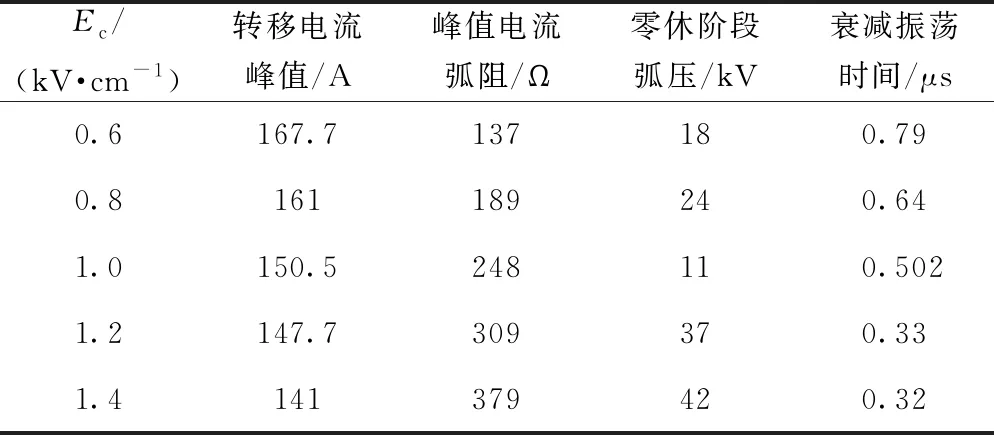
表2 Ec对电弧特性的影响

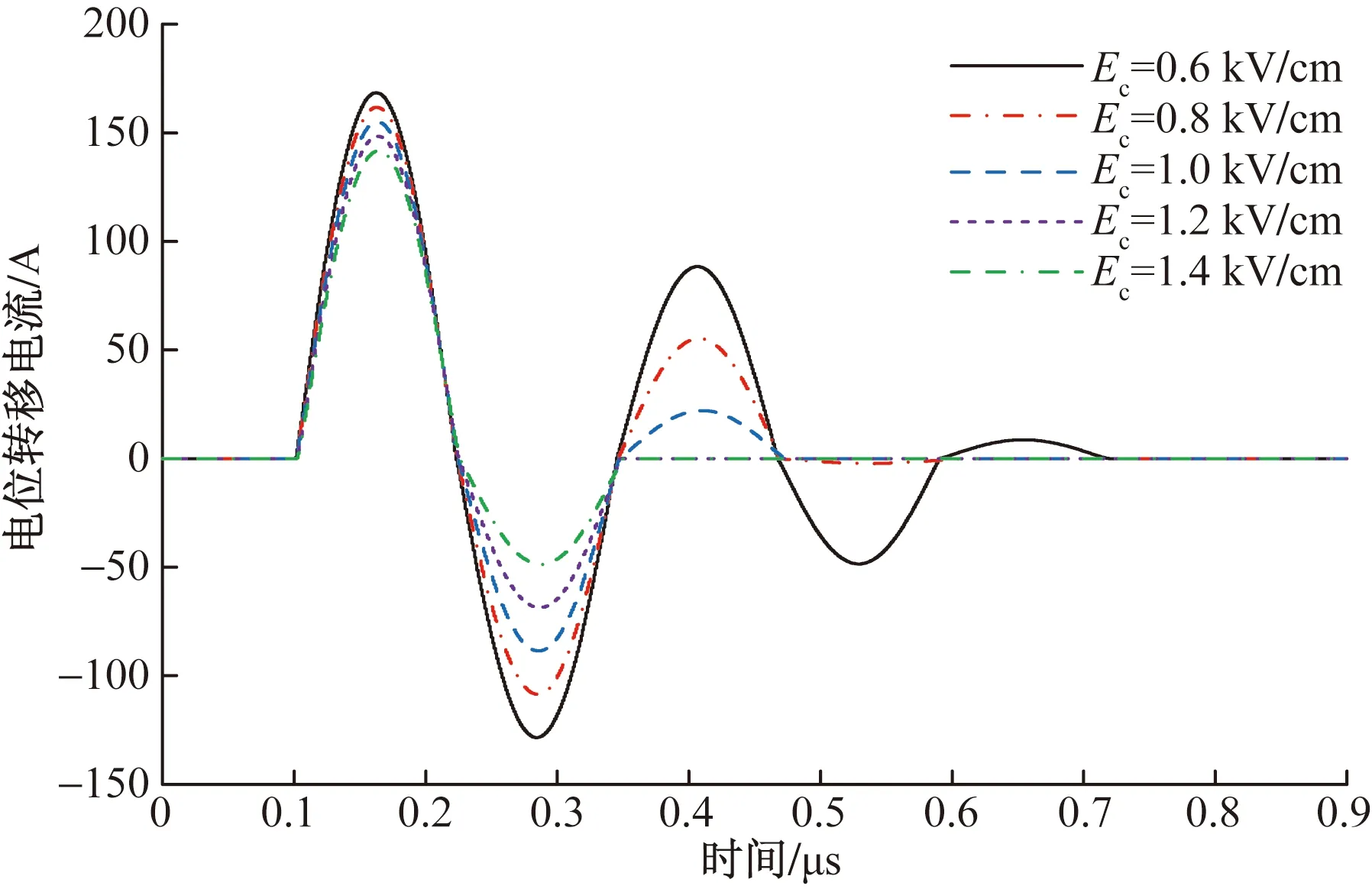
图6 Ec对转移电流波形的影响

由上述仿真可知：经验系数β主要影响零休时刻弧阻，对转移电流峰值影响较小，随着β增大，转移电流峰值时刻延缓，弧压峰值减小，过零阶段电压下降速度减缓。电弧电压梯度Ec主要影响弧阻，进而影响弧压和转移电流峰值，随着Ec增大，转移电流峰值减小，电流过零次数和振荡周期明显减少。故根据进行±800 kV直流输电线路带电作业电位转移电流计算，推荐β取3.16×10-10～1×10-8，Ec取0.8～1.2 kV/cm。

3 不同等电位作业方式电位转移电流计算

基于控制论电弧模型，取β=1×10-8、Ec=1.0 kV/cm，假设Lc固定为0.3 m，仿真分析采用吊篮法或软梯法方式进入等电位时电位转移电流的变化，同时，人体与极导线间转移距离取0.4～0.7 m[16-17]。杆塔型号为ZC27103悬垂直线塔，导线型号为6×LGJ-630/45型钢芯铝绞线，均压环安装在第3、4片绝缘子之间[18]，管径和环径120 mm和2000 mm。建立不同等电位进入方式的模型后，采用ANSYS中的CMATRIX宏命令计算得到三导体系统中对应的集总电容参数[19]。

3.1 吊篮法

作业人员采用吊篮法进入等电位作业的仿真模型如图1(a)所示，计算得到不同转移距离下集总电容的数值如表3所示。

根据表3中的电容参数，计算得到不同转移距离下的转移电流波形如图7所示。电位转移电流均呈衰减振荡，当转移距离增大时，电位转移电流幅值和振荡时间也增大。

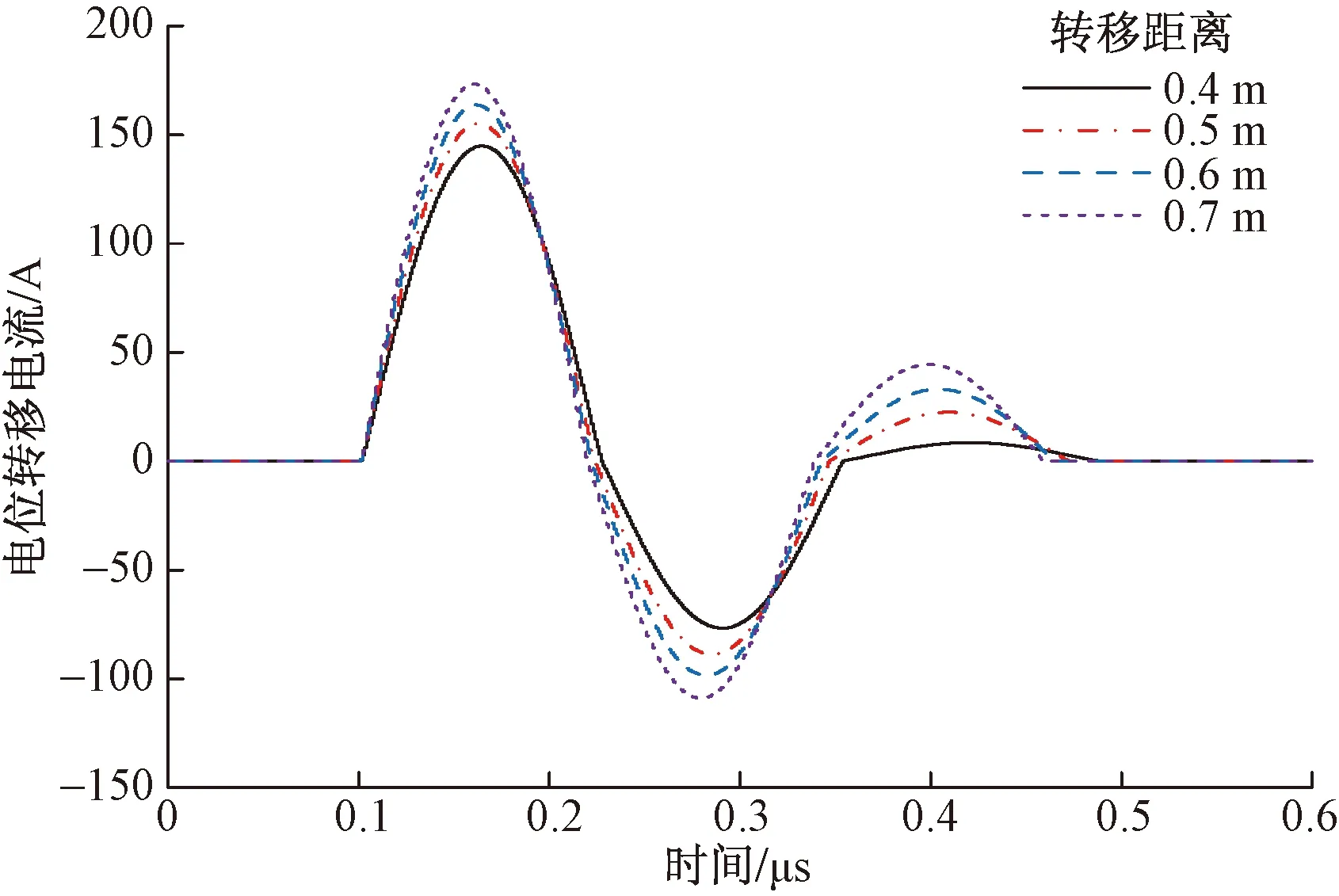
图7 转移电流波形(吊篮法)

表3 集总电容

电位转移过程中，转移电荷量Q可通过式(3)计算，计算得到不同转移距离下，转移电流幅值与转移电荷量的变化规律如图8所示。

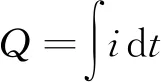
(3)

式(3)中：Q为电位转移过程中释放的电荷量，C；i为电位转移电流瞬时值，A；t为电位转移时间，s。

由图8可知，转移电流峰值和电荷量随着转移距离的增加而增大，当转移距离分别为0.4、0.5、0.6、0.7 m时，转移电流峰值分别为：145、155、164、173 A，对应的电荷量分别为：0.018 3、0.020 7、0.022 6和0.024 6 mC。参考文献[3]中测得转移距离0.5 m时对应的脉冲电流幅值为150 A，仿真计算值为154 A，转移电流峰值计算值与实测值之间的误差小于2.7%，且转移电流变化规律与实测波形规律具有较好的一致性，证明了本文模型的有效性。

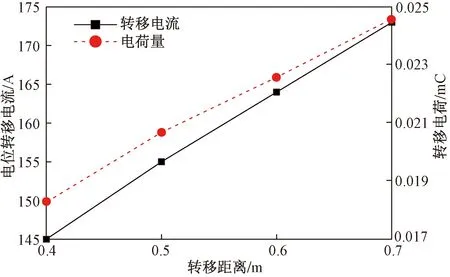
图8 转移电流和电荷量随转移距离的变化规律(吊篮法)

3.2 软梯法

作业人员采用软梯法进入等电位作业的仿真模型如图1(b)所示，计算得到不同转移距离下集总电容的数值如表4所示。

根据表4中的电容参数，计算得到不同转移距离下的转移电流波形如图9所示。当转移距离分别为0.4、0.5、0.6和0.7 m时，转移电流峰值分别为229、239、249和255 A，对应的电荷量分别为0.039 1、0.041 6、0.045 1、0.047 1 mC，其变化曲线如图10所示。不同转移距离下，电位转移电流波形均呈振荡衰减，振荡时间、转移电流峰值和电荷量均随着转移距离的增加而增大。

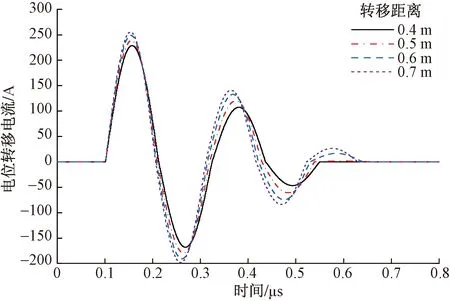
图9 转移电流波形(软梯法)

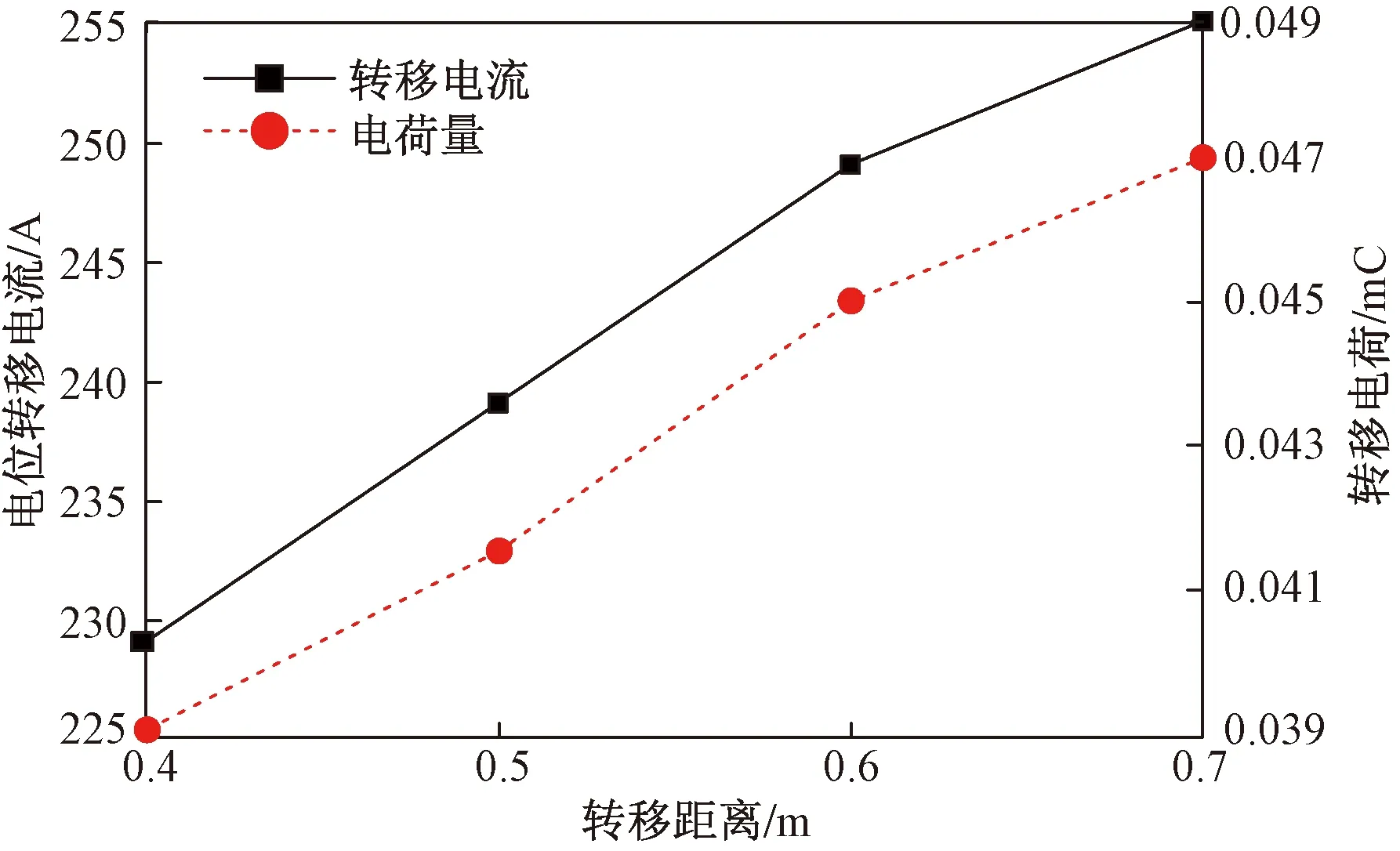
图10 转移电流和电荷量随转移距离的变化规律(软梯法)

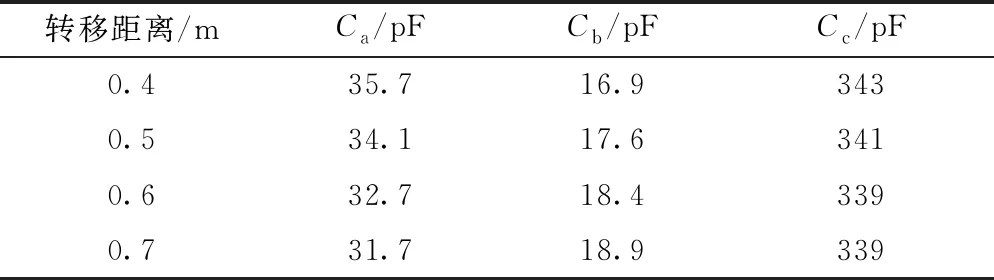
表4 集总电容

对两种进入等电位作业方式进行比较发现：采用吊篮法和软梯法进入等电位时，电位转移电流波形均呈衰减振荡，且转移电流幅值和电荷量均随转移距离增加而增大，但同一转移距离下，使用软梯法时获得的转移电流峰值均大于吊篮法，同时相比吊篮法，软梯法操作更加烦琐耗力，因此，推荐采用吊篮法进入等电位作业。

4 结论

提出了基于控制论电弧模型的电位转移电流计算方法，分析了电弧参数对转移电流的影响，并对不同进入方式下的电位转移电流进行了计算，得出以下结论。

(1)电弧模型中，经验系数β主要影响零休时刻弧阻，对转移电流峰值影响较小，而弧压梯度Ec对转移电流峰值影响较大。

(2)采用吊篮法和软梯法进入等电位时，转移电流峰值及转移电荷量均随转移距离增大而增大；转移距离为0.7 m时，吊篮法和软梯法对应的转移电流峰值分别为173 A和255 A，转移电荷量分别为0.024 6 mC和0.047 1 mC，采用吊篮法时获得的电位转移电流峰值与转移电荷量均较小。

(3)提出了一种基于电弧模型的电位转移电流计算方法，为后续带电作业电位转移电流计算提供了新的思路，但针对进入等电位全过程电位转移电流的计算还需开展进一步研究。