热环境下弹性地基板屈曲路径和振动特性研究

薛治国, 张博, 孙宝印, 王迪

(1.山西路桥第五工程有限公司， 太原 030012； 2.长安大学理学院， 西安 710054；3.河海大学土木与交通学院， 南京 210013； 4.长安大学工程机械学院， 西安 710054)

在环境温度变化较大的地区，道路结构在服役过程中会受到较大的热应力的作用，一方面，会影响道路结构的强度，甚至由于热应力挤压导致屈曲，发生类似于“天然减速带”的横向隆起、甚至断裂的现象[1]；另一方面，热应力以及热屈曲后的热变形对结构的振动特性也会产生复杂影响，给结构的设计带来困难。因此，相关问题的研究至关重要。

根据道路的结构特点，以往学者多将其简化为弹性地基梁、板结构。Winkler地基模型是早期发展起来的简化模型，其将地基简化为相互无关的弹簧，取得了较好的效果[2]。弹性半空间地基模型考虑了基体的连续性[3]。为了弥补上述两种方法的不足，相关学者发展了双参数模型[4]，即在Winkler地基弹簧间引入剪力效应，完善了地基的影响。文献[1,5- 6]分别以不同形式的弹性地基梁、板为对象，基于压杆失稳、薄板失稳等理论，分析了道路隆起的临界温度载荷，揭示了隆起机理，对道路材料的选择、设计和施工方法以及隆起病害的防治提出了建议。

道路所受载荷主要来自于行驶车辆的动载荷。魏纲等[7]分析了Winkler弹性地基板梁的自由振动特征，对其适用范围作了总结。Lü等[8]研究了路面粗糙度对道路结构在移动车辆载荷作用下的响应的影响。Chen等[9]采用虚拟激励法结合精细积分法计算了随机移动载荷作用下Pasternak地基上矩形薄板的振动响应。

结构所处的湿热环境通常会使其内部产生附加应力，甚至使得结构构型发生变化，进而影响其静、动力学行为[10-11]。因此考虑服役环境下，地基板的动力学行为更具现实意义。吴振强等[12]使用有限元方法，研究了壁板结构在热屈曲前后固有频率及振型的演变规律，证实了热环境对壁板结构动力学特性影响很大。李亚杯等[13]使用Rayleigh-Ritz法研究了热效应对圆柱壳结构屈曲和模态的影响规律，发现在屈曲温度附近某些振型将发生跃迁。文献[14-15]分别报道了复合材料层合板和功能梯度板的热后屈曲非线性振动，揭示了热环境对板壳结构的设计具有重要意义。高博等[16]采用近似反演方法推导了黏弹性Winkler地基板温度翘曲应力的计算公式。

综上，相关问题已经有了较多积累，但是对于地基板热屈曲路径以及热屈曲前、后振动特性的研究较少。为此，采用理论方法求解地基板振动控制方程，探究相应的理论分析方法，深入分析了地基板屈曲构型、固有频率和模态形状随温度的演化规律，以期揭示基床系数的影响机理。

1 力学模型

图1为Winkler地基板示意图，处于均匀温升环境中，板长为lx，宽为ly，基床系数为ks，坐标系原点位于板的几何中面。

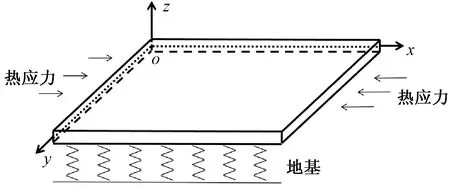
图1 Winkler地基板示意图

根据三阶剪切变形理论，板内任意一点的位移场可表示为[17]

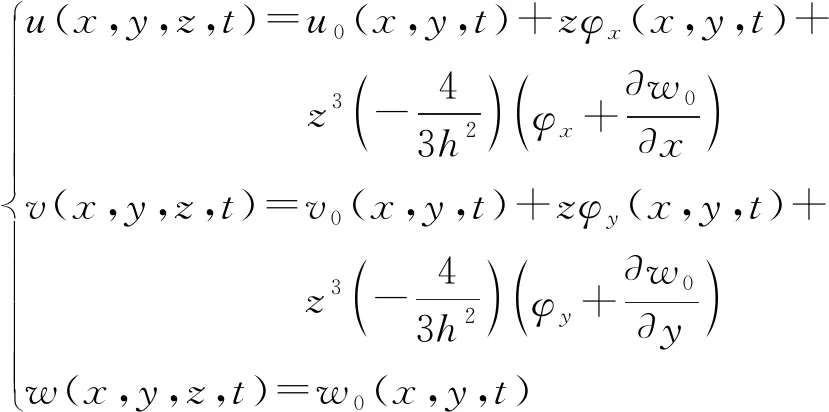
(1)

式(1)中：u、v、w为板中任一点沿x、y、z方向的位移；u0、v0和w0分别为板几何中面上任意一点沿x、y和z方向的位移；φx和φy分别为截面绕y和x轴的转角；h为板的厚度；t为时间。

为了研究地基板后屈曲非线性力学行为，采用von Karman非线性位移-应变关系，则x方向的正应变εxx、y方向的正应变εyy、x-y方向的切应变εxy、y-z方向的切应变γyz和x-z方向的切应变γxz表示为

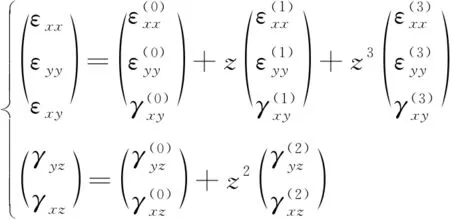
(2)

式(2)中：

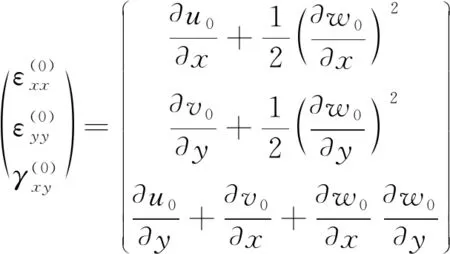
(3)

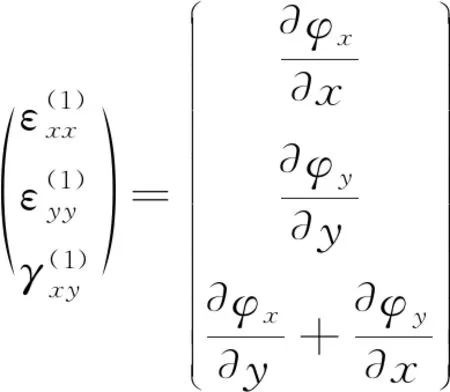
(4)

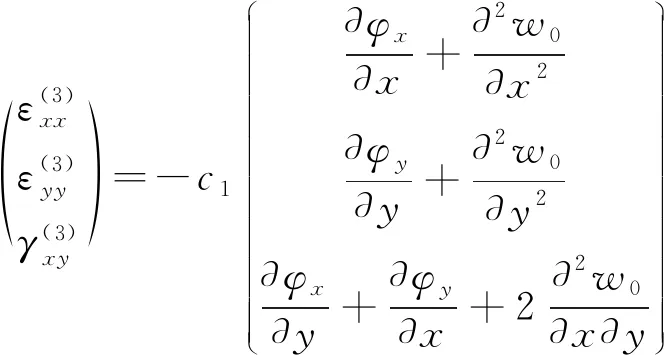
(5)

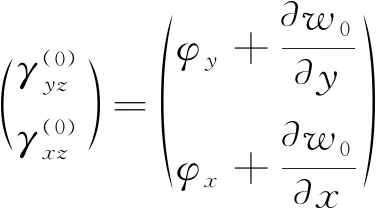
(6)

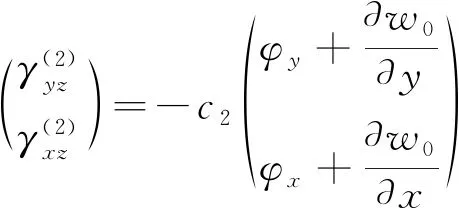
(7)

c2=3c1

(8)

c1=4/3h2

(9)

板为各向同性材料，故本构关系可表示为

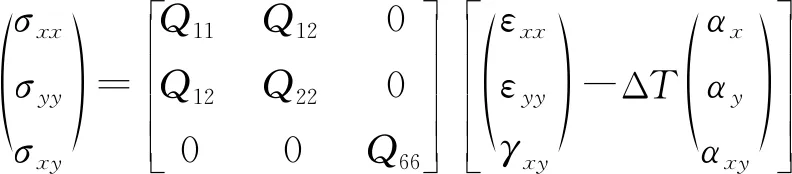
(10)

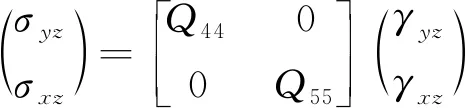
(11)

式中：σxx为x方向的正应力；σyy为y方向的正应力；σxy为x-y方向的切应力；σyz为y-z方向的切应力；σxz为x-z方向的切应力；ΔT为相对于参考环境温度的均匀温度变化值；αx、αy和αxy分别为板沿x、y和x-y方向的热膨胀系数，本研究中为各向同性材料，则可设αx=αy=α，αxy=0，各层的刚度系数Qij可表示为

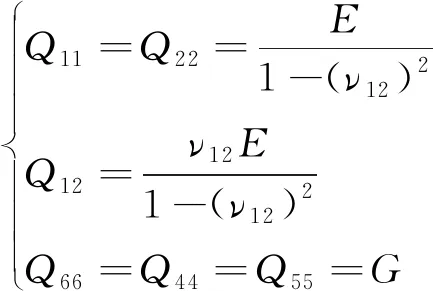
(12)

式(12)中：E为杨氏模量；ν12为泊松比；G为剪切模量。

振动过程中，板的应变能Up可表示为

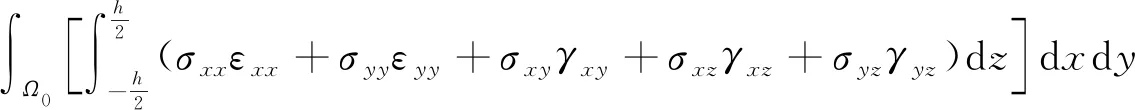
(13)

板的动能Tp可表示为

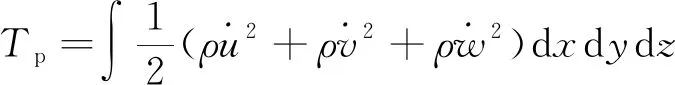
(14)

基于Winkler地基假设，其表面任一点处的位移w(即板在相应点处的横向位移)与作用在该点的应力p成正比，可表示为[18]

p(x,y)=ksw(x,y)

(15)

式(15)中：ks为基床系数。

则振动过程中地基的势能Uks为

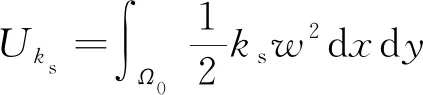
(16)

假设板受横向载荷F(x,y,t)作用，则横向载荷做功Wp为

Wp=∬Fwdxdy

(17)

式(17)中：F为板所受横向载荷。

选取四边简支边界条件[1,7]：

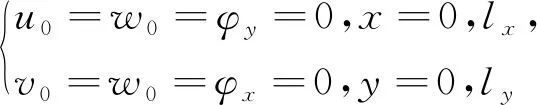
(18)

则根据边界条件，可将位移假设为

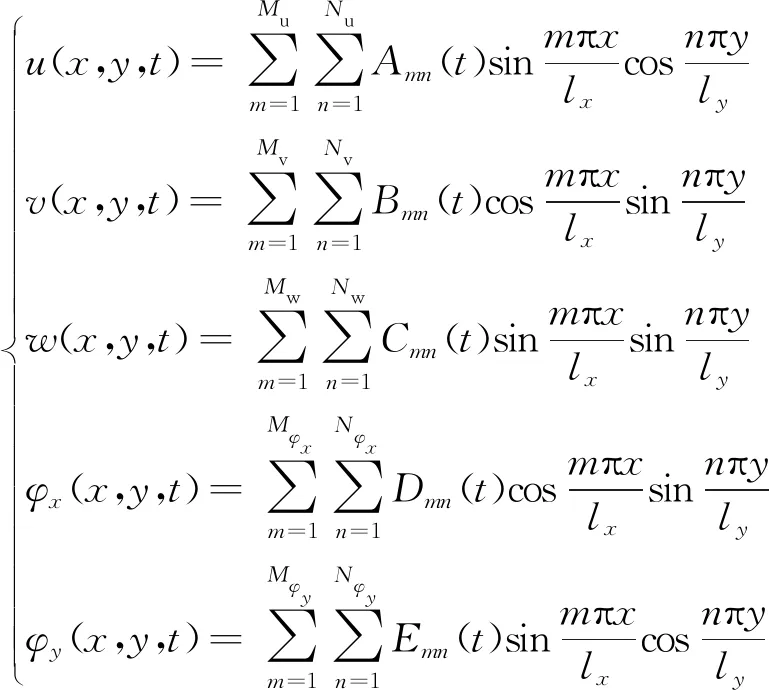
(19)

式(19)中：Mu、Nu、Mv、Nv、Mw、Nw、Mφx、Nφx、Mφy、Nφy为相应位移函数的截断阶数，将式(19)代入式(13)、式(14)、式(16)、式(17)，并引入哈密顿原理：

(20)

则得到考虑温度效应影响的Winkler地基板几何非线性振动控制方程为

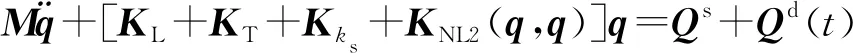
(21)

式(21)中：M为质量矩阵；KL为线性刚度阵；KT由温度效应引起的刚度阵；Kks为由地基带来的刚度阵；KNL2(q,q)为考虑几何非线性所引起的非线性刚度阵；Qs为由温度引起的静态横向载荷列阵；Qd(t)为由横向外部动态载荷引起的动态载荷列阵；q为由式(11)中广义位移组成的广义位移列阵。

为了得到在稳态热载作用下板屈曲前后静力平衡位置处的振动特性，首先将广义位移表示为热载作用下的静态广义位移qs和动态载荷作用下以静态平衡位移为参考位置的动态广义位移qd(t)之和。

q(t)=qs+qd(t)

(22)

则可将式(21)写为温度载荷作用下的非线性静力方程为

[KL+KT+Kks+KNL2(qs,qs)]qs=Qs

(23)

以非线性静力位移为参考位置的线性振动方程为

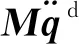
(24)

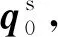
2 实例分析

以一典型地基板结构为对象，对不同基床系数下热后屈曲路径、屈曲前后固有频率和模态进行计算，得到地基板屈曲变形特征和固有特性的演化规律，揭示地基的影响机理。板的长为2.5 m，宽为1.5 m，厚为0.02 m，材料属性如表1所示。

表1 材料属性

2.1 结果验证

取假设位移截断阶数均为5，即Mw=Nw=5,Mu=Nu=5,Mv=Nv=5,Mφx=Nφx=5,Mφy=Nφy=5。基床系数为2×106N/m3，处于常温环境中。如表 2所示，将理论结果与利用Ansys计算的有限元结果进行对比，发现理论结果与有限元计算结果对比一致，故在接下来的分析中均以此作为截断阶数。

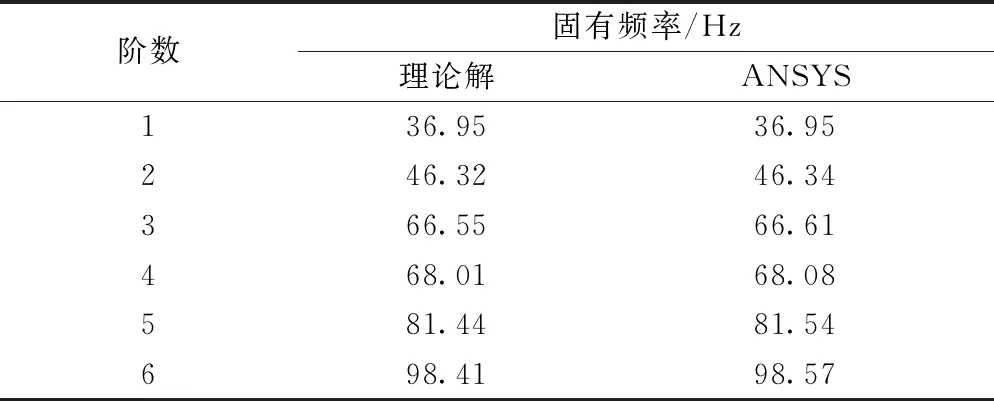
表2 固有频率对比验证

2.2 不同基床系数下地基板的热屈曲路径

图2为不同基床系数下地基板屈曲温度的变化趋势，可以看出，随着温度的升高，地基板的屈曲温度也随之升高。地基的存在使得板产生了附加刚度，基床系数越大，地基对板的刚化效应越明显，进而使得地基板的屈曲温度不断升高。

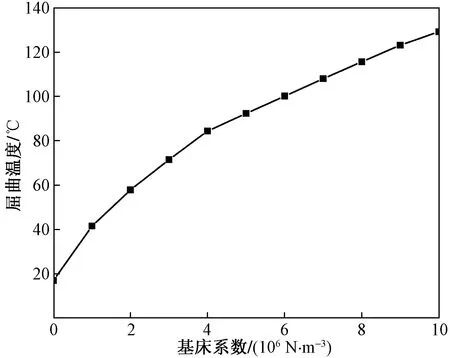
图2 不同基床系数下地基板的屈曲温度

所研究的地基板是关于板中面几何对称的均质材料板，且温度均匀分布，故在屈曲前，板不产生横向位移，而在屈曲后，地基板失去了稳定性，微小的横向扰动即可使地基板从初始时刻的不稳定位置进入新的稳定位置，即发生了屈曲变形。为了研究基床系数对地基板屈曲路径的影响，选取了基床系数分别为0、1×106、2×106、5×106N/m3的4种情况，对地基板的屈曲路径和屈曲变形进行了计算分析。图 3为4种基床系数下，地基板1/4点(0.062 5、0.037 5 m)处的屈曲位移随温度的变化曲线。可以看出，4种基床系数下，在屈曲后，位移均随温度的升高而不断升高，同时，由于结构和温度场的对称性，在屈曲点处位移发生分叉，出现了关于几何中面对称而幅值相等的两条屈曲路径，而实际沿着哪一条路径发生屈曲，取决于横向扰动的方向。从图3还可以看出，与图2一致，基床系数的提高使得地基板的屈曲温度明显提高，即地基的增强可以抑制地基板的屈曲。

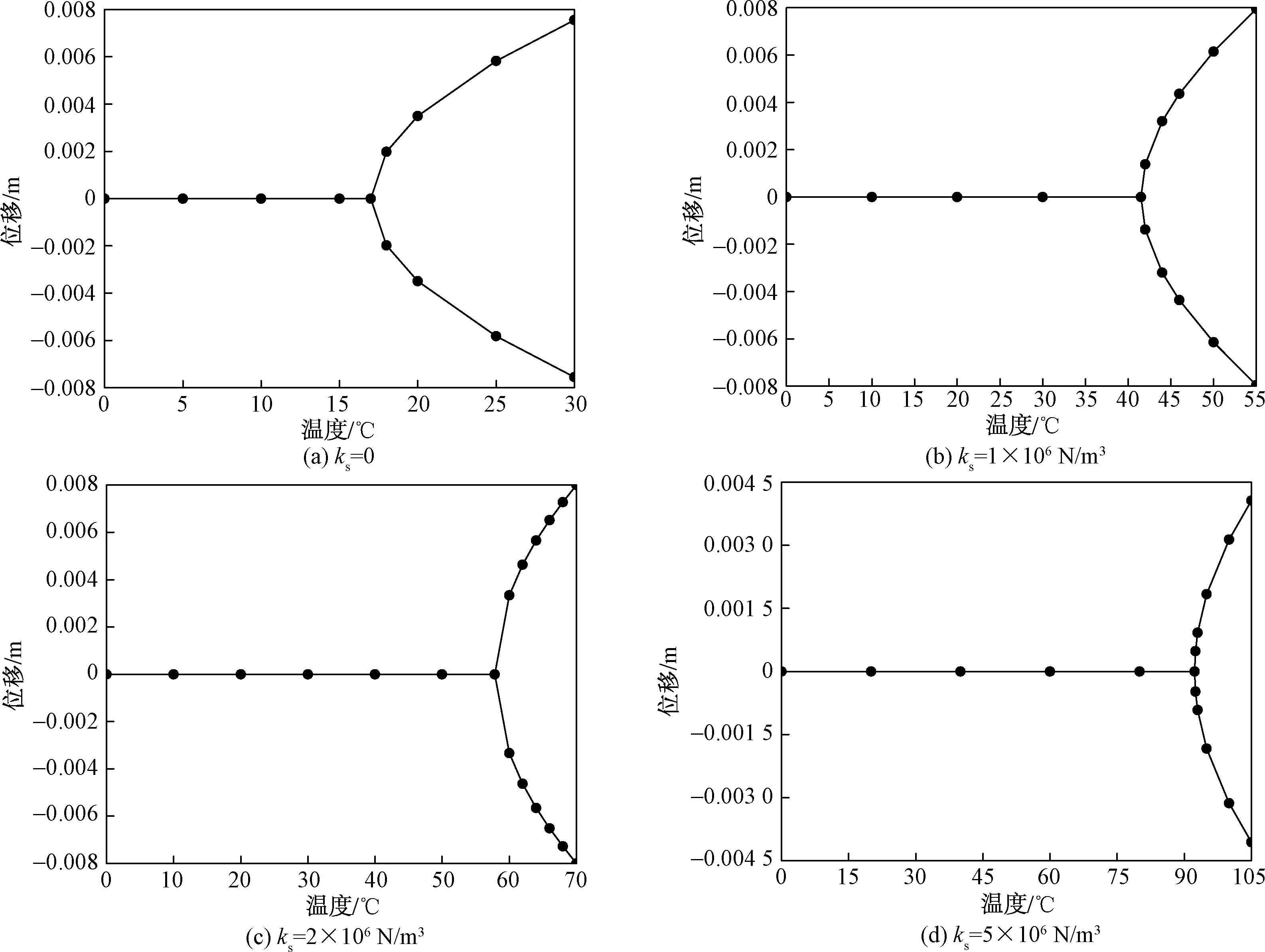
图3 不同基床系数下地基板1/4点(0.062 5 m，0.037 5 m)的屈曲路径

在屈曲路径分析的基础上，计算并绘制了4种基床系数下，不同屈曲温度点处地基板的屈曲构型，结果展示在图4中。可以看出，在每一种基床系数下，热屈曲后，随着温度的升高，地基板的屈曲变形形式基本保持不变，只是幅值随着温度的升高而不断增大。值得注意的是，不同基床系数下，地基板的屈曲构型差异较大，随着温度的升高，地基板各阶模态顺序发生交换，而不同基床系数下，在屈曲温度附近的第一阶模态形状均与图4中的屈曲构型形状保持一致，故可以得出，地基板的屈曲构型形状，与屈曲温度附近的第一阶模态形状直接相关。

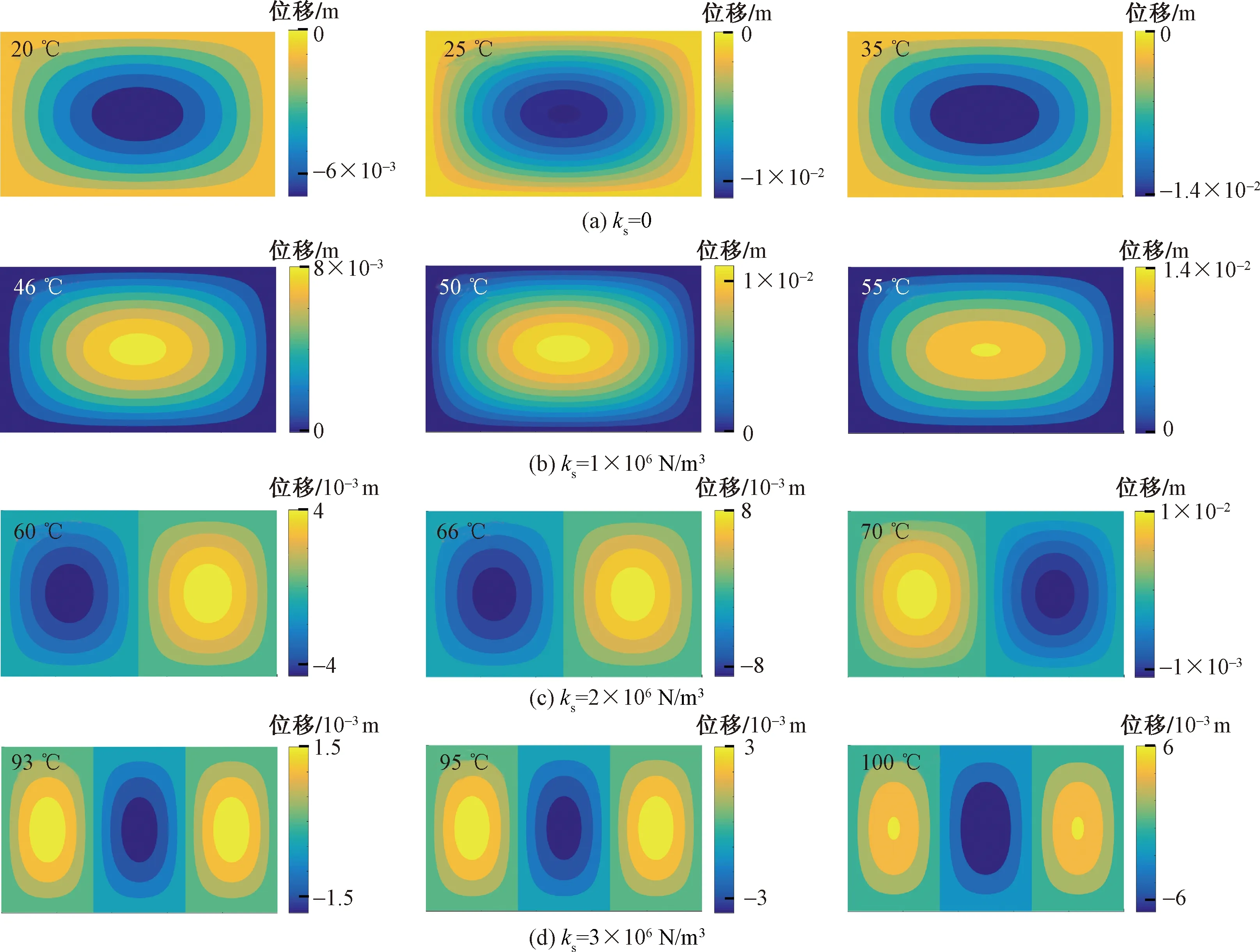
图4 不同基床系数下地基板不同屈曲温度下的屈曲构型

2.3 不同基床系数下地基板的热屈曲前、后固有特性演化规律

在屈曲路径分析的基础上，进一步计算得到了屈曲前、后不同温度下地基板的固有频率和模态形状。图5为基床系数分别为0、1×106、2×106、5×106N/m3时固有频率随温度的演化规律，结合2.2节关于屈曲温度的计算结果可以发现，在屈曲温度之前，随着温度的升高，地基板内的热应力逐渐增大，而热应力是压应力，对板的刚度起到软化效果，故频率逐渐降低，并在屈曲温度点处第一阶固有频率降至零点，随后，地基板不再是平板，而是产生如图4所示的屈曲构型，而屈曲构型的出现则会增大地基板的刚度，使得固有频率在屈曲温度之后开始上升。热应力的软化效应与热屈曲构型的刚化效应对各阶固有频率的影响大小不一样，使得频率间发生顺序交换，相应地，图6所示的相应阶模态顺序也发生了交换。对比发现，地基的存在使得地基板固有频率整体提高，且基床系数越大，各阶固有频率越聚集，模态间顺序发生交换的情况越多。图6(a)、图6(b)中，基床系数为0和1×106N/m3时，各阶模态顺序随着温度的升高保持不变，其一阶模态形状与图4(a)和图4(b)中屈曲构型形状一致；图6(c)中，基床系数为2×106N/m3时，相较于常温下，在屈曲温度(50 ℃)附近，一二阶模态顺序发生了交换，故图4(c)中的屈曲构型形状与其常温时的二阶模态形状一致；图6(d)中，基床系数为5×106N/m3时，模态交换更为复杂，在屈曲温度(92 ℃)附近，常温下的第三阶模态变成了第一阶模态，其与图4(d)中的屈曲构型形状一致。

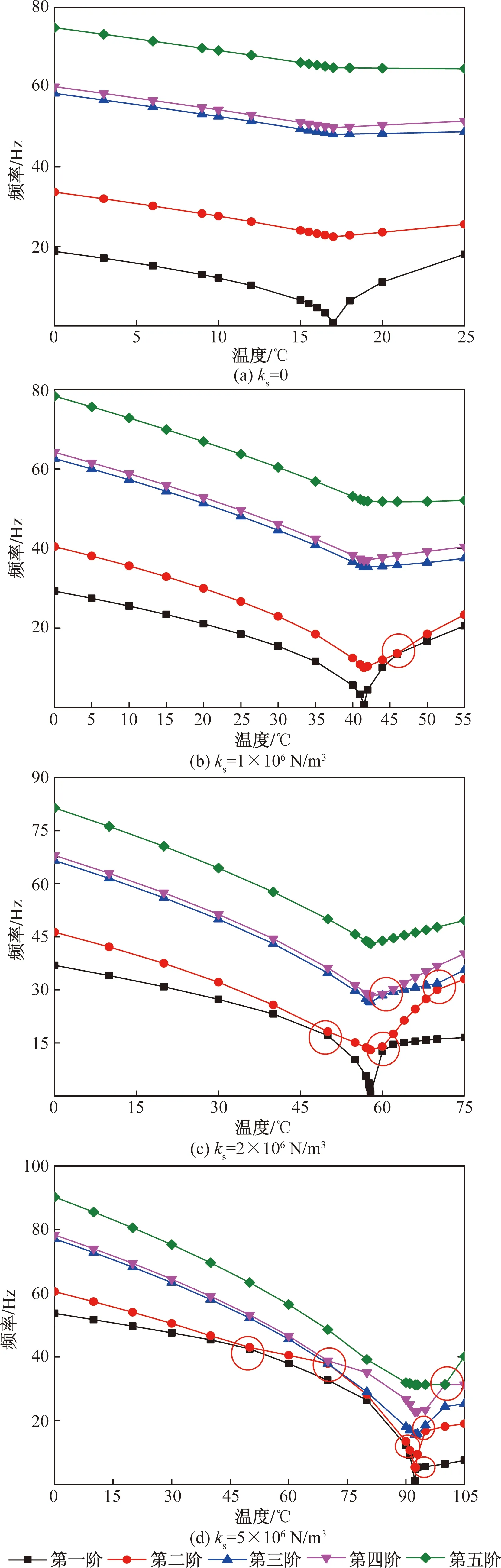
红色圆圈标记出的是频率曲线相交的点

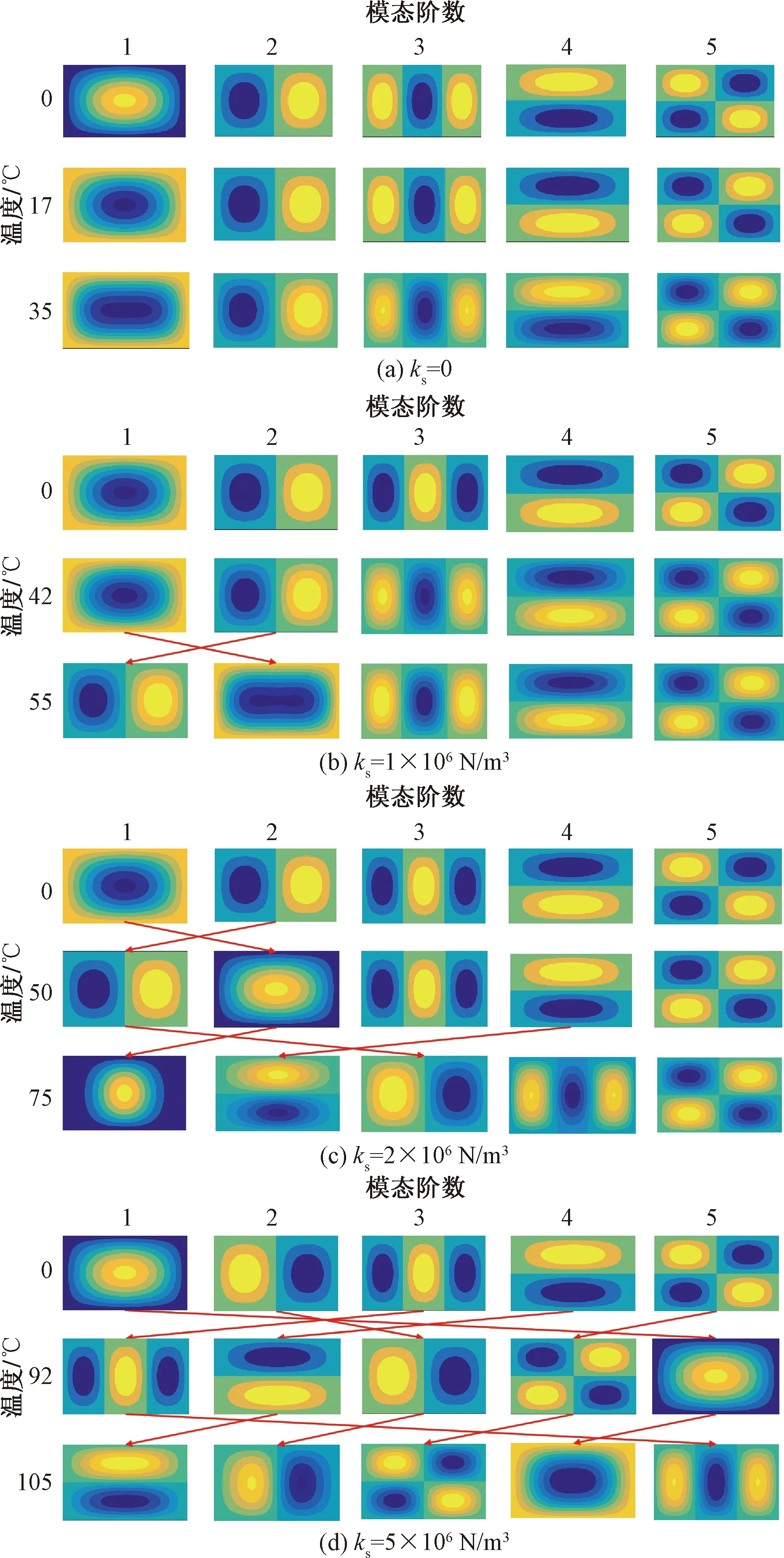
图6 不同基床系数下地基板热屈曲前、后模态形状演化规律

3 结论

以Winkler地基板为对象，考虑热应力效应，理论推导了其非线性振动控制方程，发展了两步分析方法。得出如下结论。

(1)基床系数越大，地基板的屈曲温度就越高，同时，地基板的屈曲构型形状也会发生较大变化，通过与模态形状的对比显示，屈曲构型形状与地基板在屈曲温度附近的第一阶模态形状一致。

(2)屈曲前，热应力对地基板有软化作用，各阶固有频率不断降低，基频在屈曲点降至零点，而后由于屈曲构型的产生，对地基板产生刚化效应，固有频率开始升高，由于热应力和热变形对各阶固有频率和模态的影响大小的不同，会发生频率和模态顺序发生交换的现象，且基床系数越大，交换现象越频繁。