基于管沟尺寸的冻胀作用下输油管道应力分析

王健， 顾晓婷*， 张瑶瑶， 杨燕华

(1.长江大学石油工程学院， 武汉 430100； 2.油气钻采工程湖北省重点实验室， 武汉 430100；3.新奥天然气股份有限公司， 廊坊 065000)

中俄原油管道穿越中国多年冻土区和季节冻土区，冻土地区活动层易受温度影响导致土体冻结发生冻胀现象。管道敷设在冻土中受土壤活动影响较大，土体会因水热现象形成冰锥、冻胀丘等，进而影响管道的受力变形。由于管道需要敷设在管沟中，管沟开挖和冻土回填时管道周围土体密度不均造成管沟积水[1]，再经冻融循环后，管道局部会出现应力集中现象导致屈服弯曲。

Wu等[2]利用有限元数值模拟，研究了由冻胀丘引起的管道受力变形及应力分布。Wen等[3]建立弹塑性有限元模型，分析管道在穿越冻土区时管道随冻胀作用的最大变形及受力。王国丽等[4]论述了基于应变设计方法下的管道因冻胀融沉引起的变形计算方法，并进行了实例分析。王洪波等[5]以简化的冻胀模型分析了输气管道与土体的相互作用，为输气管道在冻土中的设计提供了相关理论。黄龙等[6]基于弹性地基梁，利用有限元模型分析了地基特性参数与温度的关系，研究了管道在不同地基参数下的应力变化。狄彦等[7]提出了冻土冻胀对管道的计算方法和模型以及管道基于应变的失效判据。李超营等[8]研究了冻土区不同斜坡角度对埋地管道的影响，分析了斜坡角度和融沉长度对管道应力变化。张旭等[9]利用非线性数值模拟方法研究漠大线管道的应变影响规律，分析得出管道壁厚对管道受力变形影响最大。上述研究虽论述了管道及冻胀区土壤参数与管道应力应变的关系，但未考虑管道周围冻土实际温度场，只施加冻胀载荷进行模拟分析，未能分析土壤温度变化对管道应力的影响且均未提及管沟参数。而实际上，根据《输油管道设计规范》(GB 50253—2014)[10]，管道敷设时需进行管沟开挖、土壤换填和回填，由于管沟换填土质类型及含冰量等的不同，冻胀量也会有差异。尤其是在过渡区与冻胀稳定区，会引起管道的弯曲变形，管沟参数对管道应力应变的影响更直接、经济有效。

为使有限元分析结果更符合管道敷设在一定管沟尺寸下的实际要求，针对输油管道利用ABAQUS有限元软件，基于耦合场的分析方法，考虑钢质管道材料的非线性特性和土壤材料随温度变化的非线性特性，管道内壁承受油温及压力载荷，外壁承受非线性热应力以及经由大气、土壤、管道之间传热所获的温度载荷。根据中俄原油管道工程漠大线冻土工况，确定计算区域和边界条件，对管道周围土体温度场及应力场进行耦合分析，建立了含管沟参数的热固耦合模型。研究土壤温度变化、管沟边坡坡度，沟底加宽裕量等对管道应力的影响规律，揭示了影响管道安全性的关键因素，旨在为今后冻土区埋地管道设计提供理论基础。

1 应力模型

土体在冻结发生后依然会有未冻结的薄膜水，这时低温吸力的增加和渗透率的降低会导致晶体的析出和冰透镜的形成并侵入土体[11]，土壤体积增大引起地面膨胀。冻土物理学性质会随温度而变化，冻土与大气间的热量平衡状态会被输油管道破坏，导致管道翘曲变形。输油管道在冻土区运行时，除受重力外，由于土壤温度的变化还会受到管道周围土壤的约束与压迫而产生的应力。

1.1 温度场控制方程

冻土区埋地管道周围温度场分布随时间变化而变化，其会受到管道油温与土壤温度的共同影响，温度场的热量平衡控制微分方程如下。

(1)在冻结区。

(1)

(2)在融化区。

(2)

(3)管壁。

(3)

式中：ρf、ρu、ρi分别为冻结区土壤、融化区土壤、管壁的密度；Cf、Cu、Ci分别为冻结区土壤、融化区土壤、管壁的热容；λf、λu、λi分别为冻结区土壤、融化区土壤、管壁的导热系数；Tf、Tu、Ti分别为冻结区土壤、融化区土壤、管壁的温度；t为时间；r、θ为坐标。

(4)热固耦合方程为

(4)

(5)

式中：σx、σy为正应力，MPa;τyx、τxy为切应力，MPa；fx、fy为体力分量，MPa；x、y为坐标方向。

假设初始时刻管道的温度为Tg0,当升温至Tg时，管道会因为温度的变化发生膨胀而产生应变变化，其计算公式为

εhot=-β(Tg-Tg0)

(6)

式(6)中：εhot为管线膨胀产生的热应变；Tg为管道温度，℃；β为管道的线膨胀系数。

1.2 定解条件

初始条件:设Tw为地面温度；Ta为地面温度；T0为土壤初始温度；距地面H深度的土壤温度为TH，则大气与土壤表面的对流边界条件为

T|y=H=T0

(7)

(8)

式中：T为地面温度，℃；λ为土壤导热系数；α为土壤线膨胀系数；h为土壤与大气间的对流换热系数。

2 模型建立

2.1 管道基础参数

建立X60管道模型，管道直径813 mm,壁厚12.7 mm，密度7 800 kg/m3,埋深1.8 m(地表到管顶)屈服强度415 MPa，其他参数如表1所示。管线钢材料特性由真实应力-应变关系来模拟，为了真实描述其塑性变形，由单向拉伸试验的名义应力-应变转换为真实应力-应变，曲线如图1[12]所示。

表1 管线钢参数

图1 X60管线钢真实应力-应变曲线[11]

2.2 土壤基础参数

冻土区土壤与普通土壤不同之处在于冻土区的土壤对温度具有较高的敏感性，土壤的温度会影响其弹性模量及泊松比。水分冻结成冰引起的体积膨胀是冻胀的主要原因[13]，冻土的冻胀量可以由土壤的线膨胀系数来确定，粉质黏土与砂土的含水率为29.82%、12%，根据式(9)可得冻结土壤的线膨胀系数α1=-0.000 375、α2=-0.000 138[14]。

(9)

式(9)中：α为土壤线膨胀系数；ΔT为温度变化量，℃；ω为土壤含水率。

土体冻融的导热系数和比热会由较大变化，热参数的变化可以由不同温度下的焓值来定义。焓与温度的对应关系如式(10)所示,焓值单位：J/m3。管沟内土壤用砂土换填，土壤参数如表2[15]所示。

表2 回填砂土土壤参数[15]

(10)

对时间进行微分得

(11)

再将式(1)代入式(11)得

(12)

式中：H(T)为土壤焓值；ρ为土壤密度；c(T)为比热容；λ(T)为热传导系数。

2.3 有限元模型

利用ABAQUS软件建立含管沟的穿越冻土区输油管道三维管土模型，利用Drucker-Prager弹塑性本构模型模拟土壤，管沟剖面如图2所示，管沟边坡坡度根据土壤及其物理学性质确定，包括土壤黏聚力，密度等。管沟沟底宽度为加宽裕量和管道直径之和，加宽裕量一般不小于0.5 m。3D模型采用8节点缩减积分C3D8R热固耦合六面体单元对管道及土壤模型进行结构离散，每个节点具有一个温度自由度，网格互不重叠。考虑到管道周围温度梯度大离散过程中对管道及管沟土壤区域进行网格加密，在管道壁厚方向划分单元层数，远离管道及管沟的土壤网格划分较粗略。管土模型最终的网格划分方案网格单元数为28 522，节点数43 578。管-土间的相互作用由接触面法定义，允许管道表面与土体表面发生接触与分离，属于有限滑动接触，摩擦系数为0.3。模型上边界地表与大气会以对流传热的方式进行热交换，对土壤表面施加对流换热系数模拟真实情况，对流换热系数取17.8 W/m2·K[16]。管道与周围土壤为面-面接触，热交换形式主要为热传导，模型左右边界距离管道足够远，且管道水平方向的温度传播有限，因此将模型两侧设置为绝热边界。天然地表下地温年变化深度以下的土壤温度梯度且超出了输油管道热传导范围，认为计算区域的下边界为恒温。管土作用模型如图3所示。

K为加宽裕量，mm；D为管道外径，mm；A为管沟坡度；α为管沟坡度角，(°)

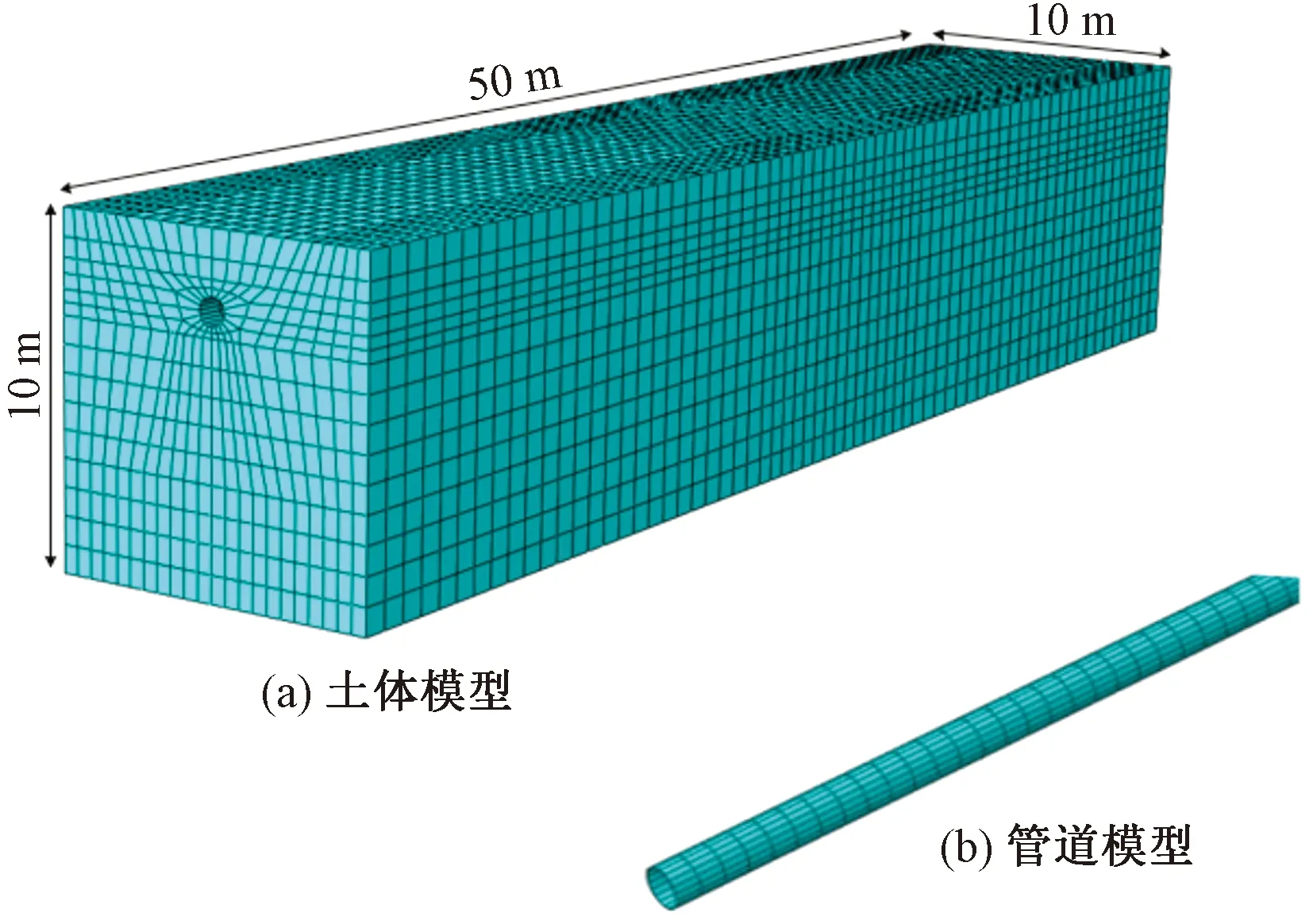
图3 管土相互作用模型轴向方向

2.4 模型验证

中俄原油管线漠河-大庆段输油工程穿越中国东北大兴安岭，该区域冻土类型较多，冻土层厚度平均在2～5 m，土壤岩性如表3[17]所示，管道的建设和运行会影响周围土壤的水热性能，使其发生冻土冻胀现象[18]。为验证本文模型的可靠性，以该地区为例根据现有资料[19],选取冻土模型，尺寸为50 m(长)×10 m(宽)×10 m(高)，冻土层厚度5 m，冻胀区长度10 m。区域管道埋深1.8 m，油压为4 MPa，输油温度随季节变化，管道垂直位移验证如图4(a)所示。通过漠大地区地温监测数据来模拟管道周围土壤温度场变化[20]，地温沿纵深变化验证曲线如图4(b)所示。由图4可以看出，本文管道垂直位移变化与文献[3]中位移变化趋势一致，模拟的土壤温度变化与实测地下土壤温度梯度相似，因此可以验证本文有限元模拟结果的可靠性。

表3 土壤热物理性质[17]

图4 模型验证对比

3 结果与分析

为了获得输油管道在寒季运行对其周围土体的热力影响规律，利用有限元模型模拟含管沟土壤的冻胀，对埋地输油管道进行了热固耦合，分析了管沟参数、土壤温度场多种因素对管道的应力影响。有限元应力云图如图5所示。

图5 有限元应力云图

3.1 温度对管道应力的影响

保持管沟边坡坡度(高∶宽)A为1，沟底加宽裕量K为1 m，根据地温观测数据研究地表温度对管道应力的影响。取地表温度较低的1、2、3、11、12月，分别得到图6所示的管顶和管底沿轴向Von Mises应力随温度变化的曲线。

图6 温度影响下沿轴向Von Mises应力

由图6可知，土体发生冻胀会在管道底部和顶部出现应力集中现象，在管道顶部有3个高风险失效区域，分别处于冻胀区域及非冻胀区与过渡区的交界处，这是因为土壤发生冻胀后产生垂直位移，管土相互作用力会使管道受力变形，管底承受压力，管顶承受拉力。管道顶部最大Von Mises应力位于非冻胀区与过渡区的交界处，随地表温度的降低而增大，即在1月份管道Von Mises应力达到峰值264.09 MPa。管道底部由于土壤的冻胀作用会在冻胀区域和非冻胀区与过渡区的交界处产生3个峰值点，最大Von Mises应力位于冻胀区域中部，随地表温度的降低而增大，即在1月份管道Von Mises应力达到峰值368.98 MPa。

图7(a)中显示了当沟底加宽裕量K=1 m，管沟坡度A为1、1.5和2时，管道顶部与底部在1、2、3、11、12月份中受到的最大Von Mises应力。在管道顶部，当A=2时，管道Von Mises应力受温度影响最大，管道受温度影响变化量为85.38 MPa，当A=1时，管道Von Mises应力受温度影响最小，管道受温度影响变化量为56.84 MPa。在管道底部，当A=1时，管道Von Mises应力受温度影响最大，管道受温度影响变化量为112.17 MPa，当A=2时，管道Von Mises应力受温度影响最小，管道受温度影响变化量为76.52 MPa。

图7 温度影响下最大Von Mises应力

图7(b)中显示了当管沟坡度A=1一定，沟底加宽裕量K为1、1.5、2 m时，管道顶部与底部在1、2、3、11、12月份中受到的最大Von Mises应力。在管道顶部，当K=1 m时，管道Von Mises应力受温度影响最大，管道受温度影响变化量为63.48 MPa，当K=2 m时，管道Von Mises应力受温度影响最小，管道受温度影响变化量为51.06 MPa。在管道底部，当K=1 m时，管道Von Mises应力受温度影响最大，管道受温度影响变化量为73.43 MPa，当K=2 m时，管道Von Mises应力受温度影响最小，管道受温度影响变化量为50.11 MPa。

3.2 管沟坡度对管道应力的影响

在最冷月并保持沟底加宽裕量K=1 m不变的情况下，管沟边坡坡度(高∶宽)A取1、1.5、和2，分别得到了管顶与管底Von Mises应力沿轴向分布的曲线，如图8所示。

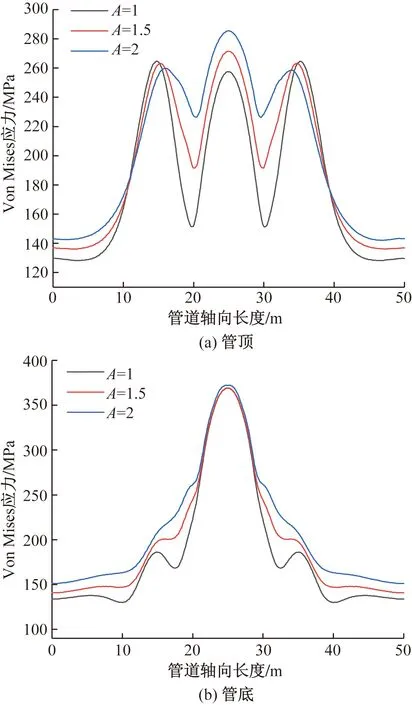
图8 管沟坡度影响下沿轴向Von Mises应力

由图8可知，土体发生冻胀会在管道底部和顶部出现应力集中现象，在管道顶部有3个高风险失效区域，分别处于冻胀区域及非冻胀区与过渡区的交界。在管道底部，由于土体对管道的压力作用，管道在冻胀区域中部出现应力集中现象，形成高风险失效区域。在非冻胀区与过渡区的交界处同样出现应力集中，但随着管沟坡度的增大，应力集中的现象得到了缓解。在沟底加宽裕量一定时，管顶冻胀区域中部最大Von Mises应力随管沟坡度的增大而增大，管沟坡度为2时，最大Von Mises应力为285.46 MPa。管顶非冻胀区与过渡区交界处的最大Von Mises应力随管沟坡度的增大而减小，管沟坡度为1时，最大Von Mises应力为264.09 MPa。管底冻胀区域中部最大Von Mises应力随坡度的增大而增大，管沟坡度为2时最大Von Mises应力为372.07 MPa。当管沟坡度为1时，在非冻胀区与过渡区的交界处出现应力集中现象，此时Von Mises应力为185.99 MPa。

由图9可知，管道底部同一沟底加宽裕量下，管沟坡度为1.5时的最大Von Mises应力相比管沟坡度为1时的最大增量为0.34%，最小增量为0.04%。管沟坡度为2时的最大Von Mises应力相比管沟坡度为1.5时的最大增量为0.79%，最小增量为0.26%。管道顶部同一沟底加宽裕量下，管沟坡度为1.5时的最大Von Mises应力相比管沟坡度为1时的最大增量为6.20%，最小增量为2.81%。管沟坡度为2时的最大Von Mises应力相比管沟坡度为1.5时的最大增量为15.97%，最小增量为8.47%。

图9 管沟坡度影响下最大Von Mises应力

3.3 管沟加宽裕量对管道应力的影响

在最冷月保持管沟坡度比1∶1不变，加宽裕量K取1、1.5、2 m，分别得到了管顶和管底的Von Mises应力沿轴向分布的曲线，如图10所示。

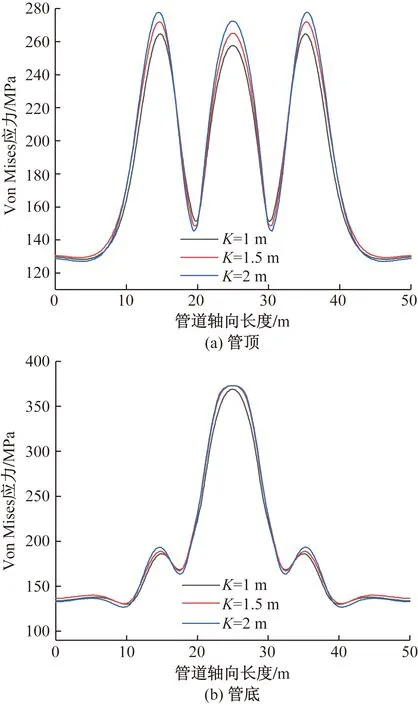
图10 管沟加宽裕量影响下沿轴向Von Mises应力

由图10可知，管顶与管底会因冻胀产生应力集中，分别处于冻胀区域及非冻胀区与过渡区的交界处，最大Von Mises 应力出现在管底冻胀区域中部。当管沟坡度比一定时，最大应力随沟底加宽裕量的增加而增大，冻胀区内管道最大应力为372.8 MPa，位于管底冻胀区中部；非冻胀区与过渡区的交界处也有应力集中出现，最大Von Mises应力为192.4 MPa。管道顶部最大应力为277.7 MPa，位于非冻胀区与过渡区的交界，冻胀区内管道最大应力为272.4 MPa，位于冻胀区域中部。

由图11可知，同一管沟坡度下，管道底部加宽裕量为1.5 m时的最大Von Mises应力相比加宽裕量为1 m时的最大增量为1.15%，最小增量为0.73%。加宽裕量为2 m时的最大Von Mises应力相比加宽裕量为1.5时的最大增量为0.18%，最小增量为0.05%。管道顶部加宽裕量为1.5 m时的最大Von Mises应力相比加宽裕量为1 m时的最大增量为8.72%，最小增量为2.84。加宽裕量为2 m时的最大Von Mises应力相比加宽裕量为1.5 m时的最大增量为5.46%，最小增量为0.94%。

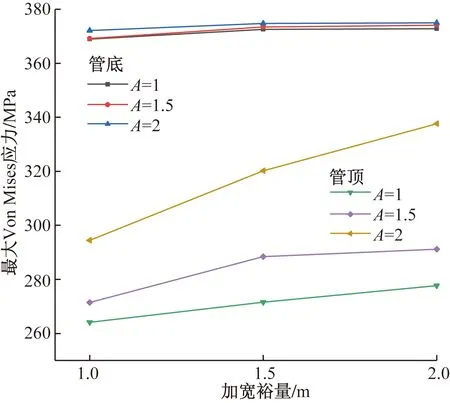
图11 管沟加宽裕量影响下最大Von Mises应力

4 结论

(1)管沟坡度一定时，管道顶部由于冻胀会出现3个峰值，分别位于冻胀区及非冻胀区与过渡区的交界处，且随沟底加宽裕量的增加而增大，最大Von Mises应力出现在非冻胀区与过渡区的交界处。管道底部会出现一个高风险失效区，位于冻胀区域中部，在K=2 m时达到最值。

(2)管沟沟底加宽裕量一定时，管道顶部会因冻胀的发生出现3个峰值，分别位于冻胀区及非冻胀区与过渡区的交界处。在冻胀区域中部，最大Von Mises应力随管沟坡度的增大而增大。在非冻胀区与过渡区的交界处，最大Von Mises应力随管沟坡度的增大而降低。管道底部由于冻胀的发生出现高风险失效区，位于冻胀区域中部，且随沟底加宽裕量的增加而增大。在非冻胀区与过渡区的交界处会出现峰值，但随沟底加宽裕量的增加，应力集中现象会缓解。

(3)管道穿越冻土区时，由于土体在寒季的冻胀现象受地表温度影响较大，管道受土体冻胀的影响在管顶和管顶出现应力集中的现象，分别位于冻胀区域中部及非冻胀区与过渡区的交界处。管道所受应力随地表温度的降低而增大，在最冷月达到最值。当沟底加宽裕量一定时，管沟坡度的增加会增大温度对管道的受力影响。当管沟坡度一定时，沟底加宽裕量的减小会增大温度对含管道的受力影响。