激光武器反无人机集群建模与效能评估

吴 玲,卢俊霖,许俊飞

(海军工程大学兵器工程学院,湖北 武汉 430033)

1 引 言

无人机在近年几次局部战争和冲突中的成功应用,不仅证明了其在军事应用中的广泛前景和巨大优势,也使反制无人机集群技术随之受到各国的高度关注。目前发展出的反制无人机及其集群[1]的主要方法包括电子干扰或压制、激光和微波武器摧毁[2]、火炮或防空导弹摧毁等[3],其中激光武器可以通过对目标施加能量来破坏或摧毁目标,具有速度快、精度高、无弹药量限制、使用成本低等突出优点,被认为是反制无人机系统发展的重要方向。

目前激光武器反制无人机的相关文献主要集中在毁伤效能分析[4-6]、目标跟瞄[7]等问题上,缺乏拦截无人机集群背景下的效能建模和定量评估研究。论文针对无人机集群目标特点,建立集群目标流来袭模型,考虑激光武器对目标的毁伤机理,建立对目标毁伤时间模型,在此基础上建立激光武器拦截无人机集群的排队模型,并在不同态势下评估系统的作战效能和配置需求,可为激光武器作战使用定量研究提供支撑。

2 无人机集群目标流建模

空中集群作战的无人机一般是对海面或地面目标执行侦察探测或察打一体等作战任务。为了建立无人机集群目标流模型,首先应分析集群来袭模式。

根据集群方式、战术特点和任务目标,可将来袭的无人机集群分为集中来袭、连续来袭或随机来袭三种作战模式。集中来袭可表示在短时间内密集到来多架次无人机的情况；连续来袭则可表示多批次、每批多架次无人机按一定时间间隔来袭的情况；随机突击则可表示多架次无人机在空域内游猎侦察等情况。在探测方面,集群无人机目标一般具有“低慢小”目标的特点,早期难以被雷达等探测跟踪传感器所捕获,更多是通过光电跟踪设备发现,由于光电跟踪特点,集群目标往往在发现距离附近以随机数量的目标或目标群形式被发现。因此,可根据上述无人机集群到达的随机性和一定的规律性建立集群目标流模型。

设各批次无人机到达激光武器作用区的时间间隔T为具有独立同分布f(t)的随机变量,分别用以下分布函数来描述在不同来袭模式下无人机集群目标到达的时间间隔。

(1)均匀分布

集中来袭模式下,集群中的无人机目标以较短的时间间隔近似等速率地来袭,设无人机到达防空区的时间间隔服从如下均匀分布:

(1)

其中,a和b分别表示目标到达时间间隔的上下限。

(2)对数正态分布

连续来袭模式下,无人机集群目标可能组织为多批次,每批次按一定时间间隔来袭,此时当每批次无人机起飞时间相同,但飞行时间受导航、控制等多种误差影响时,到达时间间隔则可认为服从对数正态分布:

(2)

其中,μ和σ分别为对数正态分布的期望和均方差。

(3)负指数分布

随机来袭模式即无人机集群中的目标随机到来,此时泊松流可以较好描述目标流的过程特性,即每架无人机到达的时间间隔服从负指数分布:

(3)

其中,λ为单位时间内无人机的到达数量,即到达率,反映出无人机的来袭强度。

上述三种分布可用于描述不同态势下单架或编组无人机的到达间隔,进一步考虑在光电跟踪方式下,单次发现并稳定跟踪目标数量具有一定不确定性,设该数量在[1,N]之间服从均匀分布:

(4)

其中,N为单次发现并可稳定跟踪无人机数量的最大值。

3 激光武器对目标毁伤时间建模

激光武器对目标的毁伤,主要通过发射激光束辐照目标,当辐照能量达到目标毁伤的能量阈值时,目标被毁伤[5]。激光武器毁伤目标的机理较为复杂,不仅在不同的气象条件下有不同的大气传输特性,而且不同的目标材料和激光也存在不同的相互作用,产生不同的响应与毁伤。假定已完成目标毁伤点计算和稳定的跟瞄,在此基础上以所需毁伤时间计算为目的,考虑主要影响因素,建立激光对目标毁伤的评估模型。

假定激光通过辐照毁伤无人机的能量密度阈值为eth,I为高能激光对无人机目标表面的辐照度,tf为激光束持续辐照时间,根据热平衡方程可知,无人机受到有效毁伤应满足以下条件:

I·tf≥eth

(5)

激光武器以激光束照射目标瞄准点,在瞄准点上的激光辐照度分析较为复杂,与激光功率、发射系统中反射镜直径、波长、传输距离、大气传输特性等因素有关。设激光束在瞄准点上形成圆形光斑的面积为S,半径为r,r值不仅与激光传输过程中形成的发散角θ和传输距离L有关,还与激光武器实际射击诸元与理论射击诸元之间的偏差有关,则光斑半径有:

r=θ·L+Δr

(6)

其中,θ为发散角,与激光波长λm成正比,与发射镜直径D成反比,有θ=1.22λm/D；Δr为光斑半径偏差,与真实激光束指向角(由高低角和方位角合成),和理论激光束指向角之间的偏差有关,当指向角偏差为γ时,由于该角度偏差很小,一般可认为垂直入射条件下辐照距离L处目标的光斑半径误差为L·γ。

因此光斑面积为:

(7)

当激光能量分布近似为高斯分布时,垂直入射条件下激光瞄准点对应光斑的辐照度可表示为:

(8)

其中,P0为发射激光束功率；η1为发散系数,取值由84 %到98 %变化,具体数值视光束特性和激光器的光学系统而定；η2为激光在大气传输距离为L时受到如大气折射和吸收等因素导致的能量衰减率,可记为:

η2=(1-α)L

(9)

其中,α为激光束的大气衰减系数,其取值范围受地区和气候影响。

由式(5)～式(9)可知,激光武器毁伤无人机目标所需持续辐照时间tf可通过下式求解得到:

(10)

其中,L(t)为持续照射目标过程中t时刻目标的距离。

4 激光武器拦截无人机集群排队模型与仿真

4.1 系统排队模型

将来袭无人机集群视为顾客流,将激光武器视为服务台,建立排队模型,分析不同情况下激光武器拦截无人机集群的效能及兵力需求。

首先作如下假设:①防空系统由m部激光武器组成,每部激光武器对无人机的拦截区远近界相同,且均在工作时长T0后需准备T1时长以继续投入作战；②单部激光武器在同一时刻仅拦截一架无人机,拦截所需时间根据激光武器性能和目标距离由式(10)给出；③进入防区的无人机一经发现即可完成稳定的跟踪瞄准,每架无人机仅由一部激光武器实施拦截；④无人机进入防区后,若有激光武器处于可用时间(空闲且处于可工作时间),且满足武器拦截时间要求,则实施拦截；若无可用激光武器,则继续飞行,直至有可用武器实施拦截,或飞出拦截近界实现突防。

因此为该问题建立如下排队模型:

1) 输入过程:顾客数有限,每次发现目标的时间间隔按照不同模式分别服从式(1)～(3)所描述的某种分布,每次发现的目标数服从式(4)分布；

2) 排队规则为先到先服务,且逗留时间有限的混合制排队规则；

3) 服务机制为单队列多服务台并联方式,单服务台每次仅为单个顾客提供服务,服务时间服从相互独立的随机分布,由公式(10)给出。

为评估激光武器反制无人机集群目标流的效能,采用目标突防概率和武器服务强度作为排队系统效率的评价指标,其中服务强度为单个激光武器用于拦截目标的时间和准备时间之和占总时间的比值。

4.2 仿真计算与结果分析

4.2.1 激光武器对目标毁伤时间仿真

首先结合式(10),对激光武器毁伤目标时间随目标距离和激光功率变化的情况进行仿真。假定发射激光波长为1.06 μm,发散系数为0.84,大气衰减系数为0.35,激光通过辐照毁伤无人机的能量密度阈值为0.4×10-6J/m2,发散镜直径为0.3 m,光斑半径偏差为0.3 m。激光束功率从0.2～1 MW变化,目标距离从1～6 km变化时,激光武器毁伤目标所需辐照时间如图1所示。

图1 毁伤目标时间随目标距离和激光束功率变化关系

图1仿真结果表明了激光武器毁伤目标时间随发现目标距离和武器功率之间的一般关系,即距离越近、功率越大,毁伤时间越短,利用这一模型模拟武器毁伤目标时间是合理有效的。式(10)给出的毁伤时间模型是在一定简化条件下仅考虑主要影响因素所得到的模型,实际问题中可跟据武器、目标、环境对模型参数进行修正。

4.2.2 目标突防概率与武器数量关系仿真

考虑无人机集群目标以不同模式和不同强度来袭时,无人机突防概率与激光武器数量之间的关系。假定集群分别采用集中突击、连续突击或随机突击模式来袭,集群中无人机目标的来袭时间间隔分别服从均匀分布、对数正态分布和负指数分布,每次发现(到达)的无人机目标数量在1至3架间服从均匀分布；发现目标的初始距离服从均值为2000 m,均方差为500 m的正态分布,无人机为速度20 m/s；假定一经发现目标即能保持对目标的稳定跟踪,且一发现目标时若有武器空闲,且无人机临空时间满足武器一次毁伤时间要求即实施对目标的拦截,激光武器一次拦截对无人机的毁伤概率为0.7；一次拦截后若未成功则空闲武器在满足拦截时间要求的条件下可继续对目标实施拦截；假定激光武器功率为0.2 MW,每拦截目标50 s后,需间隔100 s时间以完成武器准备工作。

分别在较高来袭强度、中等来袭强度、低来袭强度下进行了仿真,其中较高强度的集中来袭模式下相邻无人机到达时间间隔服从(5,15) s内的均匀分布,连续来袭模式下时间间隔服从期望值为10、均方差为10的对数正态分布,随机突击模式下时间间隔服从参数为1/10的负指数分布；中等强度则上述参数分别设均匀分布为(15,25),对数正态分布为(20,10),负指数分布参数为1/20；低强度相应参数则设均匀分布为(25,35),对数正态分布为(30,10),负指数分布为1/30。对稳态情况下目标突防概率的仿真结果如图2和表1所示。

由图2和表1仿真结果可得如下结论:

1)在相同来袭强度下,不同来袭模式对无人机目标最终突防概率差异不显著,但采用随机来袭模式的无人机集群在几乎各个来袭强度下都获得了最高的突防概率,可见随机来袭模式的无人机集群在防空作战中较难应对；后续仿真中均针对随机来袭模式开展仿真分析。

2)随着激光武器数量增加,无人机突防概率逐渐下降,但继续增加武器数量所获得拦截效能提升程度明显降低,如图2(a)中激光武器数量从4座增加到6座,突防概率最高仅下降了0.03；图2(b)和(c)中,武器数量从3提升到6,突防概率最高下降不足0.003。可见,应根据可能面临的无人机集群目标强度,结合激光武器性能和期望的拦截效能,合理确定配置的武器数量。例如在仿真给定的激光武器性能条件下,对到达时间间隔服从参数为λ=0.1的负指数分布的较高强度来袭的无人机集群目标,要达到90 %以上的拦截概率,由表1可知需配置2座激光武器。

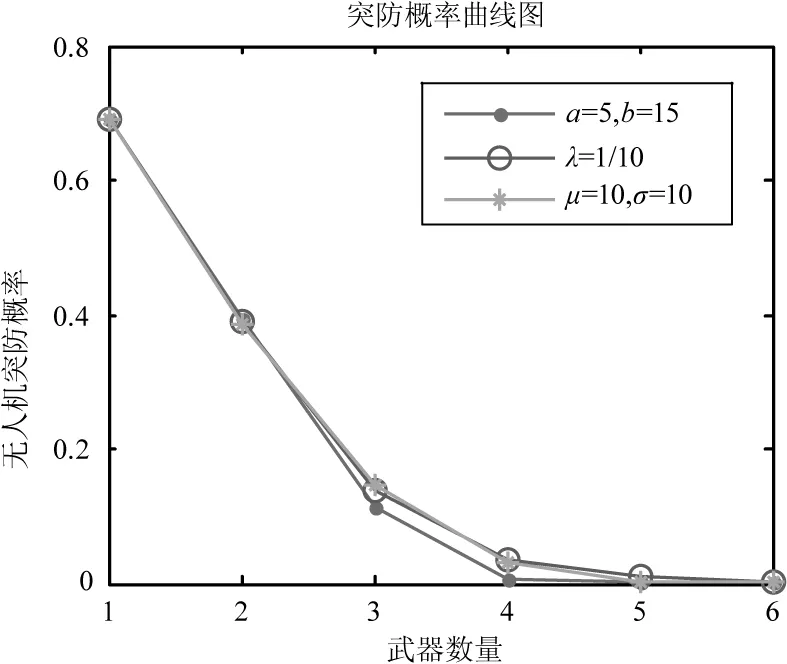
(a) 较高来袭强度

(b) 中等来袭强度

(c) 较低来袭强度

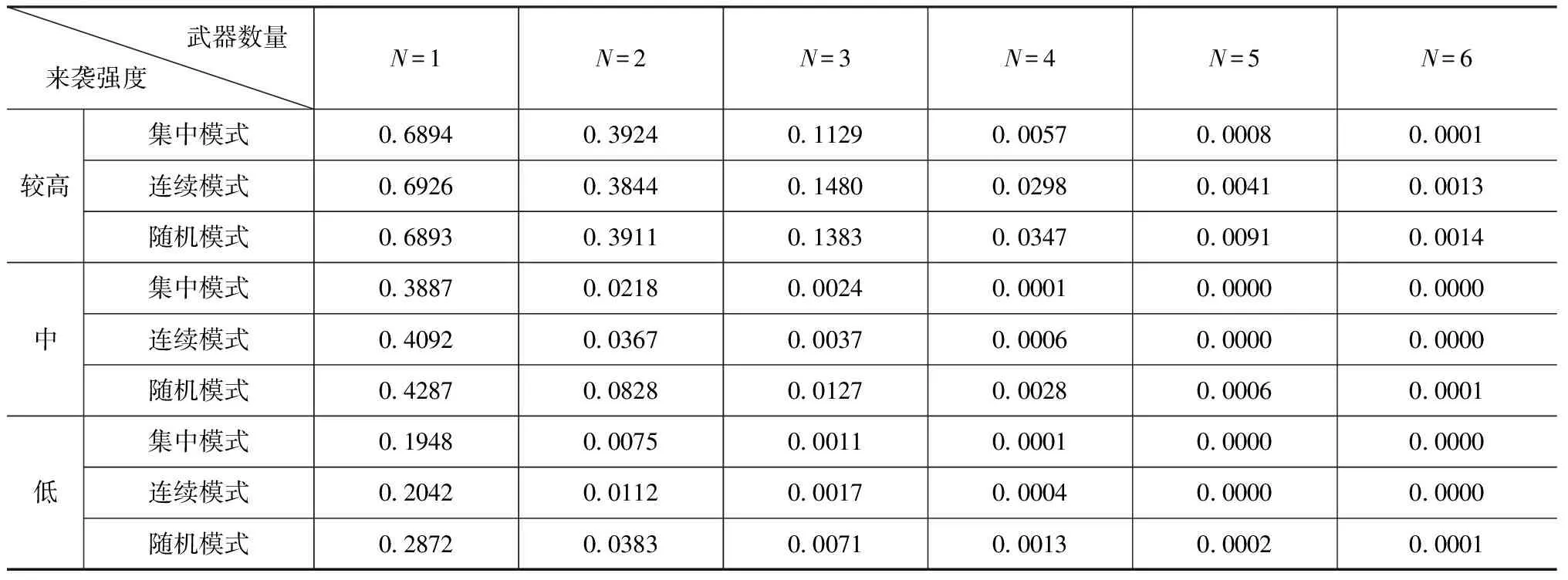
表1 不同武器数量和来袭强度下的无人机集群目标突防概率

4.2.3 激光武器性能对无人机集群突防概率影响仿真

其他条件如3.2.2节仿真,进一步仿真分析在2座激光武器、不同来袭目标强度下,无人机突防概率随激光武器功率变化情况,结果如图3(a)所示；假定武器每连续工作50 s后,需间隔一段时间完成武器准备工作,在2座激光武器、不同来袭强度下,武器准备时间从50 s到500 s条件下突防概率的变化关系如图3(b)所示；无人机来袭间隔服从λ=0.2的负指数分布,即高强度来袭条件下,武器对目标毁伤概率从0.1～0.9变化条件下,目标突防概率情况如图3(c)所示。

由图3可知,激光武器功率对拦截效果影响较大,在仿真假设条件下要对较高强度来袭的无人机集群达到90 %拦截概率,则激光武器功率至少应达到0.4 MW；武器有效投入使用的时间同样影响拦截效果,可持续使用时间越长、间断准备时间越短,对目标拦截效果越好；单次射击条件下武器对目标毁伤概率越高,拦截效果越好。在模型中考虑激光武器性能中的上述不同因素,有效反应了对无人机集群拦截的综合效果。

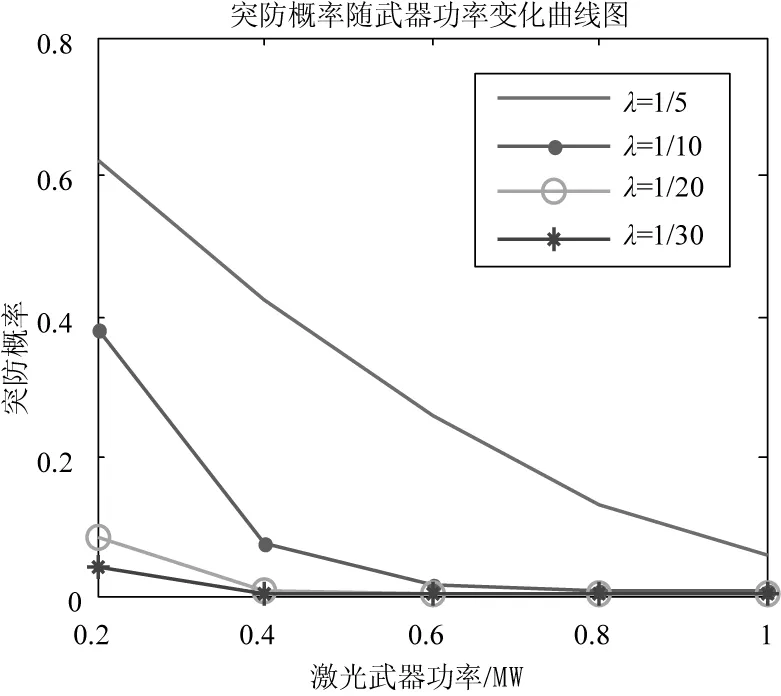
(a)

(b)

(c)

通过以上仿真可知:

1)可以利用三种分布描述不同集群模式下无人机目标流,其中随机来袭模式的无人机集群相对较难防御；

2)建立排队论模型来评估激光武器对无人机集群的拦截效果是有效的,在模型中可以综合考虑无人机集群目标来袭特点和强度、激光武器的性能和数量,武器作战运用方式等因素,从而较为全面和合理地评估激光武器反无人机集群的作战效能；

3)利用所建立的排队论模型,可以进一步获得在给定的来袭目标特点和要达到的作战效能指标条件下的武器数量、性能等配置方案,为实际作战运用提供支撑。

5 结 论

激光武器被认为是反无人机集群作战的有效手段。建立了不同来袭模式下的无人机集群目标流模型,和激光武器对无人机目标的毁伤时间模型,在此基础上建立激光武器反无人机集群的排队模型,仿真分析了防空效能的主要影响因素。结果表明,利用本文提出的方法可在给定条件下计算得到反无人机集群的效能指标,也可利用该方法获得给定作战效能指标下的合理的武器配置方案。