外压圆筒小加强圈设计的改进方法
2022-07-10陈冰冰徐佳伟张艺奇高增梁
陈冰冰,徐佳伟,徐 伦,张艺奇,高增梁
(1.浙江工业大学 化工机械设计研究所,杭州 310023;2.浙江工业大学 机械工程学院,杭州 310023;3.过程装备及其再制造教育部工程研究中心(浙江工业大学),杭州 310023)
符号说明:
As——小加强圈横截面积,mm2;
Do——筒体外直径,mm;
e——圆筒最大初始缺陷幅值(绝对值为最大值),mm;
Ey——筒体材料杨氏弹性模量,GPa;
Ers——加强圈材料杨氏弹性模量,GPa;
Et——切线模量,GPa;
Fha——周向压缩薄膜应力,MPa;
Fhe——小加强圈间筒体的预期弹性屈曲应力,MPa;
Fhef——大加强圈间筒体的预期弹性屈曲应力,MPa;
Fic——预期屈曲应力,MPa;
FS——设计系数;
hw——加强圈截面高度,mm;
Is——小加强圈实际截面惯性矩,mm4;
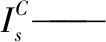

L——外压筒体计算长度,mm;
LB——大加强圈与相邻两侧加强圈间距之和的一半,mm;
Le——筒体有效长度,mm;
Ls——小加强圈与相邻两侧加强圈间距之和的一半,mm;
n——筒体预期屈曲波数;
Ns——小加强圈个数;
Pa——按ASME BPVC.Ⅷ.2计算的加强圈间筒体许用外压,MPa;
Pal——按ASME BPVC.Ⅷ.2计算的大加强圈间筒体许用外压,MPa;
Pas——按ASME BPVC.Ⅷ.2计算的小加强圈间筒体许用外压,MPa;
Pc——设计外压,MPa;
Pf——模拟得到的屈曲外压,MPa;
Pt——试验得到的屈曲外压,MPa;
Py——圆筒屈服压力,MPa;
Rc——加强圈组合截面形心至圆柱壳轴线的半径,mm;
Sy——筒体材料屈服强度,MPa;
Srsy——加强圈材料屈服强度,MPa;
tw——加强圈截面厚度,mm;
Zs——壳体中径至小加强圈形心的径向距离,mm;
β——与ASME BPVC.Ⅷ.2的设计裕度的对比因子;
δ——圆筒厚度,mm;
η——设计因子;
υ——泊松比;
ξ——屈曲临界压力与屈服压力比。
0 引言
压力容器设计标准中的小加强圈设计方法,是基于理想几何形状情况下的理论公式,并考虑一定安全系数得出的。1953年,KENDRICK[1]提出了理想几何形状情况下带加强圈圆筒临界失稳压力的计算方法。基于“Kendrick理论”推导的、计算带加强圈圆筒整体屈曲压力的Bryant公式[2],为ASME Boiler & Pressure Vessel Code Section Ⅷ,Division 2(以下简称ASME BPVC.Ⅷ.2)、API 2U以及EN 13445 Unfired Pressure Vessels (以下简称EN 13445-3)等标准规范中小加强圈的设计提供了理论依据。
围绕带加强圈外压圆筒的稳定性问题,研究人员进行了大量试验与模拟研究[3-11]。MILLER等[3]指出,带加强圈圆筒的初始几何缺陷会对整体屈曲压力产生一定的影响,而理论公式法对初始几何缺陷的探讨具有局限性。1985年,TSANG等[4]对比了外压作用下,带小加强圈圆筒失稳压力的试验值和数值模拟结果,提出GMNIA(考虑初始几何缺陷的几何材料双非线性分析)数值模拟方法得到的失稳压力值与试验值吻合度较好,可用于含初始几何缺陷的、带加强圈外压圆筒稳定性问题的数值模拟研究。
目前,我国现行的压力容器设计标准GB/T 150.1~150.4—2011《压力容器》、JB 4732—1995(R2005)《钢制压力容器——分析设计标准》和ASME Boiler & Pressure Vessel Code Section Ⅷ,Division 1(以下简称ASME BPVC.Ⅷ.1)中,采用的是单一规格加强圈的设计方法。而如ASME BPVC.Ⅷ.2和EN 13445-3均已引入了大、小加强圈的设计方法。从我国目前正在修订的压力容器分析设计标准的征求意见稿来看,引入与ASME BPVC.Ⅷ.2中相一致的大、小加强圈的设计方法将成为趋势。
带加强圈外压圆筒的可能屈曲形式分为几种情况:局部壳体屈曲、加强圈局部屈曲和整体屈曲等(如图1[12]所示)。局部壳体屈曲是指屈曲发生在两加强圈之间的壳体上;加强圈局部屈曲是指加强圈元件上发生屈曲;整体屈曲是考虑圆筒与加强圈一起发生屈曲的情况。
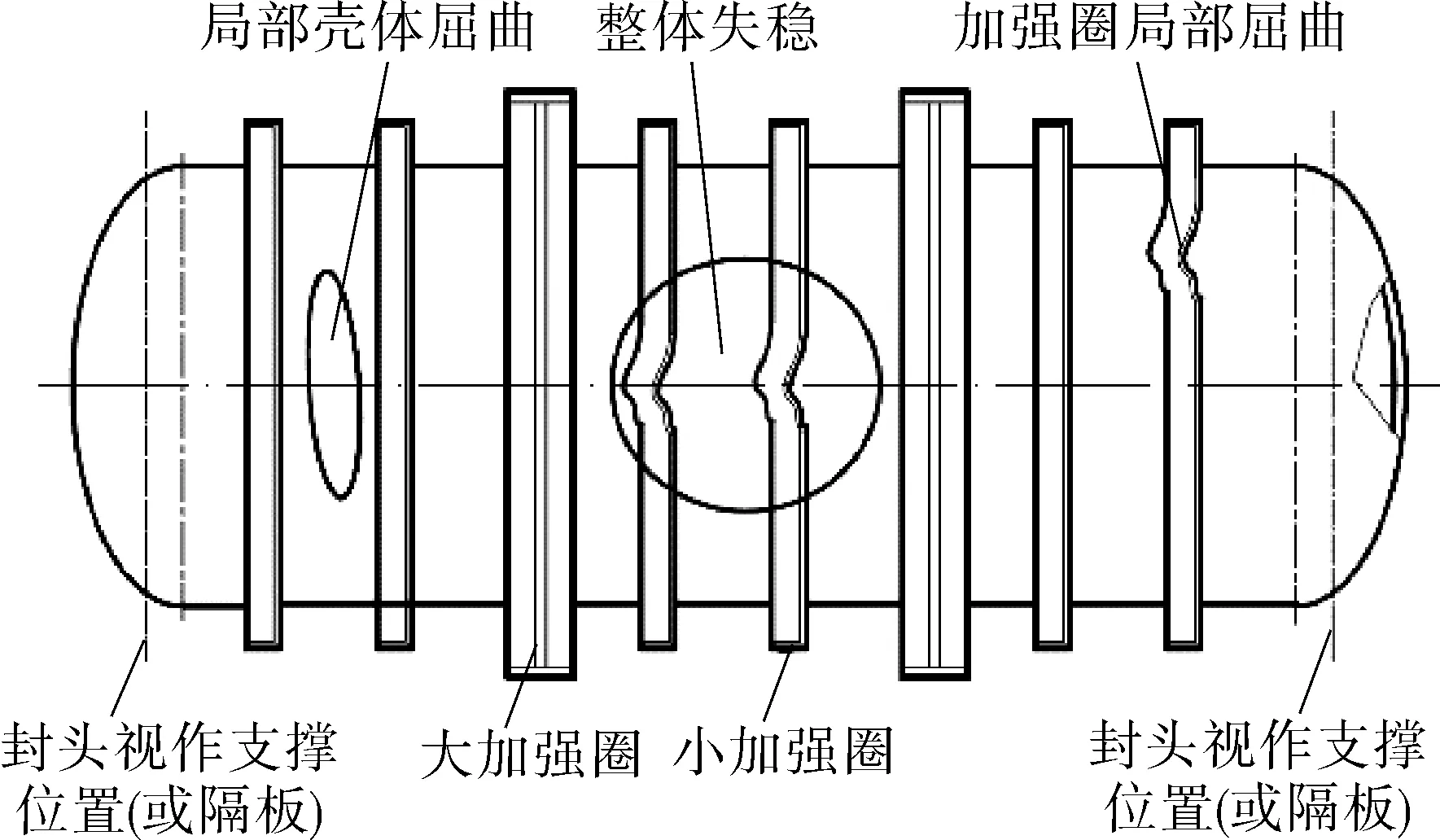
图1 带加强圈外压圆筒屈曲形式示意Fig.1 Schematic diagram of buckling form of cylinder with stiffening ring

(1)
(2)
带小加强圈的外压圆筒屈曲模态按两大加强圈或支撑线之间的筒体(长度为LB)整体屈曲的模态考虑。
ASME BPVC.Ⅷ.2与GB/T 150.3,ASME BPVC.Ⅷ.1中的加强圈设计思路是不同的,采用单一规格加强圈按ASME BPVC.Ⅷ.2计算得到的所需惯性矩与GB/T 150.3的计算结果可能会相差很大。在ASME BPVC.Ⅷ.2中,设计要求加强圈能保证筒体在计算长度Ls上承受预期弹性屈曲应力Fhe作用而不发生屈曲。因此,由预期弹性屈曲应力Fhe(Fhe由筒体结构尺寸决定,与设计外压无关)计算得到许用外压Pa,若设计外压Pc小于许用外压Pa则表明合格。而在ASME BPVC.Ⅷ.1和GB/T 150.3中,加强圈的设计是直接基于设计外压Pc的。对于工程上存在内压和外压多种工况的压力容器设计,容器壁厚δ可能由较危险的内压工况确定,此时的壁厚δ对外压工况而言存在余量。按较厚圆筒计算的预期弹性屈曲应力Fhe会较大,导致得到的小加强圈尺寸也会偏大。
例如,某在役800万吨/年常减压装置中的减压塔,由4段各带单一规格加强圈的圆筒组成。4段带加强圈圆筒结构参数见表1,圆筒和加强圈材料为Q345R,设计外压Pc=0.1 MPa,设计温度410 ℃,材料性能参数见表2。

表1 4段带加强圈圆筒结构参数Tab.1 Structural parameters of cylinder with 4 sections of stiffening ring

表2 设计温度下Q345R材料性能参数Tab.2 Material parameters at design temperature of Q345R

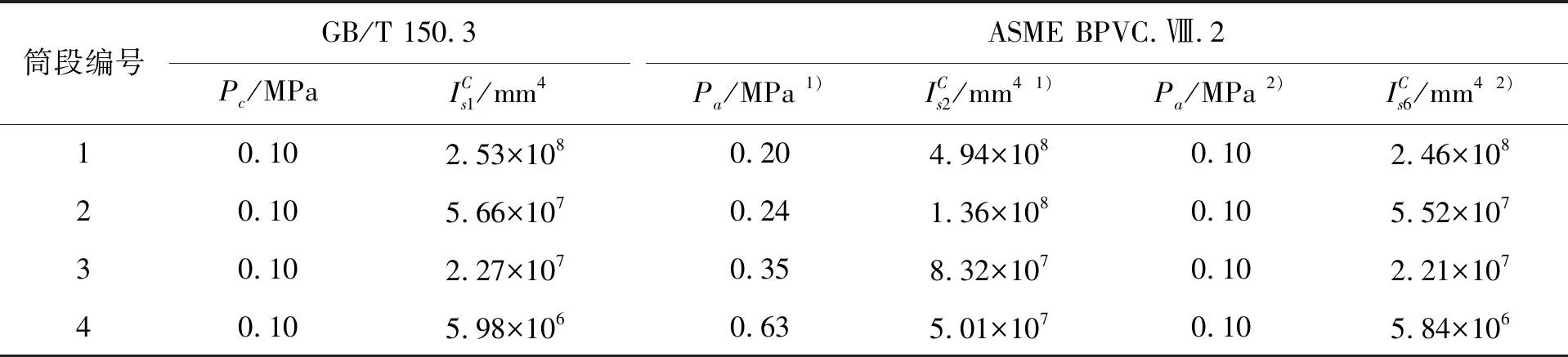
表3 两种标准计算结果Tab.3 The calculation results of the two standards
1 改进设计方法的构想
1.1 加强圈数量间距选择
根据设计外压Pc和圆筒长度LB,按ASME BPVC.Ⅷ.2中许用外压的计算公式,先计算大加强圈间圆筒许用外压Pal。若Pc
1.2 小加强圈间筒体预期弹性屈曲应力的计算
求设计外压下的周向压缩薄膜应力Fha:
Fha=PcDo/2δ
(3)
考虑到Fha中隐含有设计系数[13],满足设计外压所对应的预期屈曲应力Fic为:
(4)
查材料的应力-应变曲线本构模型,可得切线模量Et,由下式算得弹性屈曲周向应力Fhe:
(5)
小加强圈与筒体有效长度组成的复合截面惯性矩需满足公式(2)。n为采用公式(6)计算并取整数,当n小于2时取2,n大于10时取10。
(6)
由公式(7)计算调整结构尺寸,使得小加强圈组合截面惯性矩大于所需惯性矩的要求。
(7)
本改进方法的核心思想是基于设计外压进行小加强圈设计,避免采用基于与结构相关的预期弹性屈曲应力Fhe,该方法在文中简称为“改进方法”。
2 数值模拟方法的确定
带加强圈外压圆筒存在不同屈曲形式,加厚圆筒厚度可能使原来局部壳体屈曲转变为整体屈曲,情况复杂。影响屈曲临界压力的因素也有很多,如初始几何形貌缺损、材料的非线性、加强圈自身的刚度等。带加强圈外压圆筒的屈曲临界压力很难通过理论方法进行准确预测。近年来,随着模拟计算技术的快速发展,研究出采用计及带初始几何缺损不完美结构形状的几何与材料双非线性分析的数值模拟方法(GMNIA),将初始几何缺损、材料的非线性、加强圈自身的刚度等影响因素纳入到模拟计算中,可以预测外压圆筒临界压力。常见的屈曲GMNIA数值模拟方法有一致模态法,它是按结构特征模态施加几何形貌缺损,不能完全反映实际的几何形貌缺损特征,该方法的准确度不高。文献[14]给出了一个具有一定的普适性、基于傅里叶级数法GMNIA模拟方法,能比较准确地预测外压圆筒临界压力。该方法采用“简化傅里叶级数法”来描述筒体的初始几何形貌缺损特征[14],其公式如下:
(8)
式中,Fl,Ekl,φkl的数据详见文献[14];k为轴向半波数;l为周向全波数;z为圆筒轴向距离。
文献[14]的方法是针对不带加强圈外压圆筒。对于带加强圈外压圆筒,若忽略加强圈几何形貌缺损的影响,即可采用文献[14]中“简化傅里叶级数法”模型描述带几何形貌缺损的圆筒,此时加强圈则按理想的几何形貌考虑,然后采用几何与材料双非线性数值模拟方法进行模拟计算,该方法简称为IM-F-GMNIA法。下面的模拟分析验证结果表明,IM-F-GMNIA法是切实可行的,能较好预见带加强圈圆筒的临界屈曲压力。
MILLER等[3]提供了19组带加强圈卷焊圆筒的数据和试验结果;CHO等[5]提供了9组环焊加工的带加强圈卷焊圆筒数据和屈曲试验详细结果,其主要数据见表4。

表4 文献[3,5]中的试样数据和试验值Tab.4 Sample data and experimental values in literature[3,5]
按IM-F-GMNIA法思路,建立带初始几何缺损有限元计算模型。采用双线性材料模型(材料第1段弹性模量为杨氏弹性模量Ey,屈服点之后的第2段弹性模量为Ey/100),泊松比取0.3。采用Abaqus有限元分析软件进行计算,单元为S4壳单元,圆筒两端的边界条件设为简支边界条件,计算时考虑几何大变形行为,采用Static Riks分析方法(弧长法)。IM-F-GMNIA法的计算模型最终模拟得到的临界屈曲模态与文献[3,5]实物试验结果的对比如图2所示。图2右边为试样SR-4,SR-9,SR-Ⅱ模拟计算所得的临界屈曲模态,与文献[5]中试验现象(见图2左边)吻合良好(注:发生的周向位置无法预测)。

(a)SR-4
图3将IM-F-GMNIA法和“一致模态法”的模拟结果与文献试验值对比,其中“一致模态法”的结果较实验值整体偏小,不如IM-F-GMNIA 法准确,故本文后续的数值模拟选择采用IM-F-GMNIA法。

图3 临界屈曲压力数值模拟值与实物试验结果的对比Fig.3 Comparison between numerical simulation and experimental results of critical buckling pressure
3 数值模拟试验
为验证所提出改进方法的可行性,将采用IM-F-GMNIA法进行数值模拟试验。引入因子η表示设计外压的变化,η定义式如下:
(9)
当η=0,Pc=Pal,设计外压等于不带加强圈时圆筒的许用外压,表示该设计外压下可不设置加强圈;当η=1,Pc=Pas,设计外压等于加强圈间圆筒的许用外压,继续增加加强圈惯性矩已不起作用。对于给出的加强圈数量,η从0~1之间变化,将有一个对应的加强圈惯性矩。进一步分析可知,文中给出的小加强圈改进方法,在η=1时与ASME BPVC.Ⅷ.2相同,所以这种情况也代表ASME BPVC.Ⅷ.2情况,模拟计算的临界压力也相同,均为PfASME。
为不失一般性,数值模拟试验选择了两种类型的圆筒试样,使去除加强圈后的圆筒的屈曲波数n分别为2和5,以代表长圆筒和短圆筒。材料的杨氏弹性模量Ey取200 GPa,泊松比取0.3,屈服强度(按压力容器常用材料Q345R的屈服强度345 MPa取值)与杨氏弹性模量之比(Sy/Ey)为1.725×10-3。
3.1 长圆筒类型(n=2)的模拟计算试样的安排
长圆筒类型的模拟试验安排见表5,考察因子η从0~1的变化。S系列主要考察加强圈数量不变而圆筒长度和直径发生变化的情况;J系列为圆筒长度和直径不变而加强圈数量发生改变的情况。其中,S9-X试样的建模尺寸为J5-X的2倍,用于考察L/Do,Do/δ,e/δ都不变时,实际建模尺寸的缩放对模拟结果是否存在影响;S10-X筒体总长为S8-X的2倍,用于考察长圆筒类型中加强圈间距不变时,总长度的增加对模拟结果是否存在影响。

表5 模拟计算试样尺寸(n=2)Tab.5 Size of simulated sample (n=2)

表6 试样的加强圈尺寸(n=2)Tab.6 Size of stiffening ring (n=2)
3.2 短圆筒类型(n=5)的模拟计算试样的安排
短圆筒类型(n=5)的模拟试验安排见表7,考察因子η从0~1的变化。H系列为圆筒长度和直径不变而加强圈数量发生改变情况,其中,H7-X试样的建模尺寸为H3-X试样的1/2,用于考察L/Do,Do/δ,e/δ都不变时,实际建模尺寸的缩放对模拟试验结果是否存在影响。

表7 模拟计算试样尺寸(n=5)Tab.7 Size of simulated sample (n=5)
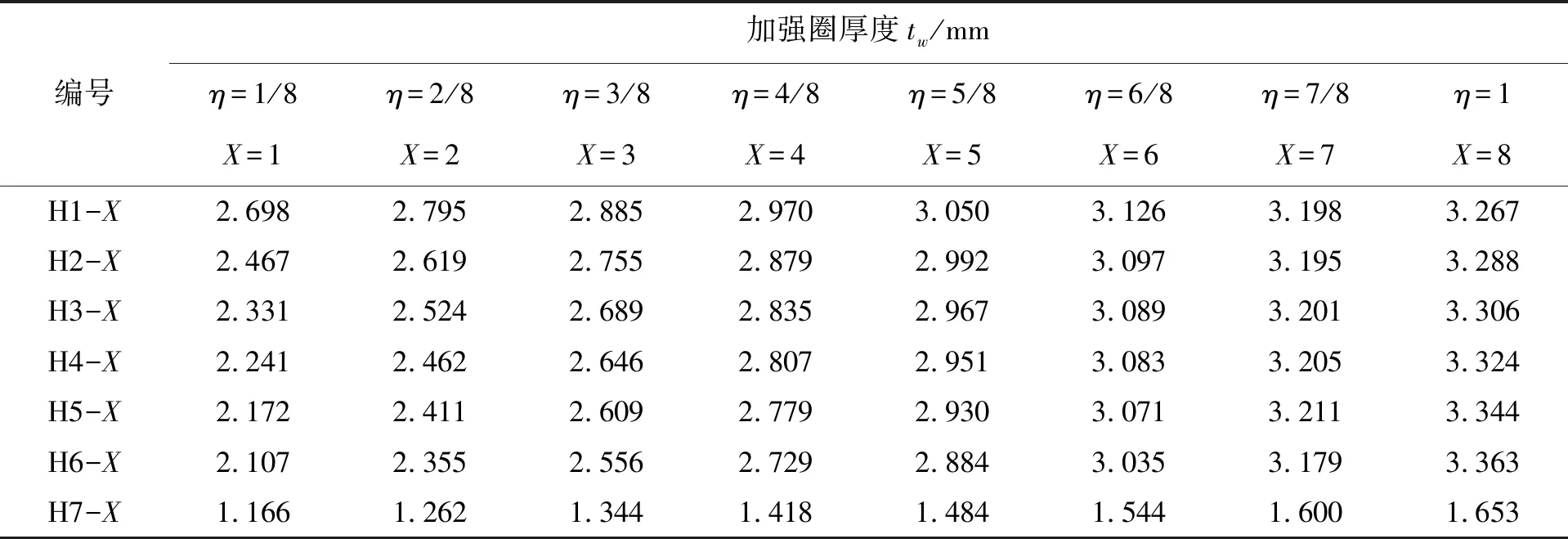
表8 试样的加强圈尺寸(n=5)Tab.8 Size of stiffening ring (n=5)
4 结果与讨论
采用IM-F-GMNIA法对第3节安排的小加强圈外压圆筒模型进行数值模拟试验,得到临界屈曲模态和临界屈曲压力Pf。将模拟结果在径向位移最大点处作横截面,呈现出后屈曲模态的该横截面上的变形图。

(a)η=1时加强圈数量变化
先以J系列6组圆筒为例,分析去除加强圈后圆筒为长圆筒(n=2)时临界屈曲模态情况。当η=1时,加强圈数量从1个增加至6个时,明显可见屈曲发生在加强圈的筒节之间,如图4(a)所示。加强圈的筒节长时,为2波屈曲;加强圈的筒节较短时,加强圈的筒节间出现多波屈曲。当η从0~1变化时,屈曲模态变化如图4(b)所示,随着η增大,试样的加强圈结构所需的尺寸也增大,屈曲模态也发生改变。可以看出,试样J5-1~J5-3屈曲模态为整体屈曲,屈曲波数与长圆筒一致,均为2;试样J5-4既有筒间局部屈曲,也有整体屈曲;随着加强圈的增大,试样J5-5~J5-8加强圈间筒体的局部屈曲现象越发明显,此时加强圈起到支撑线作用。
去除加强圈后圆筒为短圆筒(n=5)时临界屈曲模态如图5所示。当η=1时,加强圈数量从1个增加至6个时,明显可见屈曲发生在加强圈的筒节之间,大加强圈间筒体的失稳波数随加强圈数量的增加而增加。当η从0~1变化时,随着η增大,试样的加强圈结构所需的尺寸也增大,屈曲模态局部呈现复杂变化,断面在临界状态下的最大径向位移变化不明显。

图5 屈曲模态断面变形图(n=5)Fig.5 Deformation of the buckling mode section (n=5)
由外压圆筒的屈曲理论可知,临界压力的大小仅与L/Do,Do/δ,e/δ直接相关。为此专门安排了对比试样,S9-X试样的建模尺寸为J5-X的2倍,H7-X试样的建模尺寸为H3-X的1/2,用于考察L/Do,Do/δ,e/δ不变,实际建模尺寸的缩放对模拟结果是否存在影响。另外,为考察去除加强圈后的长圆筒(n=2)总长增加时,是否会对临界压力产生影响,对S8-X和S10-X作对比,S10-X筒体总长较S8-X增加了1倍,保持加强圈间距不变。对比试样的模拟结果如表9所示。结果表明,临界压力相差很小,进一步说明临界压力只与L/Do,Do/δ,e/δ直接相关。增加去除加强圈长圆筒的总长对临界压力的影响也很小。
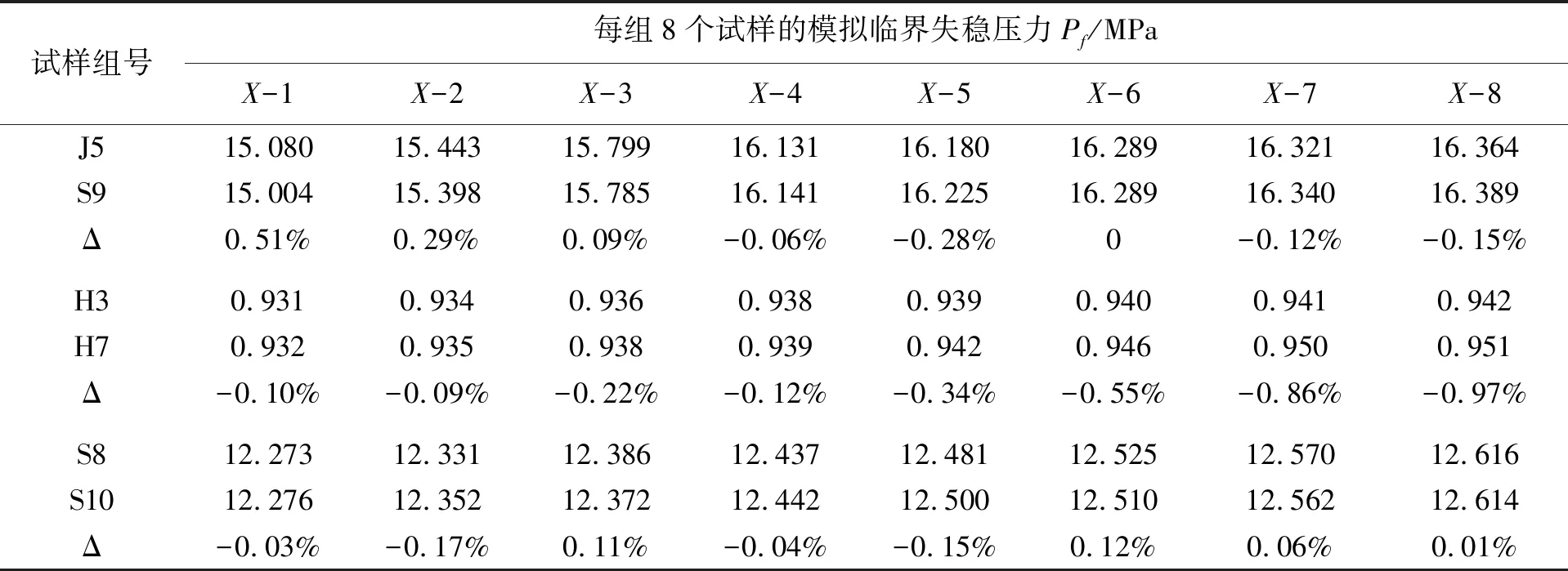
表9 对比试样模拟结果Tab.9 Comparison of sample simulation results
由外压圆筒的屈曲理论可知,材料弹塑性会对临界屈曲压力产生影响,引入参数ξ来表示圆筒屈曲临界压力与屈服压力关系,定义式如下:
ξ=Pf/Py
(10)
同时,引入对比因子β,表示本改进方法的设计裕度与ASME BPVC.Ⅷ.2的设计裕度之间的关系。β定义式如下:
(11)

(a)S系列
(a)S系列
Pc为设计外压,在Pal~Pas之间,对于给定的圆筒结构和小加强圈数量,按本改进方法,得到小加强圈的惯性矩,给出小加强圈尺寸,进一步模拟计算算得到Pf。同样,按ASME BPVC.Ⅷ.2可得许用外压为Pas,同时得到小加强圈的惯性矩,给出小加强圈尺寸,进一步模拟计算得到PfASME。式(11)中分子表示本改进方法的设计裕度,分母表示ASME BPVC.Ⅷ.2的设计裕度。若对比因子β大于1,则表明改进方法的设计裕度比ASME BPVC.Ⅷ.2标准的可接受设计裕度会更大。
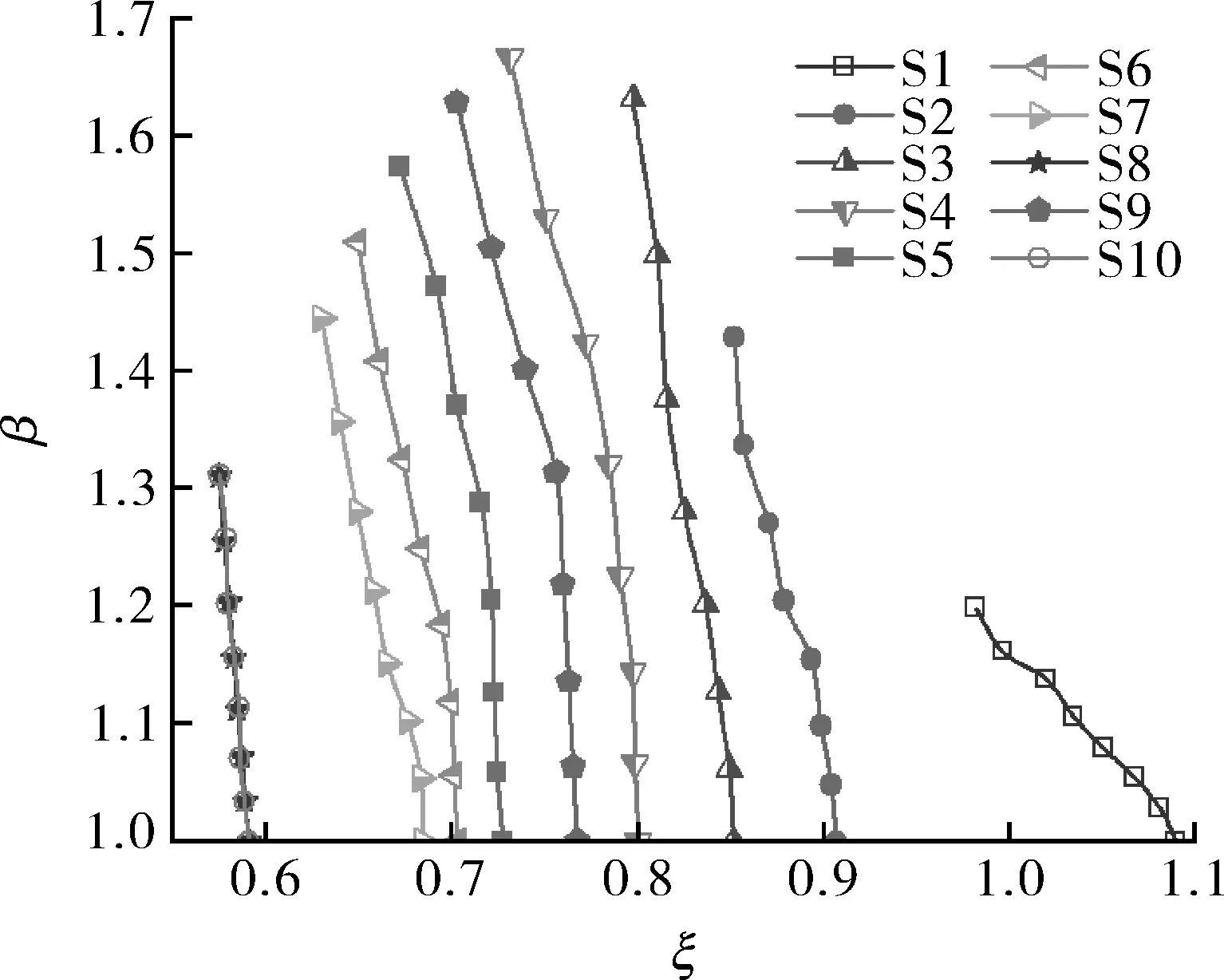
模拟计算结果表明,对比因子β随因子η和ξ的关系如图6所示,且所有对比因子β都大于1,这表明本改进方法的设计裕度不低于按ASME BPVC.Ⅷ.2标准的可接受设计裕度。
图6中,因子η减少时,对比因子β增大。这表明,若因子η减少(设计外压的减小),按本改进方法,加强圈所需的惯性也将减少,但相对于AMSE BPVC.Ⅷ.2可接受的设计裕度,本改进方法可接受的设计裕度将会升高。
图7更清楚地反映出对比因子β随因子ξ的变化关系(ξ可表征带小加强圈筒体结构的弹塑性程度)。所有β-ξ曲线在ξ方向均呈显著下降的趋势,对相同规格、相同小加强圈布局的圆筒,当加强圈规格增大,ξ值增加,对比因子β将沿曲线快速减小至最低值1.0。对相同径厚比Do/δ的圆筒,小加强圈数量越多、加强圈间距越小,则结构整体的塑性就越大,β-ξ曲线整体将越偏右。比较两种径厚比Do/δ的圆筒S,J系列与H系列,D/t大的H系列圆筒在设置加强圈后,因结构更偏向弹性阶段,导致ξ值普遍更小,且对比因子β普遍更高,说明其相对于AMSE BPVC.Ⅷ.2可接受的设计裕度要更大。

表10 改进方法与各标准计算结果比较Tab.10 Comparison of calculation results by the improved method and the standard method
5 结论
(1)在ASME BPVC.Ⅷ.2方法的基础上,文中提出一种基于设计外压的小加强圈设计改进方法,使小加强圈惯性矩与设计外压直接关联,该方法较ASME BPVC.Ⅷ.2中的设计方法更为合理。
(2)基于文献[14]中的“简化傅里叶级数法”模型,给出了一种优于“一致模态法”且能较好预测带加强圈圆筒临界屈曲压力的数值模拟方法(IM-F-GMNIA法),该模拟方法的计算结果与实物试验结果吻合良好。
(3)采用IM-F-GMNIA法进行了数值模拟试验,较系统地考察了去除加强圈后圆筒的屈曲波数n为2或5、屈曲临界压力与屈服压力比ξ的范围为0.22~1.09情况下,设计裕度对比因子β与加强圈圆筒参数η,ξ的关系。结果表明,所提出的外压圆筒小加强圈设计改进方法的设计裕度将不低于ASME BPVC.Ⅷ.2方法可接受的设计裕度。
