基于信号分解和切比雪夫多项式的多体系统区间不确定性分析方法1)

蒋 鑫 白争锋,†,2) 宁志远 王思宇

* (哈尔滨工业大学航天工程系,哈尔滨 150001)

† (哈尔滨工业大学(威海)机械工程系,山东威海 264209)

引言

多体系统动力学建模与仿真对机械产品系统设计及控制具有重要的理论意义和实际应用价值[1].实际工程应用中,由于加工误差、材料属性、边界条件和外界激励等因素的影响,多体系统参数呈现不确定性的变化[2-4].研究表明在系统数学模型中忽略参数的不确定性可能会导致分析结果失去参考价值[5],如2016 年斯基亚帕雷利号(Schiaparelli)火星着陆器由于忽略了降落伞展开过程中不确定因素对系统动力学的影响,导致着陆失败[6-7].因此,开展参数不确定性对多体系统动力学特性影响规律的研究具有重要意义.

在多体系统动力学建模中,通常将不确定参数分为随机变量和区间变量[8].随机变量的分布信息由概率分布函数确定,基于蒙特卡洛方法,或多项混沌展开,可得到系统的响应统计特征[8-9],然而随机参数的样本分布信息难以获得[10].相比而言,区间分析方法采用区间变量描述参数的不确定性,只需要获得区间变量的上下边界即可,因此应用范围更广[11].

针对含区间参数的多体机械系统,扫描法[12]作为一种简单可靠的方法,能够获得系统响应的准确边界,然而该方法的计算成本随区间参数数目的增多而指数增长.基于泰勒展开,Wu 等[10]利用泰勒模型法研究了含区间参数多体系统的响应分析.由于基于泰勒展开的方法难以处理大不确定度问题,子区间技术将原区间划分为多个子区间以提高计算精度[13].为避免泰勒展开方法中的求导运算,Wu 等[10]基于切比雪夫多项式,提出了切比雪夫区间方法(Chebyshev interval method,CIM),随后该方法应用于多体系统的不确定响应分析[14-18].CIM 通过切比雪夫多项式在每个时刻近似输出响应与输入区间参数的关系,可以看作为基于代理模型的方法(surrogate based method,SBM)的一种.SBM 方法致力于构建计算成本低的代理模型,然后通过扫描法或者优化方法从代理模型获得输出响应的边界[19].基于此理念,Feng 等[11]将Legendre 多项式应用于汽车悬架系统的区间动力学响应分析,Wang 和Yang 等[3]采用任意混沌多项式研究了大炮动力系统的区间响应.此外,径向基函数[20]和克里金模型[21]也应用于区间不确定分析.陈光宋等[22]采用极大熵法获得多体系统输出参数的统计信息,进一步对分布函数采用泰勒展开获得响应区间.

然而,基于代理模型的不确定分析方法在处理长周期的区间动力学响应问题时,随着时间增大,得到的响应边界会出现恶化问题.而这种现象在概率方法和区间方法中都会出现[23-24].在多体系统中,当不确定参数取不同的值时,得到的系统响应也具有不同的频率和相位.在与时间相关的不确定动力学响应分析中,随着时间的增大,不同样本响应之间的相位差会逐渐增大,导致瞬时相位差累积效应(instantaneous phase difference accumulation,IPDA),从而使得系统响应与不确定性参数之间的关系也变得越来越复杂[24].由于这一原因,使得无论代理模型的阶数取多高,都无法在后期时刻准确近似响应函数与不确定参数的关系,从而使得随着时间的增大,得到的上下边界与实际边界存在偏差,出现边界恶化.为此,Cui 等[24]首次将自适应信号分解技术引入基于响应面法的不确定分析中,提出RS-HHT 和RS-LMD 方法,相比于传统的响应面法,该方法能够采用低阶多项式处理长时域区间不确定动力学响应问题.

在CIM 方法中,随着时间增大,样本响应间的相位差也会越来越大,此时边界的精度会随着时间的增大而降低,出现边界恶化的现象(从下文分析中可以看出).为改进CIM 方法应对长时间区间不确定分析中出现的边界恶化现象,本文将信号分解技术与切比雪夫多项式结合,采用切比雪夫多项式分别对HHT 变换(Hilbert-Huang transform,HHT)和局域均值分解(local mean decomposition,LMD)得到的瞬时幅值和瞬时相位近似,提出CIM-HHT 方法和CIM-LMD 方法.该方法将动力学响应分解为多个具有各自振幅和相位的单分量和一个残差分量,基于切比雪夫多项式对每个单组分响应和残差分量构建相应的代理模型,并得到系统的耦合代理模型.最后,以典型的单摆和曲柄滑块机构为例,考虑模型中的参数不确定性,验证了CIM-HHT 和CIM-LMD 方法的有效性.

1 多体系统的切比雪夫区间方法

1.1 含区间参数的多体系统动力学建模

通常,不考虑参数的不确定性时,多体系统的动力学特性可由一组微分代数方程描述

式中,q为系统广义坐标矢量,M为系统质量矩阵,Q为包含重力,弹性力等的广义外力矢量.Φ 为约束方程,Φq为约束方程的雅可比矩阵,由 Φ对q求偏导获得,λ 为拉格朗日乘子.

实际工程应用中由于生产工艺,外界环境等影响,物理系统的参数往往呈现不确定性.当采用区间模型描述参数的不确定性时,不确定参数的变化由区间的上下边界限制,此时只需获得参数的上下边界信息即可.考虑物理系统中的不确定参数由一组区间矢量定义,如下式

此时区间微分代数方程的解可由一组集合描述

由于式(3)的精确解集合往往呈现非凸流形,往往采用精确解集的最小超立方近对其近似[25],此时,区间方程的响应可由相应的区间边界表达

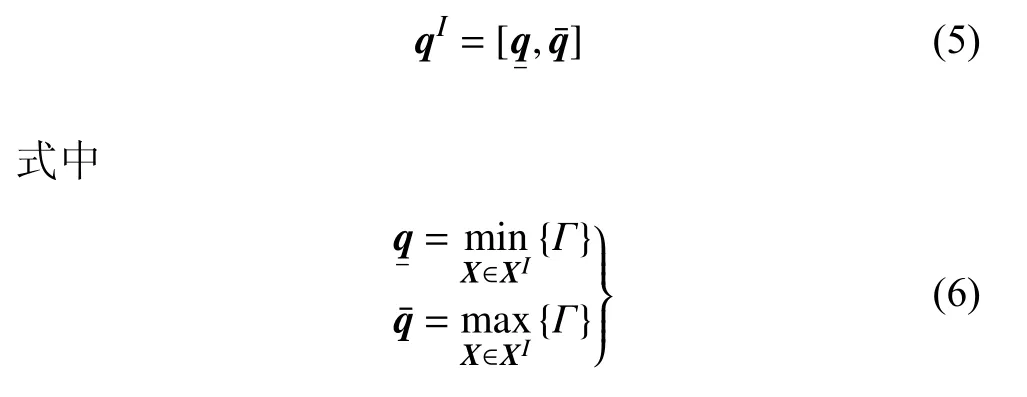
1.2 切比雪夫区间方法

Wu 等[10]首先基于切比雪夫多项式提出切比雪夫区间方法(CIM),作为一种非嵌入式方法,该方法已广泛应用于多体系统的区间不确定量化[26-28].根据Weierstrass 理论,定义在区间[a,b]上的实值连续函数可由多项式近似,而切比雪夫多项式具有最佳展开多项式之称.对于一维问题,定义在[a,b]上的p阶切比雪夫级数为

式中,变量x∈[a,b] 且 θ ∈[0,π] .

则单变量连续函数f(x)∈[a,b] 可近似为

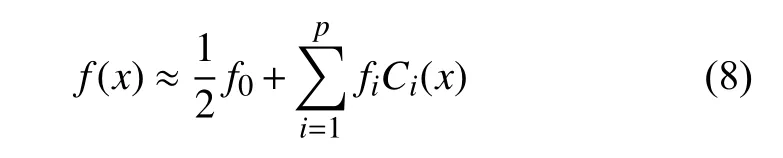
式中,fi为多项式的系数.

对多维问题,切比雪夫多项式是每个一维多项式的张量积.k维切比雪夫多项式定义为

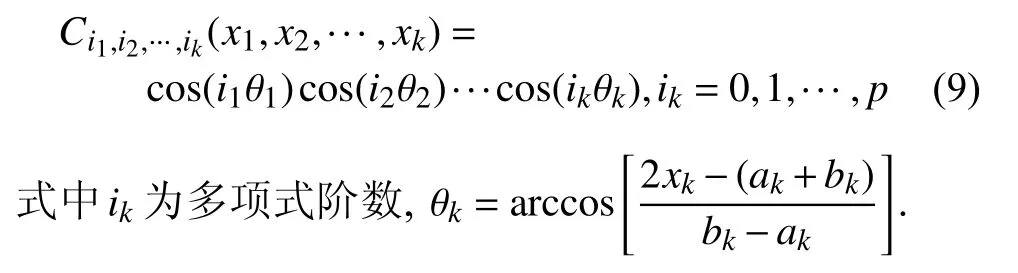
此时,多维函数f(x)=f(x1,x2,...,xk) 可以由n阶切比雪夫多项式近似为

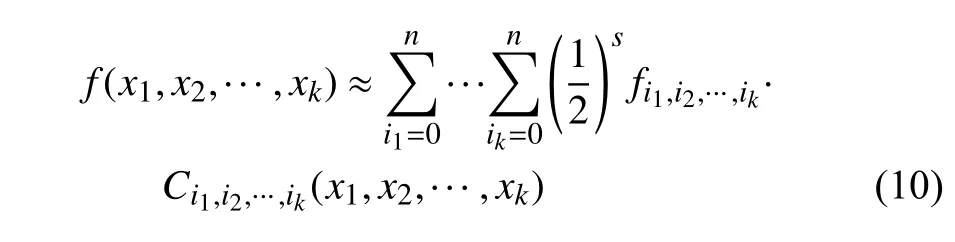
式中,s为下标i1,i2,···,ik中零的数目.

此时,切比雪夫多项式的系数可由Mehler 积分得到

式中,m为多项式插值点数,一般为保证近似精度,取m=p+1.

至此,可通过切比雪夫多项式构建响应函数的代理模型,对构建的代理模型运用扫描法可得到系统输出响应的上下边界.

2 基于信号分解的切比雪夫区间方法

2.1 希尔伯特-黄分解

希尔伯特-黄变换[29]包含两个步骤,经验模态分解(empirical mode decomposition,EMD) 和Hilbert 变换(HT).EMD 的基本理念为将一个信号分解为多个本征模函数(intrinsic mode functions,IMFs)之和,进一步采用HT 变换可得到每个IMF 对应的瞬时幅值(instantaneous amplitude,IA)和瞬时相位(instantaneous phase,IP).

对于初始的信号x(t),EMD 的分解步骤如下:

(1) 取初始残差信号ri(t) 等于初始信号x(t),并使hi j(t) 与ri(t) 相等.其中i为IMF 的个数,j为对应第i个IMF 的筛选次数.初始时,i和j都为0.

(2) 识别并提取hi j(t) 所有的局部极大值和极小值.

(3) 在局部极小值点和极大值点上基于三次样条插值得到极值的上包络线emax(t) 和下包络线emin(t),定义上下包络的均值为

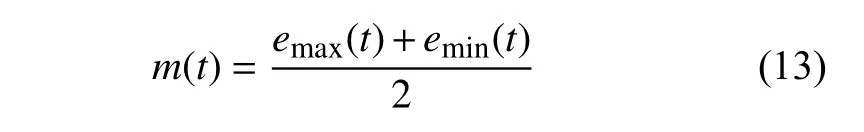
(4) 从hi j(t) 分离出m(t),并将结果赋值给hij(t),有

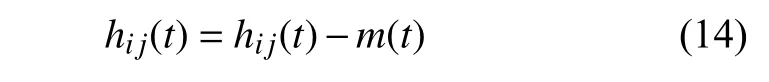
(5) 重复步骤(2)～(4),直至hi j(t) 的均值为零,筛选过程的终止准则为

(6) 当筛选准则满足时,将最终的hi j(t) 构建为一个本征模态函数ci(t),即

(7) 计算新的残差信号ri(t)

(8) 将残差ri(t) 赋值给新的hi j(t) .重复上述分解步骤(2)～(7),直至分解停止准则满足.取迭代步数为n,通过EMD 分解,信号x(t) 可分解为

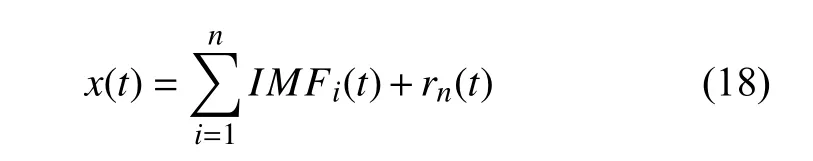
从上述步骤可以看出,EMD 包含内循环和外循环两个循环,内循环为筛选过程,外循环为分解迭代过程.此外,可将最大的IMFs 个数作为分解停止准则,将最大的移位过程个数作为筛选终止准则.

进一步,对每个IMF采用希尔伯特变换(HT)可获得瞬时幅值IA 和瞬时相位IP[30],对于信号y(t),其HT 变换定义为

式中,H(·) 为HT 函数.此时,信号z(t) 为

可以看出,z(t) 的实数部分为原始信号y(t),虚数部分为HT 变换得到的虚信号.

此时,信号x(t) 可以通过HHT 分解为

2.2 局部均值分解

局域均值分解(local mean decomposition,LMD)将单一信号分解为几个积函数(product functions,PFs)之和,每个积函数为一个包络信号和一个纯调频信号的乘积[31-32].对于初始信号x(t),LMD 的主要步骤如下:

(1) 取x(t) 为初始残差信号ui(t),并使sij(t)=ui(t) .其中i为PF 的数目,j为第i个PF对应的筛选次数.初始筛选时,i和j都为0.

(2) 确定sij(t) 的所有极值ni jk,其中k表示所有极值中的第k个极值.对两个连续的极值ni jk和ni j(k+1),第k段的局域均值mi j(t) 为

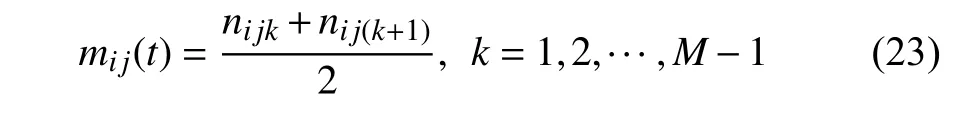
式中,M为极值的总数.两个连续极值ni jk和ni j(k+1)之间第k段的局部幅值ai j(t) 为

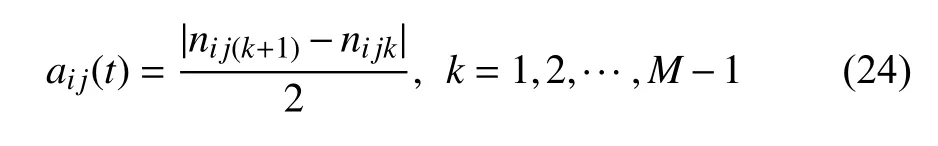
(3) 采用滑动平均法(moving average method)[31]对mi j(t) 和ai j(t) 进行滑动平均,直到任何相邻点不再相等,其中滑动平均法的步长为mi j(t)或ai j(t) 的最大步长的三分之一.

(4) 从sij(t) 中 分离出mi j(t) 并 将结果赋值给hi j(t),即

再将ai j(t) 除以hi j(t) 并将结果赋值给sij(t)

(5) 重复上述筛选过程(2)～(4),直至sij(t) 为纯调频信号,相应的筛选终止准则为

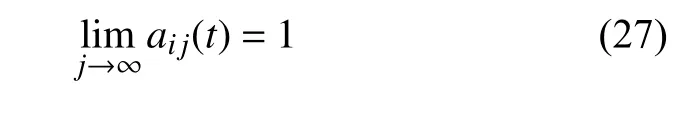
(6) 筛选过程终止后,第i次筛选结束时,假设此时j取值为li,则第i个PF的IA 为

第i个PF的IP 为

则第i个PF可写为

(7) 计算残差信号

(8) 将新的残差信号ui(t) 作为新的sij(t),重复上述筛选过程(2)～(7),直至满足分解终止准则,此时,原始信号可分解为

注意到HHT 和LMD 都基于原始信号的极值进行分量筛选,因此当原始信号的端点不是极值点时,会使得分解得到的结果产生偏差,即末端效应.本文采用镜像延拓法[33]以减弱HHT 和LMD 筛选过程中的末端效应.

2.3 CIM-HHT 方法和CIM-LMD 方法

信号分解的方法可以将一个多分量信号分解为多个单分量分信号,HHT 和LMD 分解只作用于信号本身,因此可以应用于区间不确定分析.本文将HHT 和LMD 分解策略与CIM 结合,提出CIMHHT 和CIM-LMD 两种方法,以解决CIM 方法在求解含区间参数动力学响应边界中面临的边界退化问题.CIM-HHT 和CIM-LMD 的主要步骤如下:

(1) 根据CIM 方法,生成区间不确定参数X的样本点,代入确定性DAE 求解器得到每个样本点对应的响应;

(2) 对每个样本响应在每个时间步长上进行HHT 和LMD 分解,得到m个单组分响应cj和一个残差r(t) .每个单组分响应可以由瞬时相位和瞬时幅值的和近似

(3) 每个样本响应分解得到的每个瞬时幅值(IA),瞬时相位(IP)和残差,基于切比雪夫多项式构造代理模型

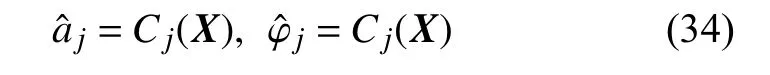
式中,C(·) 表示构建切比雪夫代理模型的过程.

CIM-HHT 方法和CIM-LMD 方法的计算流程如图1 所示.

图1 CIM-HHT 和CIM-LMD 计算流程Fig.1 Flowchart for CIM-HHT and CIM-LMD

3 算例分析

3.1 算例1:单摆

本节以刚性摆为例,对CIM-HHT 和CIMLMD 进行长周期区间分析的有效性进行验证.刚性摆如图2 所示,单摆在重力作用下由初始角度释放.单摆长度为1.8 m,初始释放角度为 π/3 .

图2 单摆Fig.2 Simple pendulum

考虑单摆长度的不确定性,对单摆末端点的位移响应进行仿真.其中单摆长度区间不确定度为5%,仿真时间50 s.为验证本文方法的有效性,采用扫描法和切比雪夫区间方法进行对比,其中扫描点数为100,切比雪夫多项式的阶数为4.

采用HHT 和LMD 对不确定参数取中点处的值时,对末端点x方向的位移和速度进行分解,得到的结果如图3 所示.可以看出HHT 和LMD 将位移响应和速度响应分解为1 个单分量和1 个残差分量之和,两种分解方法得到的瞬时相位保持一致,且都呈现单调递增的特性.相比之下,HHT 得到的瞬时幅值呈现上下振荡的特点,而LMD 得到的瞬时幅值变化很小,基本保持不变.由于末端效应的影响,HHT 得到的瞬时幅值在两端波动较为剧烈,可见LMD 末端效应较HHT 更弱.

图3 末端位置和速度的HHT 和LMD 分解Fig.3 HHT and LMD decomposition of position and velocity response of end-tip

为研究不同样本下系统响应的HHT 分解和LMD 分解特性,图4 给出了第1、第3 和第5 个切比雪夫多项式零点处的末端位置响应分解.从图中可以看出,不同样本响应下,HHT 得到的瞬时幅值振荡,各个分量之间存在相位差,而LMD 分解得到的瞬时幅值基本保持不变,此时基于LMD 分解构建的代理模型也更为准确.

图4 不同样本的末端位置响应分解Fig.4 Decomposition of position response of end tip under different samples

图5 给出了末端位置x方向的响应上下边界.显然,随着时间的增大,CIM 得到的边界精度逐渐降低,这是由于不同样本的相位差产生的IPDA 效应造成的.CIM-HHT 与扫描法得到的边界则较为接近,CIM-LMD 得到的边界与扫描法得到边界则基本一致.同时,相比LMD,HHT 的末端效应更为明显,这也反映在CIM-HHT 获得的区间边界上.通过引入信号分解技术,可避免CIM 方法在长周期区间动力学响应分析中产生的边界恶化问题.

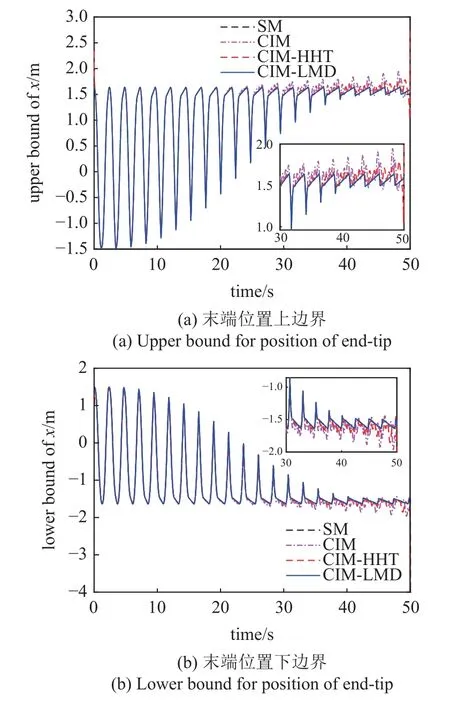
图5 末端位置响应边界Fig.5 Bounds for position responses of end-tip

图6 给出了末端点x方向的速度响应的上下边界.与图5 中的结论类似,相比CIM,CIM-HHT 和CIM-LMD 能够在长周期区间分析中得到更准确的结果.此外,在速度响应中,相比位置响应,随着时间的增大,CIM 方法产生的区间恶化更为剧烈,这与响应与不确定参数的关系有关.当响应的非线性越强时,随着时间的增大,样本响应产生的IPDA 效应越强,CIM 得到的边界精度越低.从图6 中可以看出,CIM-LMD 对IPDA 效应抑制效果更好,得到的结果与扫描法的结果基本一致.

图6 末端速度响应边界Fig.6 Bounds for velocity responses of end-tip

进一步,将本文方法与文献[24]中的方法进行比较,图7 为由RS-HHT 和RS-LMD 得到的末端位置的响应边界.从图7(a)中可以看出,与RS-HHT 得到的响应边界相比,CIM-HHT 得到的响应边界更为保守.由于HHT 分解得到的瞬时幅值随时间振荡,且不同样本响应的瞬时幅值之间存在相位差,使得响应的瞬时幅值与不确定参数之间的关系随着时间增长越来越复杂,采用切比雪夫多项式对瞬时幅值的逼近精度较高,因此CIM-HHT 得到的边界更为保守.而在图7(b)中,CIM-LMD 和RS-LMD 得到的响应边界基本一致.由于LMD 分解得到的位置响应的瞬时幅值基本保持不变,此时瞬时幅值相对于不确定参数的关系呈现弱非线性,RS 和CIM 都能获得理想的近似精度,两种方法得到的响应边界基本一致.

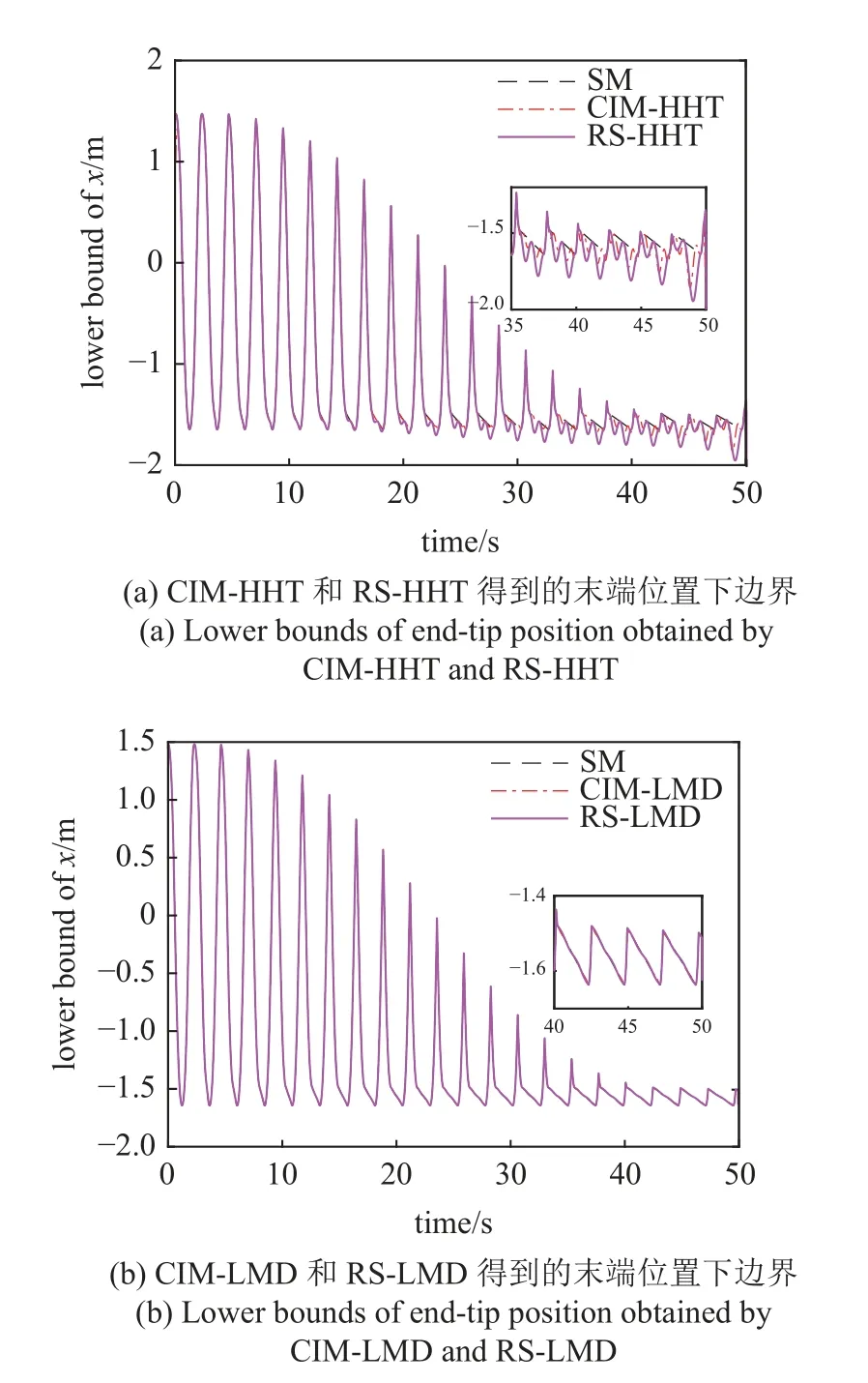
图7 不同方法得到的位置响应边界Fig.7 Bounds for position responses of end-tip obtained by different methods

3.2 算例2:曲柄滑块机构

为进一步验证CIM-HHT 和CIM-LMD 方法对非线性响应边界获取的有效性,以曲柄滑块机构为例,如图8 所示研究CIM-HHT 和CIM-LMD 分析曲柄滑块机构的长周期区间响应.曲柄机构的参数如表1 所示.

图8 曲柄滑块机构示意图Fig.8 Schematic diagram for crank slider

表1 曲柄机构参数Table 1 Parameters for crank slider

考虑曲柄长度的参数不确定性,此时L1为区间数=L1(1±1%) .仿真时间6 s,其中扫描法样本点数为50,切比雪夫多项式阶数为4.

图9 为在不确定性参数取中点处的值时,对滑块速度和位移响应的HHT 和LMD 分解结果.由图可知,HHT 和LMD 将滑块位置和速度响应分解为1 个单分量和1 个残差分量.图9(a) 中可以看出,HHT 分解得到的瞬时幅值上下波动,而LMD 分解得的瞬时幅值基本保持不变.在图9(b)中,LMD 分解得到的瞬时幅值单调变化,而HHT 得到是瞬时幅值上下振荡,且越来越剧烈.

图9 滑块位移和速度响应的HHT 和LMD 分解Fig.9 HHT and LMD decomposition for position and velocity response of slider

图10 给出了考虑区间不确定参数的滑块位移响应的上下边界.从t=2 s 后,随着时间的增大,由于IPDA 效应,CIM 得到上下边界精度越来越低.CIM-HHT 和CIM-LMD 则能够保持较好的精度,CIM-LMD 获得的边界与参考值基本一致,且具有更弱的末端效应,说明CIM-LMD 能够更好地应用于长时间区间动力学响应分析.

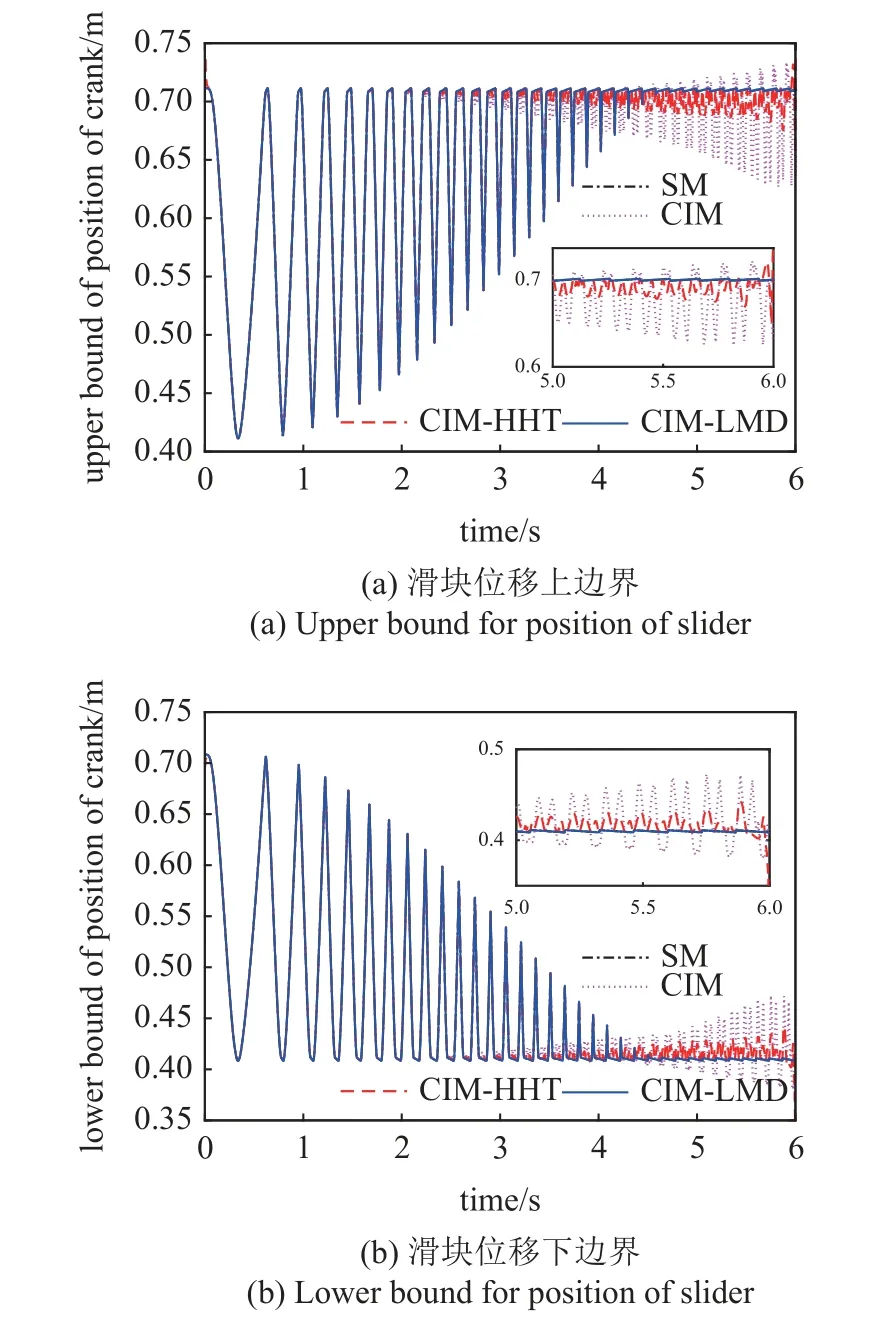
图10 滑块位移响应边界Fig.10 Bounds for position response of slider

滑块速度响应的上边界如图11 所示,可以看出CIM-HHT 得到的上边界随时间增大也出现了精度降低,这与HHT 分解得到的瞬时相位相关.如图9(b)所示,HHT 分解得到的瞬时相位振荡剧烈,而LMD分解得到的瞬时相位单调变化.相比位移响应,滑块速度响应具有更强的非线性,此时,CIM-LMD 能够获得更准确的数据.

图11 滑块速度上边界Fig.11 Bounds for position responses of slider

图12 为曲柄角度上下边界随时间变化趋势.显然,CIM,CIM-HHT 和CIM-LMD 得到的结果与扫描法得到的结果吻合较好,这是因为曲柄转角响应为单调变化,样本响应间不存在IPDA 效应,因此在长周期区间分析中CIM 能够获得准确的结果.

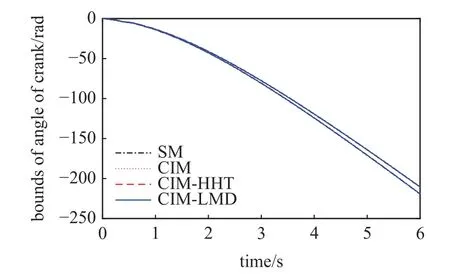
图12 曲柄角度边界Fig.12 Bounds for angle of crank

曲柄角速度响应边界如图13 所示,在CIMHHT 和CIM-LMD 中,不确定参数的每个样本响应由HHT 和LMD 分解为2 个单分量响应和1 个残差分量.从图中可知,随着时间增大,在t=2.5 s 之后,CIM 得到边界精度越来越低,而CIM-HHT 和CIMLMD 能够保持较好的计算精度.在仿真初期和末期,由于末端效应,CIM-HHT 和CIM-LMD 与扫描法的结果存在微小的偏差.注意到CIM-HHT 在t在0～1 s 之间的结果产生的偏差更大,这是由于HHT 分解中的模态混叠导致的[34].

图13 曲柄角速度边界Fig.13 Bounds for angular velocity of crank

进一步,图14 给出了RS-HHT 和RS-LMD 方法得到的滑块速度响应下边界.由图可知,RSLMD 和CIM-LMD 得到的响应边界曲线基本一致,而CIM-HHT 相比RS-HHT,得到的响应边界随着时间增长边界恶化效应减弱,与算例1 中图7 得到的结论一致.

图14 不同方法得到的滑块速度响应边界Fig.14 Bounds for response of slider velocity using different methods

为了进一步说明本文方法的有效性,考虑曲柄长度和质量在区间内变化,参数不确定度为5%,此时有

采用RS-LMD 和CIM-LMD 计算系统的响应边界,在RS-LMD 和CIM-LMD 中多项式的阶数均为2,对代理模型的扫描样本数为50,仿真计算结果如图15 所示.由图可知,CIM-LMD 得到的响应边界与参考边界基本一致,相比之下,RS-LMD 得到的响应边界存在一定的偏差.其原因在于,在RS-LMD 中瞬时幅值、瞬时相位和残差的耦合代理模型基于泰勒多项式构建,而在CIM-LMD 中基于切比雪夫多项式构建耦合代理模型.由于泰勒多项式为局部近似,而切比雪夫多项式在整个区间上一致近似[35],因此当参数不确定度增大时,CIM-LMD 对瞬时幅值、瞬时相位和残差的逼近更准确,从而能够获得更准确的耦合代理模型,得到的响应边界更为保守.

图15 不确定度为5%时CIM-LMD 和RS-LMD 得到的响应边界Fig.15 Bounds of responses using CIM-LMD and RS-LMD under 5% uncertainty level

4 结论

针对传统的切比雪夫方法在处理多体系统长周期区间动力学响应边界计算时出现的边界恶化问题,本文提出了基于信号分解技术的CIM-HHT 和CIM-LMD 方法.HHT 和LMD 能够将系统响应分解为多个单分量响应之和,对每个单分量的幅值和相位基于切比雪夫多项式构建代理模型,进一步得到系统的响应边界.通过数值算例研究,得到以下结论.

(1) CIM-HHT 和CIM-LMD 能够将非线性、非平稳响应分解为多个弱线型、单分量响应之和,适用于含区间不确定性多体系统长周期动力响应分析.

(2)相比CIM,CIM-HHT 和CIM-LMD 能够在一定程度上改进CIM 方法由于响应相位差累积导致的边界精度下降问题.

(3)相比CIM-HHT,CIM-LMD 具有更弱的末端效应,更平稳的分解过程,在多体系统区间不确定分析中计算精度更高.