一类面向高阶精度自适应流动计算的流场插值方法1)

周 帅 肖周芳 付 琳 汪丁顺

* (中国航空发动机研究院,北京 101300)

† (杭州电子科技大学计算机学院,杭州 310018)

引言

随着计算机软硬件技术的发展,以计算流体力学(computational fluid dynamics,CFD)为核心的数值模拟技术已成为空气动力学领域工程与科学问题分析中一项不可或缺的工具[1].然而,针对复杂几何外形和复杂流动问题,CFD 计算仍然面临求解精度和效率的挑战[2].网格自适应技术[2-8]和高阶精度数值方法[9-14]的结合有望提升CFD 复杂问题适应能力,还可在更少的网格上获得更快的渐进收敛速度[2,10].然而,这两项技术却并未在主流商业CFD 软件中使用.这主要是由于网格自适应技术涉及诸多环节的协同工作,其还存在鲁棒性问题,并且要将这两项技术结合还需要解决一系列技术难题[2].其中一个难题便是如何将前一自适应迭代步中的计算结果高精度地插值到后一迭代步的自适应更新网格中,这一个过程称为物理量插值.

物理量插值又被称为物理量转移或物理量重映[15-25],是将物理量从一网格上转移到另一网格上,其常被应用于网格变形[16-19]和网格自适应更新[15]等计算问题中.在自适应流场计算中,通过物理量插值可使当前流场计算延续上一迭代步中的计算状态,从而加速流场计算的收敛速度[20-21].该过程中需关注物理量守恒和插值精度等特性.前者将物理量在从背景网格单元转移到新网格单元上后,需保持物理量的守恒;对于后者,物理量的插值精度应和当前采用的数值方法精度一致.

以上物理量插值的两个特性对于提升整个自适应流场计算流程的稳定性具有重要的作用[21],尤其在非定常流动计算中,由物理量插值导致的数值误差会累积到之后的流动计算中.简单的线性插值算法无法满足物理量守恒特性,且其只能达到一阶插值精度.文献[15]提出了针对二维非结构网格的满足物理量守恒及二阶精度的物理量插值算法,物理守恒通过局部网格相交运算实现,二阶精度通过重构物理量梯度实现.随后,Alauzet[22]继续将该物理量插值算法拓展到了三维非结构网格上.文献[17,23]采用基于ENO 方法实现物理守恒的物理插值方法,文献[23]在二维网格上实现了三阶精度的物理量插值.针对二维四边形网格物理量插值问题,Lei 等[24]发展了基于WENO 的高精度插值方法.Zhang 等[25]针对高阶间断伽辽金(DG)数值解在变形网格和移动网格应用中的物理量插值需求,设计了DG 插值方法,实现了守恒和高阶的物理量插值.

本文提出一类满足物理量守恒和高精度的物理量插值方法,以适应高阶精度自适应流动计算.为实现流场插值过程中物理量守恒,该方法先计算新旧网格的重叠区域,然后将物理量从重叠区域的旧网格转移到新网格中.为满足高阶精度要求,先采用kexact 最小二乘方法[26]对旧网格上的数值解进行重构，得到满足精度要求的物理量分布多项式,随后采用高斯数值积分实现物理量精确地转移到新网格的各单元上.本文算法有助于推进网格自适应技术和高阶精度数值方法的结合,从而提升CFD 复杂问题适应能力.

1 算法流程

考虑二维自适应流动计算,记Mnew为前迭代步网格(也称为新网格),Mback为上一迭代步中的网格(也称为背景网格),本文算法目的为将分布在Mback上的物理量插值到Mnew中,使得插值后的解具有(r+1)阶精度并满足在插值过程中物理量守恒.为实现上述目的,本文算法步骤如下.

(1) 物理量重构:针对Mback中的每个网格单元,构建描述流场物理量在该单元中分布的r次多项式表达式U(x,y).

(2) 网格相交计算:利用Mback中的网格边将Mnew中的每个网格单元分割得到多个子单元,这些子单元为Mnew中对应单元与Mback中不同网格单元的重叠部分.

(3) 物理量转移:针对Mnew中的每个网格单元,根据分布于Mback上的流场物理量U(x,y)累积分布于该单元对应子单元上的物理量,累积结果作为该单元上的物理量总量,并以该单元单位面积上的物理量为其参考点上的物理量值.

上述步骤中,步骤1 和步骤3 是实现高阶精度流场物理量插值的关键.其中,步骤1 用于将背景网格上的物理量重构为r阶精度,步骤3 用于确保物理量转移到新网格后保持r阶精度,将在第2 节和第3 节分别讨论这两部分内容.步骤2 中分割后的子单元用于实现插值过程中物理量守恒,其中涉及网格求交计算较为成熟[27-29],本文不再赘述.特别地,本文对在二维非结构三角形网格间插值进行阐述,其思想同样适用于三维非结构四面体网格.

2 物理量重构

本文采用应用于有限体积法中的k-exact 最小二乘法[26]进行旧网格上的物理量重构.为了完整性,将结合本文中的流场插值需求,简述该算法过程.物理量重构的目的为针对背景网格Mback上的任一网格单元i,构建关于该单元参考点的物理量分布r次多项式

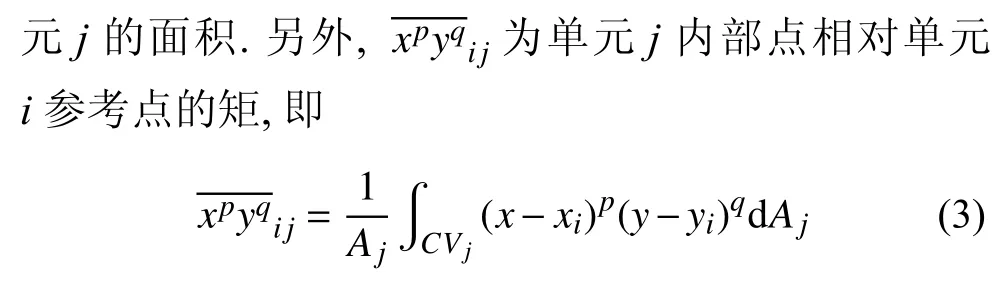
该式的计算仅跟网格几何位置相关,关于其计算方法请参考文献[26].

从式(1)和式(2)可知,在二维情形中,次数为r的多项式含有(r+1)(r+2)/2 个未知项系数.为求解这些未知项,需选择(r+1)(r+2)/2 个单元i的邻接单元并针对每个单元建立一个如式(2)的等式.在实践中,通常选择多于(r+1)(r+2)/2 个邻接单元构建方程数多于未知项数的方程组[24],这些邻接单元被称为单元i的重构模板.随后,采用最小二乘法求解这些未知项,即式(1)中的多项式系数.

3 流场插值

3.1 满足物理量守恒的插值

在自适应流动计算中,不同迭代步的网格通常相互独立.不失一般性,本文考虑相互独立的网格间的物理量插值情形.如图1(a)所示,黑色边表示的网格为Mback,红边表示的网格为Mnew(为便于展示,此处只以部分网格单元示意这两套网格).图1(b)展示网格相交计算后获得Mnew中网格单元△ABC对应的子单元结果,共有4 个子单元,分别为与Mback中三个单元重叠的区域.

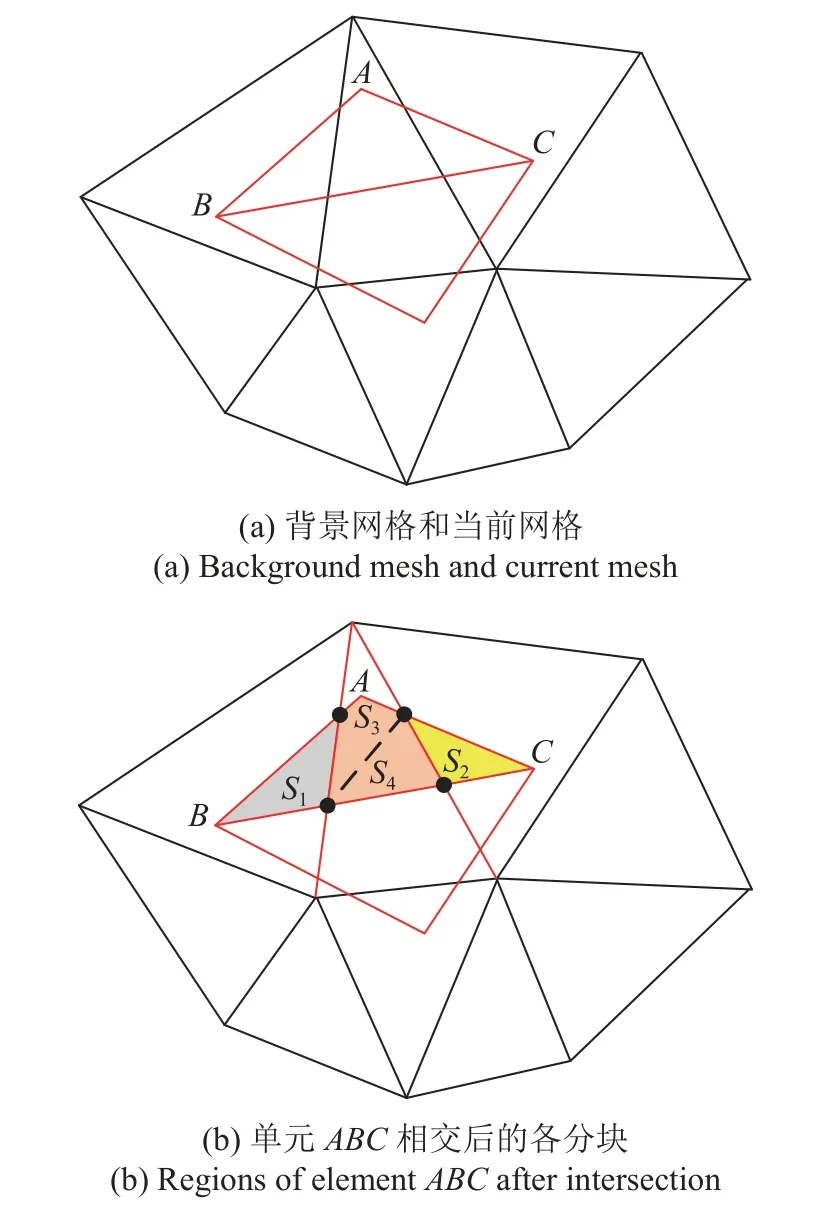
图1 二维物理量守恒插值示意图,背景网格和当前网格分别用黑边和红边表示Fig.1 Schematic diagram of two-dimensional conservation of physical quantity interpolation,the background mesh and the current mes are represented by red and black edges respectively

3.2 高阶精度插值

从式(4)可知,为求解Mnew中网格单元内的物理量需进行体积分计算,该计算的精度将影响最终的流场插值精度.为获得高精度积分结果,本文采用高斯积分求解式(4)右端的积分项,即

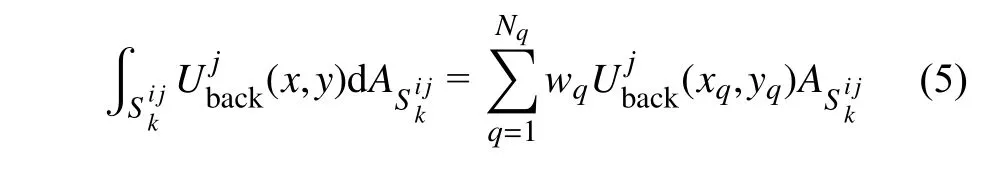
式中,Nq为高斯积分点个数,(xq,yq)为积分点坐标,wq为对应该积分点的权重.注意,高斯数值积分的精度和采用的高斯积分点个数相关.为此,针对不同的精度要求,需采用不同的积分点数及相应的积分点坐标和积分点权重.

为支持高阶精度的流场插值,针对积分区域为三角形情形,采用文献[26,30]中推荐的高斯积分点信息.表1 展示了针对2～ 4 阶精度被积函数所采用的高斯积分点数、坐标和相应权重.注意,表1 中所列的积分点坐标为其重心坐标.当所采用的流场数值计算方法精度高于4 阶时,需采用更多的高斯积分点数.

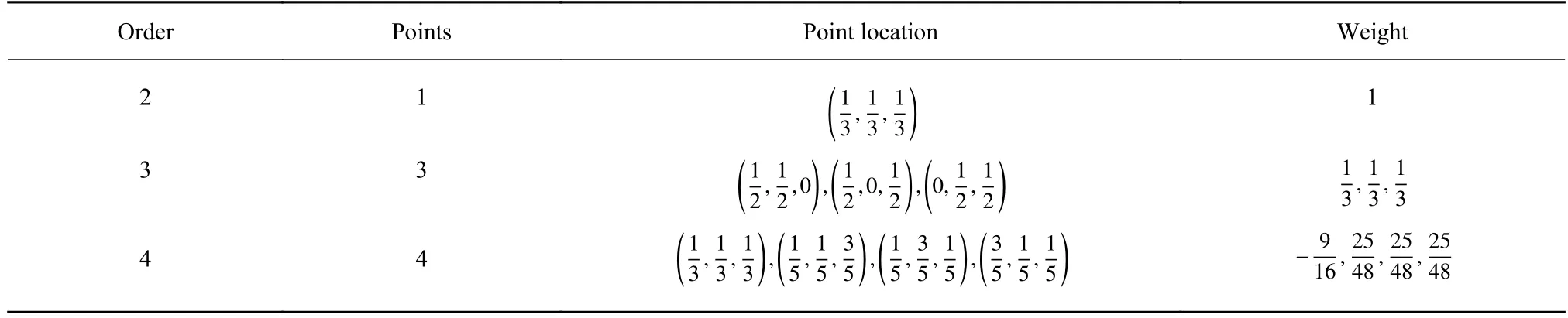
表1 不同阶数精度对应的积分点信息Table 1 Information of integration points corresponding to different order

4 数值实验

选用两个例子测试本文提出的面向高阶自适应流动计算的流场插值方法,第一个例子通过具有解析解的流场验证该算法的插值误差,第二个例子则将该算法应用于高阶自适应流动计算中.文中所有测试例子均在小型工作站上运行,计算机配置为,内存容量:16 GB;CPU 型号:六核Inter Core i7-8700,主频:3.2 GHz.

4.1 圆环模型

该模型为四分之一圆环模型[26],圆环内圆半径为2、外圆半径为3 (如图2 和图3 所示).考虑非黏性超音速涡流流经该模型,流场边界条件为:内圆边界为入口边界,在此处的马赫数为Mi=2、质量密度ρi=1.区域其他位置的流场变量(密度ρ、速度分量u、速度分量v和压力P)值由以下式子定义

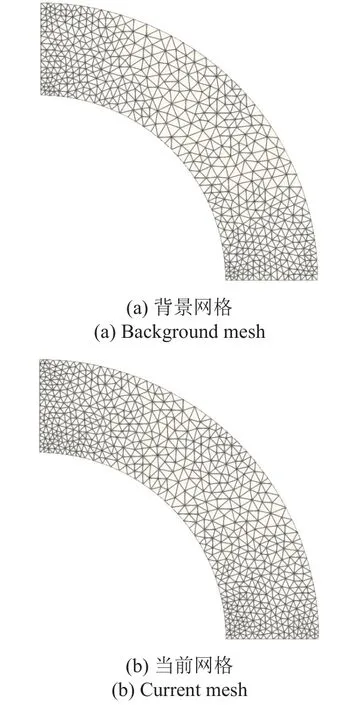
图2 第一组网格Fig.2 The first group of meshes

图3 第二组网格Fig.3 The second group of meshes

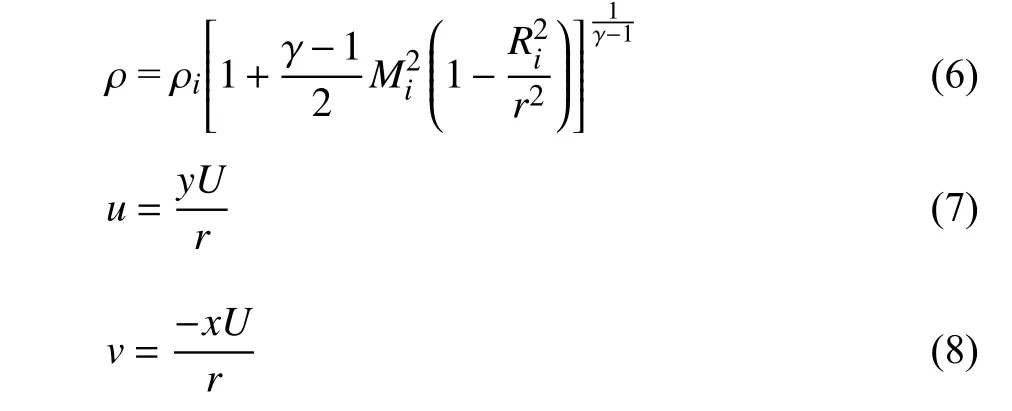
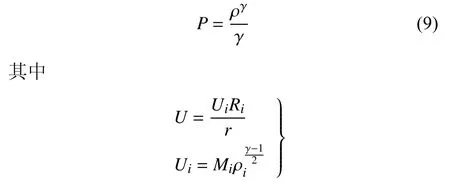
在自适应流场计算中,为延续上一迭代步的计算状态,需要在每一迭代步开始前执行流场插值过程,以获得该迭代步的初始解.本文模仿自适应流场计算过程中的插值过程,即将定义在一套网格(背景网格)中的流场插值到另一套网格(当前网格)中,不同的是此处定义在背景网格上的流场通过流场变量的解析式(6)～ 式(9)求出.为验证本文插值算法的精度,除了从背景网格上获得的插值解之外,在新网格上也通过流场变量的解析式计算精确解.随后,针对每一个新网格上的网格单元,根据以下式子计算插值误差

式中,φExact和 φi分别表示在该单元上基于精确值和流场插值得到的单位面积上的物理量值.

为实现上述插值误差计算,设置两组不同规模的网格,每组网格由两套网格组成,分别为背景网格和当前网格,且背景网格的网格单元数比当前网格单元数少.图2 和图3 分别展示了这两组网格,表2显示了这两组不同规模网格的网格单元数和网格点数,第二组网格的规模大于第一组网格的规模.表3展示了在不同插值精度情形下在这两组不同规模的网格上得到的插值误差的L1范数、L2范数和L∞范数.从表中数据可知,当网格规模相同时,插值精度阶数越高,插值误差越小;当插值精度相同时,网格规模越大,插值误差越小.

表2 两组不同规模的网格数据Table 2 Two groups of meshes with different scales

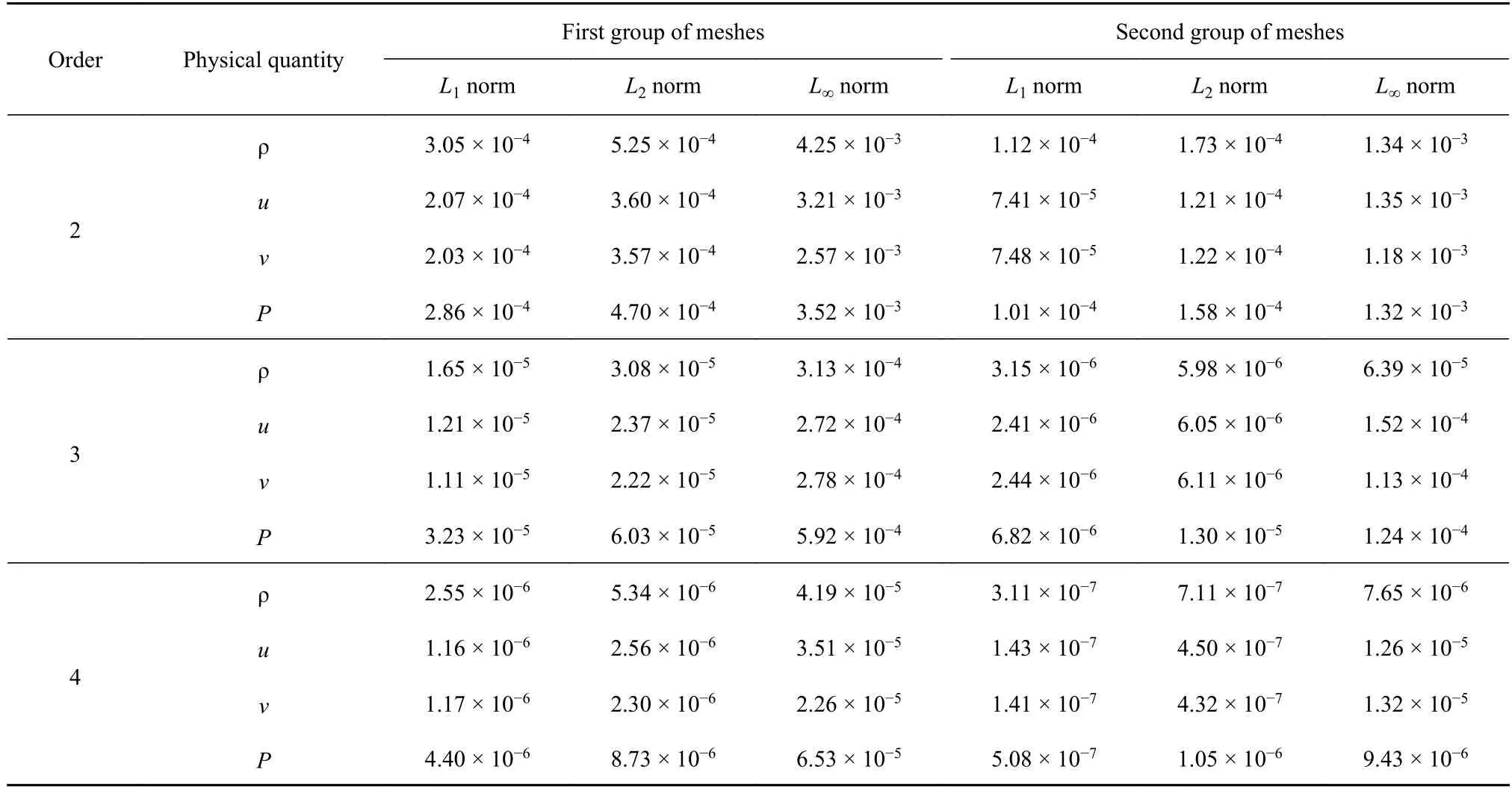
表3 在不同网格规模和不同插值精度下的流场插值误差Table 3 Interpolation errors of flow field under different mesh scales and different orders of interpolation accuracy

4.2 NACA 0012 模型

以NACA 0012 翼型外流场数值计算为例验证本文插值方法在自适应流动计算中的有效性.该翼型外流场的计算条件为:雷诺数Re=5000,马赫数Ma=0.5 和攻角a=0.为获得该流场数值解,采用3 阶精度的高阶流场求解器进行自适应迭代求解.图4(a)中的网格为初始计算网格,由7790 个网格单元和3966 个网格点组成.该初始网格在翼型附近区域分布较稀疏(见网格放大图),难以捕捉翼型附近区域的精细流场特征.为此,采用自适应技术根据流场解更新计算域网格,并基于新的网格重新计算流场数值解.

本文采用文献[31-32]中的方法根据流场解计算用于更新网格的单元尺寸场,并采用局部操作技术更新网格.最终,通过6 次自适应迭代获得收敛的流场数值解.图4(b)～图4(d)展示了前四次自适应迭代计算的网格,可以发现随着自适应迭代次数的增加,翼型附近区域和尾迹区的网格越来越密,因此网格单元数和网格点数也不断增加(见表3).图5 展示了自适应计算收敛过程中气动系数(升力系数和阻力系数)随网格规模变化的变化.最终,升力系数值收敛于0.000572(理想值为0);阻力系数收敛的值为0.0555,这和文献[33]中展示的基于多种网格计算得到的阻力系数值接近.图6 展示了自适应迭代收敛后的马赫数分布图,可以发现在翼型附近区域和尾迹区具有清晰的流场特征.

图4 翼型计算域在不同自适应计算迭代步中的网格Fig.4 Meshes of the airfoil computational domain in different adaptive computation iteration steps

图5 自适应计算收敛过程中气动系数随网格规模变化的变化Fig.5 Convergence of lift and drag coefficients against degrees of freedom (vertices)

图6 自适应迭代收敛后的马赫数分布图Fig.6 The distribution of Mach number after adaptive solution convergences

本文流场插值方法已集成于上述所采用的高阶流场求解器中,为说明该插值方法在自适应流场计算中的作用,对比有流场插值功能和无流场插值功能时,求解器在每一自适应迭代步中的求解收敛情况.在每一次自适应计算中,需要在新网格上重新求解流场控制方程,该求解过程最终转化为线性方程组的迭代求解,求解收敛条件为残差小于给定门限值(本文中采用的值为1.0 × 10−9).在无流场插值步骤时,每次自适应计算从给定初始值开始进行流场控制方程求解;而在有流场插值步骤时,自适应计算则以上一次计算结果插值到当前网格后的解作为初始计算条件从而延续上一次自适应计算状态.

表4 展示了在分别有流场插值和无流场插值步骤时,每一次自适应计算收敛迭代步数和收敛时间.因为可以延续上一次计算状态,流场插值功能可以有效缩短在新网格上的收敛迭代步数,从而缩短收敛时间.如在第一次自适应计算时,无流场插值步骤时,求解器需要15 迭代步来求解流场控制方程;而在有流场插值步骤时求解迭代步缩短到11 步,收敛时间从40.1 s 降到33 s,加速比为1.22.随着自适应次数的增加,网格规模越来越大,所需的数值求解时间也增多.从表中数据可知,当网格规模越大时,流场插值功能在提高收敛速度方面效果越明显.如在第6 次自适应迭代计算中,当添加流场插值功能后,收敛迭代步数从29 步降低到10 步,收敛时间从294.6 s 降低到125.3 s,收敛加速比为2.35.需要说明的是,在本算例中,不管是否有流场插值功能,每一次自适应迭代计算都收敛到相同的结果.

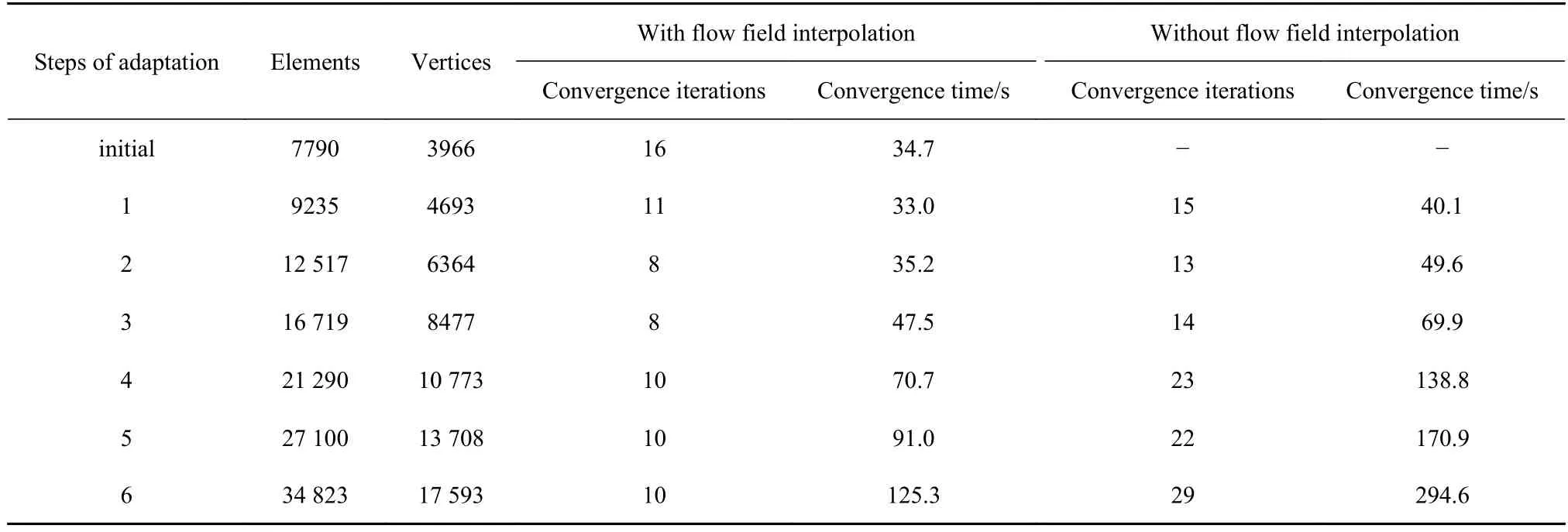
表4 有无流场插值功能时求解收敛情况Table 4 Convergence of solution with or without the flow field interpolation

5 结论

本文提出了一类高精度流场插值方法,实现将前一迭代步网格中流场数值解插值到当前迭代步网格中,以延续前一迭代步中的计算状态,该插值方法可应用于高阶精度自适应流动计算中.为实现流场插值过程中物理量守恒,该方法先计算新旧网格的重叠区域,然后将重叠区域的物理量从旧网格转移到新网格中.为满足高阶精度要求,先采用kexact 最小二乘方法对旧网格上的数值解进行重构,得到满足精度要求的物理量分布多项式,随后采用高斯数值积分实现物理量精确地转移到新网格的各单元上.最后,通过两个算例验证了本文算法的有效性.

本文虽然以二维三角形网格为例阐述高阶插值方法,但其思想同样适应于三维四面体网格情形.不同之处在于,三维情形需要对四面体网格进行求交运算以实现插值过程中物理量守恒,同时插值过程中需要进行体积分计算.下一步的工作,将考虑将本文方法拓展到三维四面体网格的高阶流场插值中.