基于恒等映射多层极限学习机的高速列车踏面磨耗预测模型1)

王美琪 王艺 陈恩利 刘永强 刘鹏飞

(石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

(石家庄铁道大学机械工程学院,石家庄 050043)

引言

自2008 年以来高速铁路在我国迅猛发展,截止到2019 年末,我国高速铁路营业总里程突破3.5 万公里,在线高速动车组3665 标准组,高速铁路运营里程及高速动车组保有量均占世界2/3 以上,稳居世界第一[1].高速列车的发展极大缩短了乘客的出行时间,但是随着车辆运行速度的提高,钢轨的日渐老化,导致了轮轨几何关系的恶化,从而使车轮踏面磨耗愈发严重.这不仅极大增高了高速铁路的运营成本,而且严重影响列车乘坐的舒适性与安全性,列车脱轨等重大事故的发生还会造成国民经济的重大损失[2-3].因此,对车轮磨耗进行趋势预测研究,对高速铁路发展中安全评估与寿命预测有重要的参考意义.

针对上述问题,国内外的专家学者也进行了大量的研究论证.Archard[4]最早提出了接触物体的材料、相对滑动距离影响物体磨耗的磨耗模型.以Archard 磨耗理论为基础,一些国外学者从摩擦学角度[5-6]对车轮踏面磨耗进行了研究,并提出了适用于车轮滚动接触和滑动接触的磨耗机理.文献[7]认为车轮磨耗速率与接触斑面积内能量耗散呈线性关系并以此提出一种车轮磨耗预测模型.文献[8-9]采用结合了轮轨非赫兹滚动接触模型和材料摩擦磨耗模型的车轮磨耗计算模型,并通过车辆多体动力学模型研究了车辆系统参数、轨道系统参数和运营条件对车轮型面磨耗演化规律的影响以及高速列车不同运行里程情况下车轮型面的磨耗分布情况.孙丽霞等[10]采用非线性稳定性及蛇行失稳极限环分析方法,研究了车轮磨耗对车辆蛇行运动稳定性的影响规律.由于轮轨接触融合了车辆动力学、材料学等众多学科,并且轮轨处于一个开放的系统还受到许多不确定因素的影响.上述方法对于轮轨磨耗的研究仅建立在动力学或摩擦学基础上,并且无法使用单一的力学模型对各种复杂工况下的轮轨磨耗进行评估及预测.

近年来随着人工神经网络的发展,基于数据驱动的网络训练与预测在处理非线性问题上具有显著优势[11-17].人工神经网络不仅能够实现多维空间的压缩映射,而且能够实现低维空间的稀疏映射,还能够实现数据的等维映射.姜涵文等[18]通过TensorFlow架构建立了钢轨的通过总重预测模型.程泽华[19]通过BP 神经网络算法构建了接触线磨耗量预测模型.Zhang 等[20]使用LM (Levenberg Marquard)数值优化算法对BP 网络进行优化提出一种自适应差分进化LMBP 轮对尺寸预测模型,对CRH380 BL 型车的轮对尺寸进行了预测.Wang 等[21]通过反向传播神经网络(back propagation neural network,BPNN)对CRH380 BL 的车轮磨耗进行预测及验证.

由此可以看出,人工神经网络凭借其高度的非线性映射能力,被广泛地应用于铁路建设的各个方面,但是随着技术的不断进步,也对网络的性能提出了更高的要求.Huang 等[22]在单隐层前馈神经网络的基础上提出了极限学习机(extreme learning machine,ELM).相对于传统的神经网络,ELM 不仅有较快的学习和训练速度,而且有较高的训练精度,目前已经应用在一些相关领域[23-25].文献[26]结合了PINN (physics informed neural networks)与ELM提出一种PIELM (physics informed extreme learning machine)模型,用于求解复杂几何中的平稳和时变偏微分方程.Kasun 等[27]提出一种使用ELM-AE(extreme learning machine-auto encoder)初始化隐含层权值的分层无监督训练多层极限学习机模型.文献[28]采用外源性输入神经网络建立了轮轨磨损预测的非线性回归模型(nonlinear auto regressive models with eXogenous inputs neural network,NARXNN),用于不同条件下的轮轨磨耗预测.

由此可见,现阶段对于高速列车车轮踏面磨耗预测的研究大多是采用传统的车辆动力学理论,基于数据驱动的高速列车车轮踏面磨耗研究相对较少,在现有的基于神经网络的车轮踏面磨耗预测研究中,选用的网络模型如:多层BP 网络、多层感知器等,均在训练完成后再通过反向传播算法对参数进行微调.这类模型大多泛化能力差,训练速度慢,需进一步开展高速列车车轮踏面磨耗预测的神经网络算法研究.

本文首先在多层极限学习机中引入恒等映射,提出一种基于恒等映射的多层极限学习机模型(IML-ELM),并通过多特征回归数据集验证该模型的网络性能.然后根据高速铁路实际列车参数,建立高速动车组列车的多体动力学模型进行磨耗计算,通过搭建的神经网络模型对车轮踏面磨耗值进行学习和预测,从而验证本文所提出网络模型能较好地反映不同参数对车轮踏面磨耗值的影响规律.最后,利用I-ML-ELM 模型对实际列车的踏面磨耗数据进行学习及预测,进一步验证I-ML-ELM 模型的有效性和适用性.本文采用I-ML-ELM 对高速列车车轮踏面磨耗预测模型进行了研究,以期为高速铁路发展中安全评估提供参考.

1 恒等映射多层极限学习机基本原理(IML-ELM)

1.1 极限学习机

假设有N组训练数据 { (qi,ui)|i=1,2,···,N},L,m和n分别为隐含层、输出层和输入层的神经元个数,g(·) 为隐含层神经元的激活函数,ELM 的数学模型为

式中,H为ELM 隐含层的输出矩阵,U为ELM 的期望输出,β 为ELM 的输出权值.

当输入权值 ωj和隐含层阈值b随机确定后,整个ELM 网络可以看作一个线性系统,网络的训练过程相当于求解方程U=Hβ 的最小二乘解 β,输出权值为

式中,H+为H的Moore-Penrose (M-P)广义逆矩阵.

1.2 极限学习机-自动编码器(ELM-AE)

自动编码器[29]是一种输入、输出神经元个数相等的无监督人工神经网络,主要用于重构输入信号.ELM-AE 是Kasun 等[27]于2013 年提出的一种基于极限学习机改进的自动编码器网络,其网络结构如图1 所示.

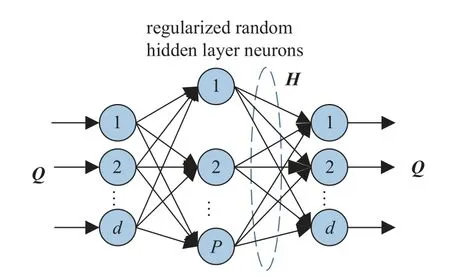
图1 ELM-AE 网络结构图Fig.1 Network structure diagram of ELM-AE

它的主要目的是用三种不同的表示形式有意义地重构输入特征:

(1) 特征压缩,代表特征从高维特征空间映射到低维特征空间;

(2) 特征稀疏,代表特征从低维输入空间映射到高维特征空间;

(3) 特征等维,代表输入空间与特征空间维度相等.

1.3 恒等映射多层极限学习机基本原理(I-ML-ELM)

本文在多层极限学习机基础上对网络结构做出如下改进:在输出神经元与输入神经元之间引入恒等映射,使输出神经元不仅能通过最后一个隐含层的节点获取数据的重新编码,而且可以通过恒等映射从输入神经元直接获取数据信息,增加了网络输出神经元获取数据的丰富性和全面性,从而达到提高网络泛化性与准确性的目的.

恒等映射多层极限学习机的结构如图2 所示,数学模型为

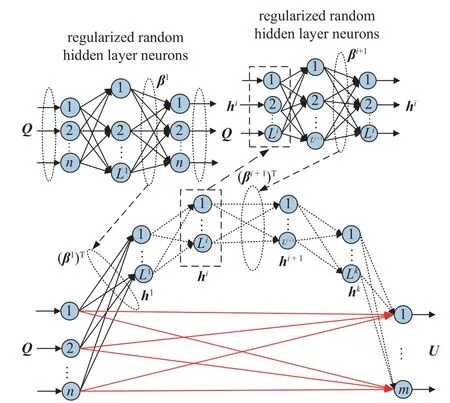
图2 I-ML-ELM 网络结构图Fig.2 Network structure diagram of I-ML-ELM

通过ELM-AE 的训练将I-ML-ELM 隐含层的权值与阈值确定后,整个网络的训练过程可以看作一个线性系统,那么输出权值W就可以通过最小二乘法的形式解析确定,即

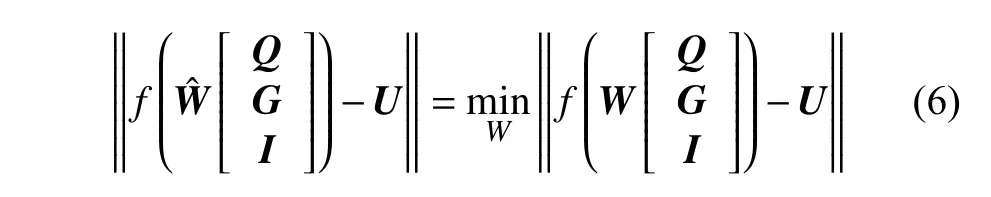
根据Moore-Penrose (M-P)广义逆矩阵算法,式(6)的解为

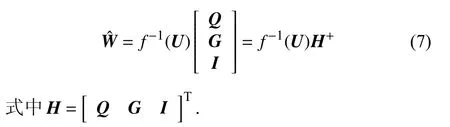
本文建立的恒等映射多层极限学习机模型设定为两个隐含层,学习算法步骤如下:

Step1:随机初始化ELM-AE 的输入权值 ω 和隐含层神经元阈值b;

Step2:使用输入数据对ELM-AE 进行学习与训练得出ELM-AE 的输出权值,存放于I-ML-ELM 的权值栈中;

Step3:将Step2 所得的权重与阈值作为恒等映射多层极限学习机输入层与第一个隐含层的连接权值 β1;

Step4:将I-ML-ELM 第一个隐含层的输出矩阵h1,作为ELM-AE 的训练数据,对ELM-AE 进行训练,获得输出权值,存放于I-ML-ELM 的权值栈;

Step5:将Step4 获得ELM-AE 的输出权值 β2作为I-ML-ELM 第二个隐含层与第一个隐含层之间的连接权值;

Step6:I-ML-ELM 的隐含层权重已经初始化完毕,通过最小二乘法求取I-ML-ELM 的输出权值.

2 实验与分析

恒等映射的引入使得输出层神经元可以直接从输入层神经元获取数据信息,网络的数据来源更丰富,有利于提高模型的泛化性能,以及数据预测的准确性.

为了验证本文提出的预测模型的准确性与泛化性,本文选取machine CPU,wine quality,California housing 和estate valuation 四个多维回归数据集作为样本数据集,上述数据集均来自开源数据库UCI(University of California Irvine) 机器学习数据库,每个数据集70%的数据用作训练数据,其余作为测试数据,四个数据集的基本信息如表1 所示.

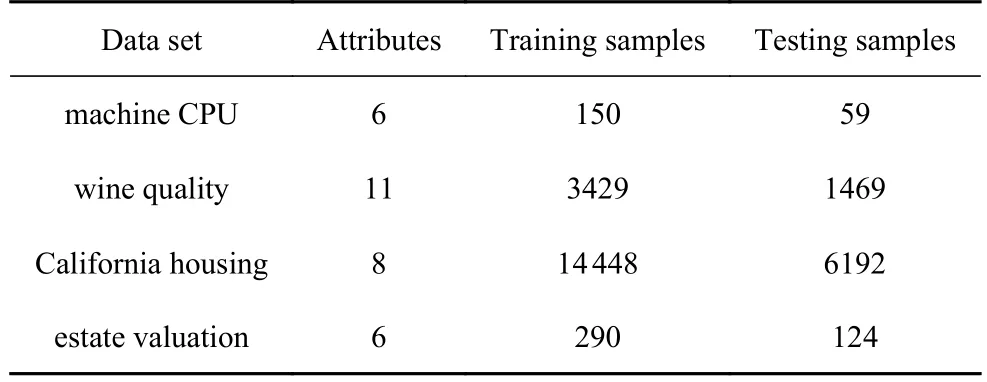
表1 数据集的基本数据信息Table 1 Basic data information of data set

本文选取五种网络:ELM,FLN,DLSFLN,MLELM,ML-KELM,与本文提出的I-ML-ELM 网络模型进行对比.其中ELM,FLN,DLSFLN,ML-ELM 中的激活函数均为Sigmoid 函数,ML-KELM 网络中的内核函数类型为RBF 型.ML-ELM,ML-KELM 网络的隐含层数量与I-ML-ELM 一致.

本文对两隐含层神经元个数进行单一变量分析,采用控制变量法对两隐含层神经元个数进行分析,其结果经可视化处理后如图3 所示.将网络输出的均方根误差值RMSE 作为网络精度的表征值,RMSE 值的计算如式(8)所示,数据经可视化处理,可视化处理如式(9)所示

式中,为原始数据的均值,uσ为原始数据的标准差.

在N1ON2平 面以上为数值大于数据均值,在N1ON2平面以下为小于数据均值.RMSE值越小表明网络的精度越高,本文以1 为步长,两层神经元个数由1 增加到30,N1,N2分别为第一个隐含层、第二个隐含层神经元个数.由图3 可以看出,第一个隐含层神经元个数不变时,随着第二个隐含层神经元个数增多,网络的精度逐渐提高,但是随着神经元个数的持续增长,网络精度不再提高.第二个隐含层神经元个数不变时,随着第一个隐含层神经元个数的增多,网络的精度出现一定程度的波动后不再变化.所以本文选定第一个隐含层神经元个数为1,第二个隐含层神经元个数为7.

图3 不同隐层神经元条件下的网络回归精度变化趋势Fig.3 Variation trend of network regression accuracy under different hidden layer neurons

为了进一步分析模型预测效果及准确度,选取以下四种经典的网络性能评价指标作为预测效果评判标准:均方根误差RMSE、最大绝对误差MAXE、平均绝对误差MAE、平均绝对百分误差MAPE.上述四种值越小表示测试输出越接近测试数据的期望输出.指标的计算公式如式(8)、式(10)～式(12)所示

RMSE值代表模型的回归精度,数值越小,说明该方法的预测准确度越高.由表2 可以看出,I-MLELM 算法在不同数据集下的RMSE值分别为0.0322,0.0015,0.1399,0.0012,小于其他五种算法在同一数据集下的RMSE值.在estate valuation 数据集下ELM,FLN 的RMSE略小于I-ML-ELM 算法的RMSE值,但是ELM,FLN 在其他数据集下的RMSE值,并没有表现出比I-ML-ELM 算法更好的效果.所以从总体的RMSE值来看,本文提出的I-ML-ELM 算法在表中所示的网络中回归精度更高并且在四种数据集下的综合效果最好,在不同数据集下的适用性也更高.

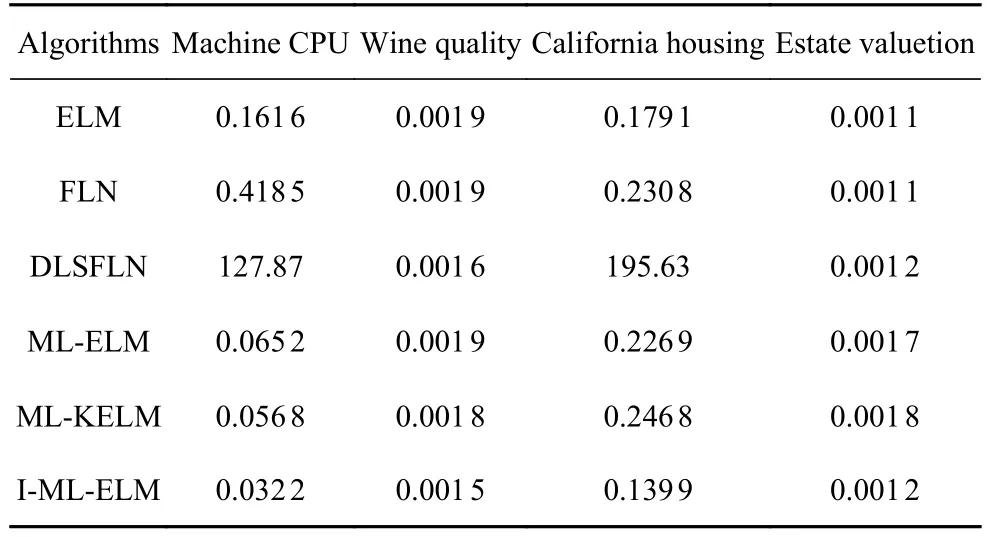
表2 算法在不同网络下数据集RMSE 值比较Table 2 Obtained RMSE by different networks of the algorithm

MAXE,MAE和MAPE多用于反映预测误差的实际情况.

如表3 所示,I-ML-ELM 算法在不同数据集下的MAXE值分别为0.1284,0.0072,1.2638,0.0048,该值小于其他几种算法在同种数据集下的MAXE值.

由表3 可以看出ML-KELM 在某一数据集中的MAXE值略小于I-ML-ELM 的MAXE值,但是ML-KELM 在其他数据集,以及表4 表5 所示的评价指标中性能表现并不优越.所以整体来看I-ML-ELM 算法在四种数据集下的预测误差依然优于其他算法.

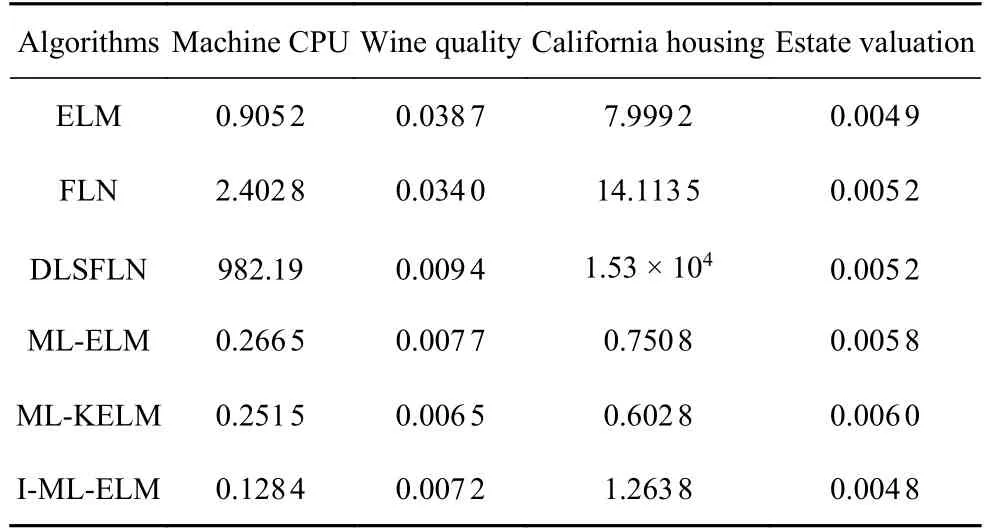
表3 算法在不同网络下数据集MAXE 值比较Table 3 Obtained MAXE by different networks of the algorithm

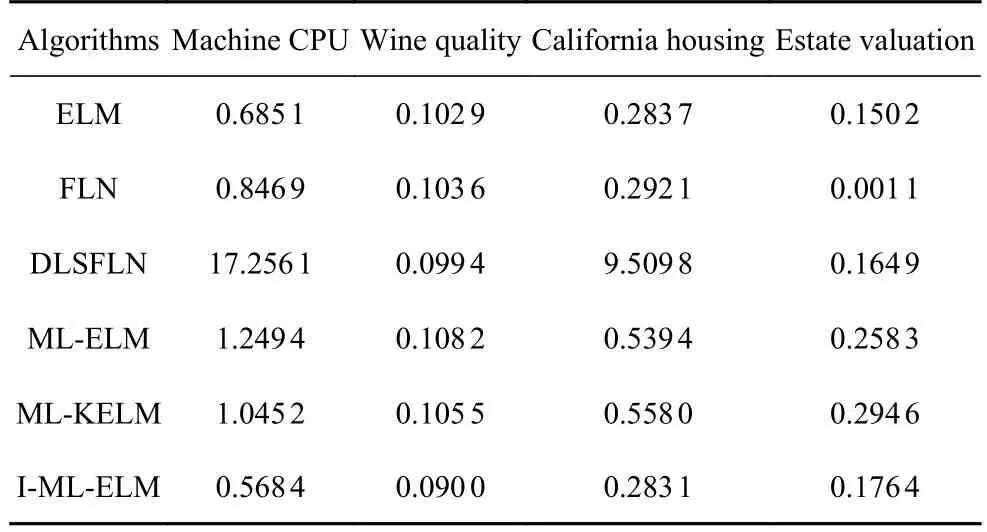
表4 算法在不同网络下数据集MAPE 值比较Table 4 Obtained MAPE by different networks of the algorithm

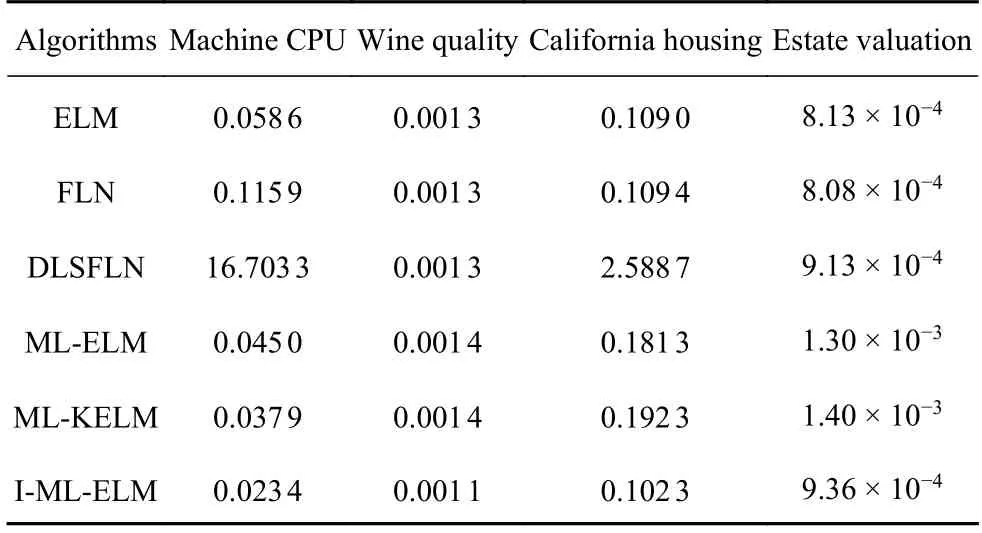
表5 算法在不同网络下数据集MAE 值比较Table 5 Obtained MAE by different networks of the algorithm

纵观RMSE,MAXE,MAE,MAPE四种性能指标,本文所提出的I-ML-ELM 算法在各项指标中的综合性能优于其余五种算法,网络的回归精度更高,泛化性能更好.

表6 给出了几种不同算法在同一数据集下的网络预测耗时对比,本实验均在处理器AMD R52600、主频3.4 GHz、内存16 GB、Windows1064 位操作系统、软件Matlab 2020a 环境下进行,由于在网络训练过程中隐含层权值与阈值为随机给定,故表6 中数据均由网络运行30 次,取30 次测试时间的平均值进行对比.

由表2 至表5 的对比结果,可以看出本文提出的I-ML-ELM 网络具有较高的准确性和较好的泛化性能,结合表6 可以看出,该网络同时也具备了较高的计算效率.在estate valuation 数据集下的表现略差于ML-KELM,但综合四种数据集及其他几种性能指标来,看I-ML-ELM 算法的网络综合性能依然优于其他算法.

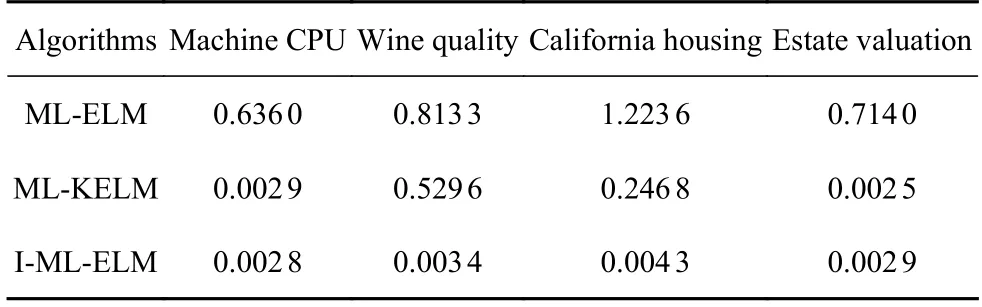
表6 算法在不同网络下数据集的测试时间(s)比较Table 6 Data test time (s) comparison of the algorithm under different networks

3 车轮磨耗预测实验分析

3.1 车辆-轨道耦合动力学模型建立

根据车辆-轨道耦合动力学理论及高速列车的实际参数,如表7 所示,建立了单节车厢的车辆-轨道耦合动力学模型.

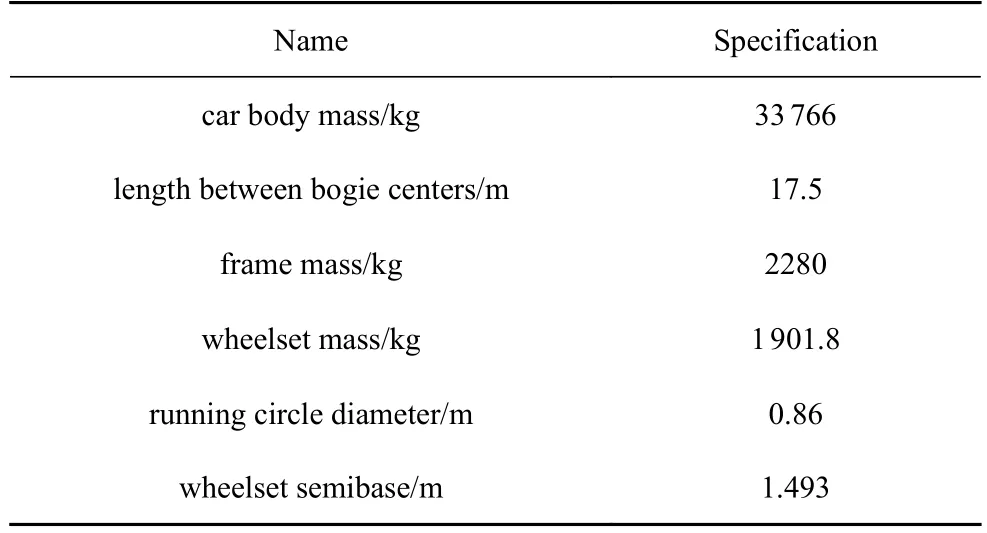
表7 高速列车主要参数Table 7 Basic parameters of high-speed vehicle

车体模型主要由1 个车体、2 个构架、4 个轮对等部件组成,其中车体、构架、轮对均包含横向、垂向、纵向、侧滚、点头、摇头6 个自由度,轴箱为1 个自由度,整车共计50 个自由度.

车体和转向架之间通过二系悬挂进行连接,二系悬挂包括空气弹簧、二系横向减振器及抗蛇行减振器.转向架和轮对之间通过一系悬挂进行组合,一系悬挂装置包括一系垂向减振器、转臂轴箱和一系钢弹簧.

轨道采用移动质量轨道模型,在定义了轨道垂向和横向的总体刚度和阻尼后,增加了钢轨模型.并且轨道始终跟随车轮,具有等效质量和转动惯量,钢轨地面之间采用弹簧阻尼相连.

3.2 车轮踏面磨耗模型

Archard 模型[4]中磨耗体积与法向力、滑动距离成正比,与材料硬度成反比,即

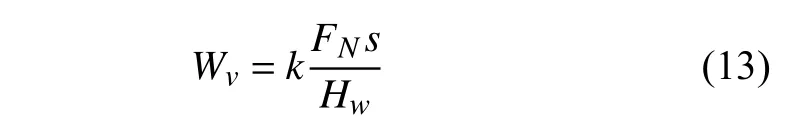
其中,Wv是磨耗体积,FN是法向力,s是滑动距离,Hw为材料硬度.k是无量纲磨耗系数,取值与接触应力和滑动速度有关,其关系如图4 所示(该磨耗图[30]根据摩擦实验建立).

图4 磨耗系数分布图Fig.4 Wear coefficient map

本文采用UM 中基于摩擦功的Archard 磨耗模型,该模型认为磨耗体积与摩擦功呈线性关系为

其中,P是摩擦功率,即

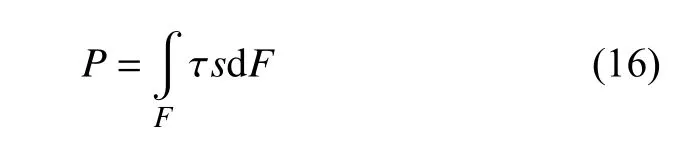
式中,τ 是接触单元内的切向应力,s是滑动速度,F是接触斑面积.

3.3 轮轨滚动接触力学模型

当高速列车运行在复杂工况时,轮轨的接触关系不符合Hertz 接触理论,故本文采用基于虚拟渗透法的轮轨非椭圆多点接触算法(K-P 算法)[31]计算轮轨法向力.

对于轮轨接触的法向接触应力pz(x,y) 计算方式为

式 中,δ0为 渗透 量;k(y)=zwheel(y)−zrail(y) 代 表x=0平面上车轮型面曲线zwheel(y) 与钢轨型面曲线zrail(y)两点间的距离.

轮轨接触斑面积近似服从下式

由此可通过积分运算得到轮轨接触法向力

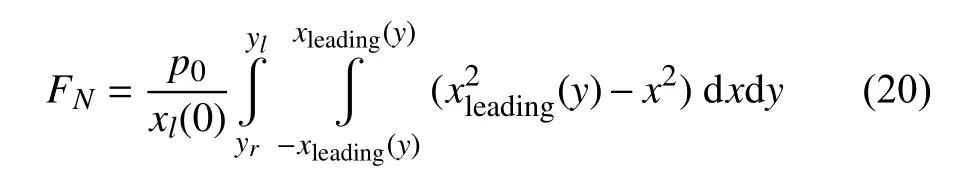
式中,yl表示在y方向的接触斑边界.

点(0,0)处的法向变形位移为

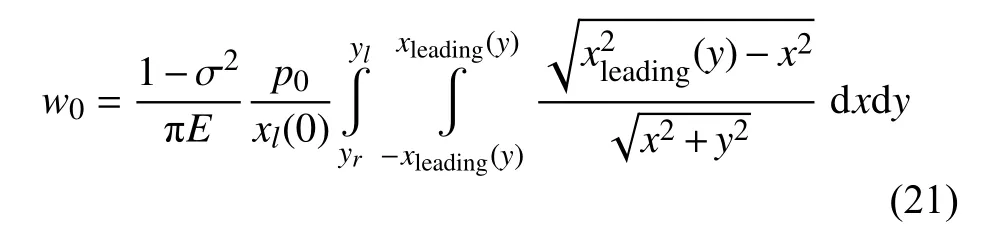
式中,σ 为泊松比,E为杨氏模量.(0,0)处的渗透值为 δ0=2w0(0,0)=2w0,可得轮轨接触法向力

采用针对非椭圆接触面修正的FASTSIM 算法计算切向力.将接触斑等效成椭圆接触斑,需满足以下两个条件:

(1) 等效椭圆的长短轴之比与K-P 模型得到的接触斑长宽之比相等;

(2) 等效椭圆的面积与K-P 模型计算得到的接触斑面积相等.

那么接触区域中切向应力的分布为

式中,vx,vy和 φ 分别为纵向、横向和自旋蠕滑率,在接触斑内对式(23)和式(24)进行积分即可求得接触力.

3.4 仿真分析

在车轮磨耗仿真中,假设车轮踏面形状在更新前始终保持不变,每次迭代计算以车辆运行里程值作为车轮踏面更新的判断依据.迭代次数为磨耗模拟的重复次数.磨耗迭代是对相同结构的一系列计算,只是在初始踏面廓形上有所不同,一次迭代是对一组配置的单个计算.里程是分配给一个磨耗步骤的里程,在每一个磨耗步骤结束时,里程值用来衡量磨耗深度.磨耗步数为一次迭代中踏面廓形更新的次数,步数越多且里程越少,则踏面廓形演进越接近实际,但是建模时间也越长.因此本实验中磨耗步数设为2000,里程设为5 km.

基于建立的高速列车车辆-轨道耦合动力学模型,通过多体动力学软件采用控制变量法对不同运行速度、运行里程及不同曲线半径的线路进行磨耗仿真计算,得到相应的踏面磨耗值,并对数据进行对比分析.最后通过恒等映射多层极限学习机数据预测模型,对踏面的磨耗深度进行学习和预测.

图5 为列车在曲线半径为8000 m 的线路中以300 km/h 速度运行,获取到不同运行里程下转向架左前轮的车轮磨耗变化趋势及磨耗深度.通过图5可以看出,车辆运行10000 km 时踏面磨耗深度约为0.12 mm.随着运行里程的增加,车辆运行到50000 km时,车轮踏面的磨耗范围变大,踏面磨耗深度在0.5 mm 左右.当运行到155000 km 时,踏面磨耗深度在1.4 mm 左右.主要的磨耗区间为(−30 mm～30 mm),轮缘部分基本没有磨耗,车轮磨耗量最大值是0.9 mm 左右,磨耗最深处位于车轮踏面10 mm 附近.由此我们可以看出,车轮踏面磨耗主要位于车轮名义滚动圆附近,并且向两侧延伸.

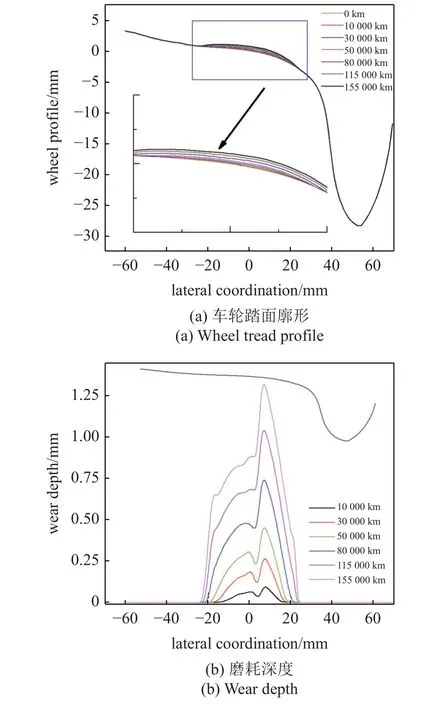
图5 列车运行不同里程时踏面廓形及磨耗深度Fig.5 The tread profile and wear depth under different mileage of train operation

改变列车的运行速度时,车轮的踏面磨耗值也会发生相应的变化,图6 为列车在不同运行速度下运行100000 km 时的踏面的磨耗深度及最大磨耗深度.

由图6(a)可以看出,随着车速的提高,车轮踏面的最大磨耗深度随着运行速度的升高呈现升高的趋势,并且升高量越来越大.列车的运行速度在300 km/h 时,车轮踏面最大磨耗深度为0.9 mm;当列车运行速度达到350 km/h 时,车轮最大磨耗深度为0.923 mm;当列车运行速度达到380 km/h 时,车轮踏面的最大磨耗深度到达了0.98 mm.由图6(b)可以看出,列车在不同运行速度下,对磨耗的主要区域也有影响.当车辆运行速度为250 km/h 时,踏面磨耗深度约0.88 mm,随着车辆运行速度的提高,主要磨耗区间出现微小延展但基本没有变化,但是当速度达到380 km/h 时,磨耗区域有明显延展,向左侧延伸约1 mm,向右侧延伸约5 mm.

图6 不同车速下列车运行100000 km 磨耗深度Fig.6 100000 km wear depth of train running at different speeds

对于线路条件的设定本文采用单一线路条件的设定,其中曲线部分曲线半径的取值通过机车车辆动力学性能评定及试验鉴定规范选择.由仿真结果可以看出,当列车通过不同曲线半径的线路时,对车轮踏面磨耗的影响也是不同的.

由图7 可以看出,车轮踏面的最大磨耗值随着曲线半径的增大呈现出先减小后平稳的趋势.7000 m 的曲线半径值作为转折点,当列车通过线路的曲线半径小于7000 m 时,随着曲线半径的增大,踏面的最大磨耗值呈现大幅减小,当列车通过线路的曲线半径大于7000 m 时,踏面的最大磨耗深度值趋于平稳.

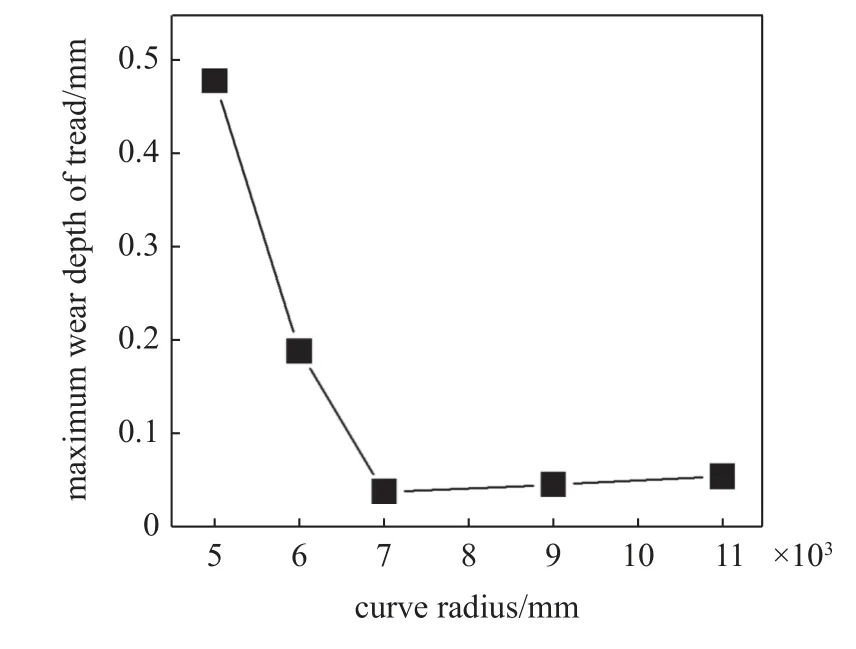
图7 不同曲线半径下车轮磨耗深度值Fig.7 Wheel wear depth under different curve radius

通过以上的数据分析及对比,可以看出,在不同的速度、运行里程和曲线半径的情况下,车轮的踏面磨耗会有相应的变化.因此本文选择行车速度、运行里程和线路曲线半径作为神经网络的输入变量.通过在UM 中获取到的315 组数据作为数据集,其中221 组作为训练数据集,剩余94 组作为测试数据集,使用不同的算法对车轮的磨耗深度值进行预测.其结果如表8 所示.

由表8 可以看出,本文所提出的I-ML-ELM 模型的RMSE,MAXE,MAPE,MAE值远小于其他算法,也就是说I-ML-ELM 预测模型,在车轮踏面磨耗预测方面表现出比其他五种算法更好的网络性能.由此可以看出,I-ML-ELM 模型能准确地建立列车不同的运行参数与车轮磨耗之间的映射关系,通过改变列车的运行参数,可以得到不同的踏面磨耗值,可有效用于车轮踏面磨耗的预测.

表8 不同网络模型在仿真数据下的性能参数Table 8 Performance parameters of different network models under simulation data

3.5 实测数据分析

通过铁路现场对该型高速列车一节车厢进行跟踪和测量获取的车轮踏面数据如图8 所示.由图像可以看出,踏面的主要磨耗区域为(−20 mm～20 mm),随着列车运行里程的增大,磨耗程度不断加深,其中镟后车轮到运行80000 km 时磨耗增长速率较快,运行80000 km 到115000 km 时增长较平缓.镟修后的车轮,运行到115000 km 其磨耗增长约0.45 mm.

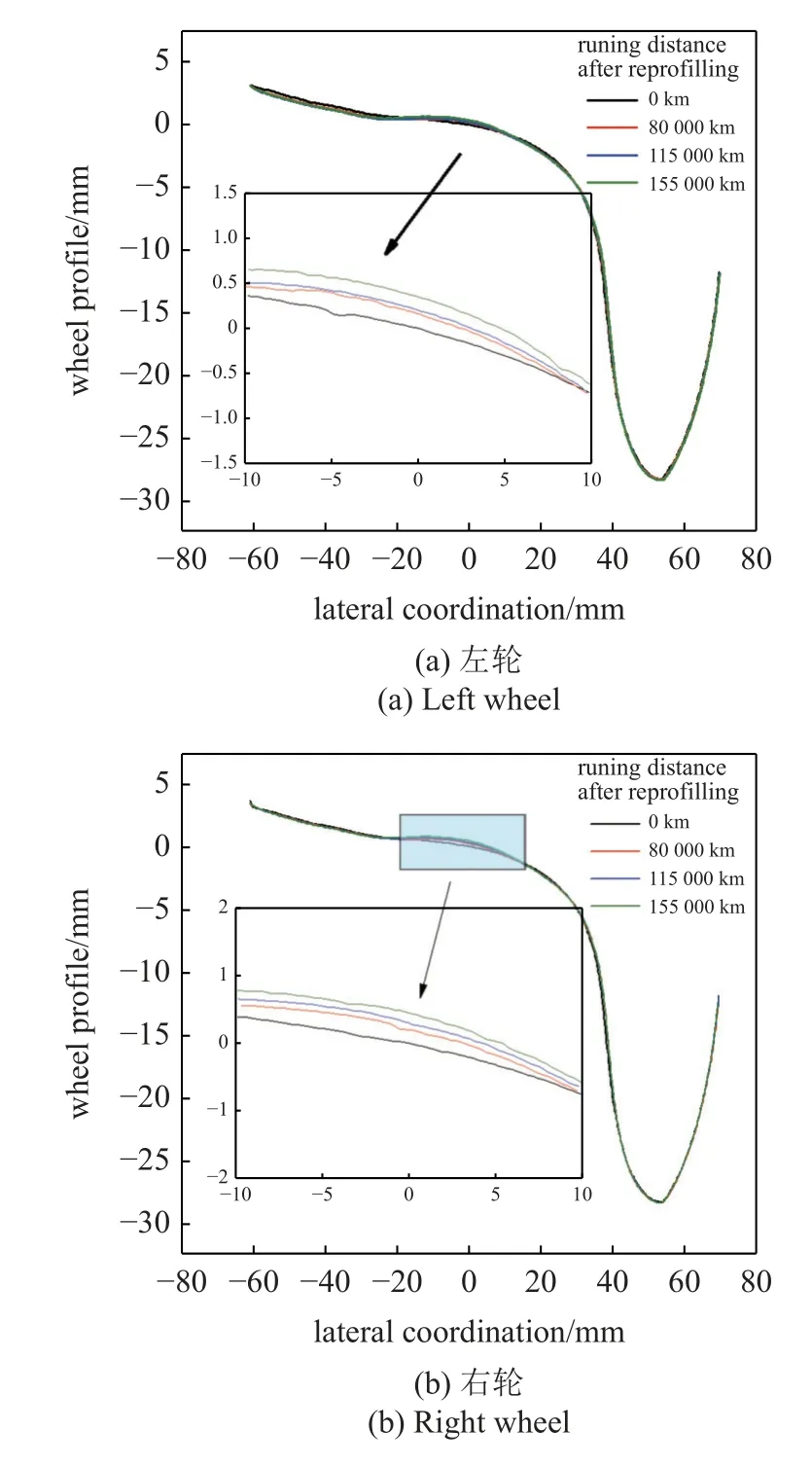
图8 实测列车运行不同里程下车轮踏面廓形图Fig.8 Measured wheel tread profile under different mileage of train operation

为了进一步验证I-ML-ELM 模型的预测精度和有效性,将列车运行里程作为输入变量,车轮踏面名义滚动圆处的磨耗深度作为输出,使用本文提出的I-ML-ELM 预测模型进行训练及预测,结果如图9及表9 所示.通过对比实际测量值和神经网络预测值,从而验证I-ML-ELM 模型预测的准确性.通过表9 可以看出,本文所提出的I-ML-ELM 神经网络模型的RMSE,MAXE,MAPE,MAE值均小于其他网络,说明本文提出的预测模型在踏面磨耗预测方面优于其他网络模型.

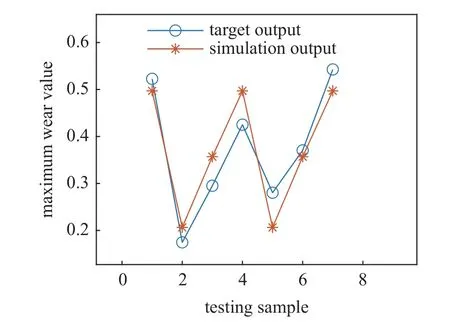
图9 测试样本的踏面磨耗预测值和实际测量值对比图Fig.9 Comparison between predicted value and sample value of testing sample of wheel tread wear value

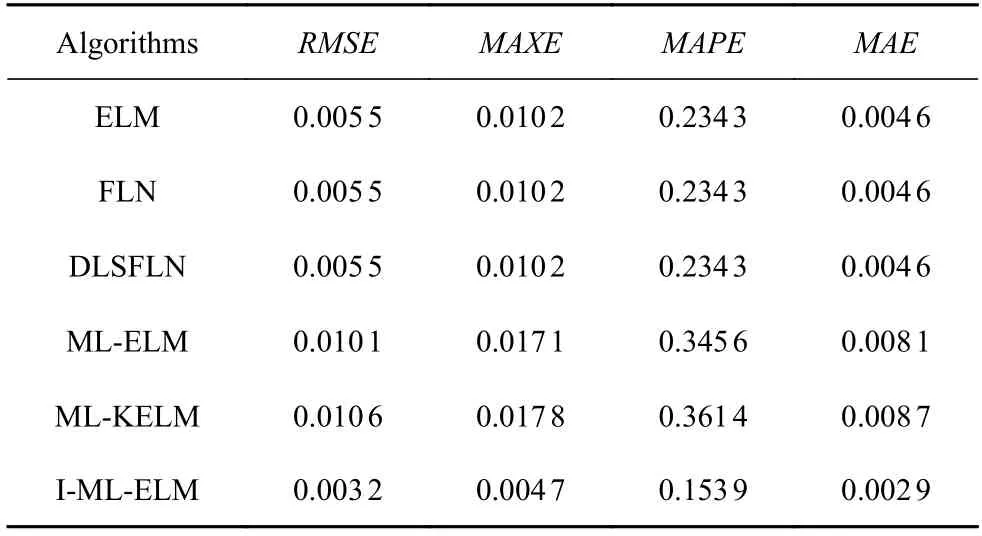
表9 不同模型在现场数据下的性能参数Table 9 Performance parameters of different algorithms under field data

4 结论

在多层极限学习机中引入恒等映射,提出一种恒等映射多层极限学习机模型,建立了基于恒等映射多层极限学习机的高速列车车轮踏面磨耗预测模型.通过I-ML-ELM 磨耗预测模型对高速列车车轮踏面磨耗量进行了学习及预测,以期为车轮的安全评估提供参考.本文的主要结论如下.

(1) 提出恒等映射多层极限学习机算法,并通过不同类型、不同数据量的公共数据集进行了性能测试,验证了I-ML-ELM 模型具有较高的预测精度与较好的泛化性.

(2) 提出了一种基于恒等映射多层极限学习机模型的车轮踏面磨耗预测方法,通过I-ML-ELM 模型对不同工况条件下的磨耗值进行学习和预测,验证了该模型的有效性.

(3) 对不同工况下高速列车模型最大磨耗深度值的预测结果表明,本文所搭建的恒等映射多层极限学习机模型的性能参数指标均优于ELM,FLN,DLFLN,ML-ELM 和ML-KELM.仿真结果表明相对于其他神经网络模型,本文中所提出的I-MLELM 预测模型对高速列车踏面磨耗深度值的预测值更接近实际测量值,从而验证了I-ML-ELM 具有较高的预测精度.