爬壁机器人系统的广义Lagrange方程

陆晓丹，张港

（1.浙江理工大学理学院，杭州 310018；2.浙江同济科技职业学院，杭州 311231）

0 引言

爬壁机器人可以协助人们在复杂危险的环境中进行工作，应用领域十分广泛，因此在材料学、力学、物理学、数学、生物学、现代科学和工程技术领域等受到广泛关注。研制爬壁机器人有两个最需要考虑的因素：一个是爬壁机器人的移动方式；另一个是爬壁机器人的吸附方式[1]。从爬壁机器人的吸附方式上来说，主要可以分为真空吸附、磁吸附、仿生吸附、背推式吸附[2-5]。本文主要从运动机能上研究爬壁机器人。根据移动方式的不同，爬壁机器人主要分为轮式、履带式和足式[6]。各种移动方式的对比如表1所示。

表1 不同移动方式对比

未来爬壁机器人的研制将朝着灵活性高、体型小、操作智能化等方向发展。目前，轮式和履带式爬壁机器人已经得到广泛应用，而四足式仿壁虎型爬壁机器人具有得天独厚的优势，从而在实际的应用中能得到更为广阔的发展[7]，因此本文以美国斯坦福大学研制的四足式仿壁虎型StickyBot III爬壁机器人[8]（如图1）为研究对象。

图1 StickyBotIII爬壁机器人

爬壁机器人系统动力学模型的建立，有助于分析爬壁机器人的性能，设计控制算法及评估机器人移动位置所需要的关节力矩等，可以为未来爬壁机器人的动态优化、控制算法、智能化和路径规划等提供强有力的理论支撑[9]。建立动力学方程的方法有很多种，许多国内外学者对不同类型的爬壁机器人采用多样的方法进行动力学分析并得到相应的动力学方程，在此做一些简单介绍。Xu等[10]利用牛顿力学的方法建立了轮式爬壁机器人系统的动力学方程，分别对系统处于光滑面和越障两种不同状态进行受力分析，建立了越障过程中系统的车轮和机身动力学方程；岳荣刚等[11]以City-Climber履带式爬壁机器人为原型，利用牛顿力学的方法，建立了该机器人在地面、垂直墙壁和天花板不同环境下的动力学方程，该方程的建立为City-Climber机器人的路径规划和避障问题提供了良好的解决方案，但上述两个建模过程都较为复杂。徐亚茹等[12-13]利用U-K方程建立了轮式爬壁机器人的解析动力学方程。事实上，利用U-K方程进行建模需先利用Lagrange力学法建立系统在未受约束情况下的动力学方程[14]，进而利用U-K方程建立该系统的动力学方程；并且徐在建模过程中并未考虑轮子与壁面之间摩擦力和轮子的转动惯量，但在实际情况中，这两个是必须考虑的因素，因此本文将该因素考虑其中，以增强模型的适应性。此外还有学者利用D-H法、牛顿-欧拉法等[15-18]建立了爬壁机器人系统的动力学方程。

以上几个典例是构建爬壁机器人系统动力学方程的几种常见的方法，但可以看到，其过程都较为复杂，且爬壁机器人系统是一个复杂的多体约束力学系统，利用牛顿力学法对其受力分析时也较容易出错。本文利用Lagrange力学分析法，将爬壁机器人看作一个系统，选用广义坐标，计算该系统的动能和势能，定义系统的Lagrange函数，写出系统的非完整约束方程，并计算系统受到的外力和耗散函数，最后给出爬壁机器人系统的广义Lagrange方程。

1 爬壁机器人的动力学分析

1.1 爬壁机器人四肢动力学分析

首先计算爬壁机器人系统四肢相对于身体的坐标和速度。

根据爬壁机器人的肢体形态特点，考虑爬壁机器人的运动形态，为简化起见，将爬壁机器人系统四肢各关节看成是1个自由度的转动关节，并将爬壁机器人的单支腿简化为如图2所示，简化结构由身体0、股骨1、胫骨2和脚掌3组成。

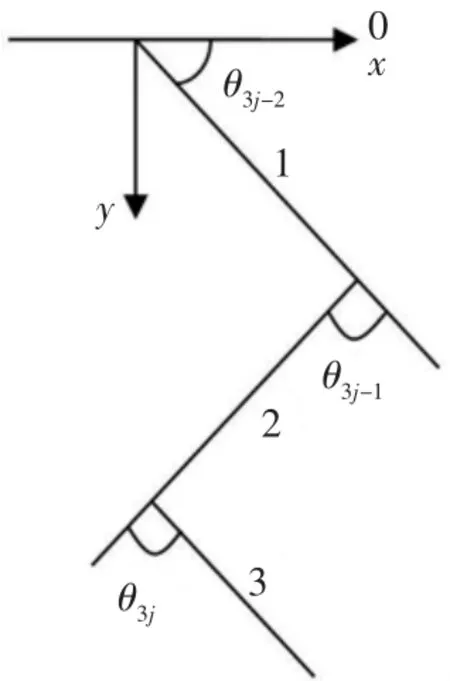
图2 单肢结构简图

其中构件1和构件0的连接处为髋关节，构件1和构件2的连接处为膝关节，构件2和构件3的连接处为踝关节。定义θ3j-1、θ3j-2、θ3j等四肢各关节的倾斜角度（其中j为爬壁机器人四肢的数量）。为方便起见，假设爬壁机器人系统四肢各关节长度相等为l，质量相等为m′，同时引入qi=θi（i=1，2，…，15）作为广义坐标，并用广义坐标表示直角坐标。

那么，爬壁机器人的股骨相对于身体的质心坐标可用广义坐标表示为：

胫骨相对于身体的质心坐标可用广义坐标表示为：

1.2 爬壁机器人机身动力学分析

接下来研究运动过程中爬壁机器人机身中心位置坐标及速度变化。

爬壁机器人的工作环境一般为竖直的平面、圆柱面和圆锥面等，本文基于圆锥壁面的工作环境下讨论，因为圆锥壁面较其他壁面复杂，所以只要解决了爬壁机器人在圆锥壁面上的运动学原理，那么在其余工作环境下的运动学问题也就迎刃而解。现将爬壁机器人的工作壁面的图形简要画出（如图3）。

图3 爬壁机器人工作壁面简图

在地面中心创建一个固定的笛卡尔坐标系{x，y，z}，则在圆锥壁面工作环境下，爬壁机器人的质心位置根据几何学可用下面的公式表示：

1.3 爬壁机器人系统动力学分析

设爬壁机器人在攀爬过程中不发生侧滑，只存在静摩擦，可以得到非完整约束条件为

2 爬壁机器人系统的运动微分方程

2.1 爬壁机器人系统的Routh方程

采用Lagrange乘子法，得到非完整爬壁机器人系统的运动微分方程，即Routh方程为：

式中：Qi=Qi（t，q，q˙）为非完整爬壁机器人系统的非势广义力；F为爬壁机器人4条腿各关节之间的摩擦耗散函数，假设爬壁机器人系统脚掌与地面之间的平动和转动的摩擦因数分别为μ1和μ2，因此爬壁机器人系统的摩擦耗散函数为

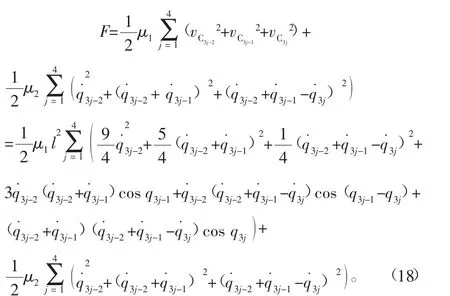
其中，vc3j-2、vc3j-1、vc3j分别为爬壁机器人系统中四肢各关节中心位置的速度。

2.2 爬壁机器人系统的Lagrange方程

设系统（16）非奇异，即det（∂2L/∂q˙s∂q˙k）≠0（s，k=1，2，…，15），则由式（10）和式（16）可求出所有λj=λj（t，q，q˙），（j=1，2，3，4），式（16）便可写为

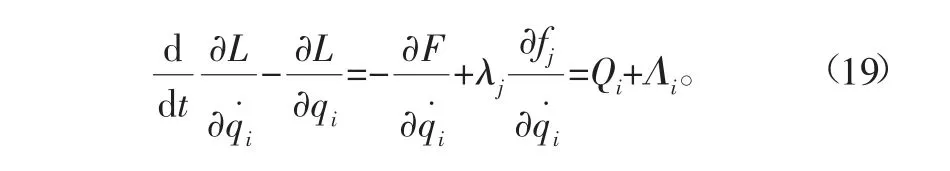
式中：

式中，Λi为广义约束反力。

式（19）为非完整爬壁机器人系统方程式（10）和式（16）相应的完整系统的运动微分方程，即Lagrange方程。

3 爬壁机器人系统的广义Lagrange算例

通过以上讨论，已经得出非完整爬壁机器人系统在圆锥壁面上的Lagrange函数及非完整爬壁机器人系统Routh方程式（16）和相应完整系统的Lagrange方程式（19）。现给出圆锥壁面上具体的广义Lagrange方程。将式（10）、式（15）、式（18）代入式（16）得：

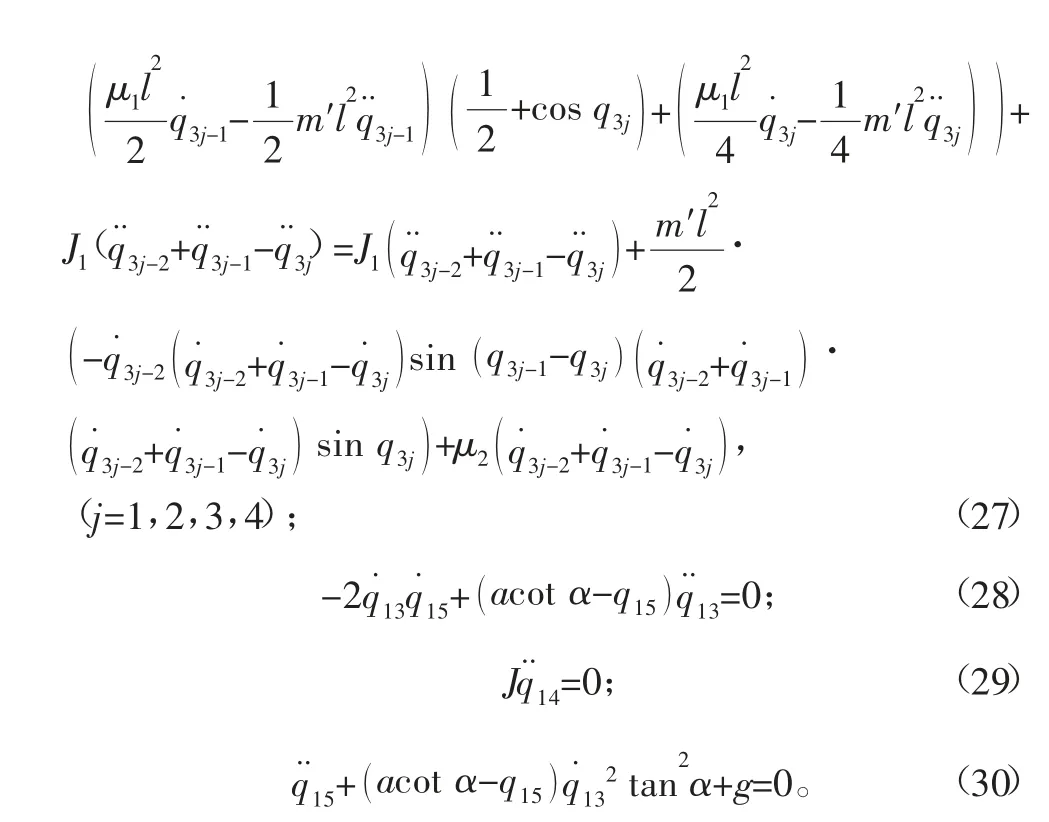
4 结论

本文将Lagrange力学法引入到四足式爬壁机器人系统，根据爬壁机器人系统运动过程分析了爬壁机器人系统的动能、势能及所受的非完整约束，给出爬壁机器人系统的Lagrange函数并建立了该系统广义Lagrange方程。在最后给出爬壁机器人系统广义Lagrange算例，求出在圆锥壁面上非完整爬壁机器人的Lagrange乘子（24），得到非完整爬壁机器人系统相应完整爬壁机器人系统的运动微分方程即Lagrange方程。利用Lagrange力学方法研究四足式爬壁机器人系统更为简便，形式上也具有较高的统一性。

在本文取得成果的基础上，可以引入Lie群分析法，建立该系统的对称性理论，得到相应守恒量，从而得出爬壁机器人系统的运动规律。