“数回”冬日
2022-07-10阮征
阮征





啦啦啦,啦啦啦,我是播报的小行家,一边走一边报。今天的热点真正好,快来组队看报道。
炎炎夏日,只有手里的冰棍能带来一丝凉意。看着家中的“过气明星”冰墩墩,你是否还记得今年2月的那场盛宴——北京冬奥会呢?
今天,就让我们用数学带大家一起“数回”冬日,为大家解解暑吧!
雪花的秘密
雪花是冬天不得不提的一位客人。雪花是空气中的水汽遇冷后凝华而来的固态晶体,结构随温度的变化而变化。在飘落过程中,雪花们逐渐聚集成团,就形成了雪片。
在平面上,正六边形的排列方式是最致密的,也是最有效率的布置方式。大自然中的许多物体都含有六边形结构,雪花也不例外。雪花的结晶体都是有规律的六角形,将其各角连起来,就变成一个近乎完美的六边形。所以,古人又有“草木之花多五出,独雪花六出”的说法。
也许大家曾听过:世上没有两片完全相同的雪花。这又是为什么呢?关于这个问题,有着无限周长的雪花曲线或许能解答你的疑问!
雪花曲线
雪花曲线是由瑞典数学家科赫发现的,所以又称为科赫雪花,是一种分形曲线。
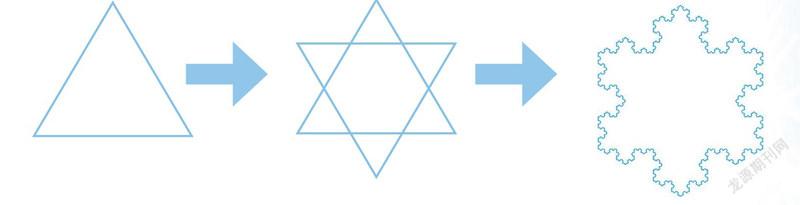
1904年,瑞典数学家科赫提出了一种图形画法:将一个正三角形的每条边平分成三份,再以每条边中间的一份为边,向外作正三角形,这个过程称为第一次迭代。
经过第一次迭代,正三角形变成了有着十二条边的“星”形。接着,再将每个正三角形的每条边平分成三份,向外作更小的正三角形,这样的过程称为第二次迭代……不停地重复这个过程,经过无限次迭代后,科赫雪花就诞生了!
科赫雪花有很多特点。我们可以把科赫雪花不断地放大,然后通过观察发现,无论是多小的一段,雪花都依然保持了和原来一模一样的崎岖结构,这种性质称为“自相似性”。
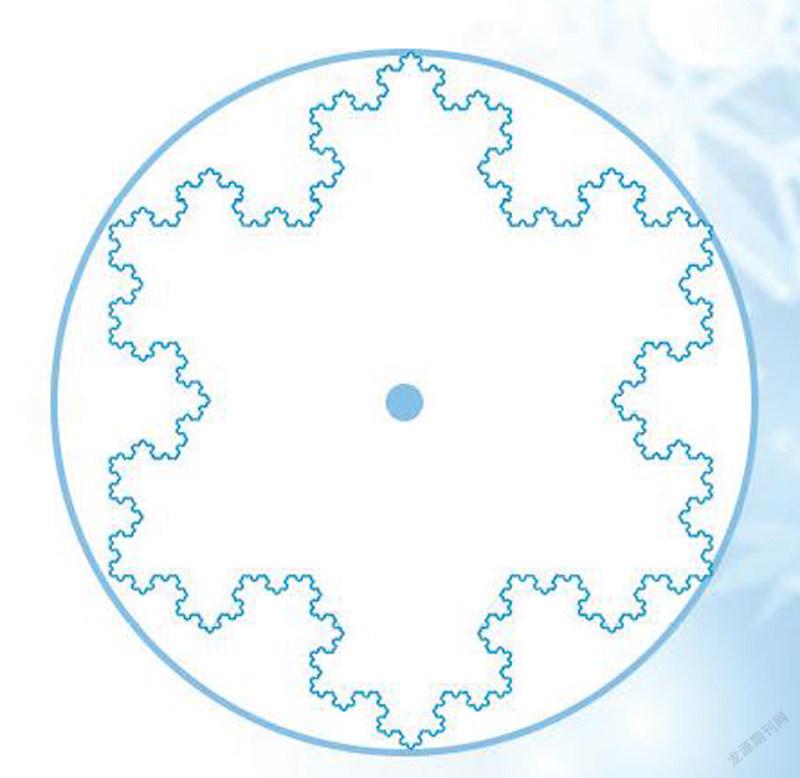
我们还可以将初始正三角形的各个顶点用曲线连接起来,这样便可画出一个外接圆。但不论经过多少次迭代,图形都始终位于圆内。这证明科赫雪花的面积小于外接圆的面积,也就是说它的面积是有限的。但面积有限的科赫雪花,其周长却是无限的!
科赫雪花每次迭代时都会有数段直线“凸”起,形成多个新的角。根据“两点之间直线最短”可以判定,图形每次迭代时,其周长都是在增加的。正如前文所说,科赫雪花是经过无限次迭代后得到的,其周长增加了无限次,那周长自然也是无限的。
实际上,雪花的形状还受自然因素的影响,远比科赫雪花复杂。有如此多造型可“凹”的雪花,自然是一人一件“新衣服”,都不会“撞衫”啦!
冬奥会上,火炬最终就在一朵巨大的雪花里闪烁升腾,而这朵巨大又复杂的雪花则是通过科赫雪花迭代而成的。除了雪花外,当其他冬奥元素与数学相碰撞时,又会擦出怎样的精彩火花呢?
奖牌与引导牌
如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形,这条直线叫对称轴。圆是典型的轴对称图形,直径就是圆的对称轴,所以圆有无数条对称轴。冬奥会的奖牌是圆的,奖牌中央的奥运五环是由五个圆组成的轴对称图形。
而将一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么这两个图形关于这个点成中心对称。雪花引导牌就是中心对称图形。
滑雪与眼镜
当运动员在冬奥会的滑雪比赛场上滑行的时候,我们能够看到一条优美的曲线轨迹。关于这条曲线,它还有个优美的名字——抛物线!
在数学中,抛物线是一条镜像对称的平面曲线,并且形状大致为U形或倒U形。抛物线具有许多重要的应用,如天线、麦克风、计算导弹弹道等。
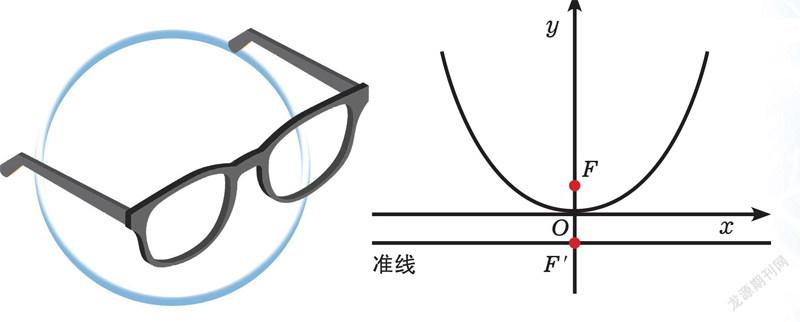
我們日常使用的近视眼镜就和抛物线有关。抛物线的对称轴上有一个焦点F,过点F关于x轴的对称点F′、且与抛物线对称轴垂直的直线被称为准线。抛物线上的点到点F和准线的距离相等。医生将抛物线看作近视眼镜,准线看作我们的眼睛,根据我们的视力确定焦点,很快就能为我们推荐合适的近视眼镜。
正负数
北京冬奥会由北京和张家口主办。为什么选张家口而不是温度更低的东北?除了距离原因,温度也有很大关系。历届冬奥会均在2月份举办,-17℃~10℃则是最理想的温度。这里的-17就是一个负数!
若一个数大于零,则称它是一个正数。正数的前面可以加上正号“+”来表示。
负数比零小,也比正数小。几何意义上,负数表示在数轴上原点左侧的数,可以用负号“-”标记。
