某航空发动机金属密封环优化设计研究*
2022-07-09赵亚飞潘晨爽杨滢滢励行根
赵亚飞 潘晨爽 杨滢滢 励行根 李 征
(1.中国航发四川燃气涡轮研究院;2.山东大学材料学院;3.上海理工大学;4.宁波天生密封件有限公司)
0 引言
随着科技迅速发展,工业上常用金属密封产品如O 形环、U 形环等在某些场合密封效果并不理想[1],而W 形密封环是近些年开发的一种新型轴向自紧式静密封元件,能适应高温、高压、振动以及强腐蚀的场合[2],有良好的尺寸稳定性,航空发动机中常用其作密封。
本文建立了W 形环参数化模型,为高效处理多因素优化问题,采用数值模拟正交试验法确定主要结构参数用有限元软件对不同参数的结构进行数值计算[3],讨论了主要结构参数对W 形密封环最大Von-Mises 等效应力和上下法兰与W 形环之间的接触应力的影响,保证在最大Von-Mises 等效应力不超过材料屈服极限条件下,获得接触应力的最大值从而保证其密封性能[4]。利用MATLAB 对实验数据进行回归方程拟合计算,通过C 语言编程进行计算优化,最终得到最优结构尺寸。
1 模型建立
W形密封环的密封原理图见图1,由于W形环及其相邻结构具有中心轴对称的特点,可采用轴对称模型进行分析[5]。工作条件为:E面相对于F面的轴向变形量为0.1mm,W 形环内表面所受压力为1.5MPa[6]。为保证密封环与上下法兰之间的接触密封,且密封环不发生断裂事故而泄漏,须计算密封环的压缩应力和密封环与上下法兰之间的接触应力,并与材料的许用应力进行比较,在不超过强度极限时求得最大接触应力[7]。根据材料力学中传统的强度设计方法,对塑性材料,以屈服强度为标准,规定许用应力[ ]σ=σ0.2/n,n为安全系数。在发动机中,对于非叶片类的大多数的金属材料,n>1即可。

图1 W形金属密封环的密封原理图Fig.1 Sealing principle diagram of W-shaped metal sealing ring
对W 形密封环进行结构参数化处理[8-9],如图2 所示,各参数原始取值见表1。为研究其结构对W形密封环综合性能影响的规律,以W环的3个主要结构参数为因素,建立3因素3水平数值模拟正交试验,各主要结构参数水平取值如表2。

图2 W环参数化结构Fig.2 W-ring parametric structure

表1 W环初始结构参数Tab.1 Initial structure parameters of W ring
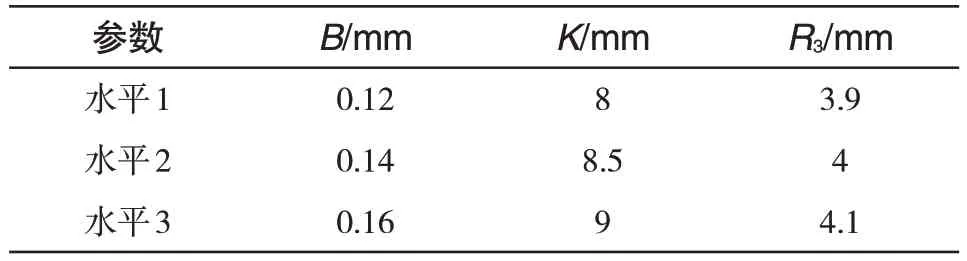
表2 结构参数化Tab.2 The level of structure parameterization
2 计算分析
2.1 模型简化与边界条件设置
首先对模型进行合理的简化与假设,然后给出必要的边界条件。W 环的密封原理见图1,W 环及其相邻结构可采用轴对称模型进行分析;且因与W 环相邻结构的刚性远大于W 环本身,可对相邻部件适当简化。为节省计算量,对模型作如下假设:a)密封环为刚体;b)忽略所有圆角、倒角;c)密封结构及相对位置处于理想状态;d)密封环结构循环对称;e)载荷及边界条件关于中心轴对称[10]。
边界条件如下:约束零件1 固定,零件2 向下移动0.1mm,同时挤压弹性密封环,使弹性密封环产生变形,W环内表面所受压力为1.5MPa。
2.2 材料选择
W形密封环选用高温镍基合金GH4169制造,该合金在高温条件下性能优异[11],其650℃温度下的屈服极限位于高温合金榜首,具有良好的抗氧化、抗疲劳、耐腐蚀性能,以及良好的热加工性、焊接性能和长期组织稳定性,满足密封环工作环境要求。表3 为合金GH4169的相关力学性能参数。

表3 GH4169力学性能参数Tab.3 Mechanical properties of GH4169
优化设计的工况温度为650℃,故参数取值为表3中650℃时的参数值。
2.3 有限元模型建立
利用UG 软件建立参数化W 形金属密封环二维实体模型,结合有限元软件ANSYS Workbench 对W 形环进行有限元分析[12]。
航空发动机中的W 形环的结构和相配合的零件均为轴对称结构,故采用2D 轴对称模型进行分析,划分网格如图3,接触区域设置为摩擦接触,摩擦因数为0.15[13]。对接触区域网格进行细化,如图4。施加轴向位移约束。

图3 模型的网格划分Fig.3 Meshing results of the model

图4 接触区域局部网格的细化Fig.4 Refinement of local mesh of contact area
2.4 数值模拟正交试验计算结果及优化分析[14]
3因素3水平数值模拟正交试验设计的结构矩阵可得到9 种设计组合,每种组合对应一种结构。应用ANSYS软件进行有限元分析,表4为设计变量取值及数值模拟正交试验[15]计算结果。
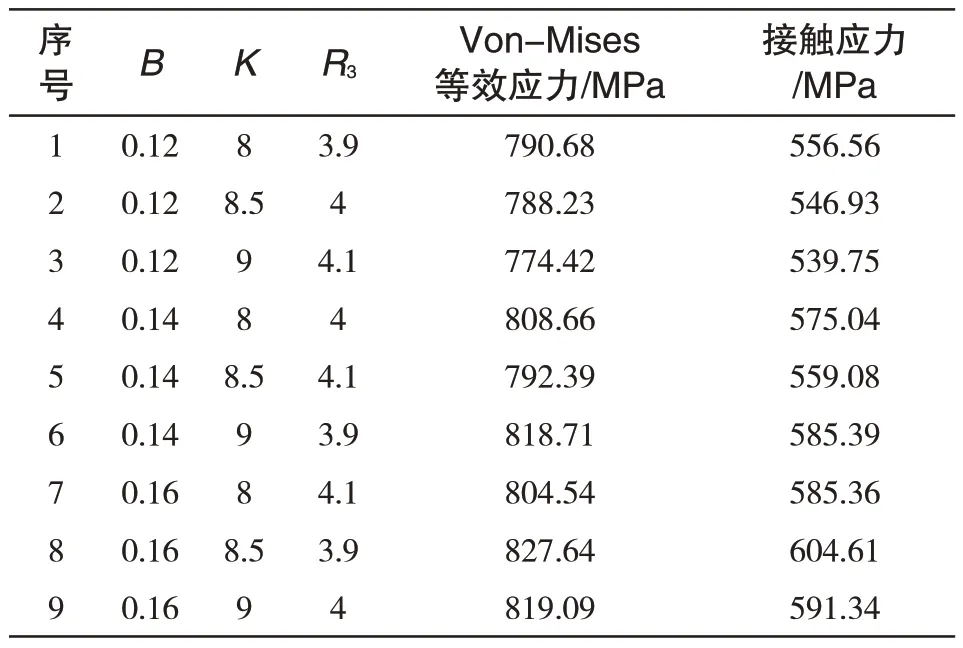
表4 数值模拟正交试验表650℃Tab.4 Orthogonal experiment table 650℃
根据表4中试验结果,应用最小二乘法原理构造正规方程。通过SPSS 软件对试验结果进行回归分析,考虑在5%上显著时,由表5知,壁厚B、接触面曲率半径R3两因素所对应的显著性小于0.05,故B 和R3对Von-Mises等效应力影响显著;由表6可知,B和R3两因素所对应的显著性小于0.05,故B,R3对接触应力值影响显著。为保证回归函数精度,将B和R3与Von-Mises等效应力和接触应力值之间的关系假设为二次关系[16],其方程通式为:
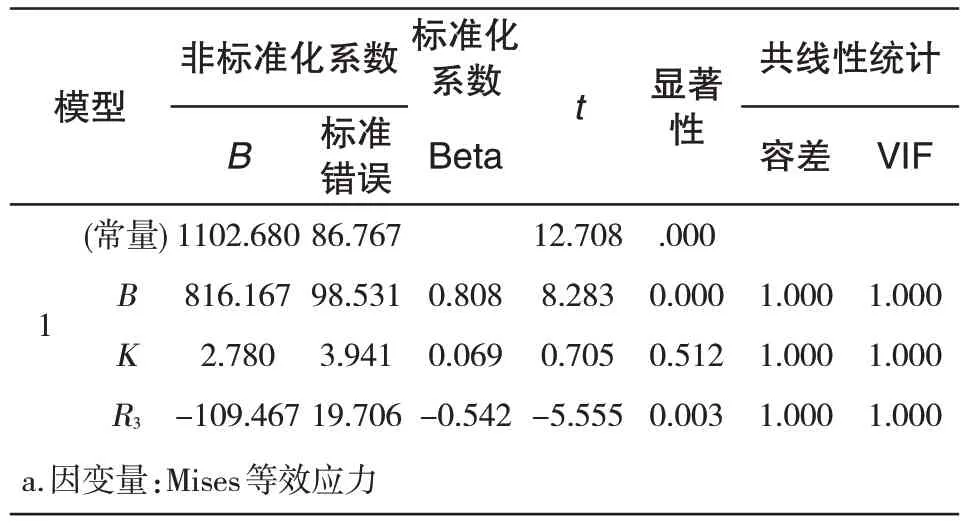
表5 Von-Mises等效应力SPASS分析结果Tab.5 Von-Mises equivalent stress analysis results by SPSS

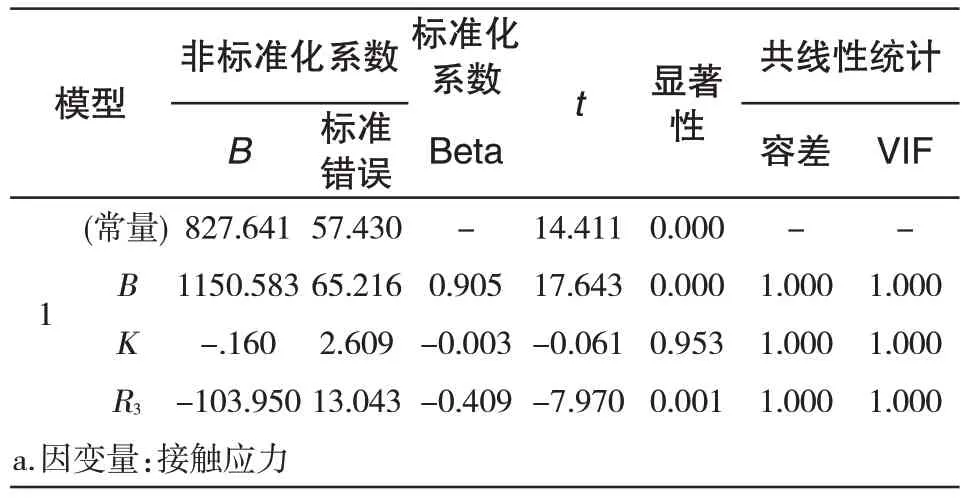
表6 接触应力SPSS分析结果Tab.6 Contact stress analysis results by SPSS
为便于构造正规矩阵,令K=x1,B=x2,R3=x3。则:
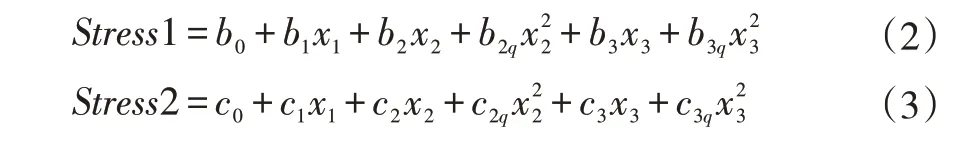
试验结果因素矩阵A,计算结果矩阵B,正规方程组的系数矩阵b,分别表示为:

式中,X为结构矩阵;m=5;n=9;j=1,2,…,9。
则正规方程组可表示为:
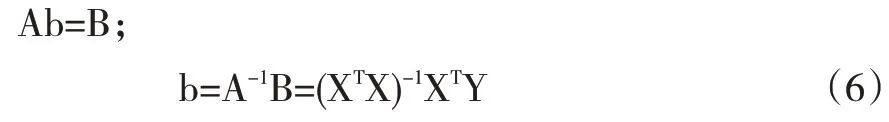
在MATLAB中编写以下程序[17]:

根据程序结果,计算所得Von-Mises等效应力的回归系数见表7,接触应力的回归系数见表8。

表7 Von-Mises等效应力回归系数Tab.7 Regression coefficient of Von-Mises equivalent stress

表8 接触应力回归系数Tab.8 Regression coefficient of contact stress
故Von-Mises等效应力的线性回归方程为:

接触应力的线性回归方程为:
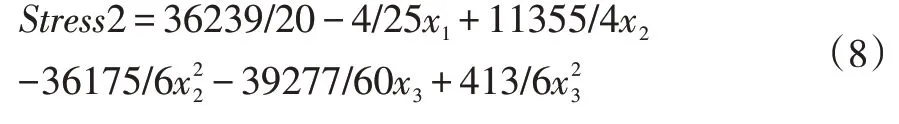
式(8)为接触应力的二次多元线性回归方程,为求最优解,还应保证求得的接触应力最大值时,其参数值对应的Von-Mises等效应力应小于材料屈服极限,优化后结构参数应满足8 ≤x1≤9,0.12 ≤x2≤0.16,3.9 ≤x2≤4.1,考虑加工精度0.01mm,使用C 语言编写以下程序:


3 优化结果及验证
W形金属密封环最优结构参数见表9。

表9 优化后的结构参数Tab.9 Optimized structural parameters
建立B=0.16,K=8,R3=3.9 的W 形环结构,通过ANSYS 软件在预定工况下进行有限元分析。可知接触应力最大值为611.77MPa,仿真结果比表4 中实验最大值604.61MPa 大,且此时Von-mises 等效应力为822.88MPa,未超过材料屈服极限865MPa,表明优化结果较为可靠。优化结构仿真验算的Von-mises 等效应力云图见图5~图6,接触应力云图见图7~图8。

图5 优化的W环Von-Mises等效应力分布Fig.5 Optimized Von-Mises equivalent stress distribution of W-ring

图6 Von-Mises等效应力的局部放大Fig.6 Local magnification of Von-Mises equivalent stress

图7 优化后W形环的接触应力分布Fig.7 The contact stress distribution of the optimized Wring
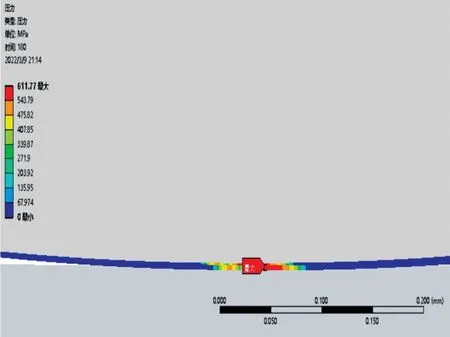
图8 局部接触应力放大Fig.8 Magnified local view of contact stress
4 结论
1)对W形金属密封环进行结构参数化,后以参数组的形式输入有限元软件中分析计算,提高了计算效率。
2)通过建立数值模拟正交试验的方法分析结构参数对应力水平的影响,避免了结构优化的盲目性,通过MATLAB计算得到各应力值同各结构参数的回归方程,将应力结果定量显性化,简化了分析过程。
3)在已知应力值与W形金属密封环各结构参数间的方程关系的条件下,通过C程序设计,得到了结构参数的最优解。将最优解对应W 形环结构通过ANSYS 进行仿真检验,同已进行的数值模拟正交试验结果进行对比,验证了回归方程及优化结果的可靠性。
