基于风电场运行数据的风电功率波动特性研究*

谷晓君 梁 钊 杨昊泽

（1.北京京能清洁能源电力股份有限公司西北分公司；2.华北电力大学新能源电力系统国家重点实验室）

0 引言

近年来，风电迅速发展，风电在电网中所占的容量不断增加[1-2]。风电机组运行于湍流大气中，湍流除了影响机组的运行特性与疲劳载荷等[3]，还会使风电功率的输出具有波动性、随机性及间歇性，这使风电并网应用存在无法满足供电的稳定性与可调性要求、对电网的电压和频率波动存在影响等一系列问题。当风电在电网中的容量占比较大时，会对电网的稳定性产生威胁[4-7]。随着风电在全球能源结构中比重的不断增加，风电功率波动对电网影响的问题也变得愈发重要。因此，对风电波动特性的研究具有很强的必要性，其对于智能电网、储能设备、风电机组控制策略的设计以及区域电网能源配置的规划等都具有重要意义。

目前学术界对风电功率波动已有了一定的认识与研究。风电功率波动由风的湍流波动主导。湍流风的功率谱遵循Kolmogorov谱[8]，即与频率f的-5/3次方和时间尺度τ的2/3次方相关，许多学者已证实，风电机组和风电场功率的功率谱也符合这一规律[9-14]。例如，Milan等[10]证明了风电机组将湍流风转换为具有湍流波动的功率，而在较小的时间尺度上，风电机组的机械惯性会平滑快速的功率波动。由于风的地域差异性，多个风电机组或多个风电场对输入电网的功率波动具有地理平滑作用[13-16]。Katzenstein 等[13]采用功率谱方法分析了多个风电场功率波动间的平滑效应。Bandi[14]通过结构函数方法，研究了大尺度大气流动中风电场间功率输出的相关性及区域内的平滑效应。Milan等[10]则通过概率密度函数法证明了风电场尺度的功率波动依然由大气湍流结构主导，湍流风的间歇性会通过风电机组传递至电网并放大。

总的来说，对于湍流风波动到风电功率波动转换规律的研究具有重要意义，尽管学术界已经进行了一定的相关研究，但基于风电场实测数据的研究仍然较少，而针对国内实际情况的研究更为稀少。为此，本文采用国内现役风电场的实际运行数据，对大气湍流波动到风电功率波动的转化规律开展了研究，分别对风电功率波动的功率谱特性、波间调制作用、间歇性、日变化与年变化规律进行了分析。

本文分析所用数据来自内蒙古克旗一风电场，该风电场由17 台额定功率3MW 的风电机组组成。数据直接取自风电场的数据采集和监视控制（supervisory control and data acquisition，SCADA）系统，包括各个风电机组的输出功率和风速等，采样时间为2017 年5 月到2018 年4 月一年，采样周期为1s。在分析过程中，剔除了因机组故障和传感器故障导致的异常数据，但对实际运行中存在的弃风限电时段数据进行了保留。

1 风电功率的波动特性

1.1 风电功率波动的功率谱特性

在通常情况下，风速到风电机组功率输出的转换可简化为由功率曲线得出。然而功率曲线使用的是平均风速，无法实现短时间尺度的湍流风速到机组功率的动态转换。为了详细探究湍流风波动到风电功率波动的转换规律，可对数据进行频域分析。为此，选取风电场运行数据中长度为一个月且数据完整性较好的一段，通过平均周期图法快速傅里叶变换（fast Fourier transform，FFT）计算风速u、风电机组功率P以及风电场功率Pfarm的功率谱，结果如图1所示，其中虚线为对数坐标系下斜率为-5/3的参考线。

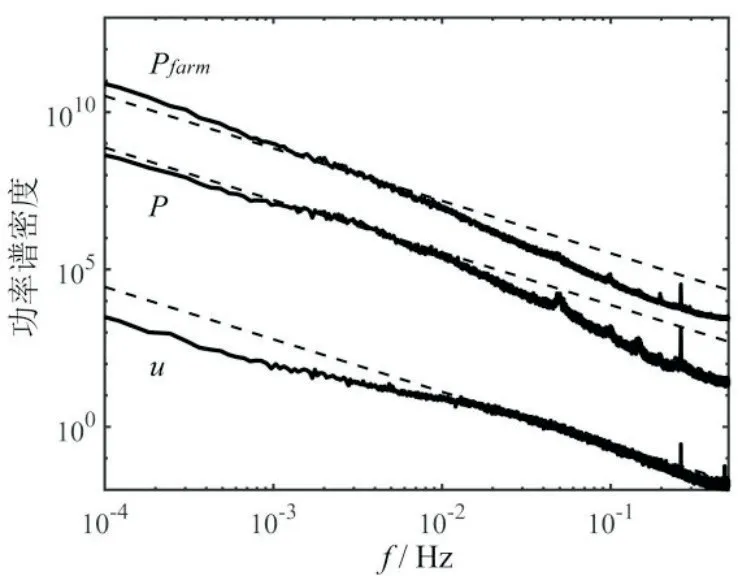
图1 各数据的功率谱Fig.1 Power spectrum of the data

可以看出，风速基本上符合Kolmogorov的“-5/3”定律，即功率谱S(f)～f-5/3，与高雷诺数下的壁面湍流特性一致。在f＜0.01Hz的低频段，风速的功率谱平坦化，这一现象也在参考文献[9-10]中被观察到。在该低频段内，单台风电机组功率的功率谱也符合“-5/3”定律，这说明在该时间尺度上，机组功率符合湍流的基本特性，存在风速波动到功率波动的直接转换。在f＞0.01Hz 的高频段，机组功率的功率谱偏离“-5/3”定律，原因在于机组的传动系统机械惯性与控制策略使低于机组反应时间的快速风速波动被过滤，该反应时间取决于机组的具体设计、尺寸和运行环境等诸多因素，在此不再作进一步分析。风电场功率的功率谱特征与风电机组功率的功率谱基本一致，其中f＞0.01Hz 高频段功率谱的偏移也可能与多个风电机组在空间上的平滑效应有关。总的来说，对于大、中时间尺度，风电机组和风电场的功率波动都由湍流风的波动特性主导，需要特别关注；而小时间尺度的功率波动受机组运行特性影响，波动程度有所降低。

1.2 风电功率波动的波间频率调制作用

多重分形特性是湍流的主要特征之一[17]。Huang等提出的经验模态分解方法（empirical mode decomposition，EMD）[18]可以有效地将信号数据分解为有限个固有模态函数（intrinsic mode function，IMF）之和，从而提取数据在各个尺度上的结构特征。本文采用经验模态分解方法对风电功率波动进一步分析，出于篇幅考虑，在此不对该方法的具体步骤及公式进行介绍。

选取长度为8小时的连续数据，对风速和风电机组功率分别进行经验模态分解，两者各分解为14和12个IMF，结果如图2 所示（图中仅展示奇数IMF）。可以看出，风速序列存在明显的多重分形结构与间歇性特征，并且各个风速分量间具有显著的波间频率调制作用，即各分量的变化之间存在一定的相关性，这一规律符合湍流风的基本特征。风电机组功率序列的分量虽然存在一定的数值突变，但仍可以观察到较为明显的多重分形特性、间歇性以及波间频率调制作用，并且具有调制作用的频段与风速一致。以上结果再次说明在多个时间尺度上，风电机组的功率波动皆由湍流风波动主导。

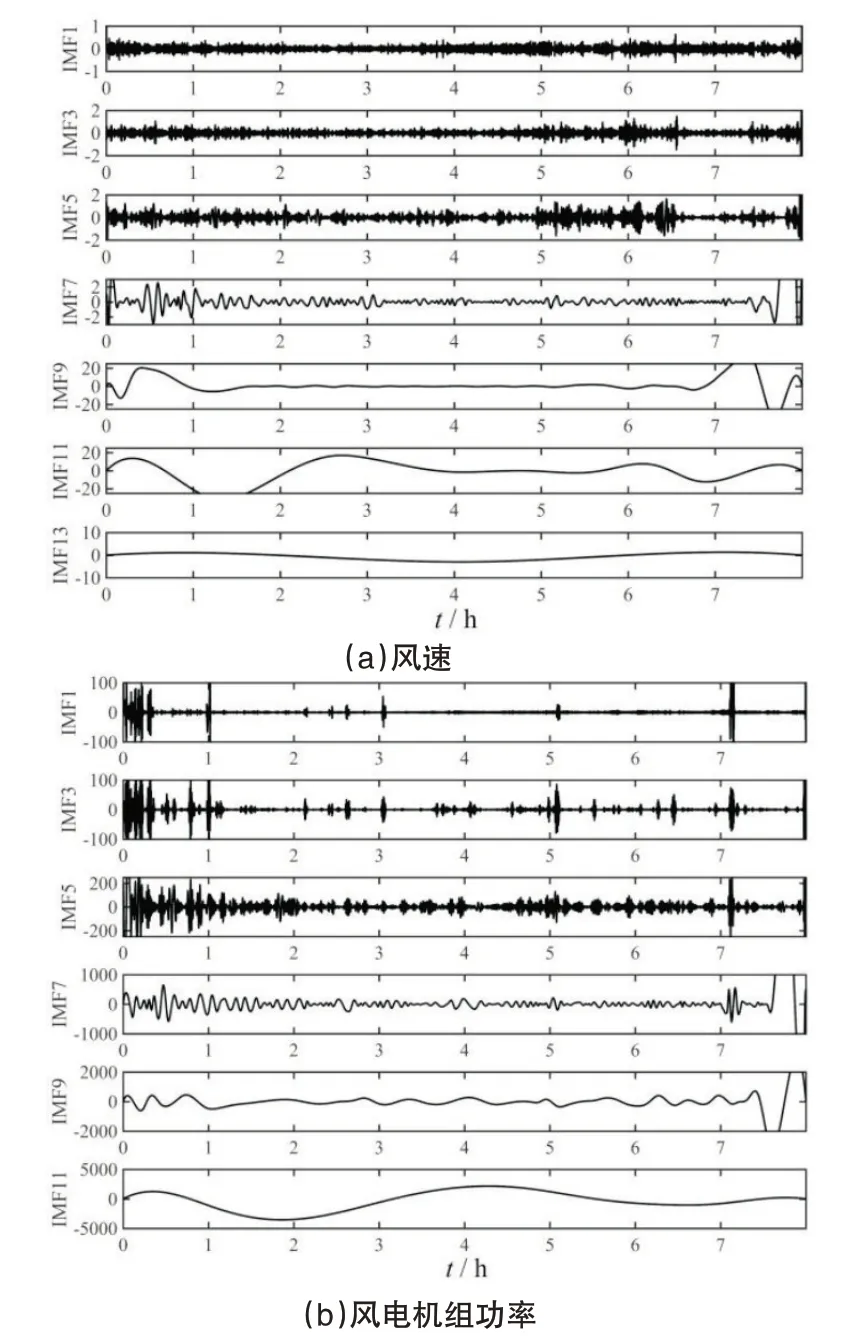
图2 各数据的经验模态分解结果Fig.2 Empirical mode decomposition results of the data

2 风电功率波动的间歇性

许多研究已证实，湍流具有间歇性。湍流的间歇性可以通过一些统计特征量量化，例如，空间或时间上的湍流速度差具有非正态的概率分布。根据中心极限定理，一个完全随机的均匀各向同性湍流应该具有正态的概率分布，因此湍流流动的统计特性偏离正态分布正是间歇性的表现。

为了验证风电功率间歇性与湍流风间歇性的关系，本文采用概率密度函数（probability density function，PDF）对间歇性进行量化表现。使用风速增量表示风速u在时间尺度τ上的变化，计算式为uτ(t)=u(t+τ)-u(t)，进一步计算uτ的概率密度函数f(uτ)。使用相同方法计算对应风电机组功率的增量概率密度函数f（Pτ）和风电场总功率的增量概率密度函数f(Pfarm,τ)。为研究小时间尺度的快速风速波动对功率的影响，选取τ为8s，对长度为一个月的数据进行增量概率密度函数计算，结果如图3 所示，其中虚线为作为对比的标准正态分布。为便于概率密度函数的观察与比较，使用各函数的标准差στ分别对x坐标进行了标准化，并将曲线在纵向上进行了平移处理。结果显示风速、单个风电机组功率以及风电场总功率的增量概率密度函数都明显偏离了标准正态分布，存在指数型的厚尾，对应数据中的极端事件。根据偏离正态分布的程度，可认为风速中度间歇，风速信号中记录的极端事件可达10στ；而风电功率高度间歇，单个风电机组和风电场功率信号中记录的极端事件分别可达30στ和20στ。这说明湍流风的间歇性会被风电机组传递到功率输出上。

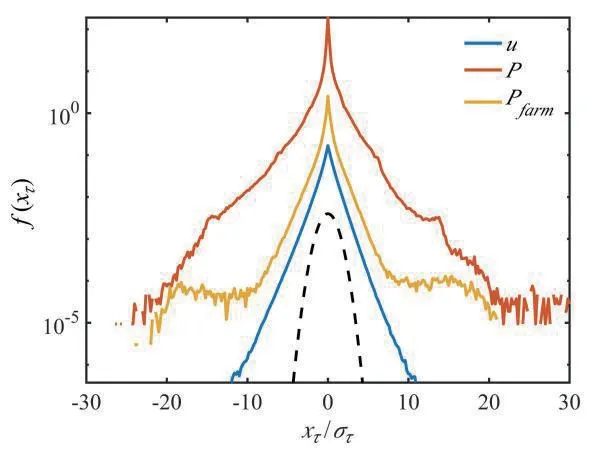
图3 各数据的增量概率密度函数Fig.3 Probability density function of the data

进一步采用增量概率密度函数的平坦度量化间歇性的大小，计算式为随机变量的4阶中心矩与方差平方的比值：

对于标准正态分布，F(τ)=3。经过计算，上述风速、单个风电机组功率及风电场总功率增量概率密度函数的平坦度分别为8.2，42.4，66.3。与湍流风相比，风电功率的间歇性显著提高。可见，一方面，湍流风的间歇性在传递至风电机组功率上时有所提高；另一方面，风电间歇性存在于整个风电场尺度上，即多台风电机组的功率波动汇集到电网时不会完全被平均，甚至有可能被放大。这是由于在占地面积较小的风电场内，各风电机组的来流风相似，因此，功率波动也呈现正相关规律，类似的现象也在参考文献[10]中被观察到。除此之外，根据对|Pfarm,τ/στ|＞10 的极端情况数据的分析可以发现，该类数据中非正常运行状态（弃风限电、故障停机等）数据占大多数，在该状态下，各个机组的功率波动也具有很强的正相关性，这导致了风电场功率的大幅波动，进一步增强了风电场功率的间歇性。

3 风电功率波动的日变化与年变化规律

上述研究揭示了较短时间尺度的风电功率波动规律，而在大、中时间尺度上，大气边界层的湍流风具有明显的日变化、年变化规律，这一规律也应转移到风电功率波动上。

采用脉动速度的均方根值，对湍流风的波动强度进行量化表述，计算式为：

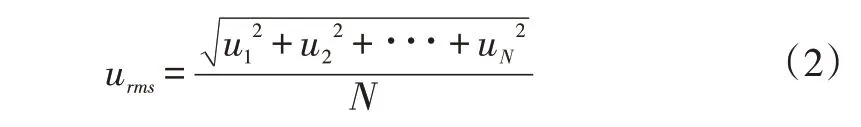
式中，u为平均风速与瞬时风速的差值，代表脉动风速。对于风电机组以及风电场功率，也采用相同方法求取均方根值。

3.1 日变化规律

筛选每个季节数据完整性较强的5到10天的数据，对筛选出的数据求取每分钟的平均风速、脉动风速以及每小时的均方根值，风电机组以及风电场功率的均方根值也采用相同方法计算。在结果中，各个季节的小时均方根值都表现出相似的规律，为了便于观察，对所有结果作平均化处理，得到全年平均的24 小时每小时均方根值，结果如图4 所示。可以看出，风速和风电功率的24 小时均方根值都存在明显的峰谷值，说明两者都具有明显的日变化规律。风速波动在夜间较低，在约5时为最小值，在清晨和上午上升，在约15时达到最大值，并在下午和傍晚下降，以上结果与大气边界层中湍流强度的日变化规律基本一致。风电机组和风电场的功率波动也基本符合这一日的变化规律，这说明在小时级的时间尺度上，大气湍流风的波动会传递到风电功率波动上。

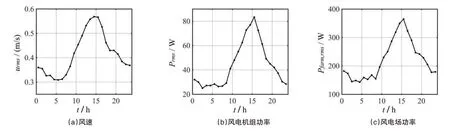
图4 24小时每小时各数据的均方根值Fig.4 Data's root mean square per hour

3.2 年变化规律

对上述每个季节的数据集分别求取24小时平均每小时均方根值，以分析风电功率波动的年变化规律，结果如图5所示。风速波动具有明显的年变化规律，春季风速波动最大，其次分别是冬季、夏季和秋季。此外，秋季最大值时间段稍早于其他三个季节，春季最小值时间段稍早于其他三个季节。以上现象基本符合风电场所处位置的内蒙古温带大陆性季风气候的特点，即大风、多风天集中在春、冬两季。风电机组和风电场的功率波动变化规律虽然在趋势上与风速波动略有不同，但也基本符合以上年变化规律，这说明在大时间尺度上，风电功率波动具有与大气湍流风波动相同的规律特性。

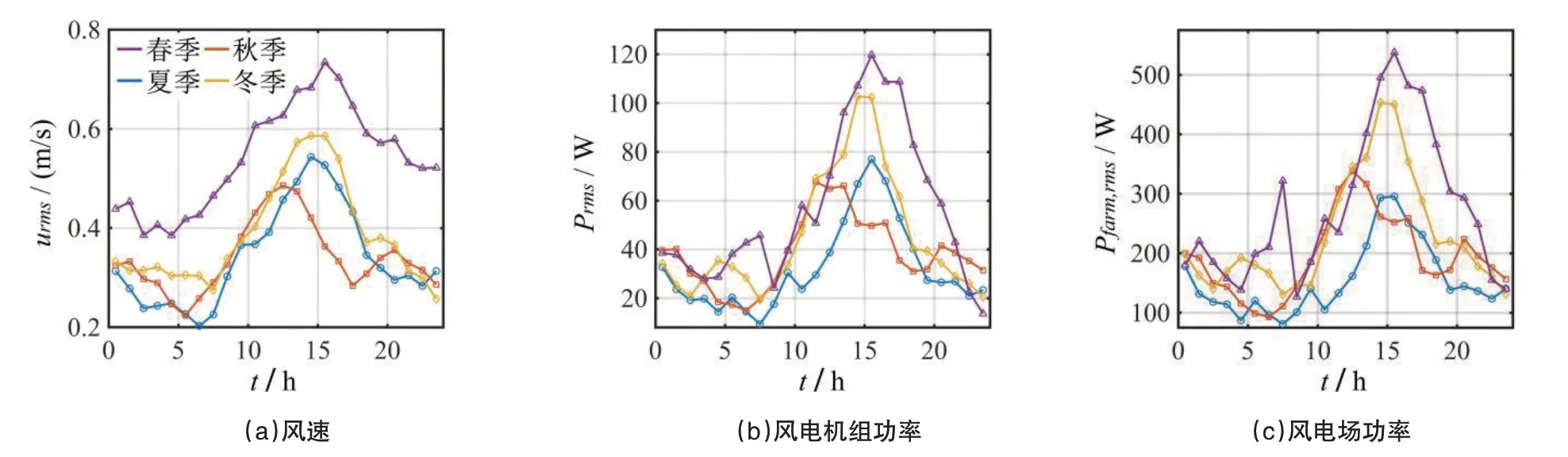
图5 各数据在各季节中24小时每小时均方根值Fig.5 Data's root mean square per hour in each season

以上结果说明了在小时级和月级的时间尺度上，大气湍流风的波动特性也会完整地传递至风电功率波动上。因此，通过测量大气湍流度的日变化、年变化规律，即可提前预测风电功率波动的日变化、年变化规律，为风电场设计规划提供参考。

4 结论

风电功率具有显著的波动特性，为风电大规模并网带来了挑战。然而目前基于实测数据，特别是针对国内实际情况的相关研究仍然较少。为此，本文采用内蒙古克旗一现役风电场的实际运行数据，对各个时间尺度上大气湍流波动到风电功率波动的转换规律开展了研究，主要结论如下：

1）在f＜0.01Hz 的低频段，风电功率的功率谱符合Kolmogorov 的“-5/3”定律，此时风电功率波动由湍流风的波动特性主导；在f＞0.01Hz的高频段，风电功率波动受机组运行特性影响有所降低。

2）通过经验模态分解，发现风电功率序列分量上存在多重分形特性、间歇性以及波间频率调制作用，与湍流风的基本特征一致。

3）风速、风电功率的增量概率密度函数都偏离标准正态分布，且风电功率的偏离程度更大，说明风电机组可以传递湍流风的间歇性并将其放大。在多台机组的功率汇集至电网时，由于各机组来流风的正相关性，功率的间歇性可能被再次放大。

4）风电功率波动与大气湍流风波动具有相同的日变化和年变化规律，大时间尺度的湍流风波动特性会完整地传递至风电功率波动上。

本文基于风电场运行数据，对风电波动特性的研究具有一定的实际应用价值，可为智能电网、储能设备、风电机组控制策略的设计以及区域电网能源配置的规划等提供重要参考。

致谢：本工作由国家自然科学基金12172128资助，感谢华北电力大学葛铭纬教授的指导，感谢北京京能清洁能源电力股份有限公司提供的风电场运行数据。