风剪切与平台纵摇对漂浮式风电机组气动失谐的影响*

2022-07-09郭翼泽王晓东潘其云娄刻强郭小江

风机技术 2022年3期

郭翼泽王晓东潘其云娄刻强郭小江

（1.华北电力大学电站能量传递转化与系统教育部重点实验室；2.华能集团清洁技术研究院有限公司）

1 概述

风电是清洁的可再生能源，具有大规模的开发潜力。相较于陆上风电，海上风电不受地形限制，并且拥有更丰富的风资源。漂浮式海上风电机组（FOWT）大部分时间运行环境复杂，产生六自由度（6-DOF）运动，如图1所示，有三个平移分量，即沿Y方向的垂荡、X方向的横荡和沿Z方向的纵荡，以及三个旋转分量，即围绕X轴的纵摇、围绕Y轴的偏航和围绕Z轴的横摇。漂浮式海上风电机组六自由度运动引起风轮相对风速改变，导致机组三个叶片受力不均，破坏风轮原有的协调性，造成风电机组气动失谐。海平面空间宽阔，没有山丘等高低地形变化，受海平面摩擦力影响，风剪切效应显著，叶片运动到不同高度具有不同风速。风速的变化使机组各叶片上的荷载不同，风电机组气动失谐增加。随着漂浮式风电机组大型化，风剪切以及平台多自由度运动对漂浮式风电机组产生的影响也逐渐增大。研究风剪切来流与平台运动条件下机组的气动特性，对漂浮式风电机组安全稳定运行具有指导意义。

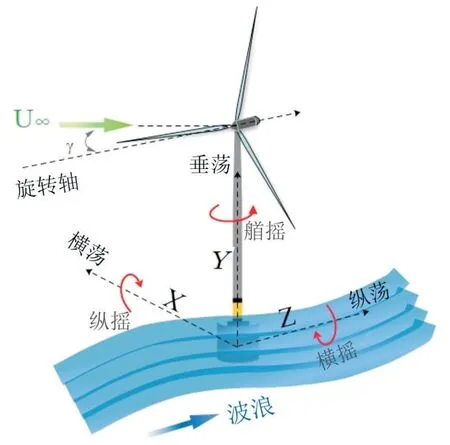
图1 浮式平台在风浪流作用下的六自由度Fig.1 6-DOF of the platform under wind wave and current

许多学者对风剪切条件下风电机组的气动性能做了研究，陈福东等[1]使用大涡模拟（LES）与致动线方法（ALM），研究风剪切且风电机组有一定俯仰角时的气动性能，以及其尾流对下游风力机的影响。结果表明随着俯仰角的增大，上游机组的功率先增后减，下游机组功率持续增加。许波峰等[2]使用自由涡尾迹（FVW）方法，研究剪切风造成的气动载荷与尾迹形状变化，结果表明剪切因子使尾迹倾斜程度增大，且气动力系数周期性波动的幅度最大，风力机的总体性能降低。陈晓明[3]分析了不同风速廓线指数和展向位置处风剪切的影响规律，指出风剪切使得风力机性能、载荷和流动参数波动振幅增大，随方位角呈近似余弦函数型式的周期性波动，波动波幅随风速廓线指数和展向位置而增加。仇永兴等[4]研究发现风切变条件下，叶片安装角存在偏差的失谐风轮的俯仰、偏航力矩波动较大。陈子文等[5]基于计算流体力学（CFD）方法研究了风剪切系数为0.1时，风剪切来流与浮式平台运动纵摇和纵荡运动耦合对NREL 5MW机组的气动性能与扰流细节的影响。结果表明风剪切使机组平均发电量降低，加剧载荷的波动。Yang Zhou 等[6]采用CFD 方法研究了风剪切对漂浮式风电机组总体性能的影响，发现较大的风切变层厚度会导致局部功率的突然下降。王鹏等[7]基于工程尾流模型，提出风电场尾流模型，对风电场尾流平均风速有较好的反映。

一些研究关于浮式平台在风浪流耦合作用下产生的六自由度运动对风电机组气动性能影响。直接采用大型风电机组进行实验非常困难。许多研究人员利用缩比模型和人工水池研究其六自由度运动特性。Bachynski[8-9]将5MW 的漂浮式风电机组与OCO 平台结合，在波浪水池中测试其平台运动的衰减特性，并使用了一种叫做"实时混合模型测试(real-time hybrid model testing)"的方法。该方法中，风电机组的瞬时功率和推力是由结合实验测量的平台运动的机组数值模拟得到，而不是由缩比后的叶片直接产生[10-13]，结果具有高度的可重复性。他们发现在规则的波浪下，空气动力载荷对平台运动的影响很小，而不规则波和湍流风会引起平台的显著运动。更多的研究都是基于模拟方法，快速计算的方法主要是基于叶素动量理论（BEM）与自由涡方法（FVM），Tran 和Kim[14]使用非稳态叶素动量理论（UBEM）和计算流体力学（CFD）方法研究了平台纵摇运动对FOWT的影响。研究结果显示，由于理论上的限制，UBEM方法的准确性较低。FOWT的空气动力性能对纵摇幅值和频率的变化很敏感。Wen等[15-17]使用FVM 方法研究了平台纵摇运动下FOWT 的气动性能。比较了纵摇和非纵摇情况，以及不同的纵摇幅度和频率。随后，他们提出了一个无量纲数折合频率（reduced frequency）K来表示纵摇幅度和频率的综合影响。功率受K和叶尖速比λ的影响。当K增加时，平均功率输出在低λ时减少，但在高λ时增加。使用CFD方法研究平台运动下漂浮式风电机组的气动性能波动的研究并不多，白雪峰等[18]使用自由涡尾迹法模拟NREL 5MW风电机组在纵摇，纵荡和横摇下的气动性能，结果表明平台纵摇影响最大，横摇最小，且耦合运动显著增加平均发电量。Wang 等[19-20]提出一种双滑移网格法构建多自由度流体计算域，用来模拟平台运动下的气动性能，研究了Phase VII风电机组在静态与动态偏航条件下的非稳态气动性能。结果表明在10°、30°和60°的偏航角下，平均功率和推力明显下降。此外，动态偏航可以增加沿偏航轴的速度，导致功率系数比静态偏航情况时的更大，之后又研究了NREL5MW在平台纵摇与横摇运动[21]，平台纵摇与纵荡运动[22]下的气动性能，结果发现平台纵摇对功率和推力的影响比横摇的影响要大得多，而平台横摇的影响可以忽略不计，纵摇与纵荡的耦合运动会减小漂浮式风电机组的平均功率。

目前使用CFD方法对比剪切风来流与浮式平台运动，对漂浮式风电机组气动性能影响的研究还比较少，文中选择风剪切系数0.2，0.3，浮式平台典型运动纵摇运动，与均匀来流下平台固定工况比较，研究两者对风电机组气动性能的影响。

2 计算模型与数值方法

2.1 计算模型

NREL5MW数字参考样机为三叶片风电机组，风轮直径126m，叶片长度61.5m，轮毂高度约为90m，叶片由DU 和NACA 系列翼型组成，本文中建立的风轮计算模型，将轮毂和机舱简化，忽略塔架的影响。额定风速为11.4m/s，额定转速12.1r/min。

2.2 CFD计算方法

计算域如图1 所示，流场分为四个区域，分别是远场域、平台平动域、平台角运动域和旋转域。远场域是长方体，长14D，宽12D，高12D，其中D是风轮直径，风轮距进口和出口的距离分别为6D和8D。旋转域直径1.5D，宽度30m。平台角运动域的中心设在轮毂高度以下90m，直径4D，平台平动域为正方体，边长5D。

图2 计算域Fig.2 Computational domains

2.2.2 网格

网格使用Fluent Meshing生成。远场域和偏航域采用四面体-六面体混合方法生成面网格和体网格。远场域网格253 万，平动域网格92 万，角运动域网格65万。旋转域为全四面体网格，网格数量1377万。

图3 风轮网格Fig.3 Computational mesh

2.2.3 网格无关性验证

表1 展示了在均匀风11.4m/s 平台固定工况下，四种不同网格数量分别进行稳态计算得到的扭矩，网格数分别为1000 万，1246 万，1377 万，1600 万，额定风速下的设计扭矩为4.08×106Nm，将设计扭矩作为参考值。结果表明，风轮网格数1377万时，计算结果与设计值差距较小，所以进一步研究风轮均采用1377万网格。

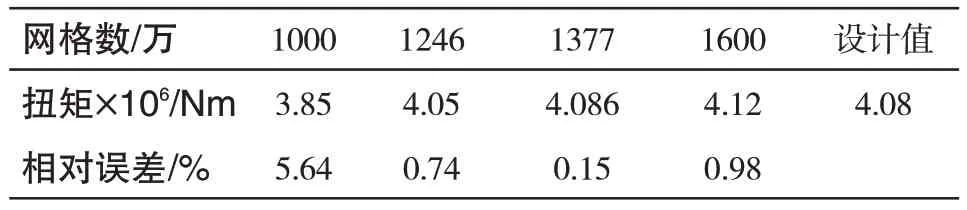
表1 不同网格数下的计算扭矩Tab.1 Torque of different grid sizes

2.2.4 边界条件

进口采用速度进口边界，上下表面为自由无滑移边界条件，叶片和轮毂设为无滑移壁面，出口边界为压力出口，转速为12.1r/min，来流为均匀风时，设定额定风速11.4m/s，来流为剪切风时，进口风速廓线为指数分布由以下公式给定

牛皮糖被这个家伙的奇谈怪论逗得笑起来。后来指着走远的村长背影说，他说你写了一篇文章，把书记弄得不快活。

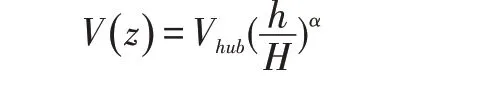
其中，Vhub为轮毂处来流风速，取11.4m/s；V(z)为海平面高度方向h米处的风速；H为轮毂距离海平面高度；α取0.2和0.3。风速廓线如图4（a）。

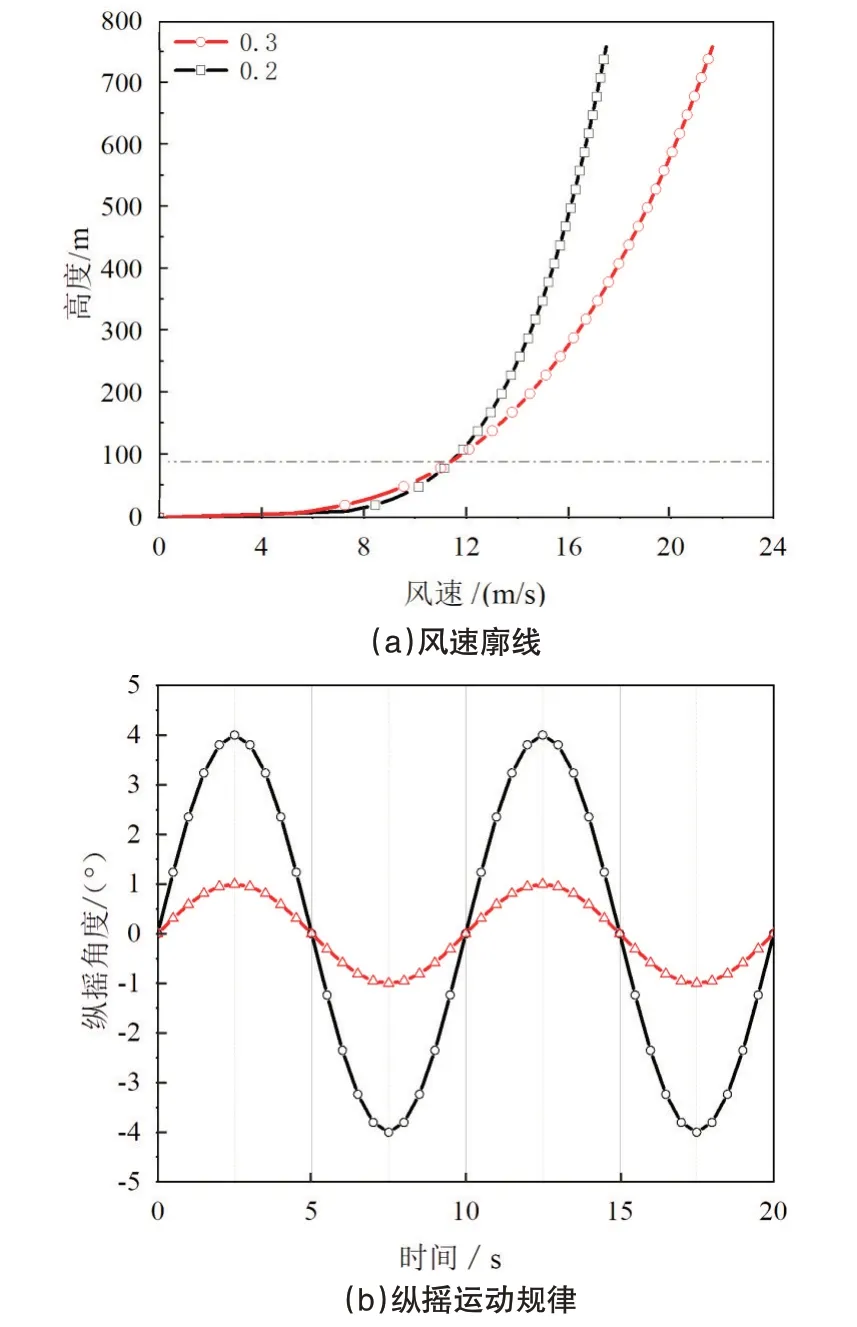
图4 风速廓线与纵摇运动规律曲线Fig.4 Wind speed profile and platform pitch setting

纵摇运动以轮毂高度下方90m处为圆心，是沿来流方向的前后旋转角运动，将其简化为正弦运动，运动的定义为：

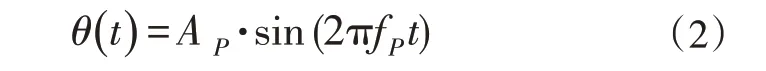
其中A P为纵摇运动的最大角度，fP是运动频率。纵摇运动的位移如图4(b)，纵摇运动的角速度可以定义为：

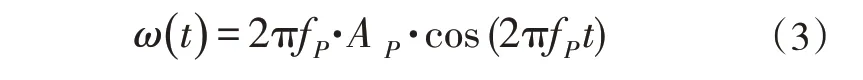
本文主要研究的工况见表2。

表2 计算工况Tab.2 Calculation conditions

2.2.5 计算设置

使用Fluent 求解URANS 方程，湍流模型选择Transition SST。使用滑移网格方法设置风轮的旋转和纵摇运动。等非定常计算收敛平稳后，取最后四圈结果进行分析。

3.1 气动性能

从总体性能的变化曲线（图5）与极值和平均值直方图（图6）可以看出，对比额定风速11.4m/s，平台不运动时，浮式平台纵摇运动使风电机组的功率和推力发生剧烈波动，幅值1°时，功率的最大值是最小值的1.61倍，当功率增加到4°时，波动更加剧烈，其功率的最大值是最小值的7.37倍。推力与功率的变化趋势相似，但是波动范围稍微减小。平均功率随纵摇运动幅值的增加而增加，而平均推力在幅值1°时最高，运动幅值为4°时平均推力降低，与平台不运动工况几乎相等。

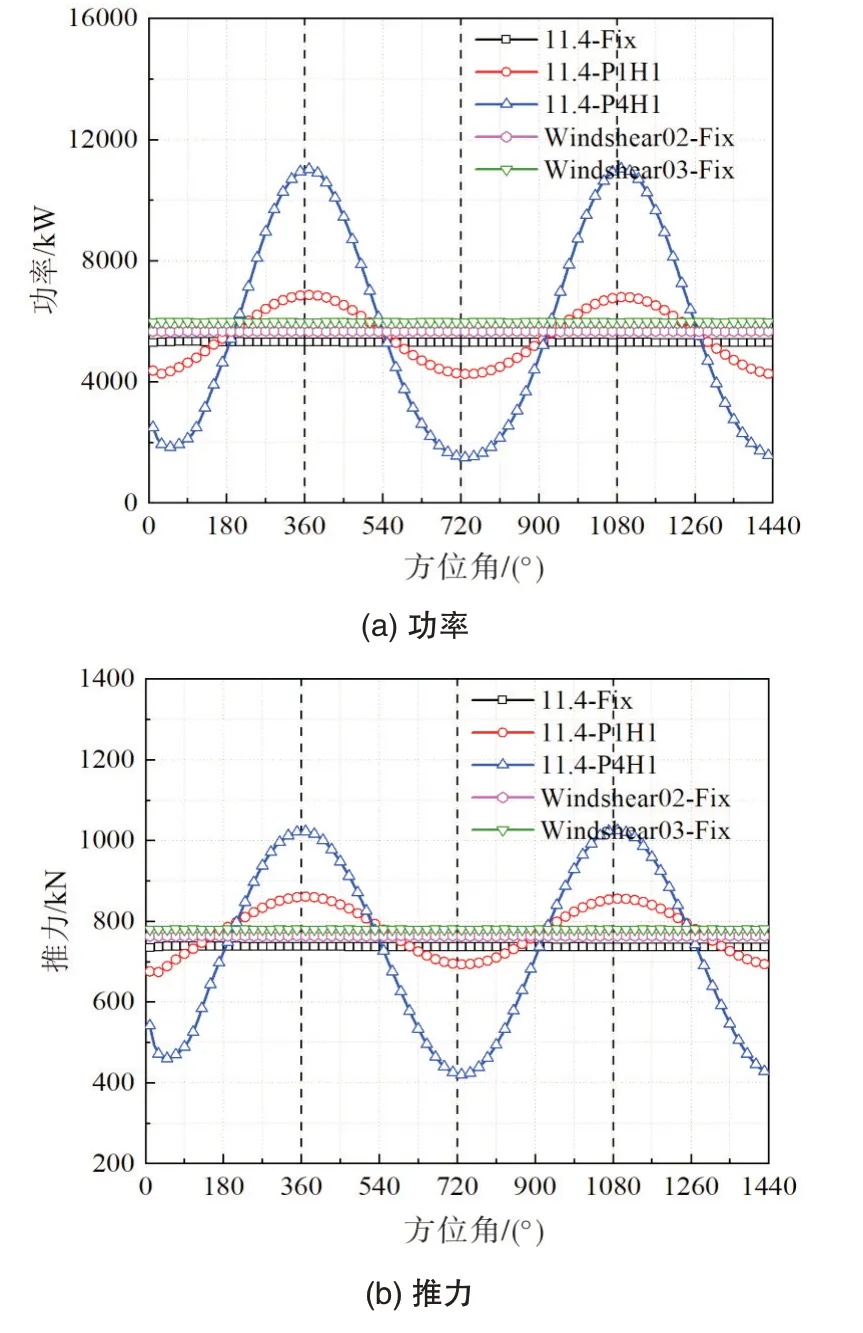
图5 漂浮式风电机组在不同条件下的气动性能Fig.5 Aerodynamic performance under different conditions

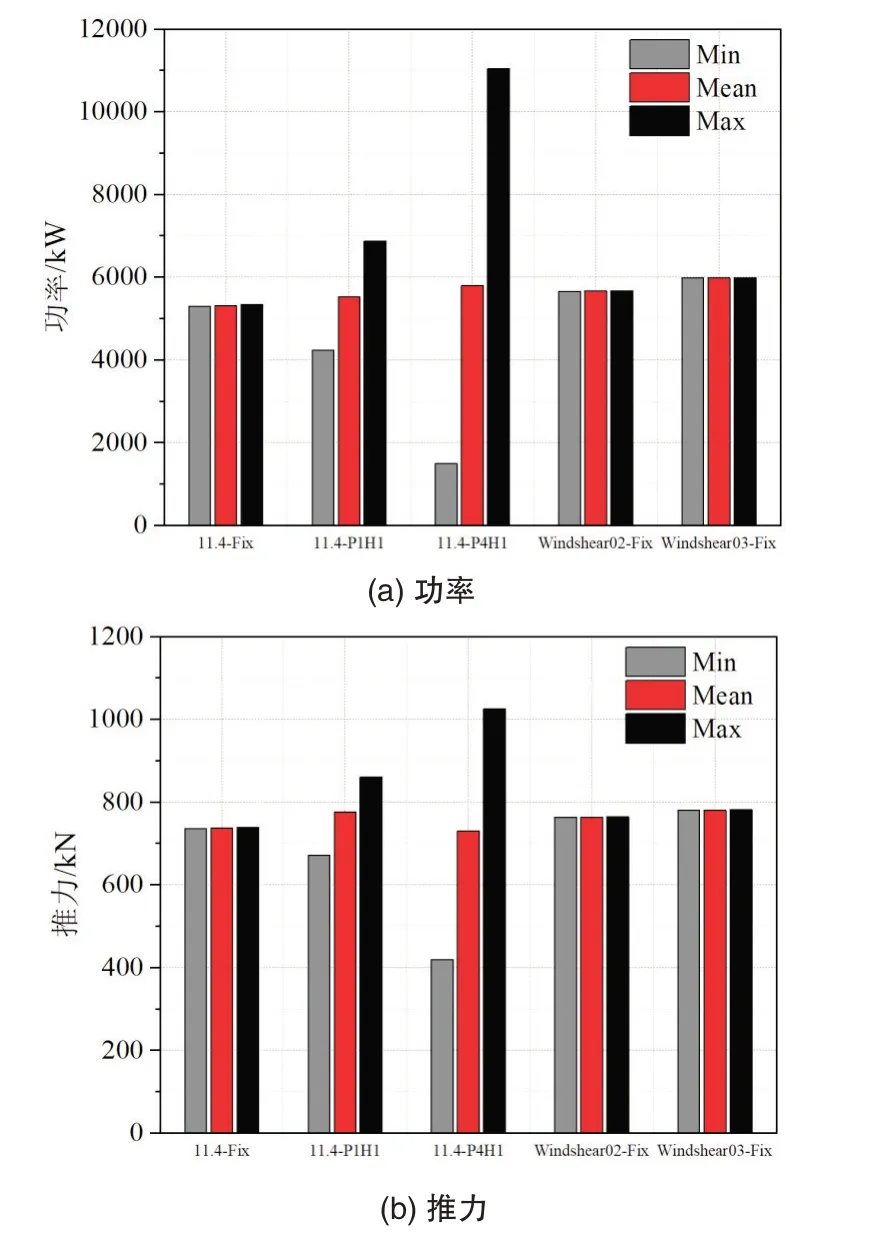
图6 漂浮式风电机组平台运动与风剪切时的总体性能极值与平均值Fig.6 Extreme and average values at wind shear and platform pitch of FOWT

风剪切来流且平台固定时，风电机组的功率和推力波动较小，与额定风速工况相比小幅上涨。随着风剪切系数的增加，风轮顶部风速增加，底部风速降低，平均功率和推力也逐渐增加。说明风轮对高风速较敏感，风速的提高使功率和推力增加。

3.2 截面气动载荷

浮式平台纵摇运动与风剪切来流增大了漂浮式风电机组运行中的不稳定性，导致沿叶展高度不同位置处的载荷与额定风速时不同。取展向不同高度0.21R，0.4R，0.67R，0.96R，研究平台纵摇与风剪切导致的不稳定对截面气动载荷的影响，多个工况下在这四个展向位置的截面Cn与Ct如图7和图8。

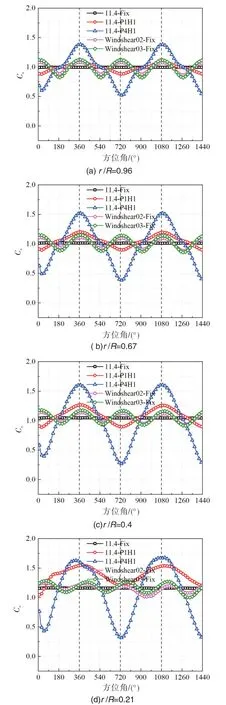
图7 漂浮式风电机组平台运动与风剪切时不同叶展高度的CnFig.7 Cn at different spanwise sections for wind shear and platform pitch of FOWT

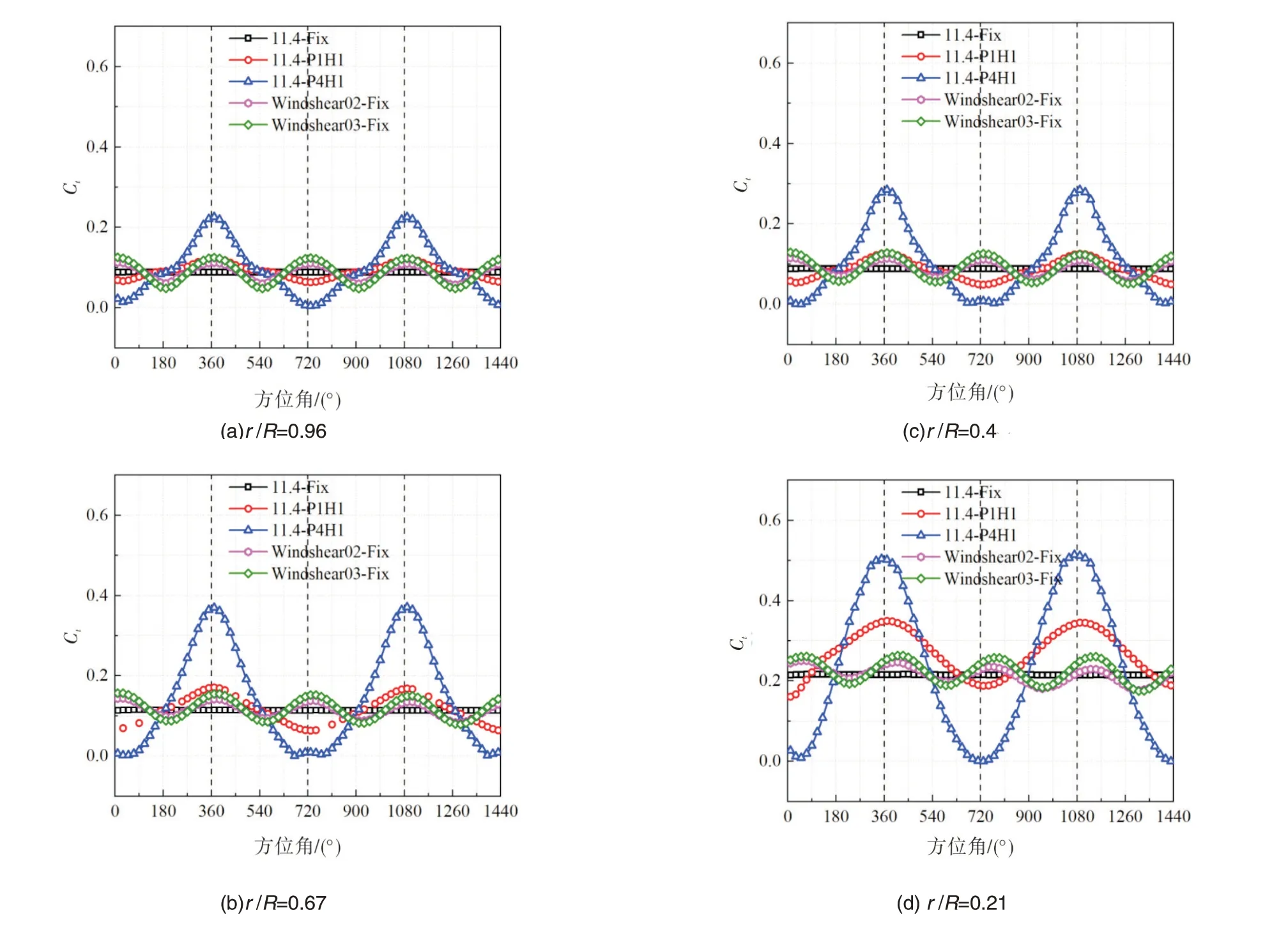
图8 漂浮式风电机组平台运动与风剪切时不同叶展高度的CtFig.8 Ctat different spanwise sections for wind shear and platform pitch of FOWT

在来流为额定风速且平台不运动时，不同叶展高度截面的Cn与Ct都保持稳定，在四个旋转周期中都没有波动，中外叶展（0.96R，0.67R，0.4R）Cn都约为1，Ct约为0.1。内叶展（0.21R）的Cn，Ct略高，Cn为1.16，Ct为0.21。

平台纵摇时Cn与Ct波动剧烈。其中幅值的增加使Cn与Ct在各个叶展位置的波动比幅值较低时更剧烈，导致叶片表面承受频繁剧烈变动的载荷，容易造成叶片的疲劳损伤。从外叶展到内叶展，曲线的波动幅度逐渐增加，内叶展承受更大的交变载荷。因此在浮式平台纵摇过程中需要避免大幅值的运动，以及要注意内叶展的状态，避免叶片疲劳载荷造成机组的重大事故。

根据2.1 中的分析，风剪切系数0.2 与0.3 使风电机组的总体性能增加。剪切来流使叶展高度的截面载荷发生波动，剪切风沿高度方向有速度梯度，当叶片从较高风速处旋转到低风速高度，叶片表面载荷发生变化。风剪切对外叶展的影响较大，对内叶展的影响较小。在外叶展，风剪切造成的波动与纵摇1°，0.1Hz 造成的载荷波动相当，但是曲线的波动频率较高，以风轮旋转一圈为周期，频率约为0.2Hz。

3.3 旋转平面气动载荷

图9 和图10 为单个叶片在一个旋转周期内Cn与Ct变化。来流为额定风速，平台不运动时，叶片旋转一周的Cn与Ct在叶根处较大，Cn在外叶展最低，Ct在0.6R到0.8R最低。在旋转一周过程中，各个展向位置波动较小。

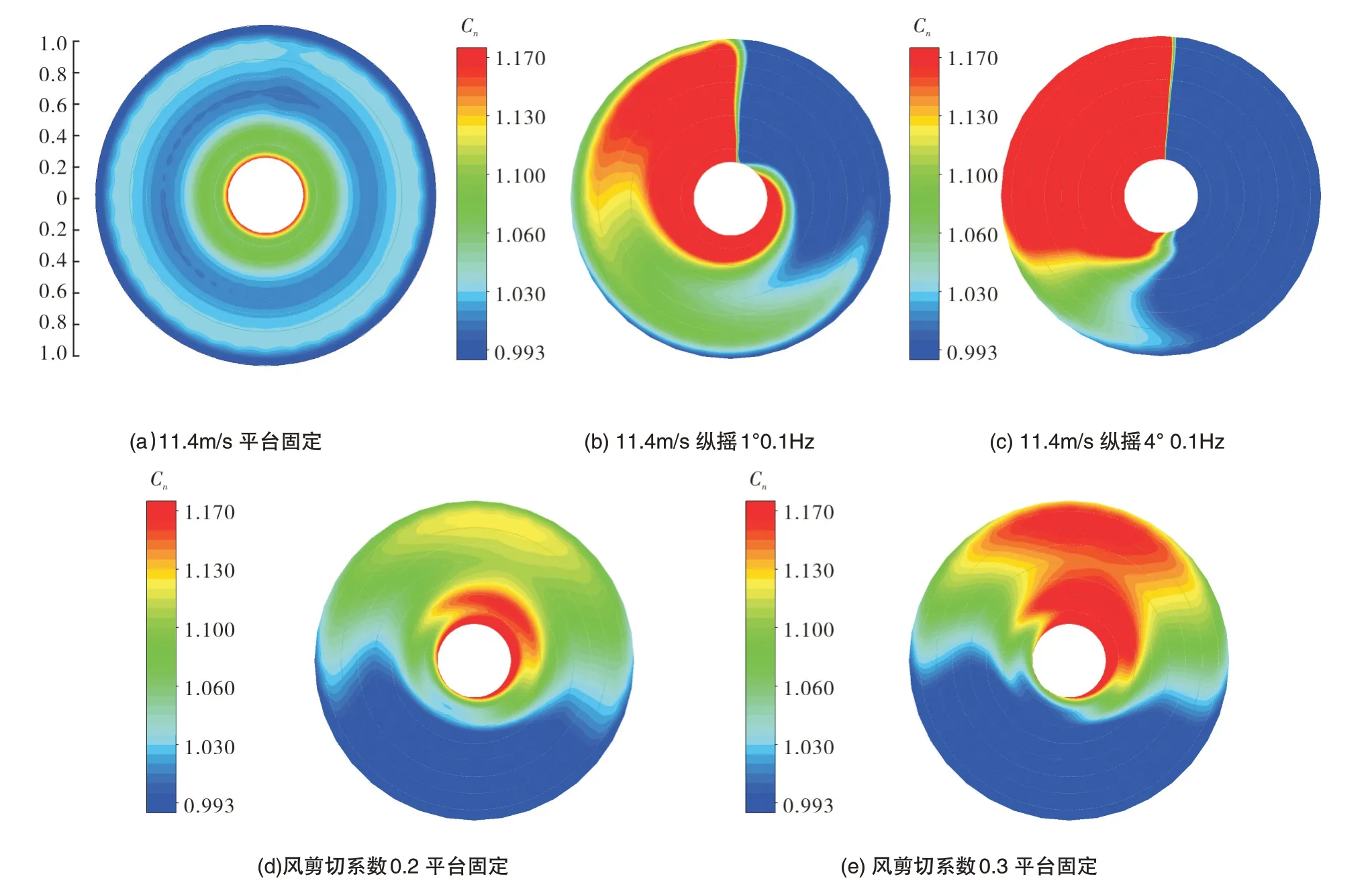
图9 单个叶片Cn在旋转平面的分布Fig.9 Distribution of Cn blade in the rotation plane

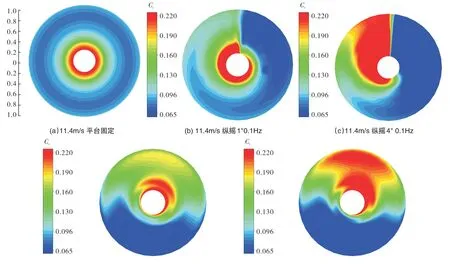
图10 单个叶片Ct在旋转平面的分布Fig.10 Distribution of Ct blade in the rotation plane

当浮式平台开始纵摇运动，平台运动的频率是0.1Hz，纵摇运动的周期是10s，在风轮旋转一周纵摇运动进行约半个周期，先向后运动到极限位置，再向前运动到平衡位置，如图7和图8中0°～360°方位角。在运动过程中，风电机组轮毂处的相对速度从低于11.4m/s 增加到额定风速，然后继续增加。在旋转平面0°～180°方位角，相对速度较低，不同展向位置Cn与Ct都较小，方位角180°～360°，相对速度增大，Cn与Ct增大。

当平台纵摇运动幅值较小时，相对速度变化较小，内叶展Cn与Ct先增加，随着相对速度的增加，中外叶展载荷逐渐增加。当幅值较大时，叶片旋转超过90°方位角，内叶展Ct率先增大，在叶片旋转超过180°方位角后中外叶展Ct开始逐渐增加。Cn在叶片旋转180°方位角附近开始增加，内叶展率先增加。平台纵摇运动使叶片在一个旋转周期内，表面受力发生周期性波动，而且随平台运动幅值增加，变化更剧烈。

风剪切来流条件下，Cn与Ct与叶片高度密切相关，从270°到90°方位角Cn先增大后减小，在0°方位角最大，叶片旋转到90°～270°方位角，风速降低导致Cn，Ct减小。随着剪切系数增加，来流风速在高度方向速度差增大，在风速较高的位置Cn增大，风速较低的位置Cn减小。外叶展Ct对来流风速非常敏感，风剪切系数0.2时，叶片旋转超过约15°方位角外叶展Ct开始减小。风剪切系数0.3 时，叶片旋转超过80°方位角，外叶展Ct开始减小。