基于LSTM-WPHM模型的风机轴承故障报警与寿命预测方法*

马明骏 赵海心 姜孝谟 成骁彬

(1.大连理工大学运载工程与力学学部 2.大连理工大学能源与动力学院，工业装备结构分析国家重点实验室，工业装备数字孪生辽宁省重点实验室)

0 引言

风电机组通常建造在如近海、草原和山区等偏远地带，受天气变化影响，其运行存在很大的随机性，且工况多变，加之自然环境极端恶劣，导致机组故障频发，运行成本居高不下[1]。对于在陆上偏远地区或海上的机组，维修时运输和吊装风机部件需要耗费较长时间，这使得机组停机时间长，维护成本高，降低了风机发电量和可靠性[2]，从而降低了风场的实际经济效益。因此，如何降低风电机组运营和维护成本是风电广泛应用和进一步发展的重大挑战[3]。剩余运行寿命预测可实现机组故障的早期预警和失效时间预估，帮助工作人员提前制定合理的维护计划，减少风机因故障导致的非正常停机，因而成为降低风电机组运维成本的有效手段。

轴承是传动链系统的关键部件之一，承担风机运行时的载荷传递。风机轴承在恶劣环境下运行，受变转速和变工况的影响，存在比其它工业轴承更高的故障率[4]。因此，对风机轴承开展寿命预测研究，实现轴承的故障预测，并制定出合理有效的维护策略，有助于降低风电机组的运维成本，提高风场的经济效益。

轴承寿命预测可分为基于物理机理和基于数据驱动的两类方法。前者根据失效机理建立相应的数学模型来描述轴承退化模式，并预测出剩余寿命，常用的方法包括基于裂纹扩展[5-6]和疲劳损伤[7-8]等机理模型。此类方法建模复杂，计算时间长，侧重于理论和试验研究，适用于轴承单一故障的寿命预测研究。后者基于海量历史数据，构建轴承寿命与关键变量之间的函数映射关系，实现对剩余寿命的预测，其预测精度依赖于数据和模型质量。此类方法通常可分为基于概率统计、机器学习和人工智能的三类方法。第一类方法根据大量轴承历史寿命数据，建立可靠性模型来预测轴承寿命，其中威布尔（Weibull）分布作为一种普适性的概率分布函数[9]，常应用于轴承的可靠性建模和分析[10]，来描述部件的不同失效模式。但该方法仅能反映轴承寿命的一般分布规律，对其在复杂运行工况下进行寿命预测时，会产生较大的偏差。第二和第三类方法都是根据轴承运行多变量监测数据，构建轴承寿命与多个关键变量的非线性关系来实现寿命预测。第二类方法通常基于比例风险、加速失效、逻辑回归和支持向量机等机器学习模型[11-14]来实现轴承寿命预测，这种方法在寿命预测领域发展相对比较成熟，适用性非常广泛。其中威布尔比例风险模型（Weibull Proportional Hazards Model，WPHM）[15]可对设备在不同状态下进行可靠性建模分析，被广泛应用于不同工业领域[16-18]。而第三类方法通常基于各种人工神经网络和深度学习模型[19-21]，此类方法在近几年迅速发展，其中长短期记忆（Long Short Term Memory，LSTM）神经网络，能考虑多维变量的相关性和时序前后依赖性，自动提取特征进行预测。本文发展一种融合WPHM 模型和LSTM 深度神经网络的混合方法，实现对风机轴承剩余寿命的准确预测。

目前，基于SCADA 数据的风电机组状态监测研究已取得不错的效果[22-23]，而基于SCADA数据的风机剩余寿命预测研究还处于初步阶段。在SCADA 数据中，温度能直观反映出轴承故障受复杂恶劣的运行环境和复杂工况影响，其表现不明显，给传统方法实现寿命预测带来困难。轴承温度通常与其它变量存在复杂的非线性关系，若根据健康状态下的数据，建立轴承温度与相关变量的映射关系，模拟出轴承温度在健康状态下的变化，便能识别出轴承的异常状态。

LSTM 神经网络作为循环神经网路（Recurrent Neural Network，RNN）的变体，在时序数据预测建模中表现出极强的适应性和很高的精度，同时解决了RNN的长期记忆能力不足、梯度消失和梯度爆炸等问题，因此在基于SCADA数据的风机状态监测方面取得了良好的效果[24-25]。但目前这些研究还没发展用于风电轴承剩余寿命预测。

本文针对风电轴承，发展基于SCADA 多维变量数据的无缝融合LSTM和WPHM的建模方法，实现轴承的故障预警和寿命预测有机结合。利用LSTM 预测模型集成风场环境和风机运行特性对轴承温度数据的影响，并根据预测得到的轴承运行状态指标，建立WPHM可靠性模型，实现对风机轴承的可靠性分析。根据分析结果，给出机组故障预警，同时对当前的可靠性变化趋势进行拟合，预测出机组未来的可靠性变化趋势，实现机组的剩余寿命预测。本文使用实际海上风场的发电机驱动端轴承运行数据和故障案例，验证所提出方法的有效性和准确性。

1 轴承剩余寿命预测模型

1.1 LSTM多变量预测模型

风电机组运行环境复杂，存在变转速、变工况等特性，导致轴承温度会出现周期性的波动，影响传统WPHM模型的可靠性分析精度。考虑到轴承温度与其它影响因素存在非线性关系，本研究建立LSTM多变量时序预测模型，拟合机组健康状态下轴承温度与相关变量的关系，由此预测轴承温度在健康状态下的理论值，并以实际值与预测值的残差作为轴承状态指标进行可靠性分析，实现更准确的剩余寿命预测。

根据风电领域的工程经验和专家知识，轴承温度主要与2 个方面的因素相关，一是与轴承自身转速相关，转速受运行工况影响，风速越大，功率越高，轴承转速就越快其温度也就高。二是与风机运行环境相关，轴承温度受昼夜交替、季节变化等外界环境的影响。对于发电机轴承，其温度还会受绕组温度的影响。发电机绕组和轴承位置相近，且绕组温度高于轴承温度，因此，发电机绕组的热量会传递给轴承，当绕组温度过高时，会导致轴承温度升高。

综上，本研究选取绕组温度、转速、风速、有功功率、环境温度和机舱温度6 个SCADA 系统变量作为模型输入，表示为X={x1,x2,…,x6} ，用于预测发电机轴承温度，表示为y。图1展示了LSTM-WPHM模型结构和算法流程，其中LSTM 轴承温度预测模型由2 层LSTM神经网络，2 层Dropout 层和1 层全连接层组成，每层LSTM后添加的Dropout层，在每次迭代训练中随机减掉20%的神经元，以减少模型出现过拟合的概率。

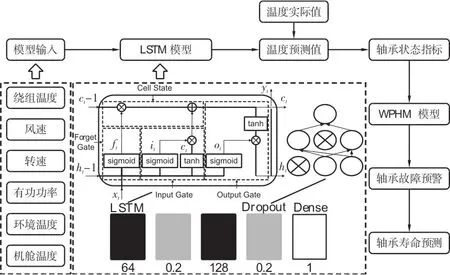
图1 LSTM-WPHM模型结构和应用流程Fig.1 Architecture and application process of LSTMWPHM

LSTM 神经网络是一种递归神经网络，其通过引入输入门、遗忘门和输出门来实现删除或增加信息到细胞状态，对处理长时间序列数据问题上更具优势[30]。模型中Ct为细胞状态单元，表征长期记忆，ht为隐层状态单元，表征短期记忆，ft，it和Ot分别为遗忘门控单元、输入门控单元和输出门控单元，代入某个时刻的SCADA变量Xt，ft，it和Ot可表示为：

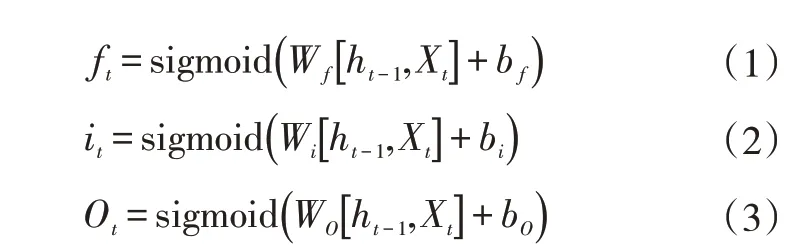
式中，Wf，Wi和WO为各门控单元的权值矩阵，bf，bi和bO为各门控单元的偏置矩阵。模型中遗忘门是将长期记忆中的不相关信息进行遗忘，保留重要信息，其中遗忘门控单元ft用于调节长期记忆Ct的遗忘程度。输入门是对短期记忆中的信息进行更新，并从中筛选出重要信息作为候选记忆单元添加进长期记忆，其中输入门控单元it用于调节候选记忆单元的添加程度，可表示为：

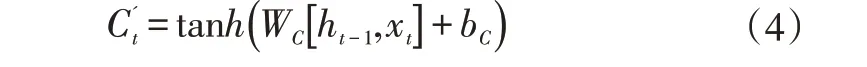
式中，WC为候选记忆单元的权值矩阵，bC为候选记忆单元的偏置矩阵。输出门是对遗忘门和输入门的信息进行汇总，更新细胞状态单元Ct和隐层状态单元ht，并给出模型输出yt，表达式如下

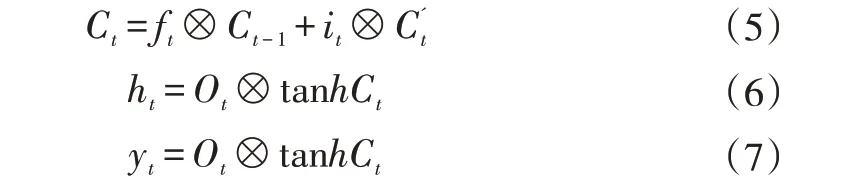
式中，符号⊗表示矩阵乘法运算；ft⊗Ct-1表示记忆遗忘阶段；it⊗表示记忆更新阶段。选取风机轴承健康阶段的运行数据，训练LSTM轴承温度预测模型，建立轴承温度与6个影响因素的映射关系。利用LSTM模型预测出轴承正常运行的温度值，当轴承发生异常时，预测值与实际值会发生较大偏差。因此，本文以预测值与实际值的残差δ作为表征轴承状态的指标，计算公式如下：

式中，ytrue和ypre分别为轴承温度实际值和预测值。

1.2 WPHM轴承可靠性模型

传统的比例风险模型（Proportional Hazards Model，PHM），又称Cox 模型，是由英国统计学家D.R.Cox 提出的一种半参数统计回归模型。该模型假设设备在t时刻的失效率λ(t,X)由两个影响函数组成，即基线失效率λ0(t)和监测变量X影响的指数函数g(X)。本研究将式（8）得到的轴承状态指标δ代入模型，得到LSTMPHM的失效率表达为：

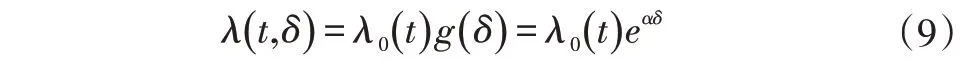
式中，λ0(t)为仅与历史寿命t有关的基线失效率函数，g(δ)=eαδ为影响轴承故障的关键变量函数，α为对应的回归系数，反映状态指标对机械设备失效的影响程度。相较于传统PHM 模型，本研究提出的模型通过LSTM 模型融合6 个关键变量X={x1,x2,…,x6} 为轴承状态指标δ，不仅有效地集成了多个关键变量的影响，而且极大地简化了PHM模型参数的估计。

传统的PHM模型不假定λ0()t的分布形式，仅根据现有数据给出离散型的基线失效率，无法给出随历史寿命变化的连续型基线失效率。考虑到不同机械设备在特定工况下都有其相应的失效分布函数，本研究将可靠性函数中常用的Weibull分布引入式（9），建立全参数统计回归的LSTM-WPHM 模型，来对机械设备进行更准确地分析，其失效率函数表达式为：

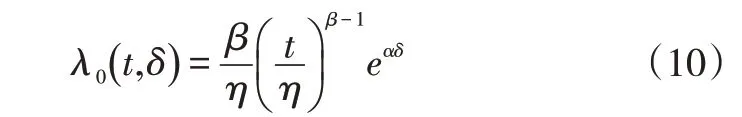
式中，η和β分别为Weibull分布的尺度参数和形状参数，其中β＜1表示故障发生在早期阶段，通常由材料或制造等因素导致；β＞1表示故障发生在老化阶段，由设备长时间运行引起的磨损、疲劳和腐蚀等因素导致；β=1表示在运行过程中故障发生是随机的。

LSTM-WPHM 轴承可靠性模型中的未知参数采用极大似然法进行估计，其对数似然函数为如下：

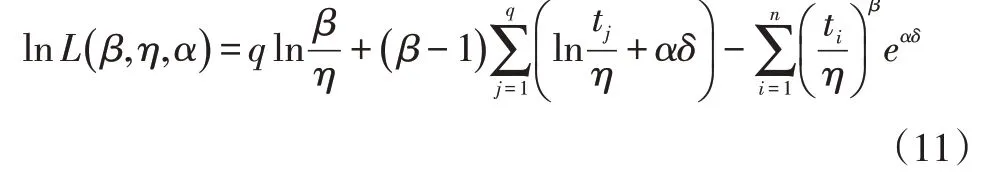
式中，q为样本失效个数；n为数据样本总数。对lnL(β,η,α)中的未知参数β，η和α分别求偏导，并令各偏导数等于零得到非线性方程组，利用BFGS 迭代算法求解该方程组，得到参数估计值，和。

根据可靠性原理，LSTM-WPHM模型的累积失效概率为：

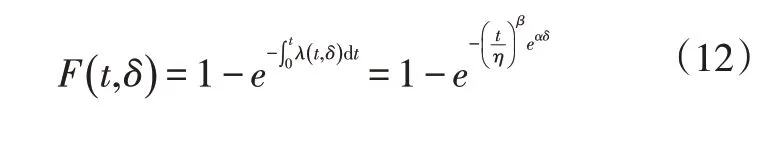
根据式（12）对给定机组进行可靠性分析，计算风机轴承随运行时间变化的累积失效概率F(t,δ)。累积失效概率能够表征轴承的故障程度，其数值越大，说明轴承损伤的程度越大。因此，以累积失效概率作为轴承的失效指标，并根据故障机组和健康机组的分析结果，确定出机组的报警阈值Fa和失效阈值Ff，用于机组的故障报警和寿命预测。

1.3 LSTM-WPHM模型故障报警及寿命预测

图2 为LSTM-WPHM 混合模型对机组故障报警和寿命预测的示意图。首先通过LSTM 模型融合多维变量数据，计算出轴承状态指标，然后根据式（12）计算出轴承的累积失效概率F，当F达到报警阈值Fa时，给出机组故障预警，并开始对机组进行寿命预测分析。本研究对F变化趋势进行曲线拟合，预测机组F未来的变化趋势，当预测的F值达到失效阈值Ff时，判定轴承完全失效。轴承运行出现报警时，通常认为其出现了早期故障征兆，在没有维修的情况下，轴承失效概率会随着运行时长呈现非线性单调上升趋势。因此，本研究采用指数函数来拟合失效概率趋势，表达式为：

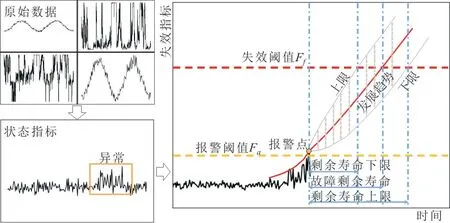
图2 故障报警与剩余寿命预测相结合的示意图Fig.2 Schematic diagram of fault alarming and remaining life estimation simultaneously

式中，t为机组轴承运行时长。当达到失效阈值Ff时，轴承的剩余寿命tRUL为

式中，ta是机组报警时间；tpf是预测出的轴承失效时间。

风电机组运行存在很大的随机性，这导致风机轴承实际运行寿命也存在较大的不确定性。本研究通过拟合曲线参数估计的置信区间，给出失效指标趋势变化的上下限，从而得到机组轴承的剩余寿命区间，进而定量化剩余寿命的不确定性。由此，通过LSTMWPHM 混合模型，同时实现对风机轴承运行故障报警和剩余寿命预测的有机结合。

2 算法流程

本文所提出的轴承故障报警和寿命预测相结合的算法流程如图3所示，具体步骤如下：

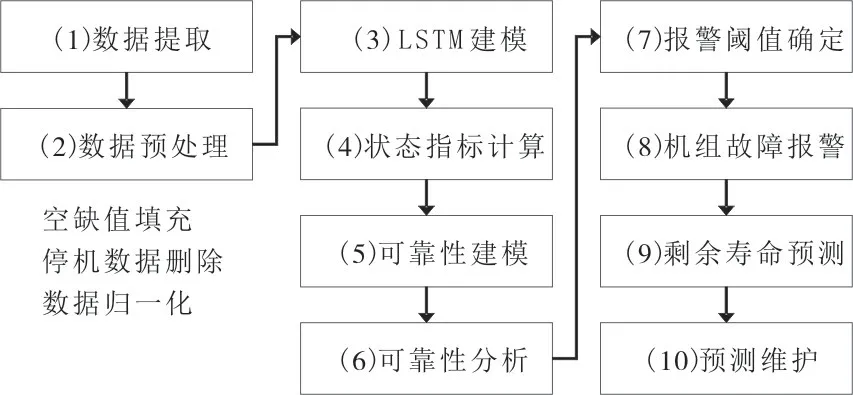
图3 故障报警及寿命预测算法流程Fig.3 Algorithm flow of fault alarm and life prediction

1）数据提取：从机组SCADA系统中提取建模所需的7个相关变量数据作为机组原始数据。

2）数据预处理：对数据中的空缺值和停机数据进行处理，其中对空缺值采用中位数进行填充，对有功功率小于0 或风速小于3m/s 的风机停机数据进行删除。对不同变量数据进行归一化处理，使数据映射到0～1之间，以消除变量间的量纲影响。

3）LSTM建模：利用前面所述的LSTM建模方法构建健康状态下各关键变量与轴承温度的非线性映射关系。

4）状态指标计算：以LSTM模型给出的轴承温度预测值和实际值的残差作为表征轴承运行状态的指标，以此融合各类因素对轴承温度的影响。

5）可靠性建模：选取故障机组在故障发生时刻和健康机组在多个不同时刻下的变量数据作为建模数据，根据式（10）建立LSTM-WPHM 混合可靠性模型，并利用极大似然估计方法估计模型参数。

6）可靠性分析：基于LSTM-WPHM模型，根据等式（11）对机组进行可靠性分析，给出机组随时间变化的累积失效概率。

7）报警阈值确定：通过分析训练集中故障机组和健康机组的累积失效概率差异，确定报警阈值Fa和失效阈值Ff。

8）机组故障报警：基于LSTM-WPHM 模型对机组的分析结果，根据报警阈值和故障阈值，实现机组的实时监测和多级故障报警。

9）剩余寿命预测：当模型给出机组故障预警时，根据机组的可靠性分析结果，利用式（13）拟合机组的累积失效概率变化趋势。基于拟合曲线预测机组该指标的未来变化，并根据式（14）计算出机组故障剩余寿命区间，从而实现机组故障报警和寿命预测的有机结合。

10）预测维护：基于LSTM-WPHM得到的故障报警和预测的剩余寿命，提前规划轴承维修范围和策略，准备维修资源和备件，实现基于设备运行条件的预测性维护。这样减少轴承因故障导致的非计划停机，提高风机轴承的可靠性，减少维修停机时间，降低维修成本。

3 算例验证

3.1 算例数据

以某海上风场4MW风电机组中的发电机驱动端轴承故障为例，利用24 台故障机组和75 台健康机组从2016年到2019年的SCADA数据作为训练集，24台故障机组和20 台健康机组2020 年的SCADA 数据作为测试集，对模型和方法进行验证。首先从SCADA 系统中提取驱动端轴承温度、绕组温度、转速、风速、有功功率、环境温度和机舱温度7 个变量的数据，并根据上述流程，对变量数据进行预处理，包括填充空缺值、删除停机数据和数据归一化。同时，对采样间隔为10 分钟的原始SCADA 数据进行降频，通过计算每1 小时内的数据均值，得到采样间隔为1小时的降频数据。

3.2 LSTM温度预测模型

受变转速、变工况以及环境变化的影响，轴承温度会呈现周期性的波动。图4 展示了3 个相关温度变量的变化趋势，可以看出驱动端轴承温度变化趋势与绕组温度和环境温度的趋势相同，说明驱动端轴承温度会受到绕组温度和环境温度的影响。

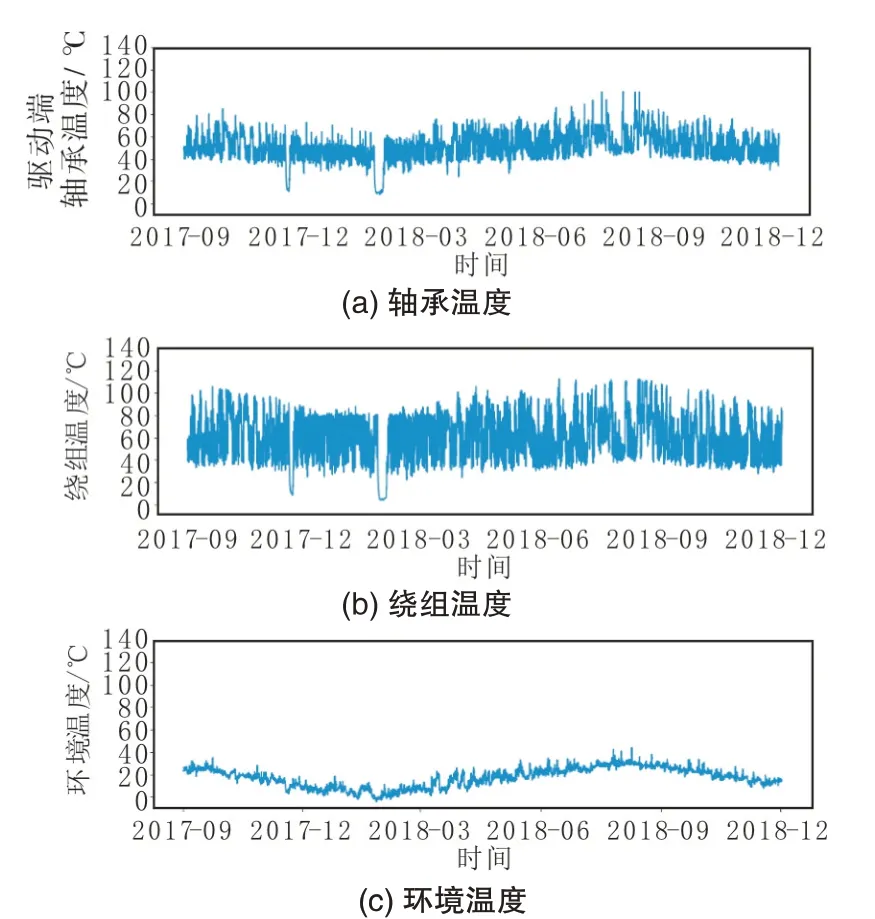
图4 温度变量变化趋势Fig.4 Temperature variable trends

选取预处理后的每台机组至少6 个月的健康运行数据作为训练集，建立LSTM 轴承温度预测模型，构建健康状态下各影响因素与驱动端轴承温度的映射关系。图5为训练集中部分机组的模型训练过程，可以看出，随着迭代次数的增加，训练误差和验证误差均逐渐趋于平稳，说明LSTM模型已经收敛。

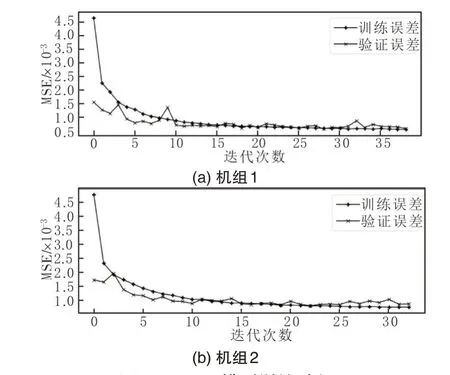
图5 LSTM模型训练过程Fig.5 Training error of LSTM model

利用非训练集的健康运行数据对LSTM 模型进行验证，图6 为训练集中99 台机组的模型决定系数（RSquare，R2）和均方误差（Mean Squared Error，MSE）分析结果，可以看出，训练集中97%机组的R2大于0.8，R2的平均值为0.881，91.9%机组的MSE小于0.001，MSE的平均值为0.00067，说明LSTM模型的拟合精度非常高。

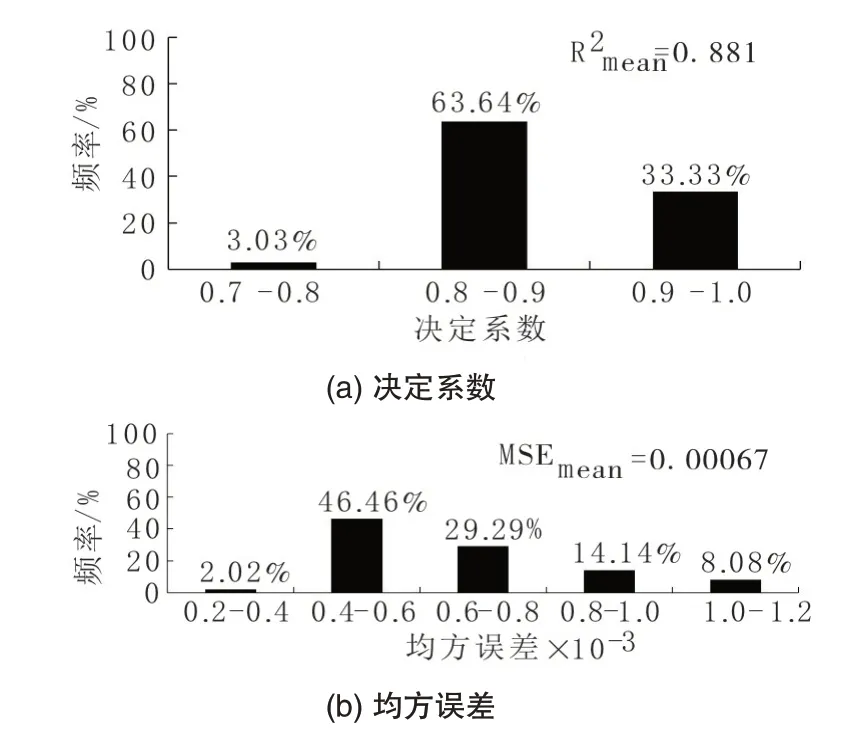
图6 LSTM模型验证结果Fig.6 Validation results of LSTM model

利用LSTM 模型计算出健康状态下的驱动端轴承温度预测值，并以预测值与实际值的残差作为表征驱动端轴承运行状态的新指标，来消除驱动端轴承温度的波动性，进而突显出驱动端轴承温度异常。图7展示了驱动端轴承原始温度和LSTM 模型计算出的轴承状态指标数据，可以看出，新的轴承状态指标相比于原始轴承温度更为平稳，且能够更明显地反映出机组运行过程中的轴承异常。

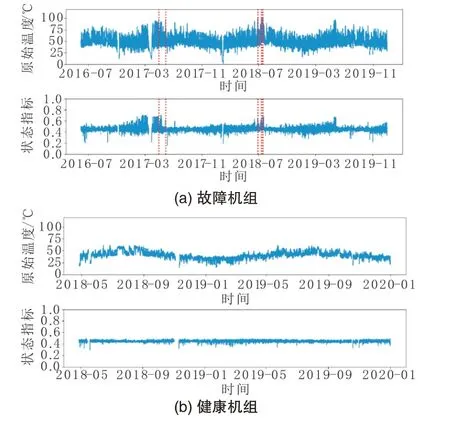
图7 驱动端轴承原始温度和状态指标Fig.7 Drive-end bearing original temperature and condition indicator

3.3 模型比较

选取训练集中的24台故障机组在故障时刻和75台健康机组在多个任意时刻下的变量数据，分别建立发电机驱动端轴承故障的WPHM模型和LSTM-WPHM模型。表1 为两种模型的参数估计结果，可以看出，两种模型的参数β均大于1，α均大于0，说明两种模型均模拟该故障为退化失效模式，且驱动端轴承温度越高，故障程度越大，符合轴承故障机理。两种模型的p值均为0，说明建立的两种模型均有较高的拟合精度。

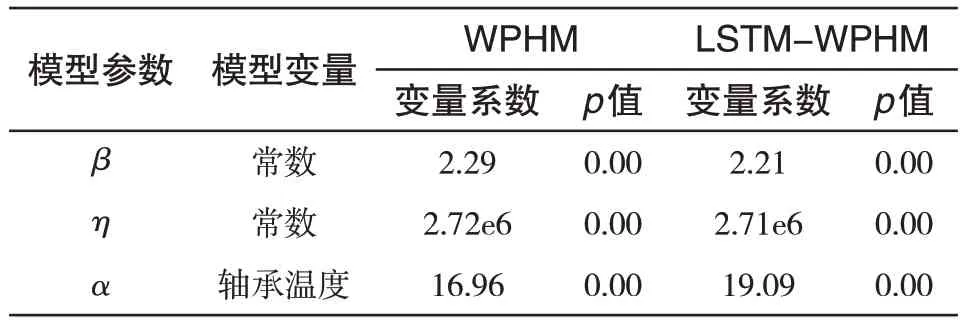
表1 模型参数估计结果Tab.1 Parameter estimation results of models

利用得到的WPHM和LSTM-WPHM模型分别对故障机组A和健康机组B进行分析。图8和图9分别展示了两种模型对故障机组A和健康机组B的分析结果，红色垂直虚线为SCADA系统故障报警时刻，可以看出，两种模型均能识别出轴承故障，且能捕捉到轴承的失效退化阶段，实现机组故障预警，但LSTM-WPHM 模型对机组健康阶段计算出的累积失效概率更低，更符合轴承的健康运行状态，特别是对于健康机组，可以明显地减少对机组的误报。

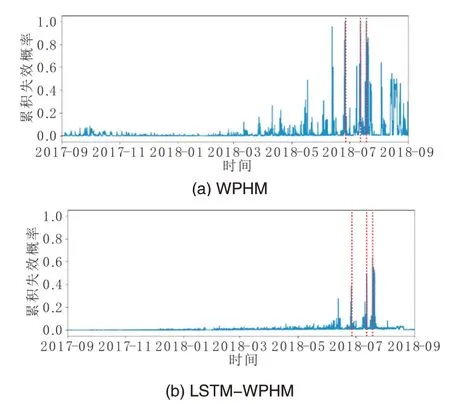
图8 故障机组A累积失效概率分析结果Fig.8 Cumulative failure probability analysis of faulty unit A

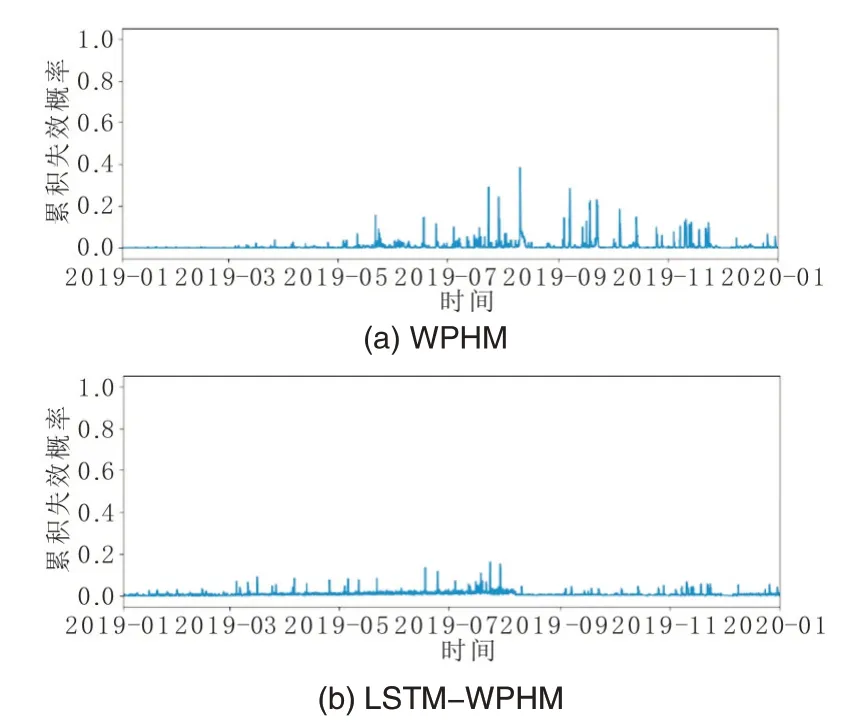
图9 健康机组B累积失效概率分析结果Fig.9 Cumulative failure probability analysis of healthy unit B

3.4 故障报警与寿命预测

根据式（12）对训练集中的24台故障机组和75台健康机组进行分析，通过对比故障机组和健康机组的分析结果，确定驱动端轴承故障的报警阈值和故障阈值。图10为训练集机组累积失效概率分析结果的统计特征散点图，可以看出，80%故障机组的累积失效概率最大值大于0.5（红色虚线），而所有健康机组的最大值小于0.2（黄色点划线）。因此本研究分别选取0.2和0.5作为报警阈值Fa和故障阈值Ff，实现轴承故障的多级报警。从图10 中还可以看出，全部机组的累积失效概率均值均小于0.05（蓝色点线），而大部分健康机组的累积失效概率最大值大于0.05（蓝色点线），表明部分健康机组可能已经存在故障的风险，所以本研究选取0.05作为识别轴承可靠性出现异常的阈值，开始捕捉轴承异常变化趋势，实现轴承故障预测。

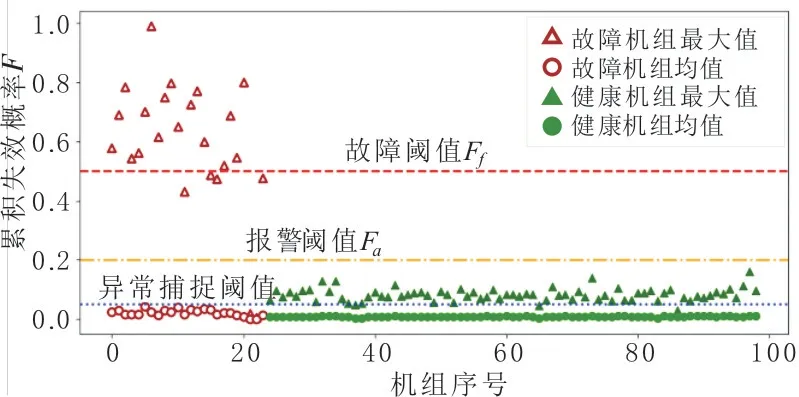
图10 机组累积失效概率分析结果的统计特征Fig.10 Statistical characteristics of cumulative failure probability analysis results for all units

当累积失效概率超过0.2 时，轴承进入失效退化阶段，给出轴承故障预警，并根据报警前6 个月的数据对轴承进行寿命预测分析。基于识别到的轴承异常数据，利用式（13）拟合机组累积失效概率随运行时间的变化趋势，预测轴承未来的累积失效概率，利用式（14）估计出轴承的剩余寿命。考虑到运行过程中机组寿命存在较大的不确定性，本文基于拟合曲线参数估计的99.5%置信区间，给出累积失效概率变化趋势曲线的上下限，从而给出机组剩余寿命的预测区间。

利用2 台故障机组C 和D 对提出的故障报警及寿命预测方法进行验证，图11 展示了LSTM-WPHM 模型对2 台故障机组的故障预警和寿命预测分析结果。故障机组C在2019/06/02 16:11发生故障，模型在2019/04/05 22:00 给出机组故障预警，并预测机组在606 小时到1562小时之间发生故障，提前了57天18小时预测出机组故障（图11a）。故障机组D 在2020/06/02 07:53 发生故障，模型在2020/04/30 22:00给出故障预警，并预测机组在599 小时到963 小时之间发生故障，提前32 天9 小时预测出机组故障（图11b）。由此说明，本文提出的故障报警和寿命预测相结合算法能够提前给出预警，并可以准确地预测出机组发生故障前的剩余寿命。

图11 LSTM-WPHM模型故障报警与寿命预测分析结果Fig.11 Analysis results of LSTM-WPHM fault alarm and life prediction

3.5 算法精度验证

为进一步验证所提方法的准确性和有效性，利用上述方法对测试集中的24台故障机组和20台健康机组进行故障报警和寿命预测分析。表2 为测试集机组报警结果，可以看出，对24 台故障机组给出19 次故障报警，其中3 次为机组健康阶段的误报，报警准确率为66.7%，对20 台健康机组给出7 次误报，报警准确率为65%。可见，机组报警整体准确率为65.9%，准确率较低，且测试集机组报警中的误报率也相对较高，整体误报率为25.6%。

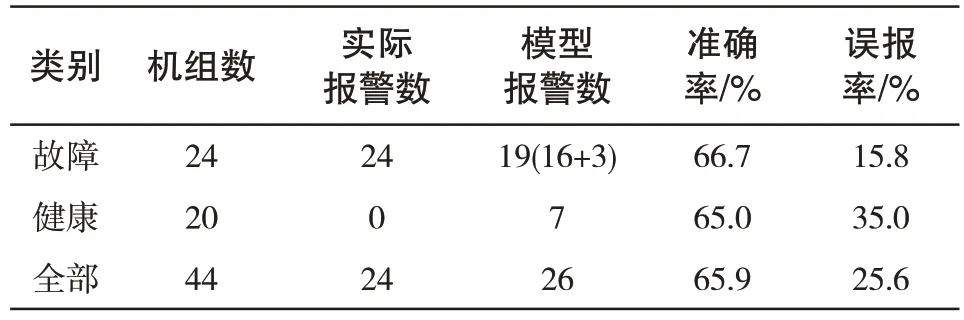
表2 测试集机组报警结果Tab.2 Alarm analysis results of test units

针对上述误报和漏报情况，选取典型机组进行分析。图12 为测试集中误报机组的两个分析案例，对于故障机组E，模型在2020 年3 月给出故障报警，而系统并未发生报警，但从原始轴承温度可以看出，温度存在异常，但由于没有达到系统设置的90℃的报警阈值，所以系统没有给出警报，因此考虑该误报为模型识别出的系统漏报。同理，对于健康机组F，模型在2020年10月至11 月给出故障报警，但由于原始轴承温度并未达到系统报警阈值，所以没有给出警报。

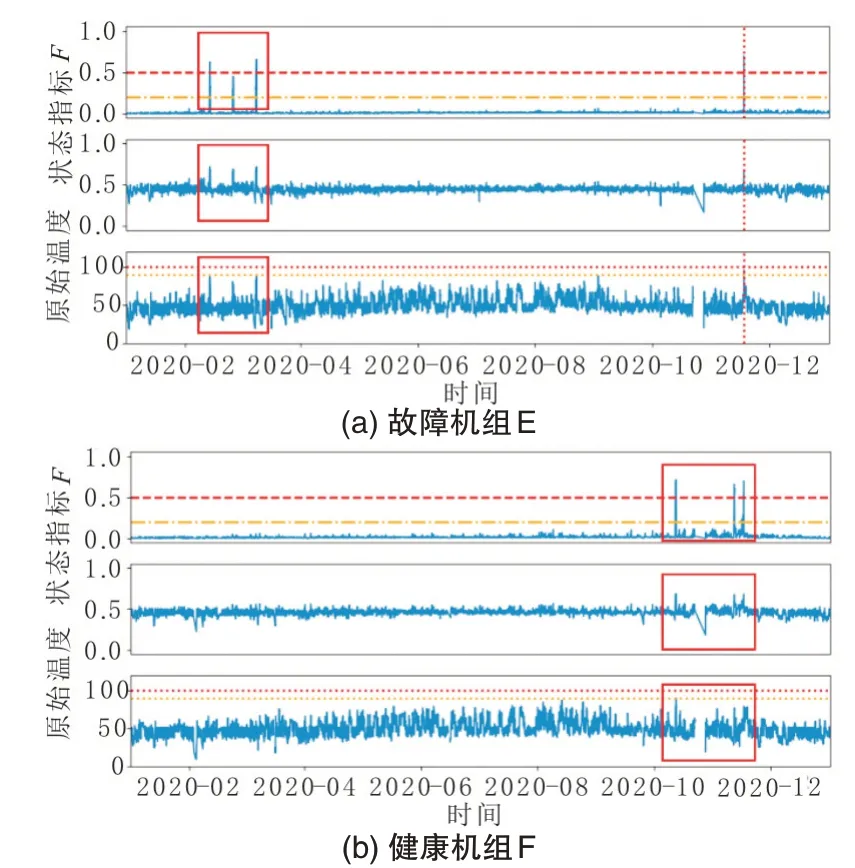
图12 误报机组的分析结果Fig.12 Analysis results of false alarms

测试集中的机组误报大多为系统未识别出的漏报，若考虑上述情况，测试集的10次误报中有8个为系统漏报，其中3 个为故障机组，5 个为健康机组，由此重新计算测试集的机组报警结果，如表3 所示，机组报警整体准确率为78.7%，误报率为4.3%，故障预测平均提前时间为13天7小时。

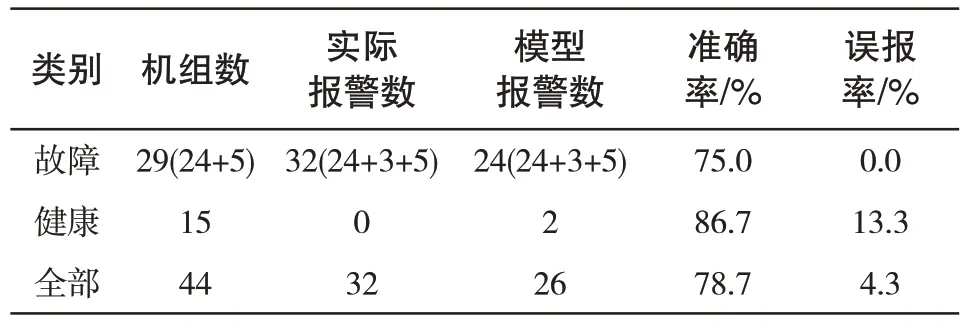
表3 测试集机组报警结果Tab.3 Alarm analysis results of test units

图13为测试集中漏报机组的2个分析案例，可以看出，模型未在机组故障时刻给出报警，从原始轴承温度可以看出，温度确定超过了系统报警预警，但经模型分析后，轴承状态指标在故障发生时刻未有明显变化，原因可能是轴承温度超限主要受其它因素影响，并不是模型考虑的影响因素或机组自身故障所致。

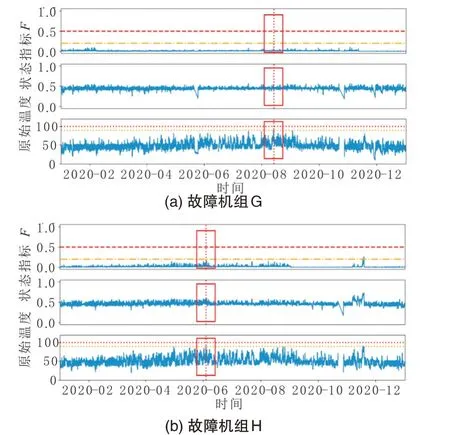
图13 漏报机组的分析结果Fig.13 Analysis results of missing alarms

综上，本文所提出的方法能够高精度地实现机组的故障报警和寿命预测，同时模型能够识别出受环境因素影响而导致的系统漏报，说明本文提出的模型和方法具有很高的准确性。

4 结论

针对风机轴承温度异常监测报警和预测，本文提出一种基于SCADA数据的LSTM-WPHM混合模型。通过引入LSTM 模型，融合关键因素对轴承温度的影响，提高轴承温度异常的识别精度，并结合给出的轴承状态指标，发展LSTM-WPHM 模型，提出一种风机轴承故障报警和寿命预测相结合算法，提高风机轴承异常报警、可靠性分析和剩余寿命预测的精度。考虑风机轴承因多种因素影响导致的运行寿命的不确定性，给出剩余寿命预测区间，以便制定合理的维修计划。利用实际海上风场SCADA 系统的发电机驱动端轴承数据，通过比较研究，验证了本文所提模型和方法的有效性和准确性，具体结果如下：

1）以1台故障机组和1台健康机组为例，对LSTMWPHM 模型和传统WPHM 模型进行对比分析，结果表明，LSTM-WPHM模型可以更准确地得到机组可靠性分析结果，并减少机组误报情况。

2）以测试集中的2台故障机组为例，对所提出的方法进行验证，结果表明，该方法能够基于LSTM-WPHM模型分析结果，根据报警阈值和故障阈值，准确地实现机组故障报警，并根据指标变化趋势，准确预测出故障发生时间，实现故障报警和寿命预测有机结合。

3）利用测试集中的全部机组对所提出的基于LSTM-WPHM 的方法进行验证，结果表明，该方法能够以较高精度实现故障报警和寿命预测，故障报警整体准确率为78.7%，并可以平均提前13天7小时给出故障预测，从而验证了本文所提方法的准确性和有效性。