大方捆打捆机压缩室轻量化研究

闫振洋 杜冲冲

1.石家庄邮电职业技术学院 河北石家庄 050022；2.三一重工股份有限公司 湖南长沙 410100

我国是农业大国，秸秆和牧草资源丰富，打捆后再利用可以提高资源利用率[1]。牧草秸秆打捆机是实现农业机械化与农业生物资源利用的主要设备之一，大方捆打捆机由于其工作效率高，需求量逐年增加。高雄等对大方草捆压捆机喂入机构进行运动分析与优化，增加了喂入量[2]。郭辉等设计了一种基于工作负荷反馈的轮式自走方捆打捆机，降低了打捆机行走的动静偏差与调整时间[3]。王国权等对秸秆捡拾打捆机的捡拾器进行动力学仿真研究，提高了捡拾效率[4]。陈锋对大方捆打捆机进行压缩机构设计及压缩试验研究，获得合适的参数与结构[5]。

然而对大方捆打捆机压缩室的设计研究较少，主要参考国外尺寸与壁厚，或者根据经验进行设计加工。对大方捆压缩室进行参数化建模，采用基于拉格朗日的非线性规格优化算法进行压缩室轻量化。

1 参数化模型

Creo具有Pro/Engineer的参数化技术、CoCreate的直接建模技术和ProductView的三维可视化技术三者的优势，利用Creo建立900mm×1200mm×2000mm大方捆打捆机压缩室结构参数化模型，如图1所示。共计8个参数，其中加强筋厚度为DS_D1；加强筋宽度为DS_D；第一加强筋距离压缩室的端口的距离为DS_L1；第三加强筋距离压缩室的出口的距离为DS_L2；第二加强筋与第一加强筋的距离为DS_L3；第四加强筋距离出口的距离为DS_L5；第五加强筋距离出口的距离为DS_L4。

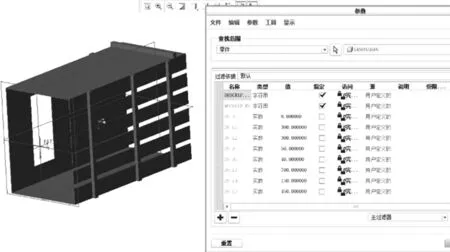
图1 压缩室参数化模型

8个参数优化过程非常消耗计算资源，在参数优化之前进行参数关联性分析很有必要，可以获得参数与输出之间的敏感度，识别主要参数，剔除不重要的参数，从而简化计算，节约计算成本。建立Creo与ANSYS之间数据交换接口，将有限元分析结果中的质量、最大应力以及最大变形作为输出。压缩室输入参数和输出参数敏感度如图2所示。

图2 参数敏感度

DS_H厚度对质量和变形敏感度最大，DS_D1对应力敏感度最高。关联性阀值为0.5，即小于0.5的为次要参数，大于0.5为主要参数。在八个结构参数的计算中，DS_H，DS_D，DS_D1，DS_L1，DS_L2为主要参数，DS_L3，DS_L4，DS_L5为次要参数，如图3所示。

图3 参数关联度分析

2 Kriging代理模型

代理模型是指在进行优化设计的时候可以“代替”那些计算复杂且费时的数值分析或者有限元模型的数学模型，又被称为“近似模型”“响应面模型”或“元模型”[6-7]。设原函数为y(x)，Kriging模型可以表示为：

yi(x)=f(x)Tβi+zi(x)i=1，2，…，q

(1)

式中：f(x)T为已知的回归模型，一般为多项式函数，βi为回归系数，zi(x)为随机过程函数，它的均值为0，方差为σ2，协方差矩阵为：

cov[z(xi)，z(vi)]=σ2R(xi，vi)

(2)

其中，R(xi，vi)为两个数据点x、v之间的变异函数，可采用高斯函数类型，表达式如下：

(3)

式中：n为维数，θ为相关性参数。

由实验数据样点值和它们对应的计算值，组成一个相关矩阵：

(4)

式中：m为样本点个数。

设x0为预测点，其与样本数据点之间的相关矩阵为：

(5)

由样本点组成的相关矩阵为：

(6)

根据样本点，利用拉格朗日乘子法与极大似然估计可以获得相关性参数θ、β和σ2的估计值：

(8)

联立上述方程可以获得预测点x0的估计值为：

(9)

为了建立Kriging近似模型，需要一定数量的样本数据，拉丁超立方抽样法具有优异的整体空间均布填充能力，可以保证在多参数区间内获得较好的实验样本点[8]。拉丁超立方体抽样的基本步骤是：

(1)将每一维分成互不重叠的m个区间，使得每个区间具有相同的概率。

(2)在每一维里的每一个区间中随机的抽取一个点；

(3)然后从每一维里随机抽出的步骤(2)中选取的点将它们组成向量。

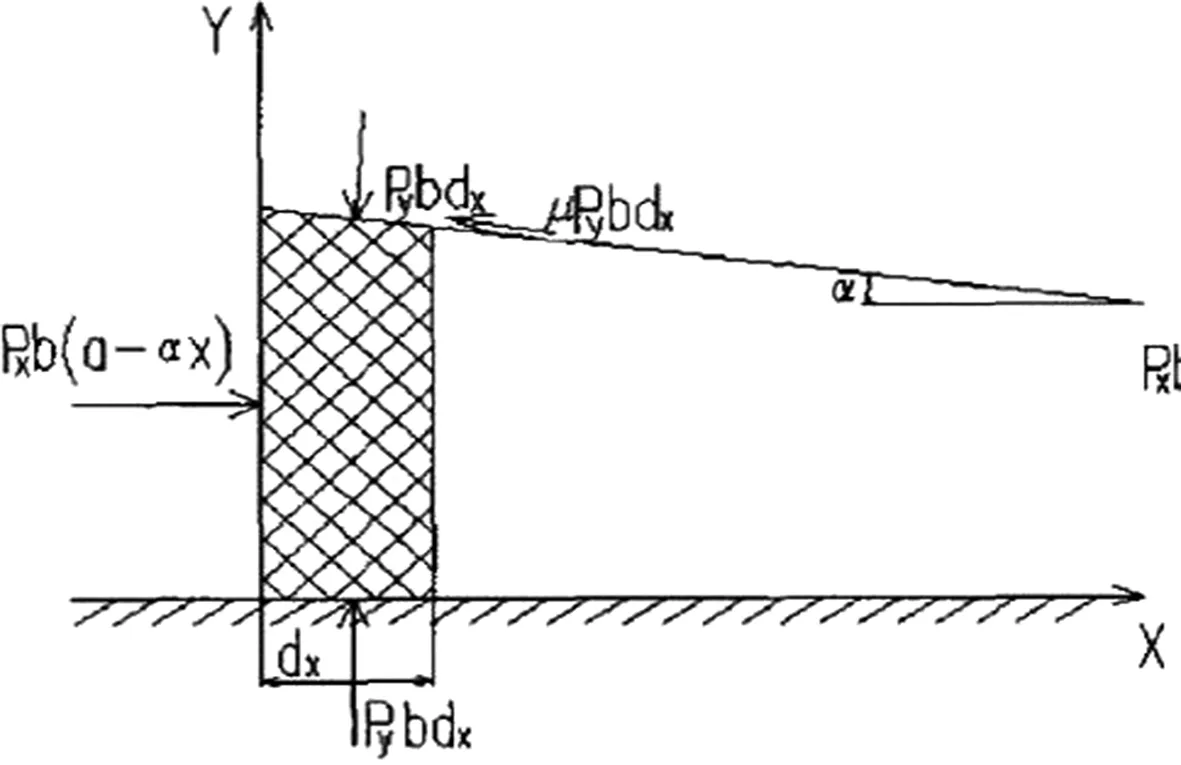
A侧视图图4 压缩室截面图

从压缩室的入口到出口存在一定的坡度如图4所示，利用坡度与压缩活塞对牧草等原料进行压缩，根据压缩理论[5]，压缩室壁面力与活塞力平衡公式如下：

(10)

在ANSYS软件workbench操作平台中，将压缩室入口和地面设置为固定约束条件，其余壁面以压力函数作为负载，材料选为Q235，输入参数为5个主要参数，输出为最大应力和质量，获取超拉丁立方样本点数据如图5所示。

图5 拉丁超立方样本点

根据拉丁超立方抽样的样本点建立Kriging代理模型，设置验证点并采用响应点和验证点的数值进行对比。相同参数下Kriging代理模型响应点最大应力为197.5MPa，验证点最大应力为200MPa，误差为1.26%，质量误差为0.02%，误差在允许范围内。

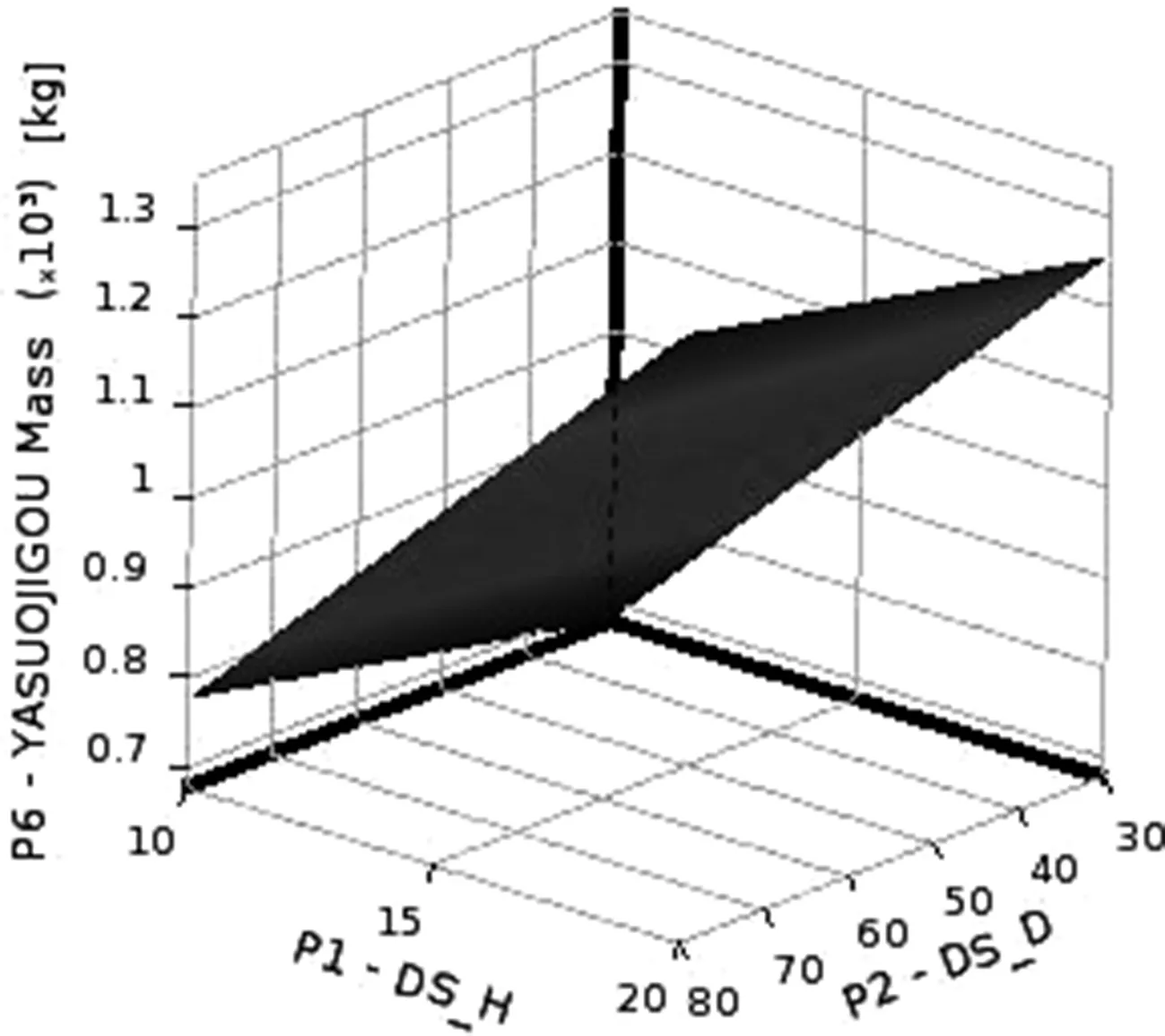
图6 参数DS_H，DS_D与输出质量响应

图6为压缩室输入参数DS_H，DS_D与输出质量响应面，输出压缩室质量随着DS_H，DS_D增加而增加。图7为输入参数DS_D，DS_D1与输出最大应力响应面，从图中可以看出当为输入参数DS_D，DS_D1都减小时，最大应力显著上升，响应面为陡峭曲面。

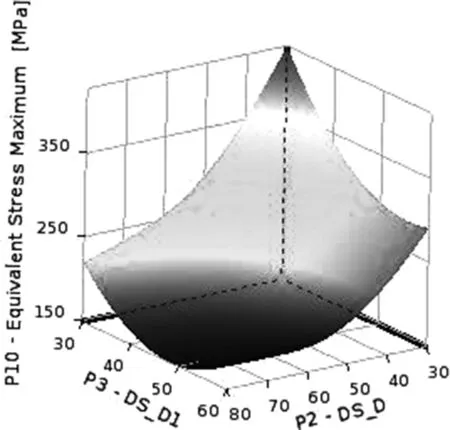
图7 输入参数DS_D，DS_D1与输出最大应力响应面

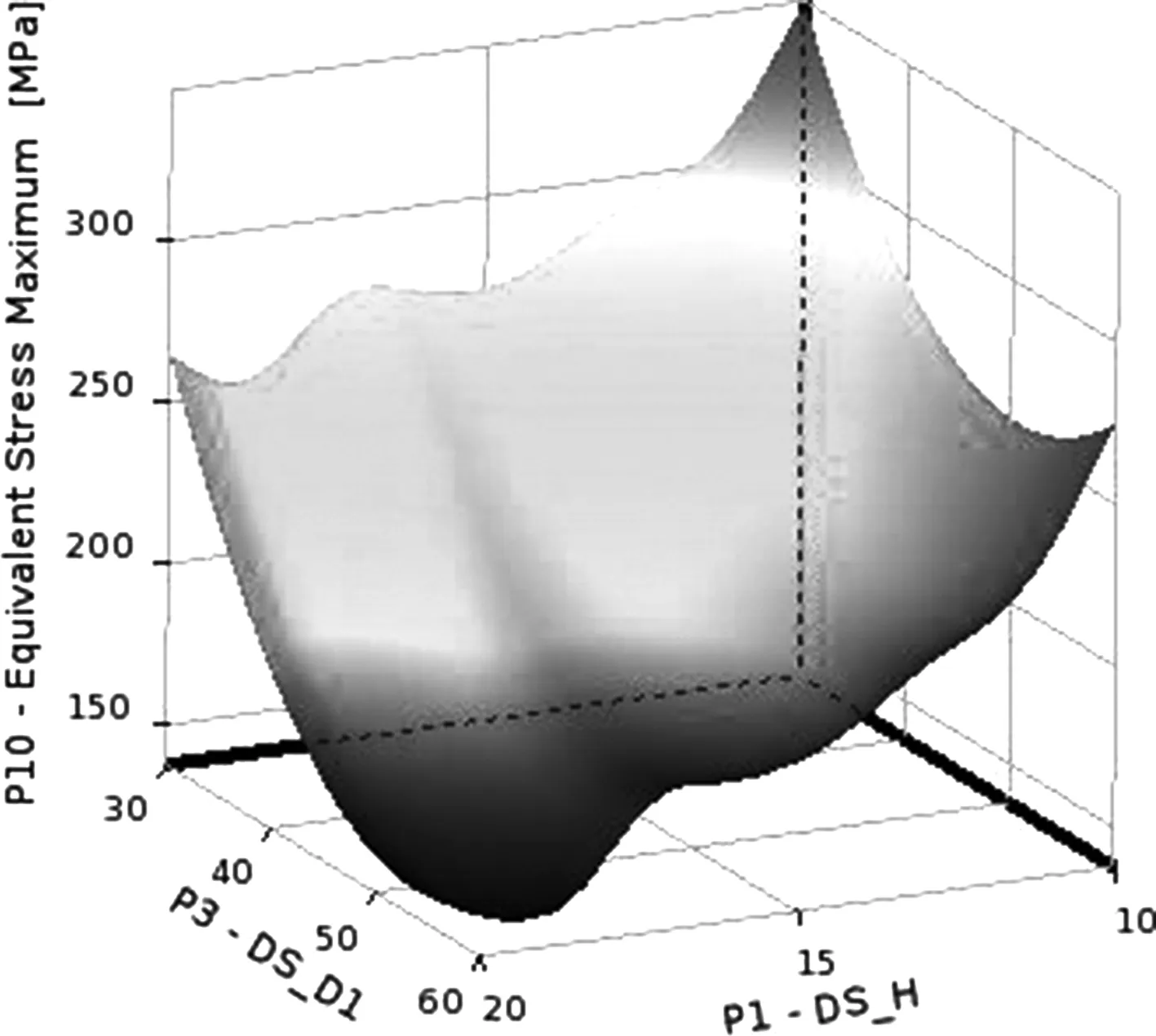
图8 参数DS_H，DS_D与输出最大应力响应面图

图8为参数DS_H，DS_D与输出最大应力响应面，最大应力随着输入参数增大而迅速下降，并且存在显著凹凸部位，在一个参数增大，而另外一个参数减小的时候，最大应力出现不同的变化，在变量区间内输入参数对输出最大应力贡献度不同。

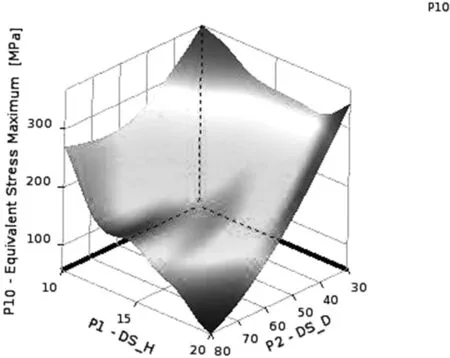
图9 输入参数DS_H，DS_D1与输出最大应力响应面

图9为DS_H，DS_D1与最大应力响应面，从图中可知，输入参数DS_H和DS_D1对最大应力的作用更为复杂，存在多个显著凹凸部位，当一个输入参数增加而另外一个参数固定时，最大应力出现非线性变化，先减小后增加。

3 拉格朗日非线性规划算法与优化

在ANSYS软件workbench操作平台中提供了基于拉格朗日的非线性规划优化算法，是一种基于梯度的单目标优化方法，其基础为准牛顿法，可以通过设置允许的收敛残差来提高计算准确度。设定压缩室整体质量m为优化目标，最大应力为优化的约束条件，多参数优化数学模型如下：

(11)

设定允许残差为10-6，迭代步数为150步，约束条件和质量目标函数如图10和图11所示，在迭代接近40次时候，约束与目标函数均收敛，将最优点重新作为验证点，验证计算结果如下表。

验证结果表

上表中第三行为圆整后的优化参数，第四行为初始参数，质量目标下降20.3%，而最大应力下降12.5%，优化效果显著，并且满足许用应力条件。图12和图13为压缩室轻量化前后应力分布云图。

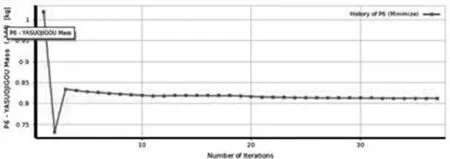
图10 约束变化曲线

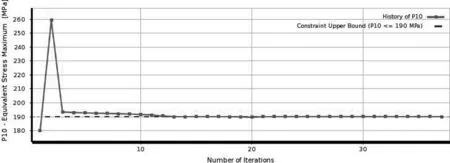
图11 质量目标函数变化曲线

图12 初始参数仿真云图

图13 轻量化后仿真云图

结论

针对打捆机压缩室依靠经验设计、耗材量大等问题：

(1)建立8参数模型，以压缩室质量为优化目标，以最大应力为优化约束条件，进行参数关联性与敏感度分析，排除不重要参数，获得DS_H，DS_D，DS_D1，DS_L1，DS_L2五个主要参数；

(2)通过拉丁超立方抽样，获得优异样本点建立Kriging代理模型，并通过验证点验证模型误差为1.26%，获得压缩室参数输入与目标输出的响应曲面；

(3)利用基于拉格朗日的非线性规划优化算法，通过圆整输入参数获得最优质量目标，与初始参数相比，质量减轻20%。