基于扩展Jarvis-Patrick聚类的异常检测算法优化及检测仿真
2022-07-08张利剑陈晋鹏
张利剑,陈晋鹏
(西安工程大学电子信息学院,陕西西安 710048)
异常检测方法主要对已知数据的整体进行建模分析,从中识别和记录异常数据。但是,随着现代社会的发展,从高维数据中提取和识别威胁并应对未知的攻击类型是当前亟待解决的问题[1-2]。在异常检测领域,有两个被广泛接受的假设:①大多数数据行为是正常行为,只有少数行为是恶意行为;②攻击行为与正常行为有显着差异。在这两个假设条件下,目前,许多专家学者将多种类型的数据挖掘技术引入该研究领域,成为目前的热门研究[3-5]。近年来,许多专家在异常检测领域采用了一些聚类方法[6-9]。K-means是一种聚类方法,较早用于异常检测领域,但有其自身的局限性,例如聚类依赖性和简并性[10-12]。Y 均值法通过替换该方法生成的空聚类,消除离群值的影响以及合并相似的聚类以进一步优化聚类中心来改进k均值方法[13-16]。文中算法基于图的聚类算法,通常不需要考虑聚类中心的问题,具有处理大小、形状和密度不同的聚类的优势,并且对高维数据具有良好的效果。通过扩展共享的k最近邻的条件,提出了一种扩展的Jarvis-Patrick 聚类算法(Extended-Jarvis-Patrick,EJP),与其他聚类方法相比,文中算法更擅于发现强相关点的聚类。使用KDD Cup99 数据集进行实验,结果表明,与传统Jarvis-Patrick 聚类相比,该算法提高了检测率(Jarvis-Patrick的最佳检测率仅为78.7%,而EJP可以达到97.10%)。
1 Jarvis-Patrick聚类算法
Jarvis-Patrick 聚类算法的主要思想是首先找到每个数据点的k最近邻;其次,找到图中具有共享k最近邻关系的所有点。如果两个点具有共享的k最近邻关系,则这两个点之间可以有一条线,因此最终将获得一系列簇,其中每个簇中的点之间具有共享的k最近邻关系。该算法具有处理不同大小、形状和密度的簇的能力,并且对高维数据具有良好的效果。但是,在将算法应用于一些实际数据集之后,可以发现它仍然存在一些缺点。
通过将该算法应用于KDD Cup 1999 数据集,考虑到数据量较大,从数据集中随机抽取1 000、2 000和5 000 个数据点进行测试。根据前面提到的两个异常检测假设,α(累计值)应与标记为正常的点数一致,远大于聚类后的异常点数,因此取α=0.8。在α=0.8 处提取1 000、2 000 和5 000 个数据点时,使用Jarvis-Patrick 的最佳结果如表1 所示。可以看到,最好的检测率为78.7%。

表1 差异化数据点Jarvis-Patrick算法最佳结果
在对2 000 个提取的数据点进行测试时,检测率(Detection Rate,DR)和误报率(False positive Rate,FR)结果如图1 所示。图2 显示了在用不同的k值标记之前每个集群中的元素数量。

图1 Jarvis-Patrick聚类提取2 000个数据点时差异化k值的检测率(DR)和误报率(FR)(α=0.8)

图2 Jarvis-Patrick聚类提取2 000个数据点时标记前聚类大小分布(α=0.8)
图1 表明,当k=20时,检出率的最大值为0.787,并且可以看到,如果选择较小的k,则检出率要好于较大的k值,但最佳检出率为0.787。结合图2 可以发现,当k值较小时,每个群集中的点数是相对平均的,意味着大型群集和小型群集之间的大小差异不是很明显。随着k值的增加,大型群集的大小增加,太多的异常数据点将合并到大型群集中,并且在标记时可能会误判很多异常数据点为正常数据点,从而降低了检测率。
所以Jarvis-Patrick 聚类算法还存在以下缺点:
1)与其他基于图的聚类算法相比,Jarvis-Patrick算法本身的条件相对苛刻,只有两点之间具有共享的最近邻关系时,才能在它们之间存在一条边,因此聚类的结果似乎是零散的。也就是说,聚类结果中出现了太多的小型聚类。根据入侵检测的两个假设,只有一小部分数据被标记为异常点,因此,太多的小簇将对贴标过程的准确性产生负面影响;
2)当将Jarvis-Patrick 聚类算法应用于真实世界的入侵检测数据集时,其检测率和误报率均不令人满意。
为了解决这个问题,在传统的Jarvis-Patrick 聚类算法基础上,适当地控制了集群大小的增长,降低大型集群的增长速率,避免在没有太多小型集群的情况下出现误报率较低的结果,以便于获得合理的标记结果,从而提高检出率。因此,提出一种可以改善这些缺陷的改进的Jarvis-Patrick 聚类算法。
2 扩展Jarvis-Patrick聚类算法
通过上述实验得出,当k值较小时,Jarvis-Patrick算法具有较高的检测率,但是小聚类和离群值的数量太大,因此考虑扩展共享k最近邻条件。
定义1:扩展共享k最近邻
对于有向图G中的任意两点wp和wq,如果wp是wq的k最近邻,并且wq是(k+m)最近邻(其中m是任意整数),则在wp和wq之间存在一条边epq=
定义2:扩展共享k最近邻聚类图
由一组节点W={w1,w2,…wn}和边集E={e1,e2,…em}组成的有向图G称为扩展共享k最近邻聚类图,其中ei=
根据上面的定义,将共享k最近邻的概念扩展到Jarvis-Patrick 聚类算法。在完成聚类过程之后,能够获得扩展的共享k最近邻聚类子图。图3 所示为扩展的共享k最近邻关系的两个点P3和P4的示例。从图中可以看到,当k=4 且m=1时,P3具有4 个最近邻A、B、C和D,而P4具有4 个最近邻A、B、C和E,因此,当k=4时,设置m=1,则P4(k+m)的最近邻是A、B、C、D和E,因此,当k=4时,P3和P4可以在一个簇中。由此还可以看到,在相同的k值下,拟扩展共享k最近邻关系可以合并Jarvis-Patrick 原本分割的部分聚类,以减少最终聚类结果中的聚类数量。
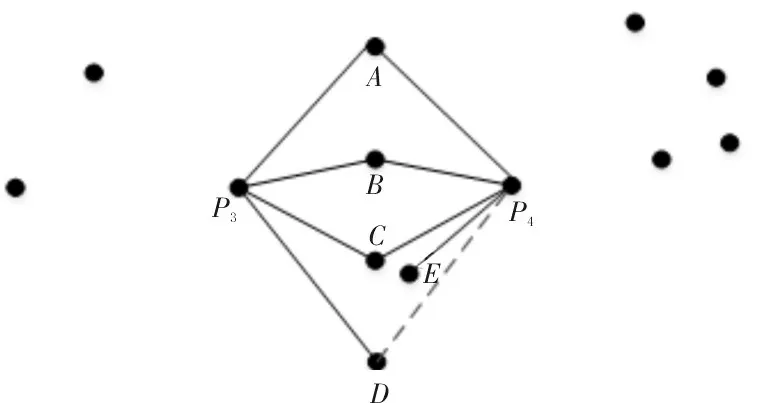
图3 k=4,m=1时,P3和P4的扩展共享k最近邻关系
在扩展Jarvis-Patrick 聚类算法(EJP)的步骤中,首先通过在每个点之间设置边来构造每个聚类,然后按升序累积每个聚类的大小。如果总累加值大于α%,则已经累加的群集将被标记为正常数据,而其他群集则被标记为异常数据。
3 仿真实验与分析
KDD Cup99 数据集包含连续数据和离散数据两种数据属性,不同的属性类型有很大的差异,因此,有必要在使用算法之前对数据的属性值进行归一化。归一化方法如下所示:
对于连续数据,使用式(1)进行归一化,首先,计算每个属性值的平均值和平均绝对偏移量:
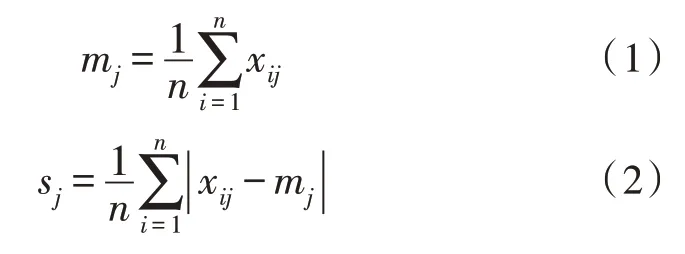
其中,n表示数据集中数据元素的总数,xij表示第i个数据的第j个属性值。因此,对应于该属性的归一化值为:

在某些情况下,从数据集中提取数据后,发现异常数据点过多,无法匹配上文提到的异常检测领域中的两个假设。因此,在这种情况下,如果需要,将会用从数据集中随机提取的正常数据替换一些异常数据。
实验中随机提取1 000、2 000 和5 000 个数据点,对扩展的Jarvis-Patrick 聚类算法进行测试。值得注意的是:①当m=0时,EJP算法就是Jarvis-Patrick算法本身;②根据前面提到的两个异常检测假设,α值应与标记为法线的点数一致,远大于聚类后的异常点数,因此取α=0.8。经过聚类和标记过程后,记录不同k值的每个聚类中的元素数量,以说明算法的效果。在此,选择了从数据集中提取的相同的3组数据。表2 显示了对这3 组数据进行实验后的最大检测率。值得注意的是,m可能为负数,因此计算(k+m)的值而不是k的值,并且使用正整数有助于研究准确率,从而减少统计量容易出错的问题。因此,在实验过程中,使用(k+m)的值,从而保留原始数据记录。
从表2可以看到,检测率有了很大提高。提取5 000个数据点时,最佳检测率高达97.1%。对于表2 中不同的m,EJP 不仅可以达到比传统Jarvis-Patrick 更高的检测率,而且对于其他k值,EJP 的检测率也高于传统Jarvis-Patrick 算法。对给定的k值选择不同的m值时,检测率变化如图4、5 所示。从图4 可以看出,k=20时,在m取不同值的情况下,最大检测率出现在m=20 或30处,检测率(DR)高达95%,远高于m=0 的检测率。当m=20(或m=30 或40)时,最大簇包含的点数大于m=0 时最大簇的点数。当k为其他较大的整数时,也可以得到同样的结果。图5 显示,当m=-50 或m=-10时,检测率(DR)达到最大值(95.7%),而当m=0时,检测率(DR)略高于60%。

图4 k=20和α=0.8时的检测率(DR)和误报率(FR)结果

图5 k=70和α=0.8时的检测率(DR)和误报率(FR)结果
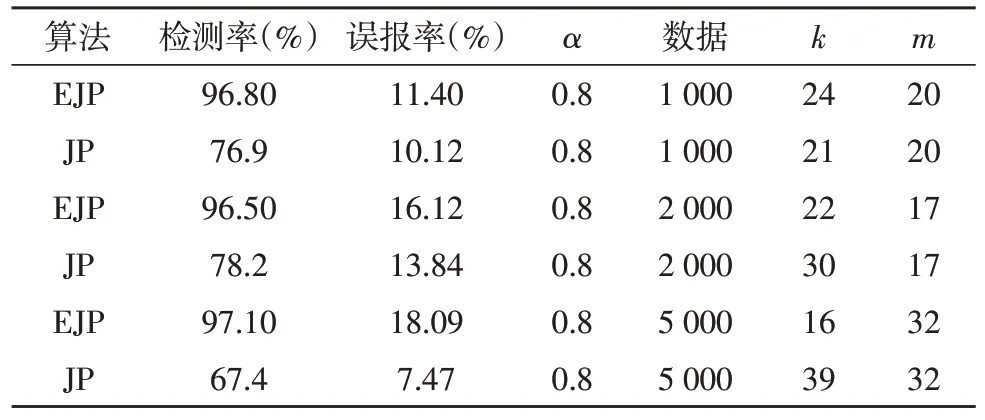
表2 扩展Jarvis-Patrick算法与传统Jarvis-Patrick算法结果对比
图6 显示了标记前EJP 聚类结果中聚类大小的分布(k=20,α=0.8)。在m=20(取最大检测率)时,大簇和小簇的大小具有显著差异,表明EJP 算法可以通过增加聚类大小差异来提高检测率。

图6 标记前EJP聚类结果中聚类大小的分布(k=20,α=0.8)
同样,当k为大值时,如图7 所示,当m为-10时,最大簇和最小簇之间的差异与m=0 相比有所降低,主要由于最大聚类和最小聚类之间的差异太大或聚类总数太小,从而导致检测率不足。尽管簇的大小差异并不明显,但是簇的总数增加,表明EJP 可以在较低误报率的情况下拆分Jarvis-Patrick 算法的某些簇,以实现较高的检测率。

图7 标记前EJP聚类结果中聚类大小的分布(k=70,α=0.8)
4 结论
该文将数据抽象为点,并确定两点之间的相似性,通过引入共享k 最近邻关系获得扩展的共享k 最近邻聚类簇,减少最终聚类结果中的聚类数量,降低数据量。通过在KDD Cup99 数据集进行验证,结果表明,该文优化算法可以很好地确定相似点属性,得到最佳聚类数并有效减少数据量。后续将为进一步提高算法的误报率进行研究。
