基于博弈论及机器学习的最优化算法设计与仿真

赵永亮，于倩，邓博，韩丽君，高红梅

（西安九天数智信息科技有限公司，陕西西安 710086）

近年来，科技的进步促使各种精密设备小型化、多功能化，相关的设计文件和图纸也越来越多[1-2]。如何快速分析设备故障发生的原因、制定故障解决对策成为一个热点问题。传统设备故障诊断主要依靠人工故障排除法，过于依靠经验丰富的专家且缺少对故障发生原因、位置、模式进行系统性的描述，故障解决过程相对较慢[3-5]。

目前，人工智能领域中机器学习发展迅速。作为一个重要的分支，深度学习因其出色的数据特征提取能力被广泛应用在目标识别等领域[6-8]。然而，随着人们对深度学习网络模型训练速度和数据处理能力要求的不断提升，基于单机模式的训练过程难以满足需求，分布式深度学习训练方法成为提升计算能力的有效途径[9-16]。

针对以上问题，该文提出基于博弈论及机器学习的最优化算法来实现设备故障诊断的快速响应。其利用海量、多类型数据作为故障诊断的样本数据，实现故障智能识别。

1 面向故障分析诊断系统的优化算法

故障分析诊断系统的目的在于通过数据和知识驱动，实现设备故障的产生机理分析与故障预警等功能，达到资源与能源利用效率最高的目的。而优化算法则是提升海量数据、案例内容数据处理能力的重要技术，关系到故障分析诊断的速度和精度。文中通过对设备设计原理、关键元器件、故障事件信息、故障维护信息以及设备日常监测数据等核心信息的梳理，构建了设备知识图谱，并以此为故障诊断模型的训练样本；利用深度学习网络构建故障诊断模型，提高对知识图谱的数据挖掘能力；最后将博弈论（GT）引入到分布式深度学习网络计算资源的分配策略中，提高了深度学习网络模型的计算能力。具体流程如图1 所示。

图1 故障诊断流程示意图

深度学习是机器学习的一个重要分支，通过模拟人类大脑神经元之间传递、处理数据的模式，进行海量数据潜在逻辑关系的分析挖掘。与人类神经网络不同的是，深度学习是一种多层神经网络，具有输入层、隐藏层和输出层，具体结构如图2 所示。其中，为了达到最佳的“学习”效果，通常需要有多层隐藏层。但是隐藏层的增多，层与层之间的网络参数也随之增多，训练过程将变得复杂。因此，合适的隐藏层层数和神经元个数决定着故障诊断的精准度，也影响着诊断时间的长短。文中引入博弈论来确定隐藏层层数和神经元的个数，来实现最佳的故障诊断优化算法。

图2 深度学习网络结构示意图

利用深度学习网络来进行设备故障的快速诊断需要其具有一定的计算资源，通常由于计算能力和能源、资源的限制，导致无法较好地执行密集型计算任务。针对这种现象，文中采用分布式深度学习模型进行模型的训练，并将博弈论和移动边缘的卸载策略相结合，将不同计算节点有策略地纳入训练中，实现训练效率的提升。分布式深度学习网络的最佳训练卸载问题是一个具有多种约束条件（时延小、能耗小）的优化问题，基于此可将优化算法的目标函数设置为能量消耗最低、时间延迟最小的训练数据卸载策略问题。图3 为针对上述优化问题设计的算法流程。

图3 分布式深度学习模型训练数据卸载算法流程图

2 算法设计

2.1 知识图谱的构建和应用

为了快速响应对故障原因、模式等情况的分析，需要构建各个设备的知识图谱，如图4所示。第一步，在相关专家的指导下围绕该设备进行概念建模，包含了设备设计原理、关键元器件、故障事件信息、故障维护信息等核心概念，并输出Schema定义。第二步，根据Schema 定义将相关内容划分为结构化、半结构化和非结构化数据，并进行知识抽取。第三步，利用抽取的结果进行知识融合。依据实体对齐、类型对齐以及合计属性对齐的原则，建立知识之间的关联关系。为了保证融合的有效性，将相关领域的专业术语、技术规范作为参照标准。第四步，将融合后的知识图谱按照应用功能、场景进行分类存储，形成全方位的故障知识库。

图4 设备故障知识图谱构建流程示意图

图5 为基于知识图谱的故障诊断推理框架示意图，将海量的知识图谱作为深度学习网络的样本数据，参与故障诊断模型的训练。由于知识图谱中数据量较大，且当设备发生故障时，需要较快地诊断响应速度。因此文中采用分布式深度学习网络进行故障诊断模型的构建，并将博弈论引入到分布式计算资源的分配，实现深度学习网络模型的优化。

图5 基于知识图谱的故障诊断推理框架示意图

2.2 基于博弈论和深度学习的最优化算法

如图6 所示，深度学习网络的基本结构为RBM，RBM 为两层结构：输入层、输出层。在进行深度学习网络模型训练时，需要对网络参数进行初始化。这些参数有输入层、输出层的偏置参数a、b和RBM网络结构中神经元之间的连接权重w。合理且合适的初始化参数可以避免模型训练时出现梯度消失或梯度爆炸的情况，进而提高故障诊断的识别率。文中采用极小值随机初始化的方式，并在Matlab 软件环境中进行上述参数的初始化，公式如下：

图6 基于深度学习网络的故障诊断模型示意图

式中，n、m分别代表可视层和隐藏层中神经元的个数。zeros(m,1)函数代表产生向量元素全部为0的n×1 阶矩阵。normrnd(0,0.01,[m,n])函数可生成服从正态分布（0,0.01）的随机m×n阶矩阵。

确定参数初始化数值后，需要确定隐藏层层数和每层隐藏层的神经元个数，文中引入博弈论进行隐藏层和神经元个数的选择。在博弈论中，需要形成一种所有参与者均满意的方案，这种策略组合被称为纳什均衡。因为潜在博弈至少有一个NE解，NE的确定可以等价表示为所有计算节点的单个函数的优化。文中定义了一种非合作博弈，具体形式为h(N,M,A,G)。其中，N为隐藏层层数，M为神经元个数，A为深度学习网络执行策略，G为收益函数。文中采用数据并行的分布式深度学习并行策略，即每次模型训练时，随机选择多个小批量的训练数据在不同的计算节点上进行模型训练。其具体训练流程为：

1）每个计算节点分别从通信网络上或者硬盘上读取一定容量的数据，并发送至内存中；

2）将数据从CPU 内存转移到GPU 内存中，并加载CPU kernel，使得深度学习网络模型由前向后逐层进行计算；

3）计算损失函数，并启动反向传播，逐层计算梯度值；

4）更新各个计算节点的梯度值，并基于新的梯度值更新神经网络参数。

以上过程即为深度学习网络模型的一次训练过程，又被称为一次迭代。将数据保存在不同计算节点内存的过程分为本地执行和卸载到异地执行。本地执行的成本函数仅受到设备CPU 频率Flocal的影响，本地执行计算任务Ci的时间和能量消耗为：

式中，elocal为每个CPU 在单个计算周期内消耗能量的系数。卸载到异地执行即将计算任务卸载到相邻计算节点，该方式下的时间延迟和能量成本分别为：

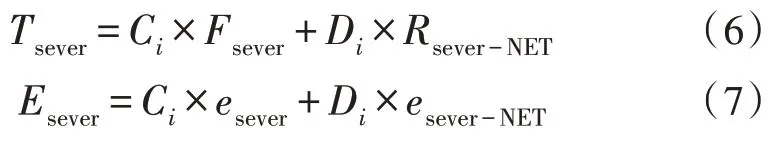
3 测试与验证

该节基于Matlab 软件，通过数值仿真来验证文中基于博弈论和深度学习的最优化算法的有效性。文中使用的软硬件环境配置如表1 所示。

表1 计算机软硬件配置

Matlab 仿真环境的设置如下：模拟分布式深度学习网络训练任务的卸载数据量大小为[100,800]kbits，每计算1 bit所花费的周期为476 cycles/bit。隐藏层层数和神经元个数对故障诊断准确度的影响如图7 所示。

图7 隐藏层层数和神经元个数对故障诊断准确度的影响

从图7 中可以看出，隐藏层层数和神经元个数的增加均会提高故障诊断的准确度，并且不同的隐藏层层数条件下，诊断准确度均会稳定在一定的数值。这表明分布式深度学习网络模型是稳定的。值得注意的是，隐藏层层数的增加可使分布式深度学习网络模型更快地达到收敛值。因此，文中深度学习网络被设置为4 层隐藏层、每层各40 个神经元。

在进行博弈论非合作博弈策略验证时，假定每个计算任务的最大时延服从均匀分布U[2,10]，其时延单位为s，每个计算节点最初均为本地执行任务状态。当有密集型训练任务时，每次均可以选择最优计算卸载策略作为优化算法中下一次决策迭代的唯一更新。图8 为求解NE解的分布式深度学习网络的性能评估情况。从图中可以看出，在经历了有限次迭代后，分布式深度学习网络优化算法会逐渐收敛到某个值，该值为博弈的平衡点，证明了NE解的存在。

图8 GT的收敛性

图9 为不同优化策略系统总消耗的比较，TOS 为总卸载方案，GOS 为基于深度学习的卸载方案，GT为基于博弈论的分布式深度学习卸载方案。其中，TOS 是将所有的计算任务均下发至系统服务器；GOS 利用深度网络考虑了传输数据量的大小和网络条件，但并未考虑数据传输所造成的系统延迟和能量消耗。从图中可以看出，随着任务数据量的增多，3 种优化算法的总消耗均有所上升，但是基于GT 的优化策略显著低于另外两种优化算法。与对照组相比，文中方案将系统总消耗降低了18.9%。

图9 不同优化策略算法下系统总消耗的比较

4 结束语

文中针对精密设备故障诊断响应速度慢的问题，通过将深度学习、博弈论和移动边缘计算相结合，以时间消耗与能量消耗为优化目标，提出了基于博弈论及深度学习网络的故障诊断最优化算法。经测试，文中所述方案与其他优化算法相比，显著降低了系统能量的消耗。