基于多矩阵AHP的无人机自主作战能力灰色评估
2022-07-08王晓光王小平刘树光尚永爽
王晓光,杜 军,王小平,刘树光,尚永爽
(1.空军工程大学航空工程学院,陕西 西安 710038;2.空军工程大学装备管理与无人机工程学院,陕西 西安 710051;3.中国人民解放军93184部队,北京 100076)
0 引言
无人机技术的逐渐成熟推动了无人机的大量应用。在军事领域,无人机逐渐应用于情报侦察、信息传输、对地攻击等方面,展现出了巨大的军事价值和应用潜力[1]。时至今日,各国军队都开始大量编配使用无人机,相关工业部门也加紧了无人机技术攻关和型号研制,无人机在装备体系中的地位日益重要。同时,伴随着无人机智能化和自主化水平的不断提升,其承担的任务也日趋多样化,可以说无人机已经成为作战样式变革和装备体系更新换代的重要源动力之一。
目前来看,无人机自主执行作战任务是未来战争的一个重要趋势[2-4]。部分研究机构和学者也开始了无人机自主作战能力评估的相关工作。美军在其报告《Unmanned Aircraft System Roadmap 2005-2030》中率先提出了无人机自主作战等级分类方法[5],并得到了广泛认可;但这一报告只是将无人机自主作战能力定性地划分为10个等级,并没有给出相对精确的无人机自主作战能力评估方法。文献[6]建立了无人机自主作战能力评估体系,给出了无人机自主作战能力试验架构,但是试验评估往往成本较高,周期较长,并且评估过程难免存在一定主观性。文献[7]从设计角度开展了高空长航时无人机的作战能力评估工作,并建立了一种基于对数法的无人机作战能力评估体系,但是这种方法对评估数据精度要求较高,工程应用效果欠佳。文献[8]用一种改进的Hopfield神经网络从感知能力、决策能力、行为能力和安全能力4个方面开展了对地攻击型无人机的自主作战能力评价工作,从工程实用性的角度完成了对地攻击型无人机自主作战能力的量化评价,但是这种方法无法满足多任务能力无人机的评估要求。本文针对上述问题,在构建无人机自主作战能力评估体系的基础上,结合改进的层次分析法(analytic hierarchy process,AHP)和灰色系统理论完成无人机的自主作战能力评估。
1 无人机自主作战能力评估体系构建
无人机的自主作战能力评估体系来源于具体的作战使用需求。对于无人机来说,与作战使用需求息息相关的指标主要包括平台性能指标、指挥控制指标、任务载荷指标、链路通信指标、突发事件处理能力指标等[9-11],基于互质原则得到自主作战能力评估体系如图1所示。
无人机的自主作战能力评估需要在构建得到评估体系的基础上,通过综合运用仿真计算、厂家试飞、部队试验、对抗演练等评估手段,采集相关评估数据,进而得到评估结果。显然,在同一评估体系下,针对同一评估目标,不同评估手段可能会得到不同的评估结果。为保证评估结果的准确性和可信度,有必要对不同评估手段得到的评估结果进行融合。
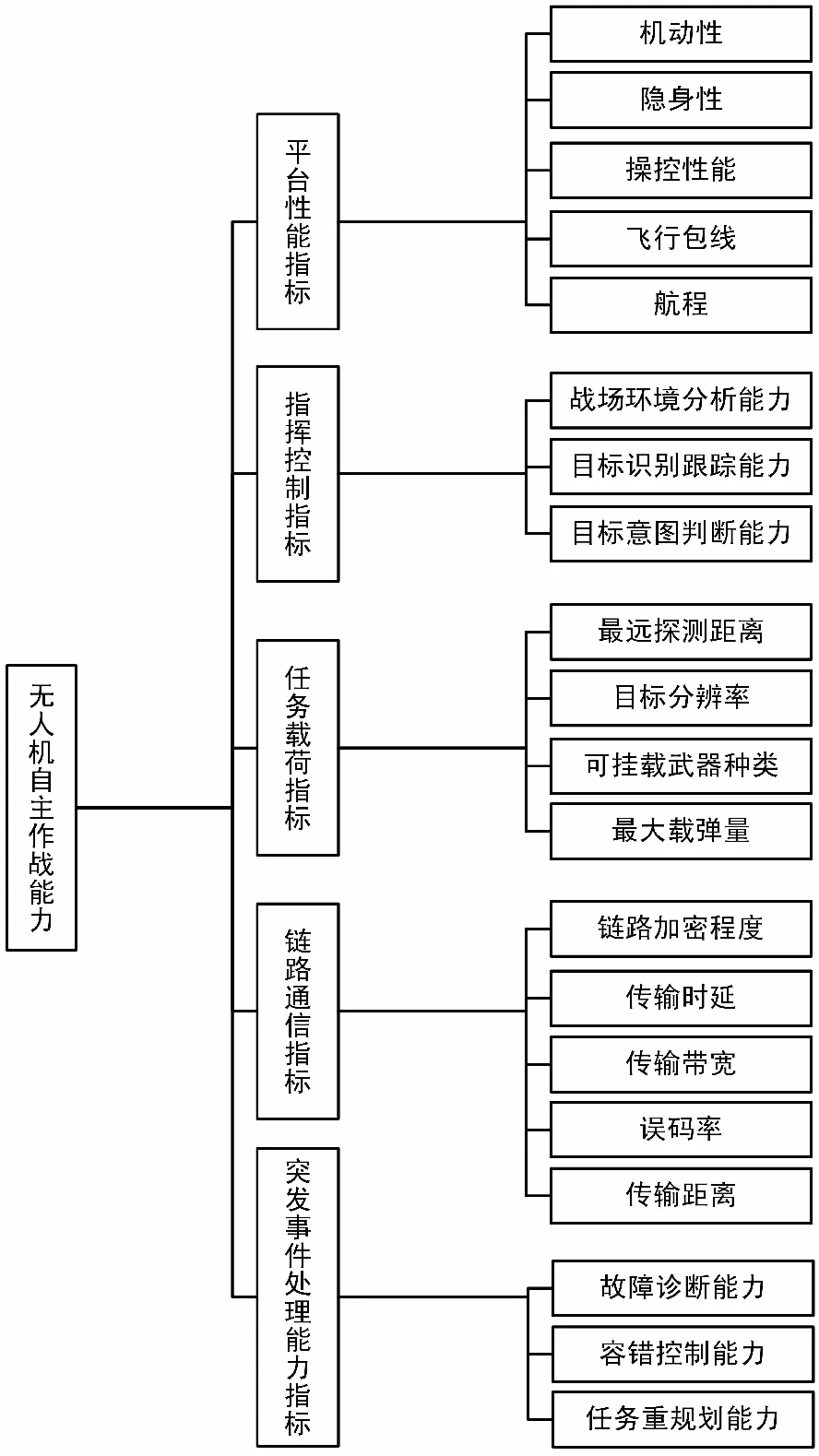
图1 无人机自主作战能力评估体系Fig.1 Evaluation system of UAV’s autonomous combat capabilities
2 基于多矩阵AHP的灰色评估
2.1 多矩阵AHP方法
在装备作战能力评估体系中,权重用来表示不同指标之间的重要性差异。AHP方法能够根据待评估对象的性质,将评估目标分解为多个评估要素,是一种描述各评估指标重要性差异的有效方法,在评估领域得到了广泛应用[12-13]。但是,传统的AHP方法其权重判断矩阵只有一个,并且权重判断矩阵只由一名或一组专家评分得到,显然这种方法难免存在较大的主观性。
专家评分的主观性将直接影响到无人机自主作战能力评估体系中各指标的权重,继而会影响到无人机自主作战能力评估结果的准确性。因此,本文对AHP方法进行相应改进,通过引入多名或多组专家,来计算得到多个权重判断矩阵,以此来尽可能地减少AHP方法中存在的主观性。
2.1.1权重判断矩阵构建
权重判断矩阵本质上是各名/组专家对各个评估指标相对重要性的比较和分析。一般情况下,专家按照9级分制原则进行打分[14],打分的标准及含义如表1所示。

表1 专家打分标准及含义Tab.1 Expert scoring criteria and implications
若专家打分为2,4,6,8则表示该项指标重要性是上述相邻判断的中值。
如果集合m名/组专家对n项指标进行打分,最终可以得到m个权重判断矩阵A1,A2,…,Am,其中,第k名/组专家的权重判断矩阵为:
(1)
式(1)中,k=1,2,…,m,并且满足akji=1/akij,akij>0,akii=1,其中i,j=1,2,…,n。
2.1.2权重系数计算
权重系数计算的目的是为了得到m名/组专家的权重判断偏好。工程上通常采用方根法、和积法等方法进行权重系数计算。以和积法为例,具体步骤如下:
1) 对权重判断矩阵Ak按列规范,计算得到
(2)
由此可以计算得到第k名/组专家的权重系数向量Wk=[wk1,wk2,…,wkn]T。与此类似,可以得到其他m-1名/组专家的权重系数向量。显然,这m个权重系数向量代表了m名/组专家的权重判断偏好。
2.1.3一致性检验与权重系数平均
由于AHP方法中的权重判断矩阵是由专家主观赋值得到,其中可能存在一定的逻辑自洽性问题,因此,AHP方法还必须对计算得到的权重系数进行一致性检验。
第一步,计算过渡矩阵:
(3)
第二步,计算λkmax,具体算法为:
(4)
得到λkmax后再求取检验算子CR,具体算法如下:
(5)
检验算子CR为判断权重判断矩阵一致性的指标;RI称为修正因子,RI具体取值从表2中查表得到[14]。
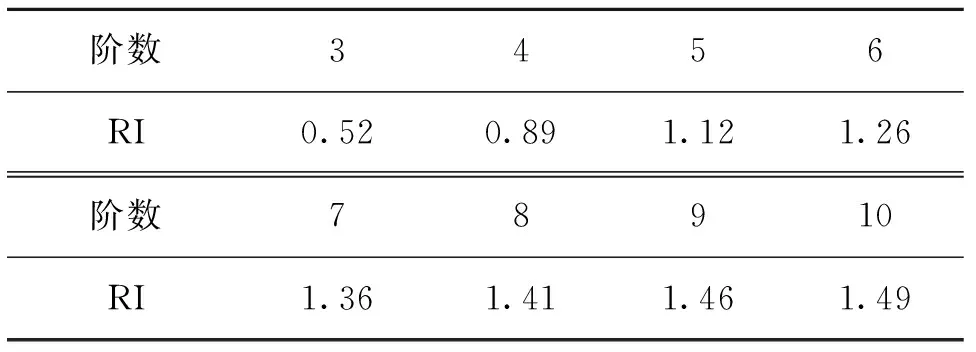
表2 修正因子与阶数对应表Tab.2 Correction factors and orders corresponding table
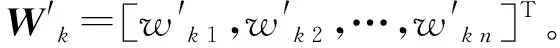
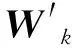
(6)
W′即为多专家权重系数向量,显然W′融合了m名/组专家的权重判断信息,相对于经典AHP方法来说,这种多矩阵AHP方法具备较强的客观性和可信度。整个多矩阵AHP算法的计算流程如图2所示。
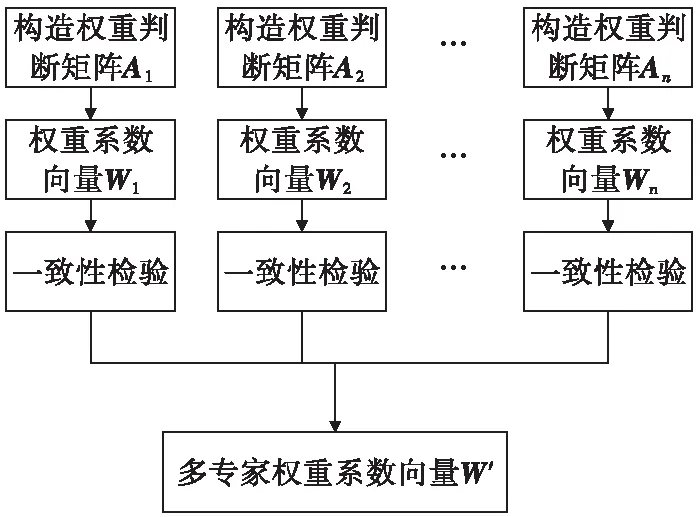
图2 多矩阵AHP算法流程图Fig.2 Thealgorithm flow chart of multi-matrix analytic hierarchy process
2.2 灰色评估
无人机作战中的某些信息很难进行准确测度和衡量,如果不加处理地直接根据这些信息进行评估,结果势必存在较大偏差。为得到较为准确的无人机自主作战能力评估结果,有必要采用灰色系统理论进行无人机的自主作战能力评估。
灰色系统理论主要以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定系统为研究对象,通过对部分已知信息的生成、开发,提取有价值信息,实现对系统运行规律的正确描述和有效评估[15-16]。结合无人机自主作战能力评估指标体系,给出灰色评估方法如下。
2.2.1确定无人机自主作战能力评估灰类
为保证评估结果的准确性,无人机自主作战能力通常采用多种评估手段进行综合评估。无人机作战能力评估方法比较多[17-19],假设采用P种方法来给平台性能指标C1、指挥控制指标C2、任务载荷指标C3、链路通信指标C4、突发事件处理能力指标C5共5项指标进行计算评分,分值范围为0~10分。如果第p(p=1,2,…,P)种方法给指标Cq(q=1,2,…,5)的计算评分结果为dqp,那么可以得到无人机自主作战能力评估样本矩阵D:
(7)
得到评估样本矩阵后就可以计算评估灰类。评估灰类是一个可供比较的类别或概念,具有模糊性和不确定性,为了描述灰类,需要确定相应的灰数和对应的白化权函数。灰数是指一个大概的范围,通常记为⊗。
如果将无人机自主作战能力划分为优、良、中、次、差5个档次,那么对应的就有5个灰类的评价等级,分别记为e=1,2,3,4,5。各灰类的灰数和白化权函数如下所示。
① 灰类e=1,灰数⊗1∈[7,9,∞),其白化权函数表达式为:
(8)
对应的白化权函数如图3(a)所示。
② 灰类e=2,3,4,灰数⊗2∈[4,7,10],⊗3∈[2,5,8],⊗4∈[0,3,6]其白化权函数表达式为:
(9)
对应的白化权函数如图3(b)所示。
③ 灰类e=5,灰数⊗5∈[0,1,3],其白化权函数表达式为:
(10)
对应的白化权函数如图3(c)所示。
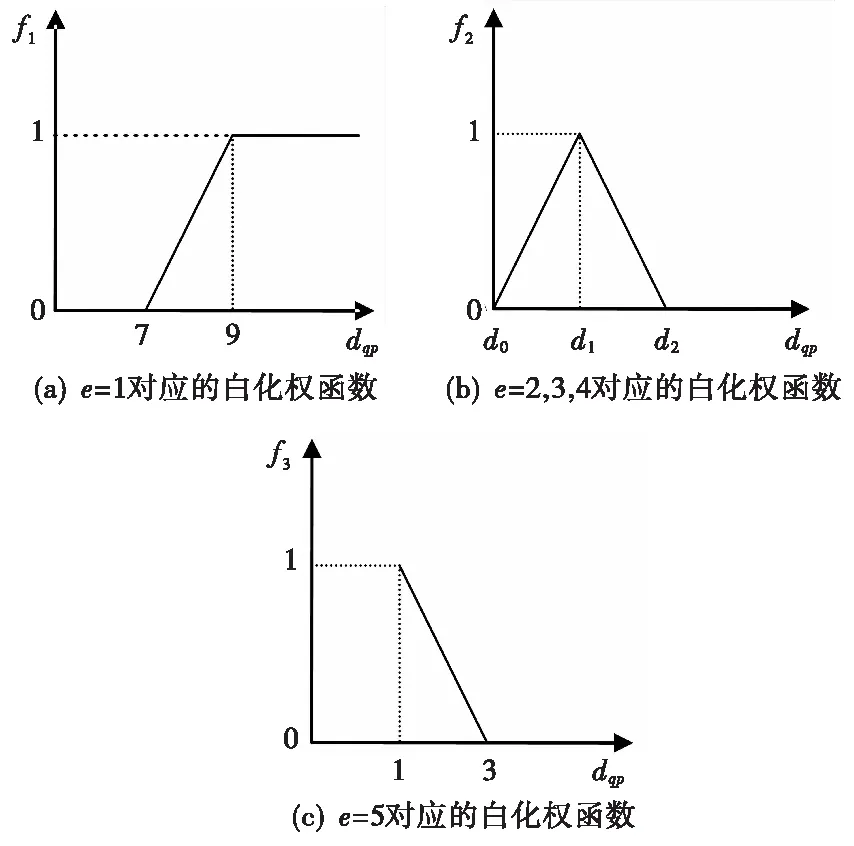
图3 各灰类的白化权函数Fig.3 The whitening weight functions of thegrey classes
当e=1时,按照式计算评估样本矩阵D中元素对应的灰类白化权函数,得到白化权矩阵E1;同理,e=2,3,4按照式计算D中元素对应的灰类白化权函数,得到白化权矩阵E2,E3,E4;e=5按照式计算D中元素对应的灰类白化权函数,得到白化权矩阵E5。由于白化权函数的输入是评估样本矩阵D,那么白化权矩阵维数与评估样本矩阵D相同,均为5行P列。
2.2.2确定无人机自主作战能力评估值
得到白化权矩阵后,就可以进行无人机自主作战能力评估值的计算。
首先,将计算得到的每一个白化权矩阵分别按列相加,得到灰色评估系数向量re,re中元素re(q)计算方法为:
(11)
显然,re为列向量,e=1,2,3,4,5。
然后,计算得到灰色评估矩阵R,R中元素R(q,e)算法为:
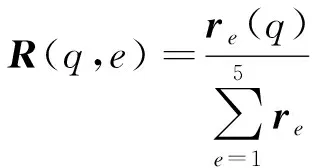
(12)
R中的一列就代表了一个评估系数向量在评估系数向量之和中所占比重。
最后,通过结合多专家权重系数向量W′和灰色评估矩阵R,计算得到灰类评估结果B,即
B=W′·R。
(13)
给定e=1,2,3,4,5对应的评分向量
S=[s1,s2,s3,s4,s5]T,
(14)
则最终可以得到无人机自主作战能力评估值为:
E=B·S。
(15)
整个评估算法流程如图4所示。
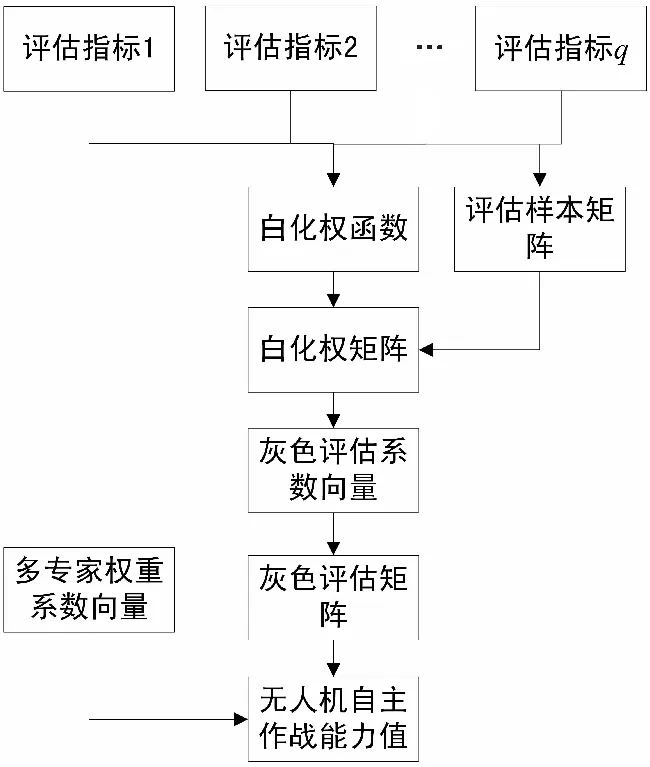
图4 无人机自主作战能力评估算法流程Fig.4 The evaluation algorithm flow of UAV’s autonomous combat capabilities
3 算例分析
本文假设有3名/组专家对无人机自主作战能力评估体系中的平台性能指标、指挥控制指标、任务载荷指标、链路通信指标、突发事件处理能力指标5项指标的相对重要度进行评分比较,然后采用4种估算方法对无人机的自主作战能力进行估算,在此基础上,进行算例分析。
首先,计算多专家权重系数向量W′。如果3名/组专家对5项指标给出的权重判断矩阵分别为:
那么,经过权重系数计算、一致性检验等操作后,可以得到对应的3个权重系数向量:
结合式(6),得到多专家权重系数向量:
W′=[ 0.181 1,0.367 6,0.056 9,0.183 8,0.361 4]T。
然后,结合W′和灰色系统理论进行无人机自主作战能力评估。若4种不同估算方法对无人机的5项自主作战能力指标的估算结果为:

那么,对应5个评价等级,就有5个白化权矩阵:
在此基础上,计算得到灰色评估矩阵
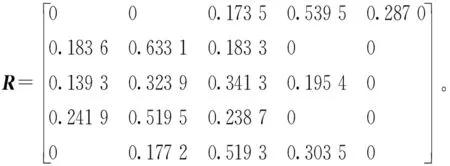
最后,给定评分向量S=[9,7,5,3,1]T,结合式(13)-(15),可以求得在多专家权重系数向量W′基础上的无人机自主作战能力评估值为E=6.409 9。显然在10分制评价体制下,该无人机的自主作战能力仅处于合格水平。其主要原因在于多专家权重系数向量W′中最大项为第5项,对应突发事件处理能力指标。但从矩阵D中的第5行突发事件处理能力估算结果来看,其最大值为5.971 3,最小值仅有3.787 4,均值仅为4.703 8,因此尽管该无人机的指挥控制指标和链路通信指标等指标估算结果较好,但是,该无人机的综合自主作战性能评分不高。
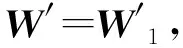
4 结论
本文提出基于多矩阵AHP方法和灰色系统理论的无人机自主作战能力评估方法。通过引入多名/组评估专家来构建多专家权重系数向量,以此削弱评估指标相对重要性判断中的主观因素,提高权重系数向量的可信度;采用灰色系统理论来减少不同评估方法带来的评估偏差和评估过程中的不确定性;结合多矩阵AHP方法和灰色系统理论得到评估结果。算例分析结果表明该评估方法能够实现多名/组评估专家对评估指标相对重要性判断结果的有效融合,同时也能够实现多种无人机自主作战能力评估方法和结果的有效融合,该方法适用面较广,可用于无人机设计、试飞和对抗演练等不同场景和需求,具有较高的推广应用价值。
