电和电磁环境对引信全电子安全系统的影响
2022-07-08汪仪林马秋华
汪仪林,马秋华
(西安机电信息技术研究所,陕西 西安 710065)
0 引言
随着引信全电子安全系统的大量使用,亟需评估电和电磁环境对其安全性的影响,进而按照GJB 373B—2019《引信安全性设计准则》[1]、GJB 346A—2019《引信安全失效率计算方法》[2]等要求计算安全失效率,分析电/电磁环境对全电子安全系统的影响是评估安全失效率的重要环节,目前国内尚未开展相关研究,故亟需加强此项工作。本文以GJB 573B—2020《引信及引信零部件环境与性能试验方法》[3],GJB 151B—2013《军用设备和分系统电磁发射和敏感度要求与测量》[4],GJB 7073—2010《引信电子安全与解除保险装置电磁环境与性能试验方法》[5]等标准规定的电和电磁环境为可信环境,分析其对引信安全性的影响;基于全电子安全系统的电路结构,通过建立初级/次级传递函数,分析GJB 573B—2020《引信及引信零部件环境与性能试验方法》[3]及GJB 151B—2013《军用设备和分系统电磁发射和敏感度要求与测量》[4],GJB 7073—2010《引信电子安全与解出保险装置电磁环境与性能试验方法》[5],GJB 8848—2016《系统电磁环境效应试验方法》[6]等标准规定的电和电磁效应作用下在高压电容或雷管上产生的电压;根据电压幅度和起爆概率的关系,确定对安全失效率的影响。在典型的电路参数下,以典型的全耦合变压器为例,计算对安全性影响较大的静电、电流传导和电压传导在高压电容和雷管上产生的电压,说明在两个静态开关和动态开关(三个开关)均处于短路状态时CS114规定的传导电流、CS106规定的传导电压可能导致安全失效。
1 静电、电缆注入和电源电压传导对全电子安全系统安全性影响分析
1.1 电起爆器电压特性和安全失效率的关系
全电子安全系统的基本构成选用2016年第59届国际引信年会论文中的典型电路[7],如图1所示。
为了方便分析和讨论,只保留与安全状态有关的部分,如图2所示。
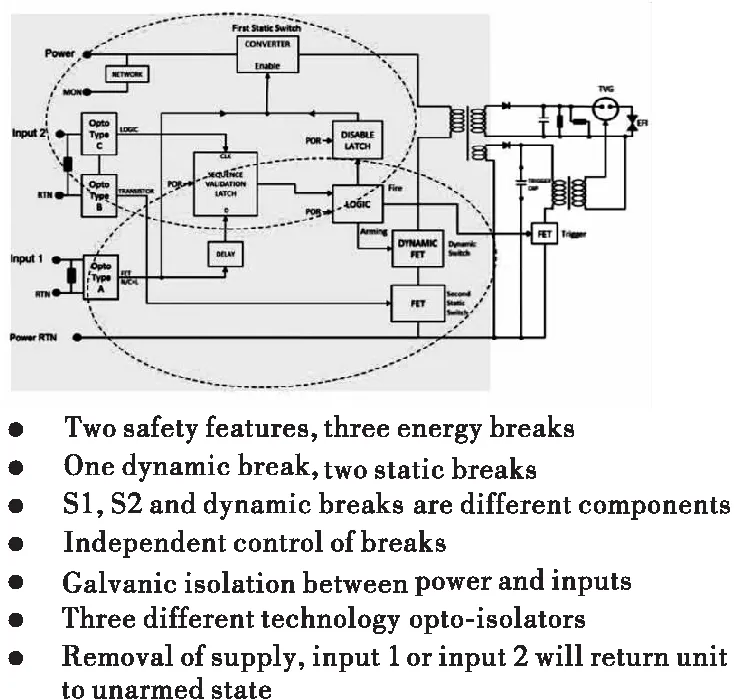
图1 典型全电子安全系统框图Fig.1 The typical schematic diagram of electronic safety-and-arming system
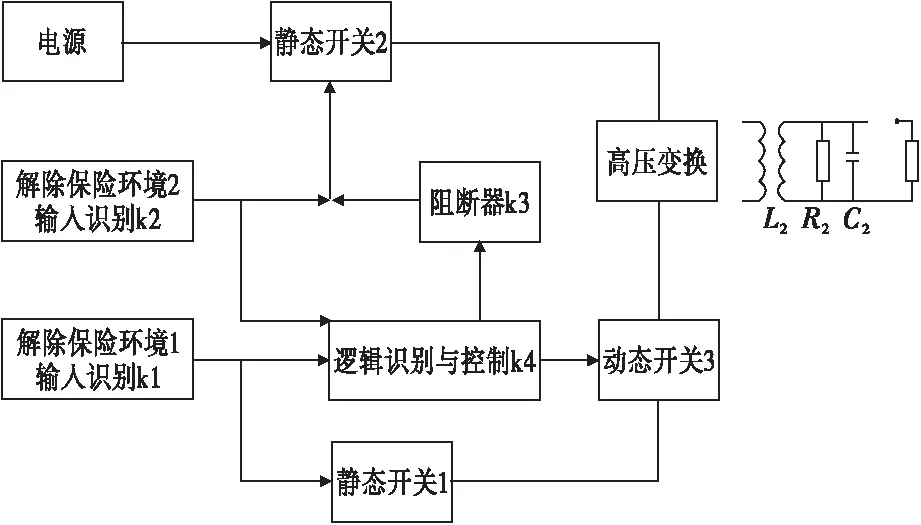
图2 全电子安全系统框图Fig.2 The schematic diagram of electronic safety-and-arming system
其工作过程为:解除保险环境识别k1识别第一解除保险环境后输出控制信号,驱动静态开关1闭合;解除保险环境识别k2识别第二解除保险环境后,由逻辑控制器k4对解除保险环境时序进行时序判断,符合预定时序要求时使阻断器k3释放,静态开关2闭合;在满足规定的延时要求后,产生交替变化的信号控制动态开关,高压变换器在交变信号的驱动下进行高压变换,开始对高压电容充电,解除隔离。本文中高压变换采用全耦合变压器。
基于电雷管起爆的正态分布特征,电雷管起爆概率Pd1为:
(1)
式(1)中,μ为期望值,σ为方差,Vd为高压电容器电压。
设雷管起爆电压为V1,起爆电压达到V0(V0≥500 V),引信处于已解除隔离状态,由此求得该雷管起爆电压分布:
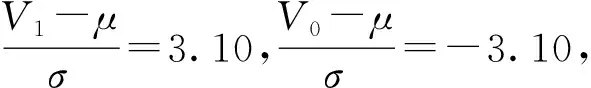
雷管起爆概率低于百万分之一对应的电压Va为:
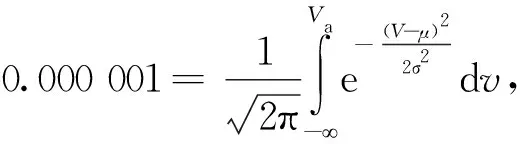
1.274V0-0.274V1。
若V1=1 200 V,V0=500 V,则:μ=850 V,σ≈112.9,Va≈308.1 V。
通过式(1)可以算出雷管或高压电容两端电压对应的起爆概率。
1.2 静电、电流注入和电源尖峰等激励在高压电容上建立的电压
通常引信安全系统都有屏蔽壳体,通过辐射等方式对安全性的影响远低于引线上传导的电流、电压和静电馈入。因此我们主要考虑GJB 151B—2013《军用设备和分系统电磁发射和敏感度要求与测量》[4]中的CS114、CS115、CS116、CS106和GJB 573B—2020中静电对安全性的影响。
高压变换次级和电源通过变压器隔离,故不考虑电源及电源地传导的影响,只考虑典型引线方式下,静电和电缆束注入在高压电容和雷管上建立的电压。初级回路分析考虑静电、电流和电压传导的影响。
1.2.1静电、电流源对雷管放电在雷管上建立的电压Udg计算
静电对雷管放电的电路示意图如图3所示。
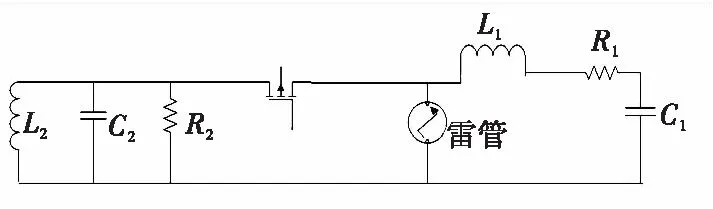
图3 静电对雷管放电示意图Fig.3 The diagram of electrostatic discharge to detonator
建立放电回路微分方程
(2)
式(2)中,L1、C1、R1为静电放电电感、电容、电阻,rL为雷管等效电阻,i(t)为流入雷管的电流(即放电电流)。
对式(2)进行拉普拉斯变换得到:
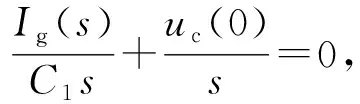
(3)
式(3)中,uc(0)为静电放电电压。
由式(3)可得:
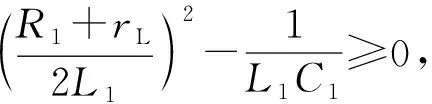
(4)
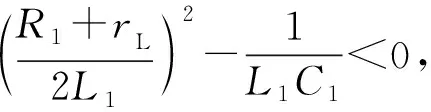
(5)
静电在雷管两端建立的电压为Udg,Udg=ig×rL。
若电流注入,注入电流为Ii,在电雷管两端的电压则为:Udi=Ii×rL。
1.2.2静电、电流源在高压电容上建立的电压Ucg、Uci计算
与高压电容相关的静电引入途径(高压电容通过引线拉出壳体再和高压开关连接)如图4所示。
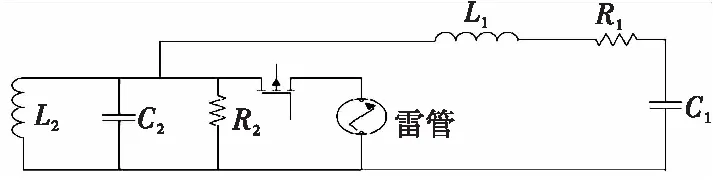
图4 高压电容和高压开关连接点通过引线拉出壳体时静电引入示意图Fig.4 Electrostatic discharge diagram of high-voltage capacitance and high-voltage link to shell with cable
1) 计算静电在高压电容上建立的电压Ucg
式中,Icg为放电电流。
则有:
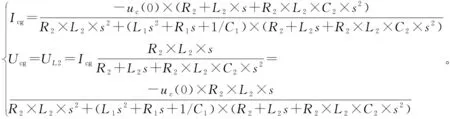
(6)
2) 计算电缆线电流注入在高压电容上产生的电压与高压电容相关的电流注入途径如图5、图6所示。
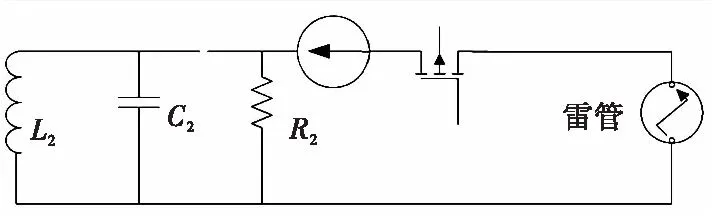
图5 高压电容和高压开关连接点通过引线拉出壳体时线上电流注入Fig.5 Current injection diagram of high-voltage capacitance and high-voltage link to shell with cable
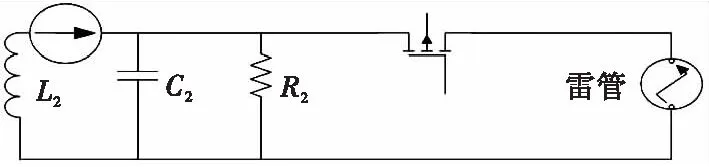
图6 高压变换和高压电容之间引线拉出时电缆线电流注入Fig.6 Current injection of cable link to voltage transformer and high-voltage capacitance
图5为在高压开关入口引出线,图6为在高压电容端引出线。分别计算这两种引线方式在电流注入下,高压电容上产生的电压。
图5所示电流注入在高压电容上建立的电压计算如下:
(7)
式(7)中,Ii为注入电流的拉普拉斯变换,R0为电流源注入等效内阻。
图6所示电流注入在高压电容上产生的电压计算如下:
(8)
1.2.3输入回路静电、电流注入和电源尖峰在高压电容上建立的电压计算
按照设计要求,不应将静态开关、动态开关放置在不同的电路板上,所以不考虑静电、电流从静态开关之后引入的情况。
输入回路如图7所示,图中R1、C1,R2、C2,R3、C3分别为静态开关1、静态开关2和动态开关在未开启时的等效电阻、电容,其值和所用开关类型和参数有关,在后续例子中将会加以说明。
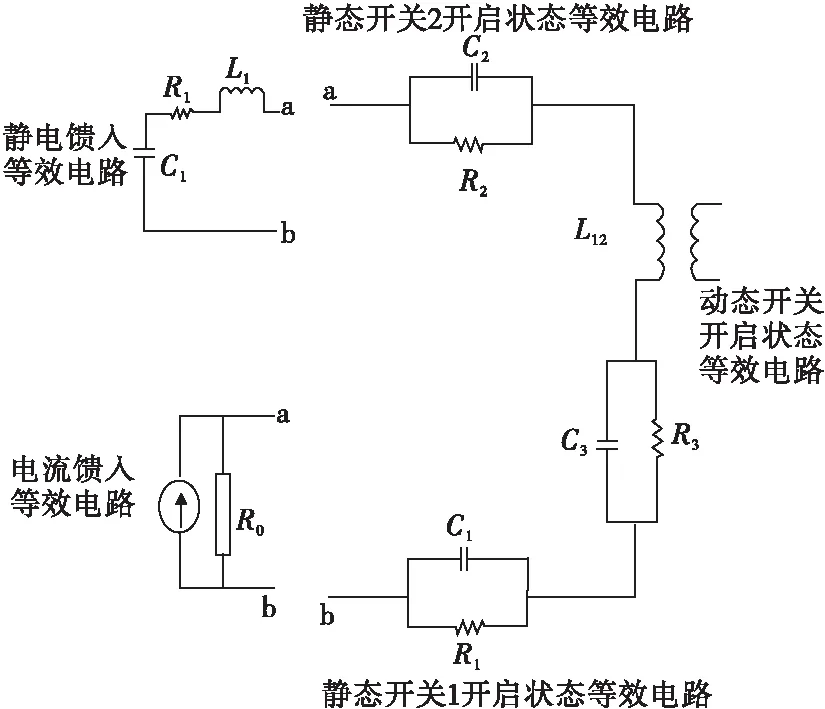
图7 初级回路静态开关、动态开关和高压变换示意图Fig.7 Diagram of static switch,dynamic switch and voltage tansformer of the primary circuit
次级回路对前级回路的影响用和电感L12并接的阻抗ZL表示,对于全耦合变压器则有
(9)
式(9)中,n为初级/次级变压比。
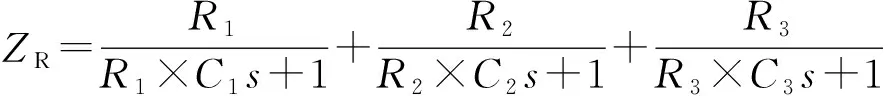
(10)
(11)
1) 计算初级回路静电在高压电容上建立的电压
次级等效阻抗上形成的电压
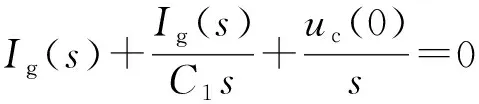
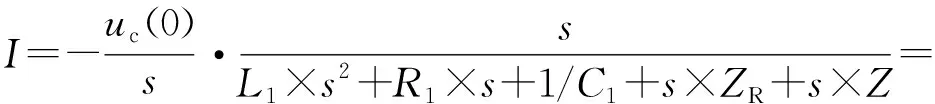
等效阻抗ZL上建立的电压
(12)
在高压电容上建立的电压为:
(13)
令Ug123为ZR符合式(10)(即3个开关均处于开启状态时)由式(12)、式(13)计算的结果,将求出的电压值代入式(1),得到概率P(Ug123/n);
Ug12、Ug13、Ug23分别为R3、R2、R1为0(即1个开关出现短路故障或解除时)的计算结果,将求出的电压值代入式(1),得到P(Ug23/n)、P(Ug13/n)、P(Ug12/n);
Ug1、Ug2、Ug3分别为R2、R3,R1、R3,R1、R2同时为0(即2个开关出现短路故障或解除时)的计算结果,将求出的电压值代入式(1),得到P(Ug1/n)、P(Ug2/n)、P(Ug3/n);
Ug为R1、R2、R3同时为0(即3个开关出现短路故障或解除时)时的计算结果,将求出的电压值代入式(1),得到P(Ug/n)。
2) 计算初级回路电流注入在高压电容上建立的电压
初级回路电流注入在次级等效阻抗上形成电压计算如下:
(14)
式(14)中,Ii为注入电流。
电流注入在高压电容上建立的电压为:
(15)
令Ui123为ZR符合式(10)(即3个开关均处于开启状态时)由式(14)、式(15)计算的结果,将求出的电压值代入式(1),得到P(Ui123/n);
Ui12、Ui13、Ui23分别为R3、R2、R1为0(即1个开关出现短路故障或解除时)计算的结果,将求出的电压值代入式(1),得到P(Ui23/n)、P(Ui13/n)、P(Ui12/n);
Ui1、Ui2、Ui3分别为R2、R3,R1、R3,R1、R2同时为0(即2个开关出现短路故障或解除时)计算的结果,将求出的电压值代入式(1),得到P(Ui3/n)、P(Ui2/n)、P(Ui1/n);
Ui为R1、R2、R3同时为0(即3个开关出现短路故障或解除时)时的计算结果,将求出的电压值代入式(1),得到P(Ui/n)。
3) 计算初级回路电源尖峰在高压电容上形成电压
初级回路电源尖峰在次级等效阻抗上形成电压
(16)
式(16)中,Uv为电源线传导电压。
电源线传导电压在高压电容上建立的电压
(17)
令Uv123为ZR符合式(10)(即3个开关均处于开启状态时)由式(16)、式(17)计算的结果,将求出的电压值代入式(1),得到P(Uv123/n);
Uv12、Uv13、Uv23分别为R3、R2、R1为0(即1个开关出现短路故障或解除)时计算的结果,将求出的电压值代入式(1),得到P(Uv23/n)、P(Uv13/n)、P(Uv12/n);
Uv1、Uv2、Uv3分别为R2、R3,R1、R3,R1、R2同时为0(即2个开关出现短路故障或解除)时计算的结果,将求出的电压值代入式(1),得到P(Uv3/n)、P(Uv2/n)、P(Uv1/n);
Uv为R1、R2、R3同时为0(即3个开关出现短路故障或解除)时的计算结果,将求出的电压值代入式(1) 得到P(Uv/n)。
2 全电子安全系统失效率计算
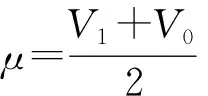
参照1.1节给出的全电子安全系统,静态开关1采用双极型晶体管,静态开关2采用晶闸管,动态开关采用硅场效应晶体管。
设静态开关1未闭合时的等效电阻R1=1 MΩ,等效电容C1=50 pF;静态开关2未闭合时的等效电阻R2=500 kΩ,等效电容C2=C1;动态开关未闭合时的等效电阻R3=1 MΩ,等效电容为C3=100 pF。
初级/次级变压比(n)=变压器(高压变换器)初级电压/次级电压=25/2 000=1/80;若采用全耦合变压器,初级和次级的电感比为L12=n2×L2,L2=500μH;高压电容C2=0.2μF。
耗散电阻R2=50 MΩ,雷管等效电阻rL=0.5 Ω。
进行静电计算时,根据GJB 573B—2020《引信及引信零部件环境与性能试验方法》[4]的人体静电条件取C1=500 pF,L1=5 μH,R1=5 Ω,uc(0)=25 kV;进行CS116、CS114计算时将等效电流源内阻取为R0=1 000 Ω。
2.1 计算静电、电流源在雷管上建立的电压Udg、Udi
静电在雷管两端建立的电压为Udg,Udg=ig×rL。
将电路参数代入式(4)、式(5):
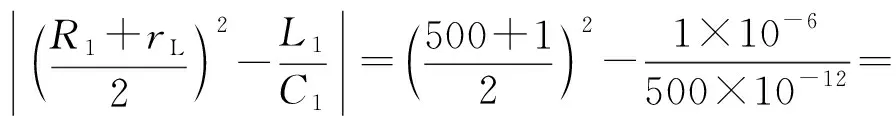
ig的幅度为:
由于rL<1,Udg≪123 V,可忽略其影响。
若电流注入,注入电流可为Ii,在电雷管两端的电压则为:Udi=Ii×rL。
GJB 151B中CS114、CS115和CS116注入电流峰值均不大于10 A,雷管等效阻抗rL通常小于1 Ω,故在雷管上建立的电压低于10 V,在安全失效分析中,可略去其影响。
2.2 静电、电流源在高压电容上建立的电压Ucg、Uci计算
将电路参数代入式(6)计算在高压电容上产生的电压Ucg,结果如图8所示。
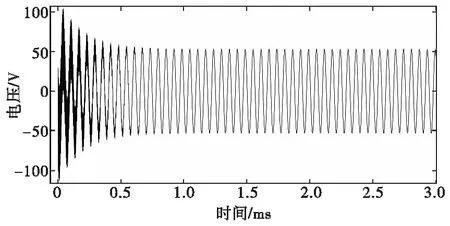
图8 人体静电在高压电容上产生的电压Fig.8 Voltage of personnel-borne ESD at the high-voltage capacity
Ucg≪123 V,可忽略其影响。
将电路参数代入式(7)、式(8),求GJB 151B—2013的CS116正弦阻尼瞬变电流[4]注入在高压电容上产生的电压Uci。CS116的注入电流为i≈I0e-αtsin (ω0t),ω0在10 kHz~10 MHz频率范围内,由式(7)、式(8)计算出的Uci分别如图9(a)、图9(b)所示。由图可知Uci≪123 V,可忽略其影响。
为了求GJB 151B—2013的在4 kHz~400 MHz CS114电缆束注入下,雷管两端注入电流时高压电容的响应曲线,先计算高压电容两端注入电流时的传递函数,计算结果如图10(a)所示,雷管两端注入电流的传递函数如图10(b)所示。
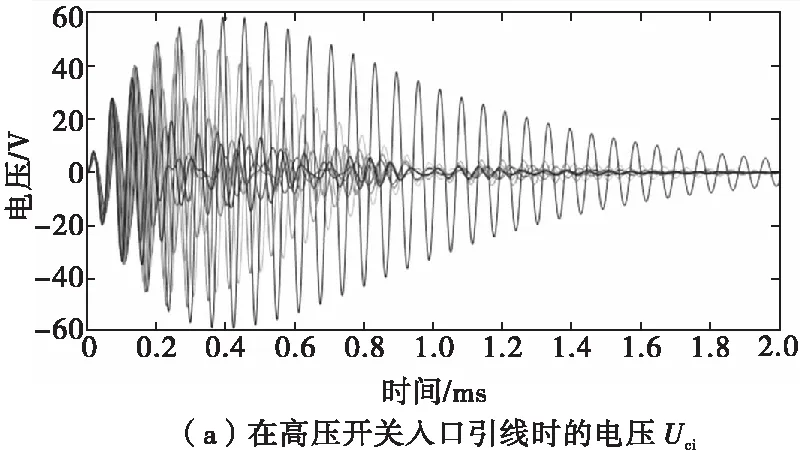
图9 CS116正弦阻尼在高压电容上产生的电压Fig.9 Voltage of CS116 sine impedance at the high-voltage capacity
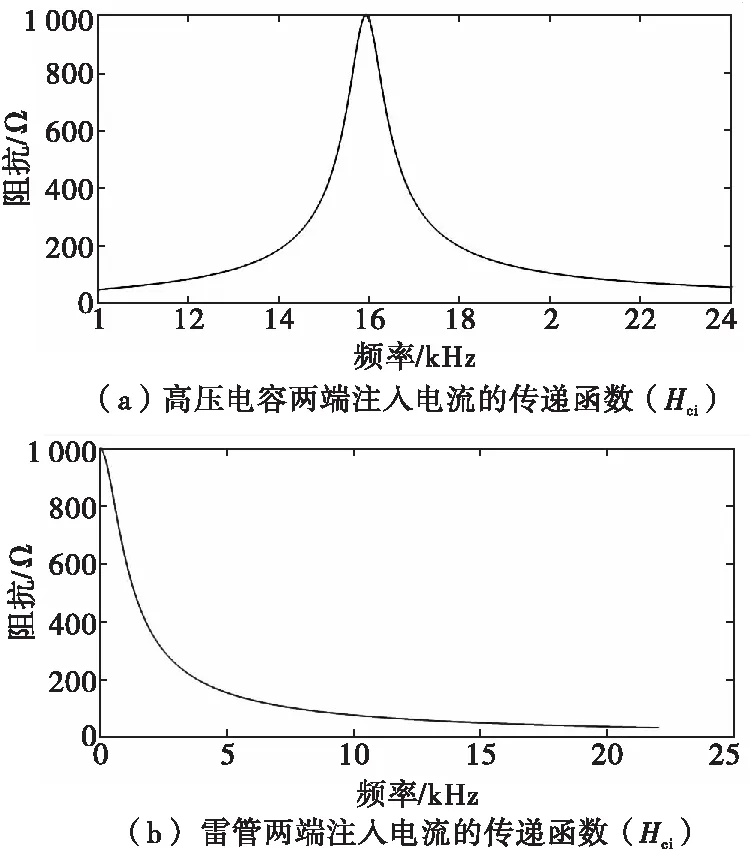
图10 两种电流注入下的阻抗曲线Fig.10 The impedance diagram of two kinds of current injection
从图10可见,阻抗最大值为1 000 Ω,图10(a)对应频率约16 kHz,图10(b)对应频率为0 Hz。
CS114在1~30 MHz频率注入电流为109 dBμA(即0.282 A),由图10可知该频段对应传递函数的模小于100,可得电压幅值不大于28.2 V;CS114在16 kHz时,注入电流约73 dBμA(即4.466 mA),该频段对应传函的模约1 000,可得电压幅值不大于4.5 V。CS114注入电流在高压电容上建立的电压远小于123 V,可忽略其影响。
上述计算表明在高压回路(次级回路)中,人体静电及按照GJB 151B给出的电流、电压传导,都不会在高压电容或雷管上建立超过123 V的电压,故可忽略其对安全性的影响。
2.3 计算初级回路静电、电流源、电压干扰在高压电容上建立的电压Ucg、Uci 、Ucv
1) 计算人体静电从初级电源端引入,在高压电容上产生的电压Ucg
由式(12)得人体静电在次级等效阻抗上产生的电压如图11所示。图中Ug123为静态开关、动态开关均正常的电压,Ug23为静态开关1发生短路故障时的电压,Ug3为静态开关1、2均发生短路故障时的电压,Ug为两个静态开关、一个动态开关均发生短路故障的情况。
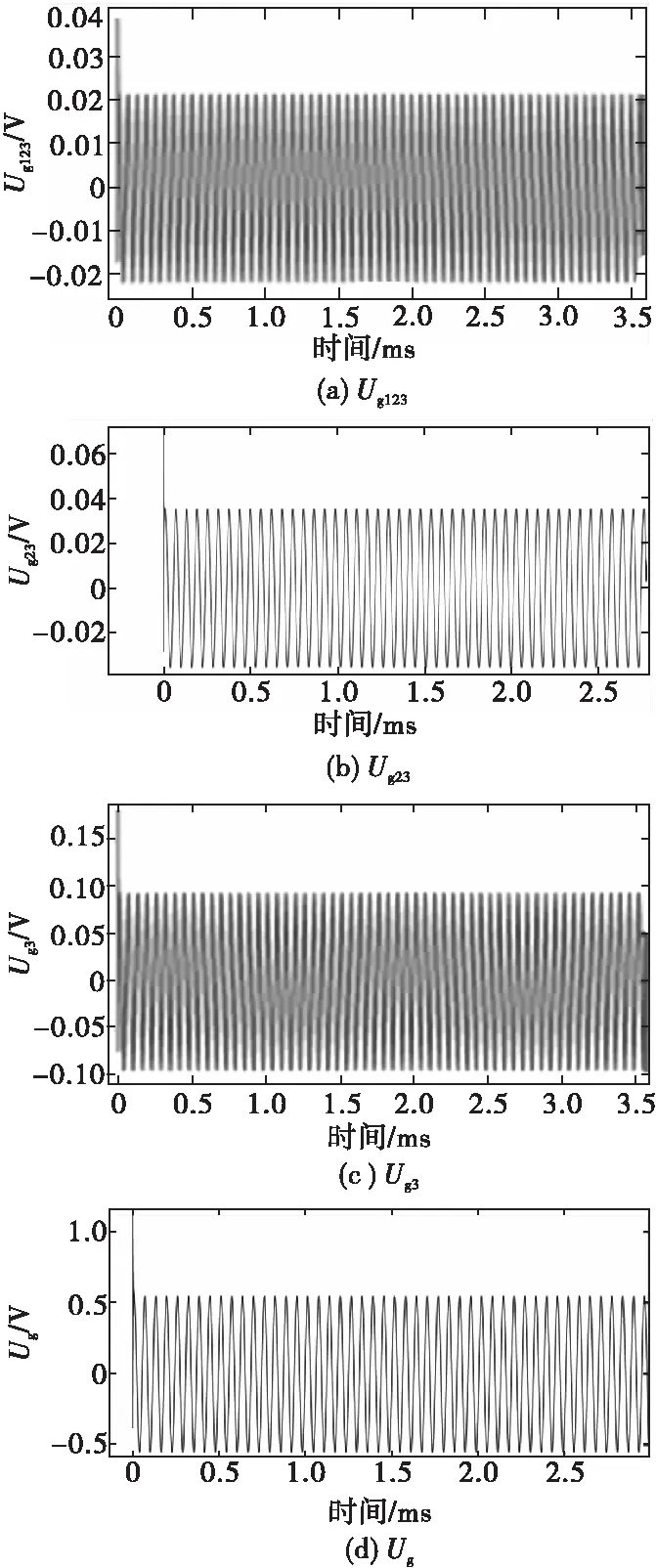
图11 初级回路引入静电在次级等效阻抗上产生的电压Fig.11 Voltage of the secondary equivalent impedance through ESD of the primary circuit
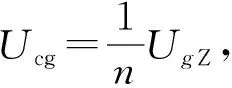
2) 计算GJB 151B中CS114电流注入时,在高压电容上建立的电压Uci
由式(14)得电流源激励在次级等效阻抗上产生电压的传递函数频响曲线如图12所示,Hi124、Hi23、Hi3、Hi分别为静态开关均正常、一个静态开关发生短路故障、两个开关发生短路故障、三个开关均发生短路故障。
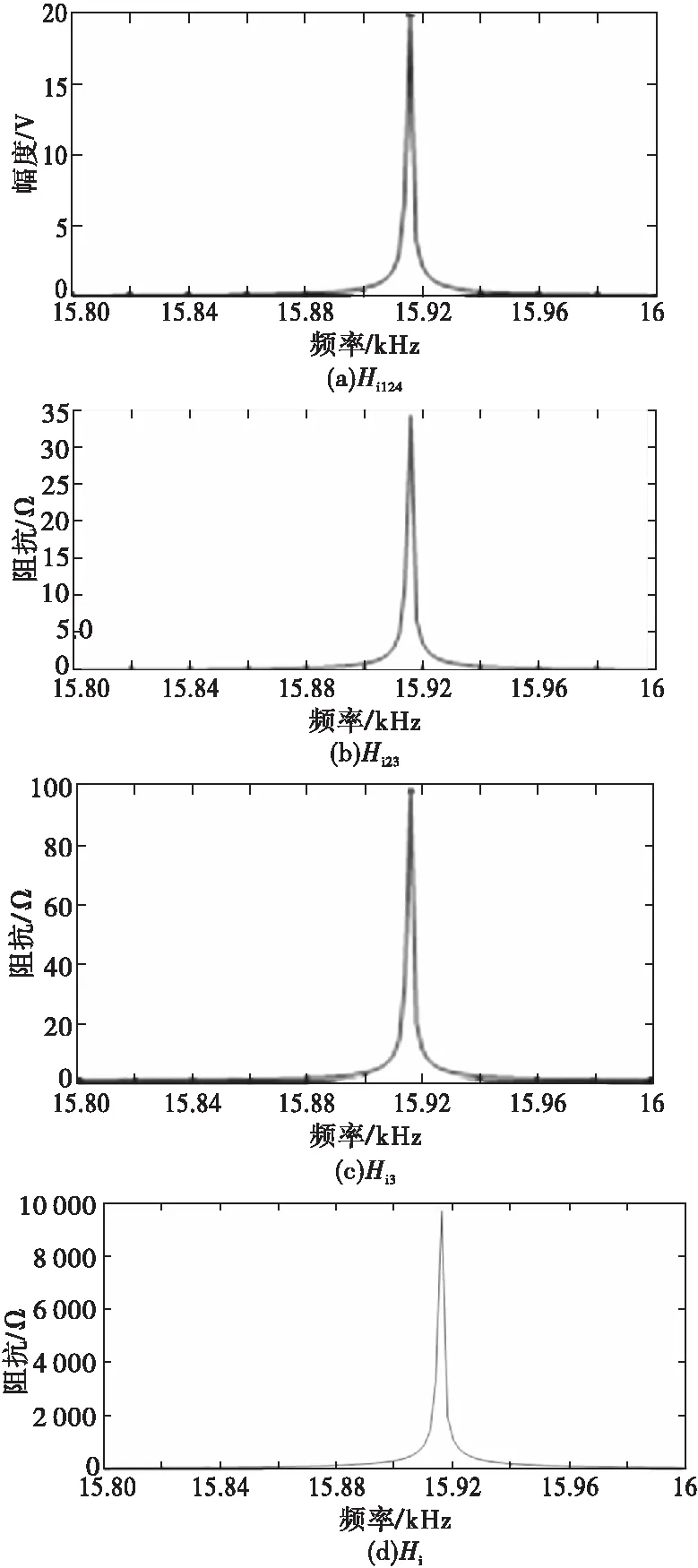
图12 初级回路电流注入在次级等效阻抗上产生电压的传递函数Fig.12 Transmit function of the secondary equivalent impedance through injection of the primary circuit
CS114在1~30 MHz频率注入电流为109 dBμA(即0.282 A),由图12(d)知该频段对应传递函数Hi的模小于5,电压幅值不大于1.41 V,在高压电容上建立的电压1/n×1.41=112.8 V,小于123 V,可忽略其影响;CS114在15~16 kHz时,注入电流约73 dBμA(即4.466 mA),该频段对应传递函数的模大于9 000,可得电压幅值约40 V,由式(15)得在高压电容上建立的电压Uci=1/n×40=3 200 V,大于123 V,达到雷管起爆电压,安全失效。
3) 计算GJB 151B中CS116电流注入时,在高压电容上建立的电压Uci
由式(14)得电流瞬变在次级等效阻抗上产生的电压如图13所示,Ui123、Ui23、Ui3、Ui分别为静态开关均正常、一个静态开关发生短路故障、两个开关发生短路故障、三个开关均发生短路故障。
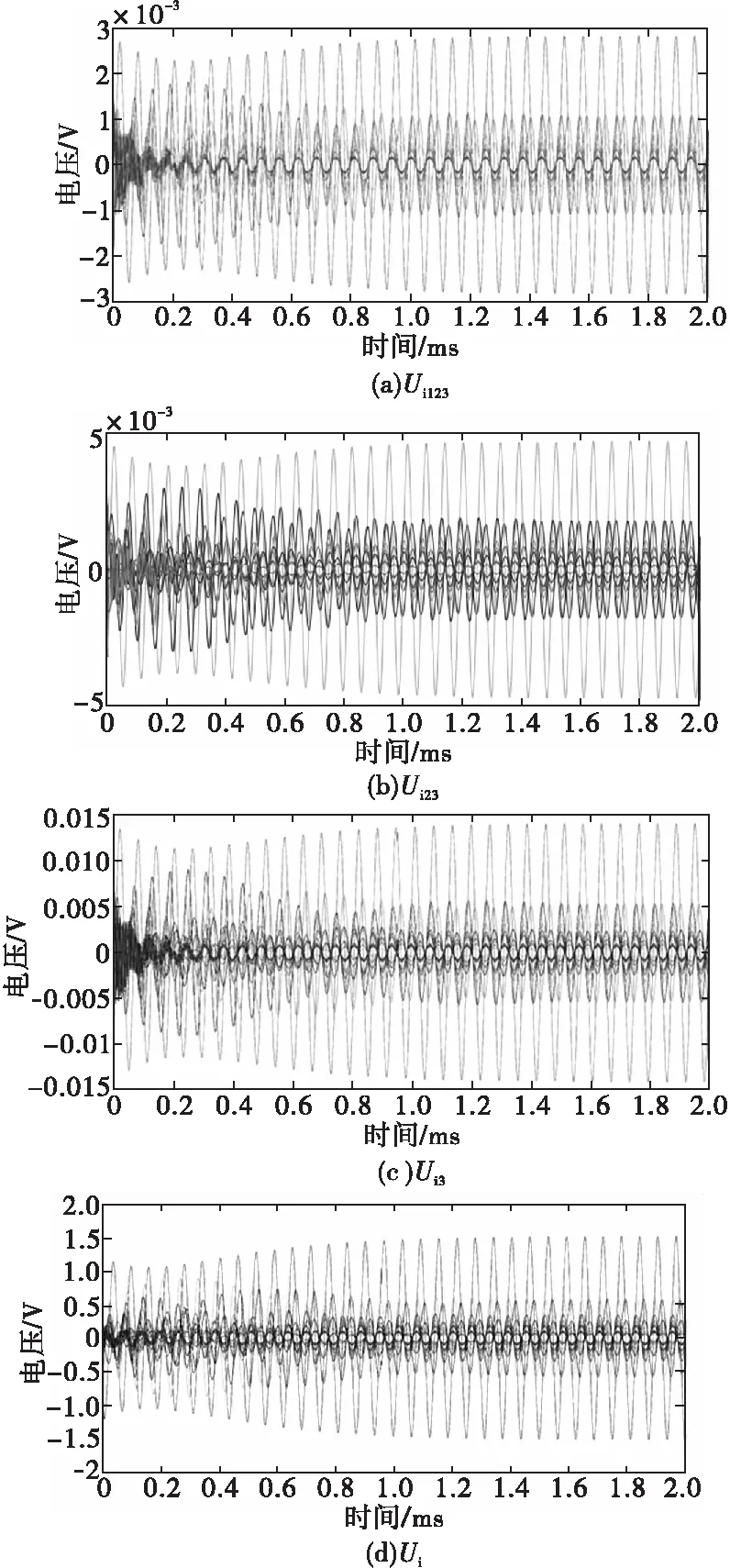
图13 初级回路注入正弦瞬变电流在次级等效阻抗上产生的电压Fig.13 Voltage of the secondary equivalent impedance through sine instantaneous current through the primary circuit
图13(d)电压幅值不大于1.5 V,在高压电容上建立的电压Uci=1/n×1.5=120 V,小于123 V,可忽略其影响。
4) 计算初级回路电源串扰在高压电容上产生的电压Ucv
由式(16)得初级回路电源尖峰在高压电容上电压响应的传递函数如图14所示,Uv123、Uv23、Uv3、Uv分别为静态开关均正常、一个静态开关发生短路故障、两个开关发生短路故障、三个开关均发生短路故障。

图14 初级回路电源串扰在高压电容上产生的电压Fig.14 Voltage of the high-voltage capacitances through current disturb of the primary circuit
图14(d)电压幅值达400 V,在高压电容上建立的电压Ucv=1/n×400达到起爆雷管电压,安全失效。
上述计算表明,在至少一个开关未闭合时,一般的电和电磁效应并不导致安全失效率的降低,但当三个开关出现短路故障,且出现电流注入和电源线尖峰信号传导时(如图12(d)、14(d)所示),会导致安全失效。因此,设计应确保避免此类现象的发生。
3 讨论
3.1 高压回路中静电放电对全电子安全系统的影响
若静电放电条件变为直升机补给静电:
E=±300 kV,C=1 000 pF,R1=1 Ω,L=10 μH,雷管端静态电阻为1.0 Ω时得
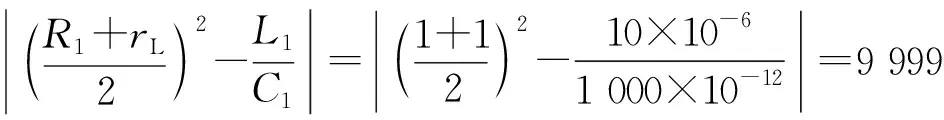
则有,ig=3 000×e-7×104tsin (107t)静电放电在雷管上产生的电压Udg=3 000×e-7×104tsin (107t)。
若雷管端静态电阻为0.5 Ω时,
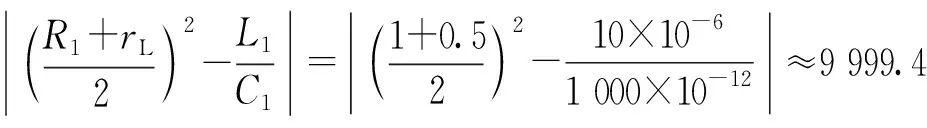
在雷管上产生的电压Udg=1 500×e-7×104t·sin (107t),最大值超出123 V,达到起爆雷管所需的电压。
因此,要高度重视高压回路的静电防护,确保弹体表面可能产生的静电放电没有引入全电子安全系统高压回路的潜在通道,采取的防护措施应确保在高压电容或雷管端产生的电压满足安全裕度要求。
3.2 初级回路的防护
第2章计算了静电、电流注入、电源电压瞬变等在高压电容上产生的电压,得出了至少有一个开关处于未闭合状态时这些激励不影响安全性的结论,但如果三个开关均处于短路状态则有可能安全失效。计算静电、电流注入、电源电压瞬变产生的总电压,考虑篇幅略去推导,直接给出静电在三个开关上产生的总电压如图15(a) 所示;电源电压瞬变在三个开关上产生的总电压如图15(b)所示;正弦阻尼电流注入在三个开关上产生的总电压如图15(c )、(d)所示,其中(c )对应频率低于1 MHz的情况,(d)对应频率在1 MHz以上的情况。
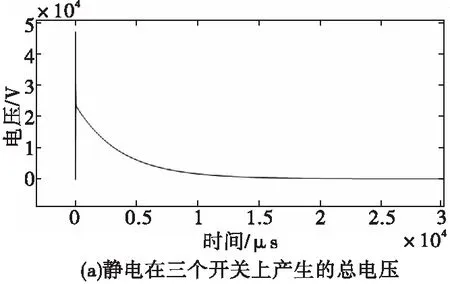
图15 初级回路在高压电容上的总电压Fig.15 The total voltage at thigh-voltage capacitance of the primary circuit
图15(a)、(c )、(d)表明,在开关上可产生超过千伏的瞬态电压,引信设计中若选用静态开关、动态开关的总耐压不够,三个开关可能同时发生电压击穿,而诱发三个开关同时闭合的失效模式进而导致安全失效。
因此,初级回路的瞬态电压防护至关重要,应确保可信的电/电磁激励下防护措施有效,一方面应满足三个开关中耐压最低器件耐压裕度要求,另一方面应保证耦合到高压电容端的电压在安全裕度以内。
4 结论
以国际引信年会发表的引信全电子安全系统为例,分析了全电子安全系统主要电/电磁环境影响因素,推导了不同激励参数条件下的传递函数,得出了在不同位置引入静电、电流注入和电源线传导在高压电容和雷管上产生电压的计算方法,将典型电路参数代入计算可知:在正常情况下这些因素基本上不影响安全性,但是当三个开关因故障而处于短路状态,按GJB 151B馈入CS114、CS106规定的电能时,可能会导致安全失效。计算了静电、电流注入和电源线传导在三个开关上产生的电压:当三个开关总耐压不够时,可能会发生三个开关因击穿而处于短路状态导致安全失效。因此,全电子安全系统的初级、次级回路都应进行有效防护,次级回路防护应确保弹体表面可能产生的强静电没有引入全电子安全系统高压回路的潜在通道;初级回路的防护应确保在可信的电/电磁激励下,满足三个开关耐压裕度要求;防护措施应保证耦合到高压电容或雷管上的电压在安全裕度以内。
