基于多谐波联合识别的调频引信定距方法
2022-07-08张玉波
梁 远,黄 岩,张玉波,魏 新
(西安机电信息技术研究所,陕西 西安 710065)
0 引言
连续波调频体制引信是无线电近炸引信的重要组成部分,一般的连续波调频引信采用谐波定距法来确定炸高。传统的谐波定距方法采用基于单次谐波的定距方法,该方法利用回波中的谐波信号与弹目距离之间的对应关系来确定弹目距离[1]。美国的M732A2引信、德国的DM84、瑞典的MK2引信均采用连续波调频体制,通过检测接收信号的不断变化,高频部件向低频放大器输出多普勒信号。当多普勒信号为某一预定数值时,点火电路接通,完成点火和传爆任务[2]。
基于单谐波的定距方法仅关注定距点所对应的单次谐波的信息,所采用的目标识别与抗干扰措施均局限于单次谐波孤立开展,在面对有针对性的干扰时,引信的起爆精度会受到较大影响,甚至失去近炸能力[3]。针对此问题,本文提出基于多次谐波联合识别的调频连续波近炸引信定距方法。
1 基于单谐波的定距方法
调频连续波近炸引信利用同一时刻发射信号与接收信号的频差获取目标的距离信息,由此频差相对于标准频差的偏移量获取目标的速度信息。
调频连续波引信定距公式为:
(1)
式(1)中,n表示谐波阶次,c表示光速,ΔF表示系统带宽。在实际设计中,根据设计要求及预设的系统参数,确定谐波阶次n,即可求出对应的定距高度R。
一般的,为了增强引信系统的可靠性和抗干扰能力,还会选择更高阶次谐波,如第2n次谐波,进行预处理,将其作为判决的必要条件,以打开远端距离门[4]。定距方法原理框图如图1所示。
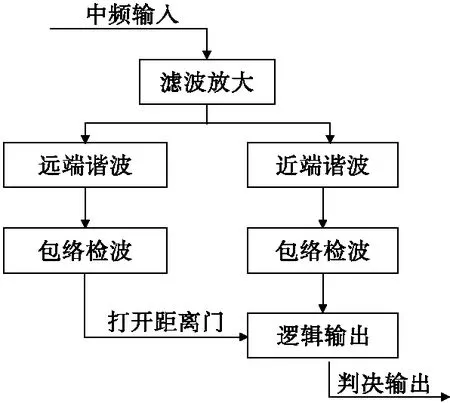
图1 基于单谐波定距方法原理图Fig.1 Principle of ranging method base on single harmonic
2 基于多谐波联合识别的定距方法
基于单谐波的调频连续波引信定距方法只是关注定距点所对应的单次差频谐波的信息,所采用的目标识别与抗干扰措施全部局限于单次谐波孤立开展。基于单谐波信息的处理方法在探测器的灵敏度出现较大差异,或者由于受到干扰而使得接收能量出现变化以及适应起伏的地面目标等情况时具有较大的局限性,其本质在于缺乏信息之间的相互验证性与相互比较性[5]。
本文提出一种调频连续波近炸引信用多谐波联合识别定距方法。该方法在弹目交汇过程中选取多次谐波联合判断,利用多次谐波之间的时间、能量等逻辑关系进行识别。
2.1 基本原理
基于多谐波联合识别的定距方法主要包括两大部分:一是多次谐波的能量信息的识别处理,二是多次谐波的速度信息的识别处理。其基本原理如图2所示。
调频连续波引信的发射信号的数学表达式为:
st(t)=At(t)cos[2πf0t+πmft2+φ0(t0)],
(2)
式(2)中,At(t)为回波信号幅值,mf为调制常数,φ0(t0)为载波初始相位。
回波信号可表示为:
(3)
式(3)中,Δa(t)为寄生调幅,τ=2R/c,代入式(3)可得回波信号的瞬时频率为:
(4)
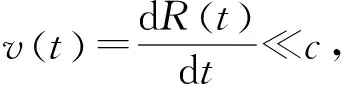
(5)
由式(5)可以看出,回波信号瞬时频率是关于时间的函数,也是关于弹目相对距离R(t)的函数。也就是说回波信号在弹目瞬态交会的过程中携带了目标信息,它既包含有弹目相对运动的多普勒信息,也包含弹目相对运动的距离信息,是时变函数,也是弹目距离的函数[4]。
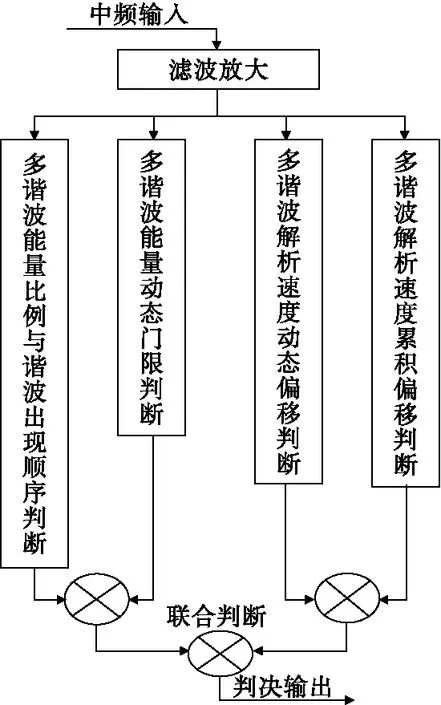
图2 基于多谐波联合识别定距方法原理图Fig.2 Principle of ranging methodbase on multiple harmonics
基于多谐波联合识别定距时,信号处理模块接收宽带中频信号,按照频率由高及低的顺序,将其处理成为等间隔的N次谐波(本文中取N=5),并使其中频率最低的一次谐波所对应的探测距离与要求的定距距离相等;实时地解调出每次谐波包含的目标能量信息和速度信息。
此方法中,根据式(1)选择相应的定距谐波作为上述频率最低谐波,另外四次谐波作为辅助定距信息来源。分别提取五次谐波的能量信息,判定此次交会过程的动态门限,以适应不同探测器灵敏度、不同地面目标散射率。提取五次谐波的出现顺序及速度信息来达到谐波定距的目的,避免对各谐波平滑滤波处理时造成谐波能量包络展宽或距离分辨力降低。
2.2 实现流程
基于多谐波联合识别检测方法具体的实现流程如图3所示。
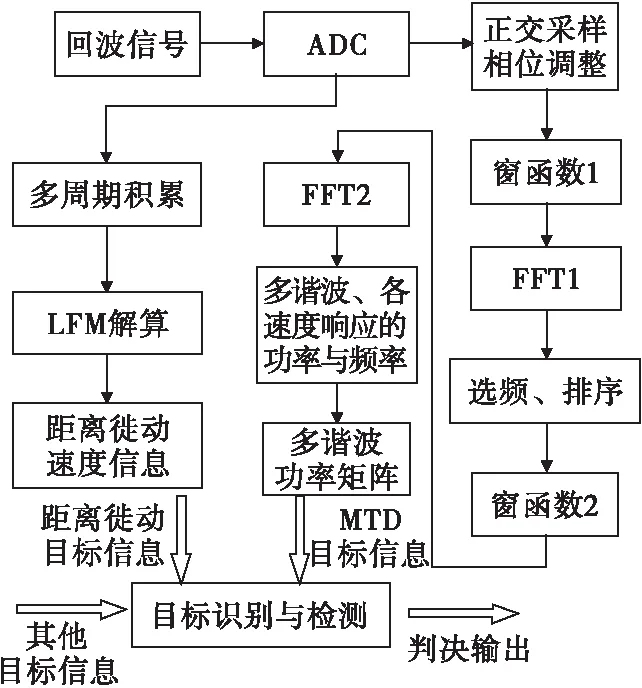
图3 基于多谐波联合识别检测方法流程图Fig.3 Flow chart of ranging methodbase on multiple harmonics
为了保留信号的能量和相位信息,对回波信号进行正交采样。采样数据结合后续的信号处理方法,能够解决零中频相位的正交误差和幅度的不平衡。
假设中频信号的最高频率为fz,带宽为B,中心频率为f0,则ADC的采样率设计为:
(6)
式(6)中,M为正整数。
对对称正负斜率线性调频系统的中频信号采用传统的FFT运算进行脉冲压缩,通过选择合适的窗函数以及合理地设计运算参数,实现频率的高分辨处理[6]。对数字正交采样变换后的信号,按照与探测器同步信号的时延关系进行重新组帧。
延时时间为:
Δt=Δt1+Δt2+Δt3+Δt4,
(7)
式(7)中,Δt1为探测器的系统时延,Δt2为中频滤波放大器的系统时延,为Δt3信号处理器的FPGA片外时延(包括信号整理时延以及ADC的采样时延等),为Δt4数字正交采样的总体处理时延。
重新组帧的同时,还应当根据系统参数截取信号有效区间,完成时域“扣点”的过程。
采用相干脉冲积累的方法对脉冲压缩后同一频率(距离)单元中的信号进行信号叠加,在改善目标回波信噪比的同时,获得目标的多普勒信息,从而最终分别生成各次谐波距离速度二维坐标下的功率矩阵,为后续的目标识别与启动判决提供原始信息。
从加窗的目的角度分析,加窗模块1是为了解决相邻次谐波相互干扰而设;而加窗模块2是为了解决计算信号功率随多普勒频率的变化而起伏的问题。
由于在长时间积累过程中,目标容易发生距离走动,从而限制了传统的相参积累算法的有效积累时间。距离走动通常是由目标快速运动或引信距离分辨率的提高而引起的。在长时间积累过程中,对于速度较低的目标,由于积累时间较长或引信距离分辨率的提高,致使目标可能在多个距离单元间走动;而对于在非长时间积累过程中,目标的高速运动也可能使得目标的回波出现在多个距离单元[7]。严重的距离走动将导致目标回波能量散落在众多距离单元,而使传统相参积累算法无法积累。
在引信弹目交会过程中,可近似认为交会速度恒定,加速度为零,因此仅考虑速度影响,MTD处理结果的时延-多普勒模糊函数可近似表示为[8]:
(8)
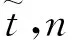
设雷达距离分辨率为ΔR=c/2B,可得高速目标回波包络的跨距离单元数为:
(9)
式(9)表明高速目标会引起回波包络跨越距离单元走动,跨单元数仅与目标速度、积累时间以及信号带宽有关。
去斜后的运动目标中频回波不是单频信号,而是一个LFM信号。其调频斜率与目标的速度及发射信号的调频斜率有关,其中心频率则与参考时延、目标距离、目标速度、调频斜率等因素有关。使用适当的算法对此LFM信号进行参数解调,可获取不依赖于载频以及多普勒信息的弹目速度、高度信息。
经过前期数据处理后得到的MTD目标信息、距离徙动目标信息等,依据一定的规则,在此系统中进行判据综合,从而锁定目标的高度和速度信息,按照预设的条件输出判决信号。
如果此引信探测系统安装在具有弹载导航信息输出功能的武器平台上,则目标识别与检测时还可接收弹载计算机传输的海拔、速度、角度等导航信息,使用这些信息与引信自测信息进行比对拟合,从而提高目标判决的准确性以及抗干扰性能。
3 仿真验证
3.1 模型仿真
在Simulink中对两种方法分别进行仿真。
以载频30 GHz,调制频率300 kHz,定距距离20 m为例,对基于单谐波定距方法进行仿真,结果如图4所示。在弹目交汇过程中,选取两次谐波来进行定距。此方法中,两次谐波独立判决,远端谐波主要用作判断距离门、抗干扰用,近端谐波用来实际定距。
以同样参数对基于多谐波联合识别方法进行仿真。在弹目交汇过程中,接收宽带中频信号,按照频率由高及低的顺序,将其处理成为等间隔的五次谐波,并使其中频率最低的一次谐波所对应的探测距离与要求的定距距离相等,然后实时解调出每次谐波包含的目标能量信息和速度信息。仿真结果如图5所示,图5(a)为多谐波联合识别定距能量图,图5(b)为多谐波联合识别定距速度图。
仿真结果表明,两种方法在理论模型仿真(无噪声等干扰情况下)中,均能够在0.25 s时刻检测到定距谐波,准确定距,并且无明显差异。
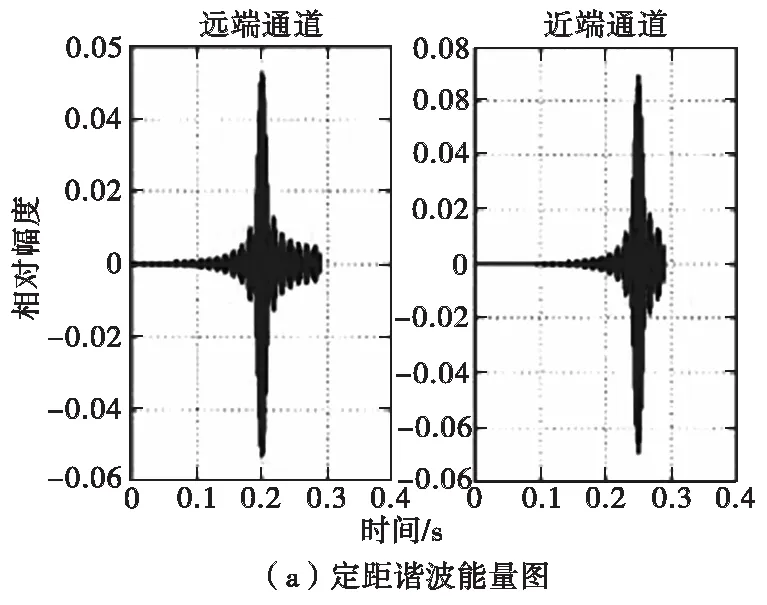
图4 基于单谐波定距仿真图Fig.4 Simulation diagram of ranging method base on single harmonic
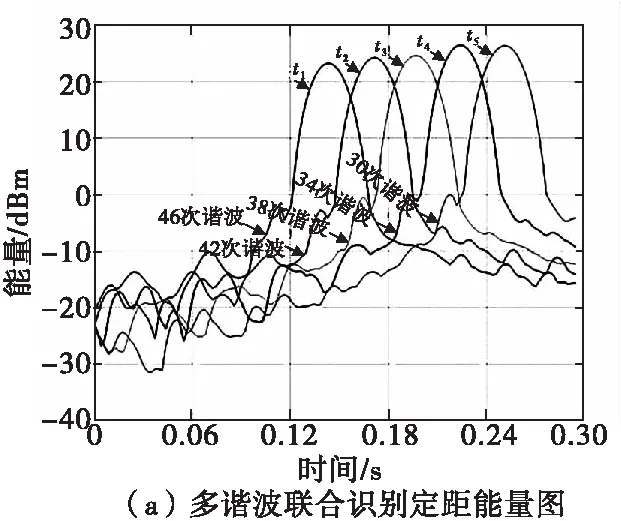
图5 基于多谐波联合识别定距仿真图Fig.5 Simulation diagram of ranging method base on multiple harmonics
3.2 半实物仿真
在实验室内采用半实物仿真来分别验证两种定距方法。系统参数与Simulink仿真时相同。此外,每次半实物仿真试验都设置了同样的有源干扰,干扰模式为扫频-调频干扰。将半实物系统置于空旷场地(前方50 m内无明显障碍物),试验结果如图6、图7所示。
从图6中可以看到,试验中,基于单谐波定距的半实物系统受到干扰,噪声基底抬高,并且检测到了“有效”谐波,并输出了谐波判决信号。图7中,在同样条件下,基于多谐波联合识别定距的半实物系统受到干扰,噪声基底抬高,并没有检测到有效谐波,没有输出谐波判决信号。
对两组试验数据分析,不难发现基于单谐波的定距方法,其用于识别的两次谐波之间缺乏相关性的逻辑比较判断,没有充分利用先验信息,易被相关性较强的干扰信号干扰。基于多谐波联合识别定距方法,在受到干扰时,在能量维度,对于选取的多次谐波之间进行逻辑判断,并与先验信息进行比较,由于多次谐波之间的顺序以及能量关系不满足先验信息,故没有检测到有效谐波;在速度维度,干扰出谐波的时刻,对应时刻的速度值没有收敛至预设区间,故同样没有检测到有效谐波。
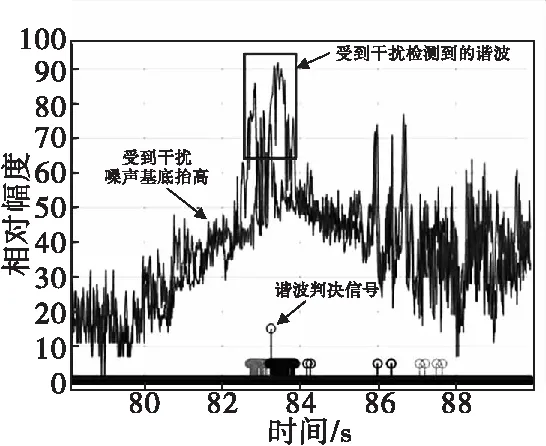
图6 基于单谐波定距半实物仿真Fig.6 Hardware in the loop simulation of ranging method base on single harmonic
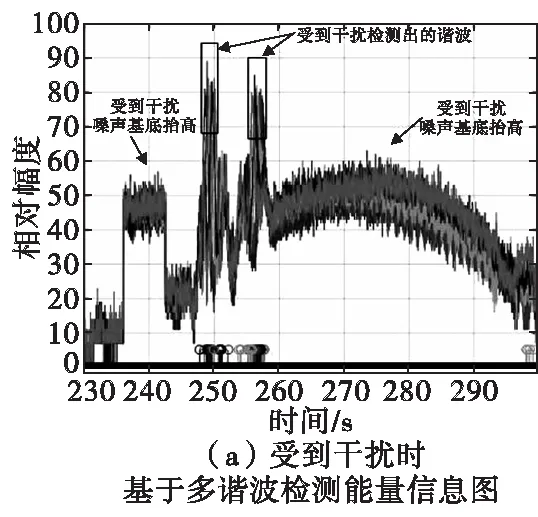
图7 基于多谐波联合识别定距半实物仿真Fig.7 Hardware in the loop simulation of ranging method base on multiple harmonics
对上述两种定距方法进行蒙特卡洛实验。实验一:载频30 GHz,初始相位差0°,调制频率在250~350 kHz之间进行100次蒙特卡罗实验。实验二:载频30 GHz,调制频率为300 kHz,初始相位差在0°~180°之间进行100次蒙特卡罗实验。
实验结果如表1所示。

表1 蒙特卡罗实验结果Tab.1 Monte Carlo test results
表1实验结果表明,相比于单谐波定距基于多谐波联合识别定距方法抗有源干扰能力有较大的提升。
4 结论
本文提出基于多谐波联合识别的调频引信定距方法。该方法利用多谐波的距离信息和速度信息,在多谐波之间进行逻辑上的验证与比较,实现了基于多谐波的联合识别定距。仿真结果表明,基于多谐波联合识别的调频引信定距方法适用于目前的调频连续波近炸引信,并提高引信定距过程中的抗干扰能力。
