矩阵方程AXB+CXD=F的最小二乘解的多步迭代算法

王 杰， 彭振赟， 李 涛

(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

约束矩阵方程

AXB+CXD=F

(1)

是数值代数中研究比较多的一类矩阵方程,在自动控制理论、金融理论、信息论和振动理论等领域具有重要的应用。对矩阵方程(1)应用直接法求解时，通常要求矩阵A、B、C及D能够同时相似于某种标准形；将矩阵方程(1)转化为线性方程组迭代求解时，迭代矩阵的阶数为原矩阵阶数的平方，除了计算量较大之外，其收敛性问题也较复杂。因此，求解矩阵方程(1)的主要方法是迭代算法。李海合等[1]和张凯院等[2]通过引入参数提出了一种求解矩阵方程(1)的不动点迭代算法。Ding等[3]基于求解线性方程组的雅可比迭代算法和高斯-塞德尔迭代算法思想提出了一种求解矩阵方程(1)的不动点迭代算法。当未知矩阵X具有结构约束条件时，求解矩阵方程(1)的方法主要是共轭梯度算法，如刘大瑾等[4]讨论了中心对称解及其最佳逼近解的求解，周海林[5]讨论了广义双对称解的求解，尚丽娜等[6]讨论了中心对称最小二乘解，孙合明等[7]讨论了自反和反自反解及其最佳逼近解的求解，Liu[8]讨论了广义中心对称解及其最优逼近解的求解，Yuan等[9]讨论了最小二乘Hermitian解及其最小二乘Hermitian解的求解，闫熙等[10]讨论了唯一解的参数迭代方法，并给出了最优参数的确定方法。鉴于此，讨论矩阵方程(1)及其最小二乘解的求解问题，即考虑如下2个问题：

问题1给定矩阵A、C∈Rm×n,B、D∈Rn×p和F∈Rm×p，求X∈Rn×n，使得

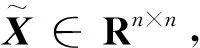
其中：‖A‖F为矩阵A的Frobenius范数；SE为问题1的解集合。

提出了一种求解问题1的多步迭代算法，证明了由多步迭代算法产生的矩阵序列收敛于问题1矩阵方程的最小Frobenius范数解，通过修改系数矩阵F，证明了由多步迭代算法产生的矩阵序列收敛于问题2的解，同时给出了提出的多步迭代算法与不动点算法和共轭梯度算法的数值比较。

1 求解问题1和问题2的多步迭代算法

显然，问题1的法方程为

AT(AXB+CXD)BT+CT(AXB+CXD)DT=

ATFBT+CTFDT,

(2)

因此，求解问题1等价于求解矩阵方程(2)，且矩阵方程(2)一定有解。利用共轭梯度算法求解矩阵方程(2)时，其完整的迭代格式如下：

算法1共轭梯度算法求解问题1

1) 输入A、B、C、D、F，初始矩阵X0∈Rn×n，令k=0;

2) 计算

R0=AT(F-AX0B-CX0D)BT+

CT(F-AX0B-CX0D)DT,

P0=AT(AR0B+CR0D)BT+

CT(AR0B+CR0D)DT;

3) 若‖Rk‖F<ε,则停止，否则，k=k+1；

4) 计算

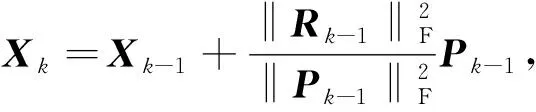
5) 返回步骤3)。

算法2不动点迭代算法求解问题1

1) 输入A、B、C、D、F，初始矩阵X0∈Rn×n，误差精度ε>0，令k=0；

2) 计算

Xk+1=Xk-μ[AT(AXkB+CXkD-F)BT+

CT(AXkB+CXkD-F)DT],

Rk+1=AT(AXk+1B+CXk+1D-F)BT+

CT(AXk+1B+CXk+1D-F)DT,

其中,

0<μ<

λmax(A)为矩阵A的最大特征值;

3) 若‖Rk+1‖F<ε，则停止，否则，令k=k+1，转步骤2)。

令

(3)

算法3求解问题1的多步迭代算法

1) 输入矩阵A、B、C、D、F，整数m>0，误差精度ε>0，取初始矩阵X0∈Rn×n；

2) 计算f(X0)=g(X0)-X0，令k=0；

3) 若‖f(Xk)‖F<ε，则停止，此时Xk为问题1的解；

4) 令mk=min(m,k)；

5) 计算γk=(γ1,γ2,…,γmk-1)T∈Rmk-1，使

(4)

其中，‖x‖2为向量x的2-范数；

6) 令

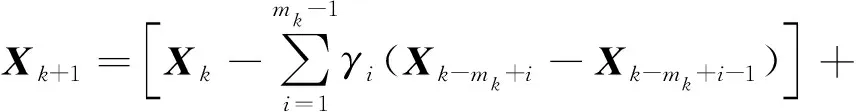
(5)

7) 令k=k+1，转步骤3)。

为了证明多步迭代算法3的收敛性，先证明如下引理。

引理1若y0为线性方程My=b及其最小二乘问题的解，且y0∈R(MT)，则y0为线性方程组My=b及其最小二乘问题的最小Frobenius范数解。

证明将M奇异值分解为

则U=(U1,U2)和V=(V1,V2)为正交矩阵，那么矩阵A的Moore-Penrose广义逆为

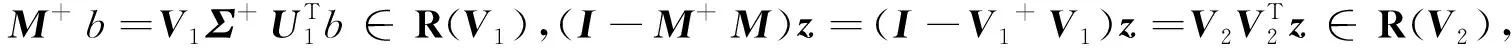
矩阵方程AXB+CXD=F等价于线性方程组(BT⊗A+DT⊗C)vec(X)=vec(F)，其中，A⊗B表示矩阵A和B的Kronecker积，vec(A)表示矩阵A的拉直算子，由引理1易证引理2成立。

引理2若X矩阵方程AXB+CXD=F的解，且vec(X)∈R(B⊗AT+D⊗CT)，则X是矩阵方程AXB+CXD=F及其最小二乘问题的最小Frobenius范数解。

定理1对任意初始矩阵X0∈Rn×n，由算法3所产生的矩阵序列{Xk}收敛于问题1的解。进一步地，若任意初始矩阵X0=ATHBT+CTHDT，H∈Rm×p为任意矩阵，则由算法3所产生的矩阵序列{Xk}收敛于问题1的最小Frobenius范数解。

证明由式(3)和(5)可知，

f(Xk+1)=g(Xk+1)-Xk+1=-μ[AT(AXk+1B+

CXk+1D-F)BT+CT(AXk+1B+CXk+1D-F)DT]=

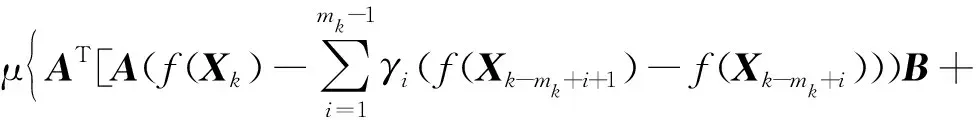
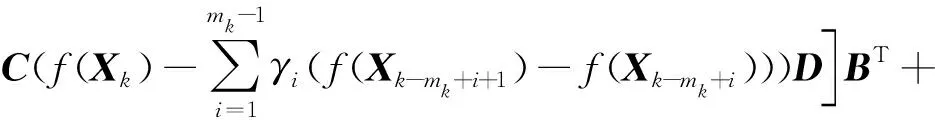
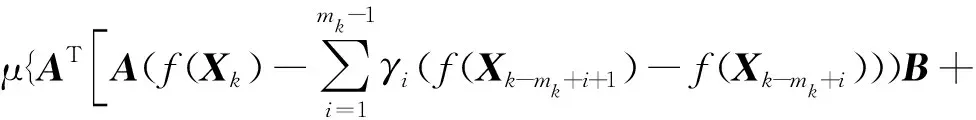
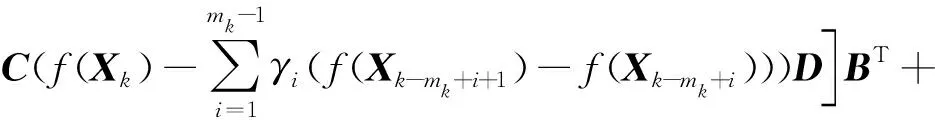
μ(BBT⊗ATA+CCT⊗DTD){f(Xk)-

因而，有

vec[f(Xk+1)]=[I-μ(BBT⊗ATA+CCT⊗DTD)]

进而有

‖f(Xk+1)‖F≤‖I-μ(BBT⊗ATA+CCT⊗DTD)‖2·

其中，‖A‖2为矩阵A的谱范数。γk=(γ1,γ2,…,γmk)∈Rmk-1为最小二乘问题(4)的解, 因而有

‖f(Xk)‖F,

由于

0<μ<

则有

c=‖I-μ(BBT⊗ATA+CCT⊗DTD)‖2<1，

因此，有

‖f(Xk+1)‖F≤c‖f(Xk)‖F≤…≤ck+1‖f(X0)‖F，

故可得

‖f(Xk+1)‖F→0,k→∞。

因此，算法3所产生的矩阵序列{Xk}收敛于问题Ⅰ的解。

进一步地，若X0=ATHBT+CTHDT，H∈Rm×p为任意矩阵，则有vec(X0)∈R(B⊗AT+D⊗CT)。由算法3可知，对于任意的k都有vec(Xk)∈R(B⊗AT+D⊗CT)，因此，由引理2可知，算法3所产生的矩阵序列{Xk}收敛于问题1的最小Frobenius范数解。

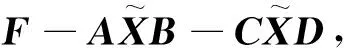
证明显然，式(2)等价于矩阵方程：

(6)

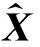
命题成立。

2 数值实验

所有数据均通过MATLAB R2016a，Windows 7 64 bit Intel®CoreTMi5-6500处理器、3.20 GHz的PC获得。算法1～3中的误差精度均固定为ε=10-7，初始矩阵选取适当阶数的零矩阵，算法2、3中的参数μ选取

多步迭代算法3中m=10，共轭梯度算法、不动点迭代算法和多步迭代算法的最大迭代次数限制为Imax=50 000。已知矩阵A、B、C、D、F和X0以MATLAB格式给出：

A=randn(m,n),B=randn(n,p),

C=randn(m,n),D=randn(n,p),

F=randn(m,p),X0=randn(n,n),

则得到共轭梯度算法、不动点迭代算法和多步迭代算法的10次试验的平均值如表1所示，其中IT为算法迭代次数，CPU为算法求解所用的时间。

表1 共轭梯度算法、不动点迭代算法和多步迭代算法的数值比较

由表1数据及其他实验数据可得以下结论：

1)当初始矩阵A、B、C、D、F为方阵，即m=n时,共轭梯度算法和多步迭代算法的收敛效果明显优于不动点迭代算法。

2)当初始矩阵为长方形矩阵,即m≠n≠p，多步迭代算法有较为明显的优势，相比共轭梯度算法和不动点迭代算法，不仅迭代次数大大减少，收敛速度也大幅加快。总的来说，多步迭代算法通过加速，明显优于共轭梯度算法和不动点迭代算法。

3 结束语

通过对矩阵方程AXB+CXD=F及其最小二乘问题的研究，提出了一种多步迭代算法，用以求解矩阵方程的最小二乘解，此算法通过前mk步的线性组合求解下一步的解，不仅得到的结果更加精确，而且极大地减少了迭代次数，加快了收敛速度。该算法应用到其他类型矩阵方程的收敛效果，以及如何选取最优收敛因子μ和向量数mk使多步迭代算法达到最好的收敛效果，还有待进一步研究。