基于约束采样RRT的机械臂运动规划
2022-07-07李新宇董昊臻
张 振,李新宇,董昊臻,周 林,高 亮+
(1.华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074; 2.航天科工智能运筹与信息安全研究院(武汉)有限公司 体系设计中心,湖北 武汉 430040)
0 引言
工业机器人广泛应用于汽车、航空、船舶等工业生产领域[1]。随着机器人化智能制造的提出和发展,传统示教编程的方式无法满足作业场景日渐增加的生产需求,因此应用稳定快速的运动规划算法使机器人自主规划运动轨迹,进行高效、灵活地作业,成为当前的研究热点,国内外学者对此展开了大量研究[2]。
根据环境建模方法和搜索策略的不同,机器人运动规划分为图搜索算法[3-6]和基于随机采样的规划方法两类。在复杂环境和高维空间下,图搜索算法难以对障碍物进行建模和描述,而基于随机采样的概率路线图(Probabilistic Road Map,PRM)[7]和快速搜索随机树(Rapidly-exploring Random Tree,RRT)[8]能较好地解决这一问题。相比前者,RRT算法采用单查询、增量式扩展方法,无需构建路线图[9],然而传统RRT算法在搜索过程中存在规划效率低[10]、导向性较差、路径平滑较差等问题,近年来学者们针对机械臂具体应用场景和性能要求,不断改进RRT算法,力求解决以上问题。
KALISIAK等[11]提出RRT-blossom算法,利用回归约束函数产生新节点,降低随机树重复区域的搜索概率,但限制了节点的自适应拓展,路径平均长度较长;为解决上述问题,KARAMAN等[12]提出渐进最优RRT(RRT*)算法,通过重选父节点及布线迭代找到最优路径,但其搜索效率较低;GAMMELL等[13]提出Informed RRT*算法,通过限制搜索区域更快地接近最优解,但无法限制随机树的规模;MASHAYEKHI等[14]在RRT*中引入双树拓展策略,通过同时扩展两树来提高搜索速度并不断优化路径;针对RRT获得的路径质量差和探索存在盲目性的问题,PALMIERI等[15]提出Theta*-RRT算法,该算法速度更快、路径质量更优,但存在重复搜索的问题;ZHANG等[16]引入回归机制和自适应扩展机制,防止对配置空间过度搜索;LIU等[17]将目标引力变量加入RRT,获得不同长度的步长以提高搜索效率,但易使搜索陷入局部最小值。
基于上述成果,针对RRT算法拓展效率低、收敛速度慢和路径粗糙的问题,本文提出一种基于约束采样的RRT算法。通过舍弃已探索区域的采样点来减少冗余节点,使随机树朝向未探索区域生长,并采用动态采样域和贪婪策略提高收敛速度,剔除路径的冗余节点来缩短路径长度,然后结合三次B样条曲线来平滑轨迹。最后通过MATLAB和机器人操作系统(Robot Operating System, ROS)平台分别进行仿真和真机实验,验证该算法有效可行。
1 改进的快速搜索随机树算法
1.1 快速搜索随机树算法基本原理
RRT是一种基于随机采样的路径探索方法[18]。首先,算法以路径起点xinit作为随机树T的根节点,通过随机采样得到采样点xrand;然后,在已有随机树中找到距离xrand最近的节点xnear;从xnear指向xrand的方向上,以一定步长生长得到新节点xnew,若拓展到xnew的路径上没有碰到障碍物,则将xnew节点加入随机搜索树,否则重新进行采样和随机树生长;随着迭代次数的增加,当随机树上新添加的叶子节点xnew等于目标点xgoal时,搜索完成,找到一条自xinit到xgoal的可行路径。
通过分析随机树的生长过程可知,RRT算法倾向于拓展到开阔的未探索空间。设随机树的已探索空间在整个探索空间占比为P,表示为
(1)
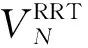
图1所示为RRT生长过程。可见,当迭代次数较少时,用随机采样不会影响随机树探索未拓展空间的效率;随着迭代次数的增加,未拓展区域减少,在已探索过的区域内仍会产生xrand,导致大量的重复生长。在该过程中,遍历随机树节点找寻xnear并进行碰撞检测占用了大量计算资源,对于已探索过的区域,这样的消耗是不必要的。
标准RRT将固定空间作为采样域,意味着每次产生采样点xrand的空间是相同的,无指向性的随机采样具有探索未拓展空间的倾向,但在简单地图中搜寻可以到达xgoal的可行路径时,这种采样方式缺乏引导,会随机向各个方向拓展,生成大量无用节点,收敛速度慢。
PPT规划出的路径花费较长且弯折多,直接使用会使机械臂在运行中产生速度、加速度突变,造成机械臂振动,因此需要对规划路径进行优化才能应用于机械臂避障任务。
1.2 稀疏节点产生机制
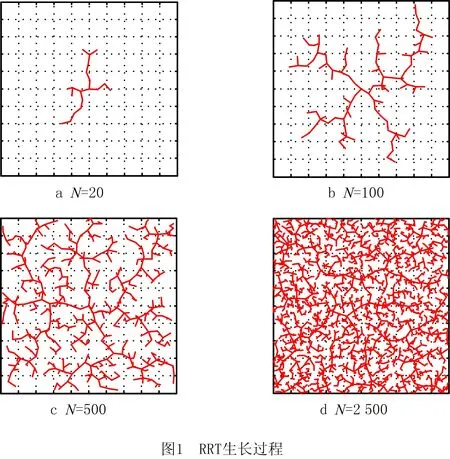
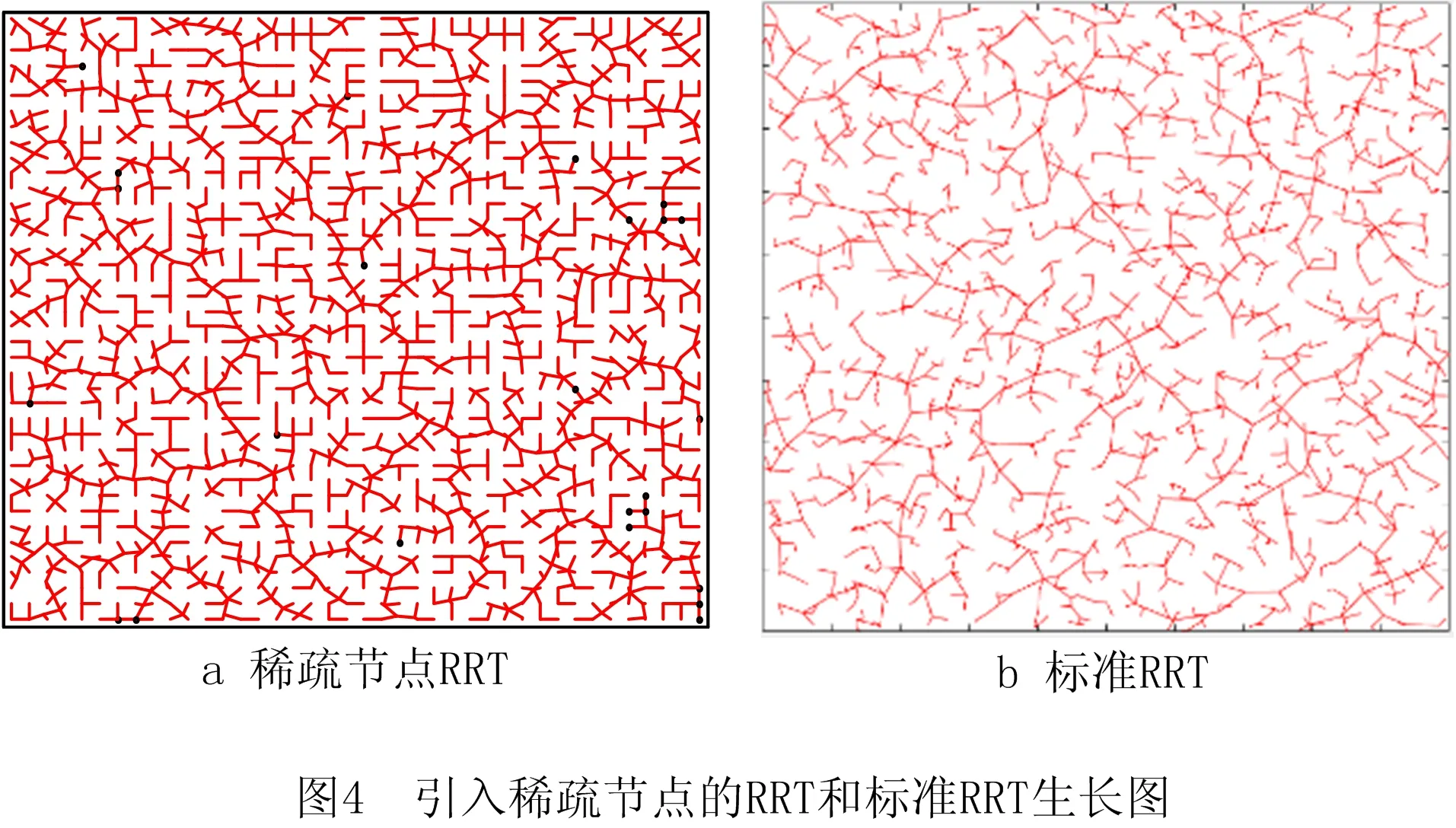
为减少标准RRT算法对已探索区域的重复搜索,本文提出一种稀疏节点产生机制,该机制产生稀疏节点的流程图如图2所示。稀疏节点的生长过程如图3所示,假设探索空间被划分为6×5个独立方格,h为单位方格长度,称每个单位方格为一个域。
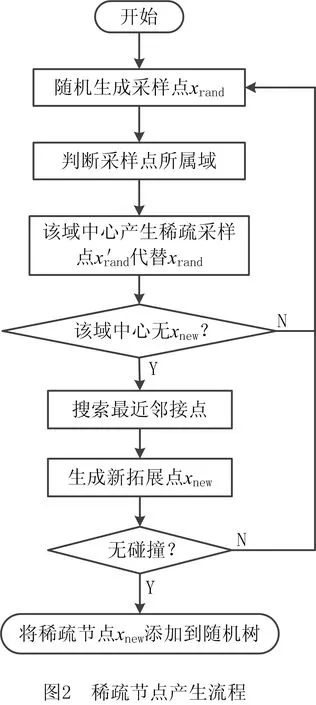
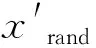
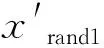
标准RRT在整个自由空间中采样,因此xgoal与树中最接近它的叶子节点之间的距离终将收敛到0。因此无论ε有多小,最终总会有新的叶子节点xnew满足条件
|xnew-xgoal|<ε。
(2)
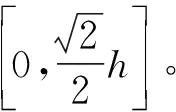
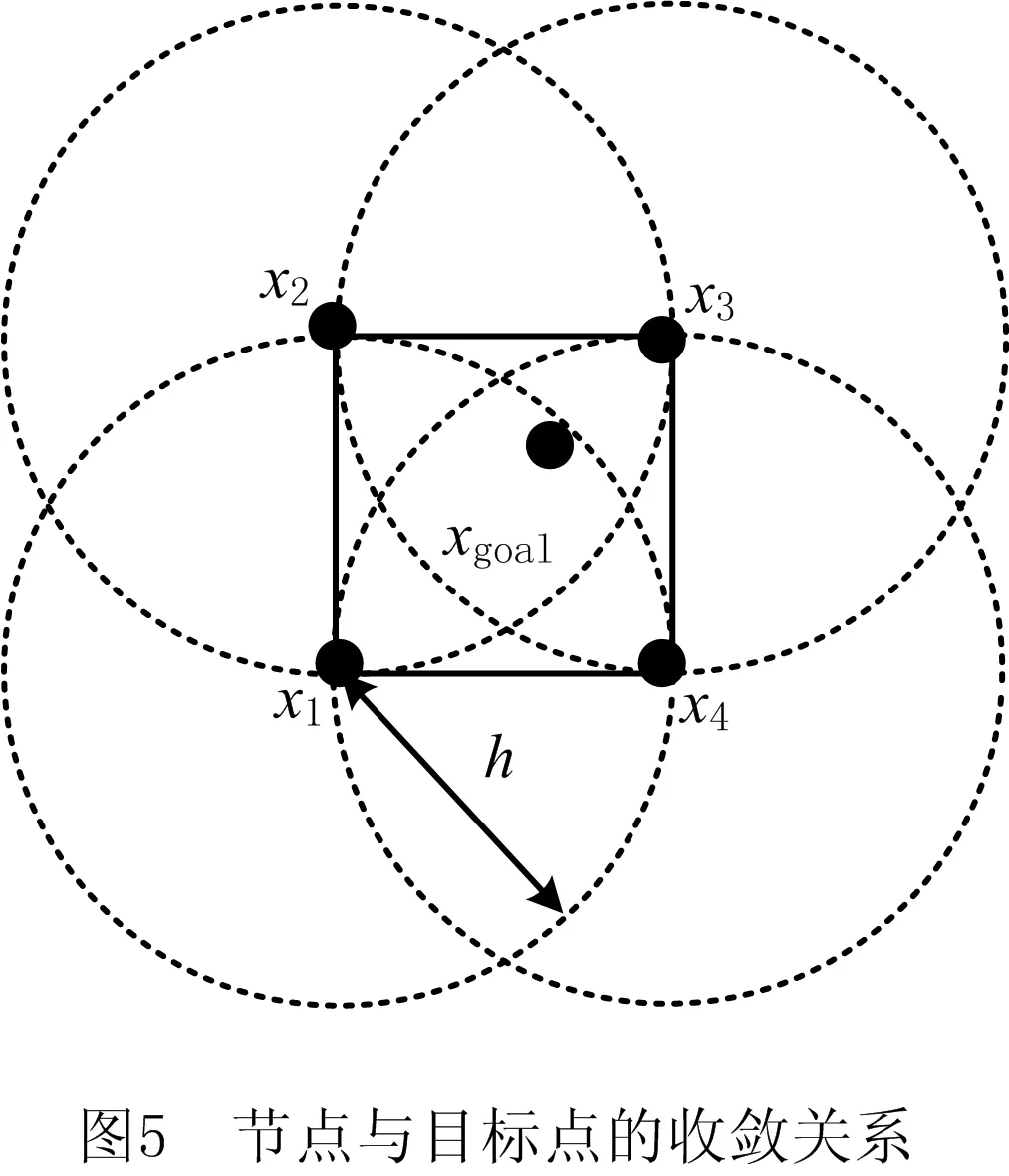
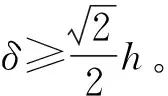
|xgoal-xnew|≤d;
OBS_NOT_FREE(xgoal,xnew)。
(3)
函数Create_Sparse_Node(T,h,u,NumOfNode)为本文所提稀疏节点生成机制,伪代码描述如下:
函数1Create_Sparse_Node(T,h,u,NumOfNode)。
1.xrand←RANDOM();
3.for i=1:NumOfNode
5. return xrand;
6. end if
7. i=i+1
8.end for
11.if OBS_ FREE(xnear,xnew)
12.T←T.add_vertex(xnew);
13.end if
1.3 动态采样域策略
在标准RRT算法中,随机树因扩展方向随机性过强而在开阔区域进行大量无用搜索,为加快算法收敛速度,通常将引力函数加入RRT算法,引导随机树向目标点方向生长,但当目标点被障碍物阻挡时,随机树拓展将陷入局部最小值。一个良好的采样策略不仅应具有全局性的特点,还要有局部差异性,本文提出一种动态变化的采样域策略,使生成的采样点在以目标点为圆心、goal_r为半径的圆内,
(4)
式中:L为探索区域边界的长度;V为控制goal_r半径变化的权值,
(5)
式中:N1为能够生成叶子节点的采样点数量;N2为未通过碰撞检测的采样点数量;λ决定权值变化的快慢。当N1>N2时采样半径缩小,反之采样半径增大,但采样范围不应超出探索空间的边界。若权值V较大,则说明探索空间开阔,采样范围缩小到目标点附近,从而减少随机树在开阔空间生长的盲目性,加快随机树向目标点收敛的速度;若探索空间有障碍阻挡,则N2增大使权值V减小,从而扩大以目标点为圆心的采样半径,使随机树跳出局部极小值。
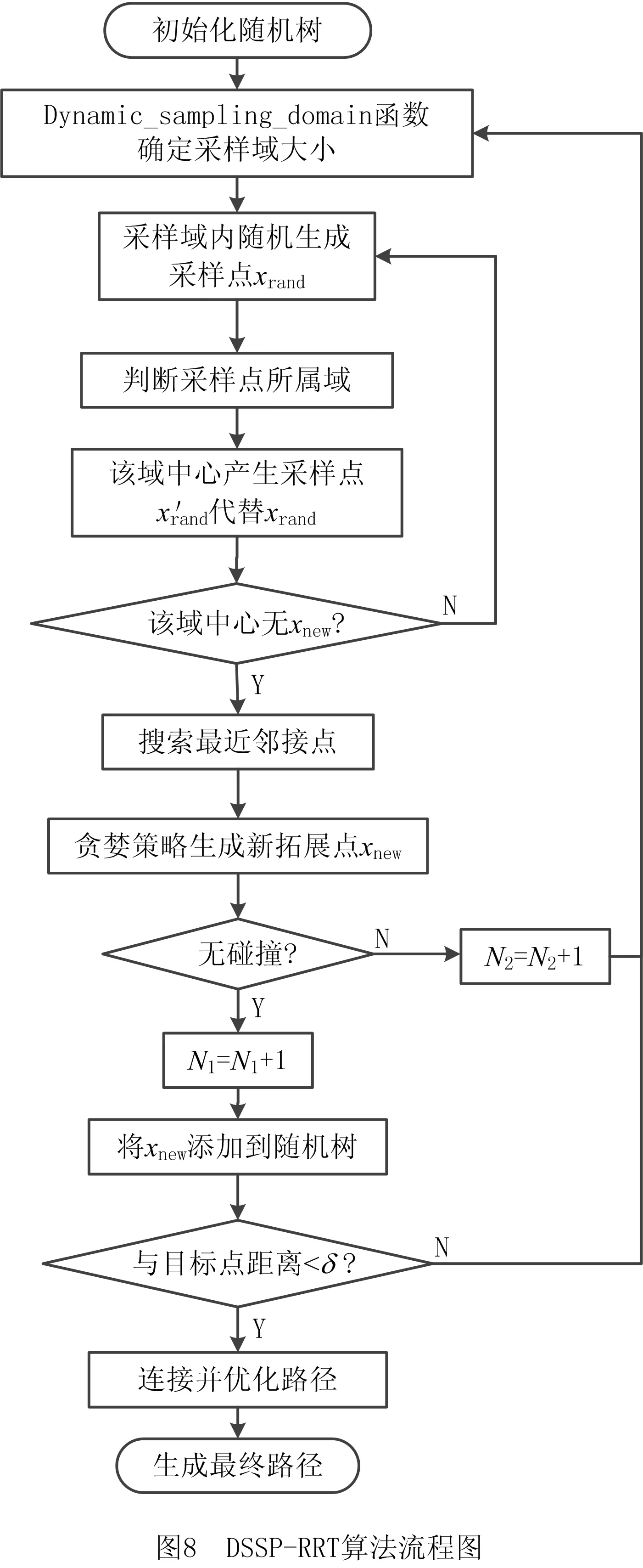
采用遗忘式采样点计数方法生成S个采样点后,将权值V初始化,以及时反映随机树拓展边界附近障碍物的分布情况,提高本策略的鲁棒性。函数Dynamic_sampling_domain(N1,N2,S,M,L)即为动态采样域策略,其伪代码描述如下:
函数2Dynamic_sampling_domain(N1,N2,S,M,L)。
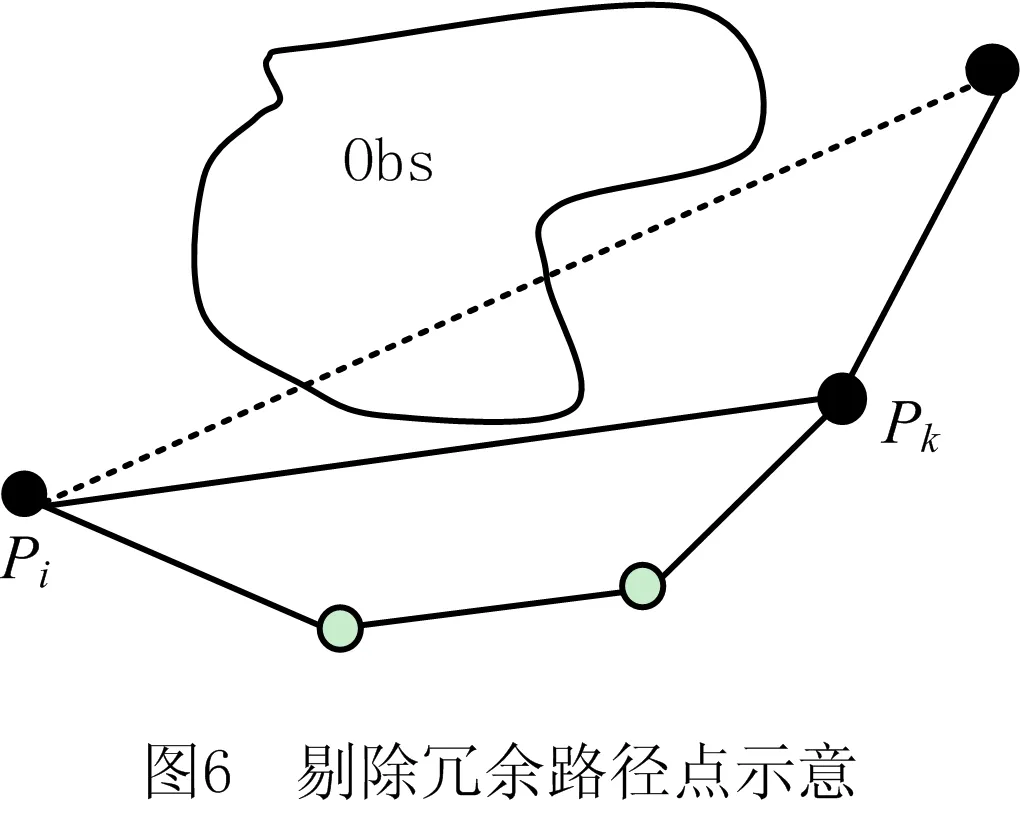
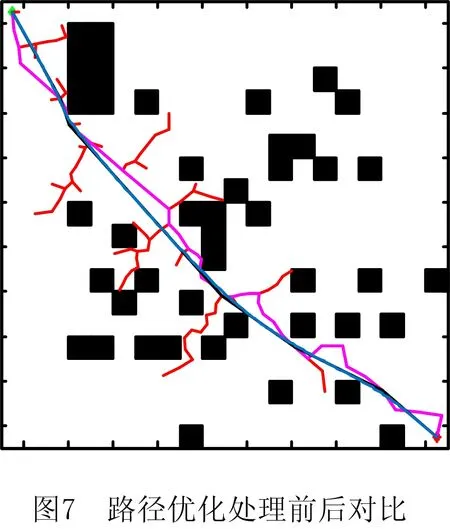
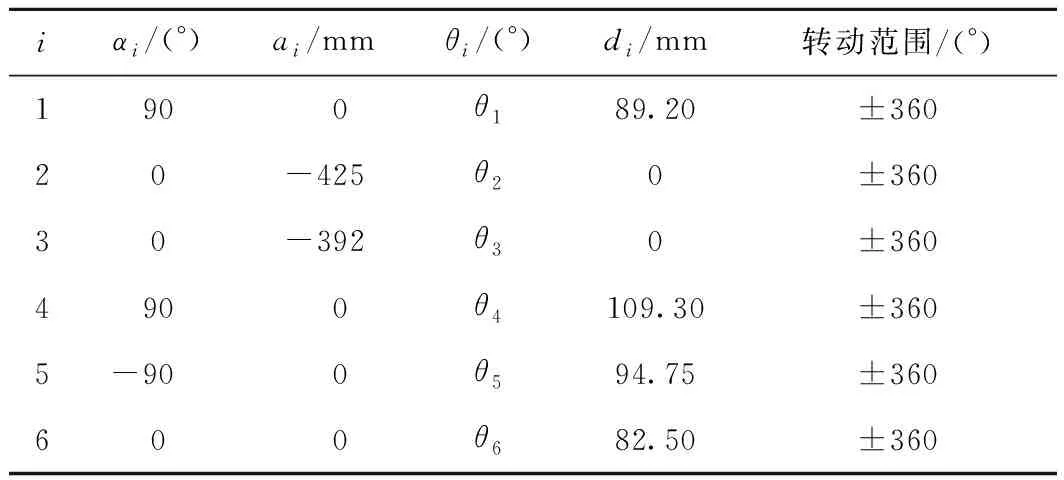
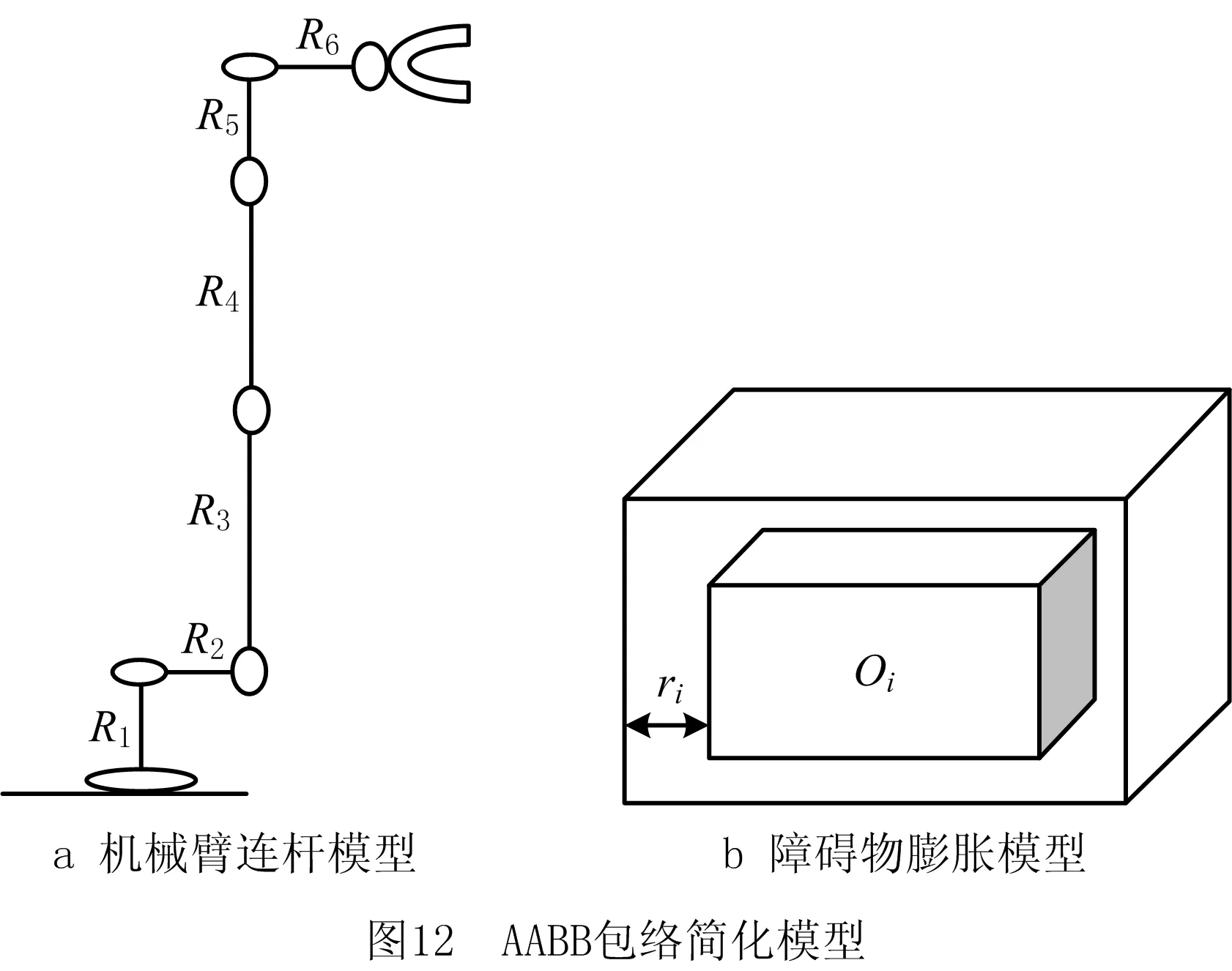
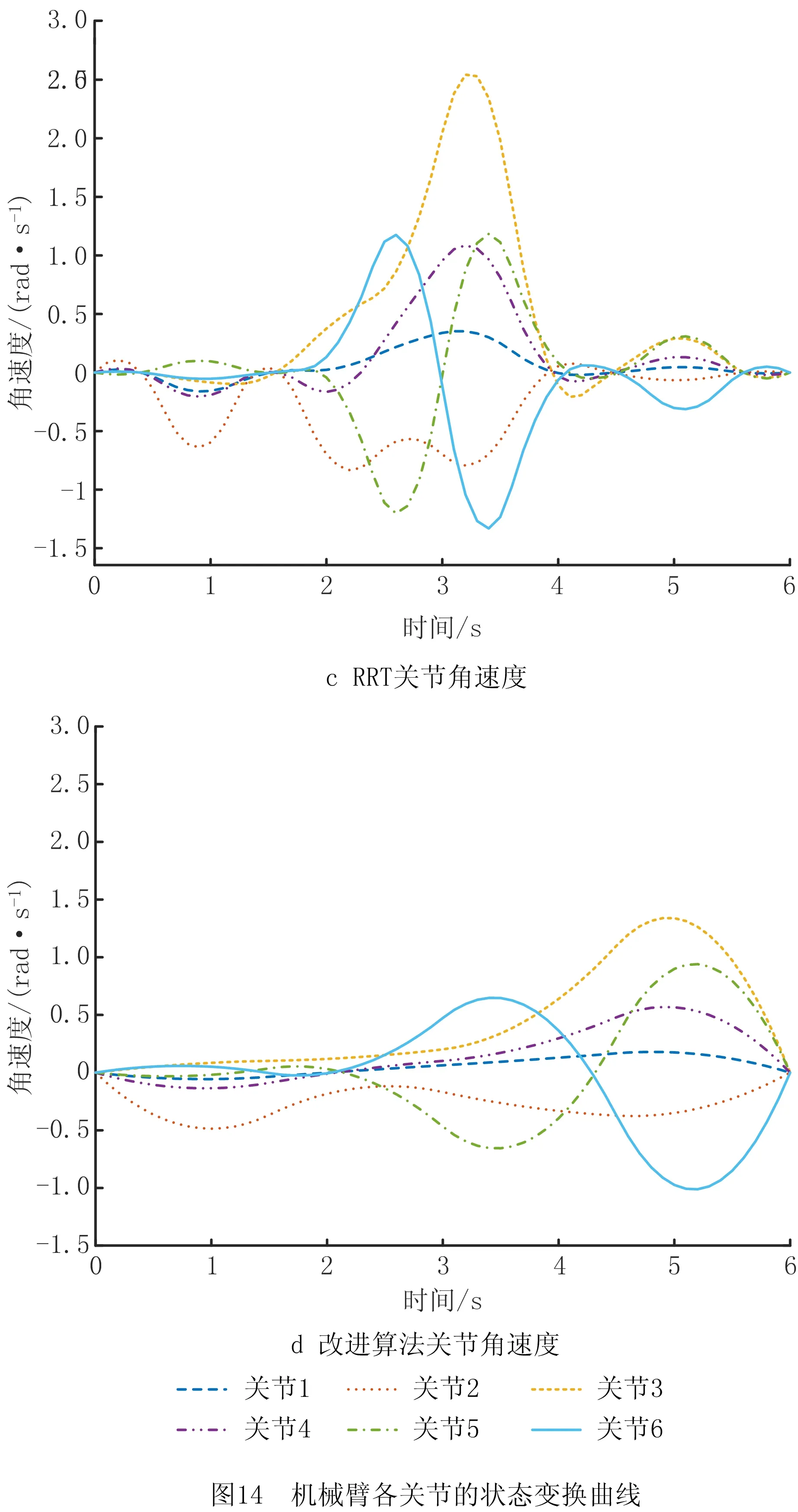
1.if N1+N2 2. V=(N1/N2)^λ; 3. if V>M 4. goal_r=L/V; 5. if goal_r>L 6. goal_r=L; 7. end if 8. else 9. goal_r=L; 10. end if 11.end if L=V×u。 (6) 贪婪策略能够以大步长产生新拓展点,从而减少空白区域的无用搜索,提高局部收敛速度。 假设采用DSSP-RRT算法规划所得路径节点为P[P1,P2,P3,…,Pn],如图6所示,若节点Pi与Pk之间的直线路径无碰撞,则Pi与Pk间的节点均为冗余节点,将其从路径节点序列中剔除。从起点开始,遍历整个路径节点序列,去除所有冗余节点,所得路径长度较短且曲率小、弯折少。 准均匀B样条曲线可对弯折处的局部路径进行平滑处理,且不对整条路径的基本形状造成影响[19],故本文采用三次B样条曲线对算法所规划的路径进行平滑处理。 三次B样条基函数为: (7) 三次B样条曲线段 c0,3(u)=c0×N0,3(u)+c1×N1,3(u)+ c2×N2,3(u)+c3×N3,3(u)。 (8) 当给定控制点后,可利用式(8)求出一系列满足三次B样条的曲线点。 如图7所示,以DSSP-RRT算法为例,在一个存在随机障碍物的环境中,左上角为起点,右下角为目标点,生成随机树,树的主干线条为初步规划所得路径,应用上文所述方法除去冗余节点,得到弯折的较短路径,经过B样条平滑处理后得到最终路径。可见,优化后的路径较短且平滑,基本保持原有形状走势。 DSSP-RRT算法的详细过程如图8所示。改进算法能够减少对已探索区域的重复探索,提高采样点的目标导向性,加快随机树的收敛速度,减少路径弯折,缩短路径长度。 为验证改进算法DSSP-RRT的性能优势,设计两种不同复杂度的场景进行仿真对比,实验将标准RRT,PB-RRT,GB-RRT和本文提出的DSSP-RRT进行对比,4种算法中对应的参数相同。其中GB-RRT步长u1=16,u2=8,其余实验算法步长u=20。PB-RRT算法的概率值P=0.8,DSSP-RRT算法的域长度h=10,权值V中的幂值λ=3,M=3,S=300。 两个仿真地图分别为障碍散乱分布场景和迷宫场景,大小均为400×400,起始点为(20,20),目标点为(380,380)。如图9和图10所示,场景中设有四边形随机障碍物,随机树的主干线段为规划路径。表1和表2所示为4种算法在到达目标点过程中的搜索时间、所产生节点数量和路径长度的对比。 表1 散乱障碍环境中4种算法的实验结果 表2 迷宫环境中4种算法的实验结果 仿真实验在MATLAB R2021b软件中进行,计算机配置为64位Windows 10操作系统、Intel Core i7-8750H处理器。为保证仿真的真实有效性,各场景地图均进行20次重复实验,并取数据平均值作为结果。 由表1可知,在障碍物散乱分布的场景中,GB-RRT算法和PB-RRT算法的表现明显优于标准RRT,而DSSP-RRT在搜索时间和迭代次数上比RRT算法分别减少88%和94%,路径长度减少10%,其各项指标均优于GB-RRT算法和PB-RRT算法。这是因为引入的动态采样域策略,通过将拓展成功的采样点与未通过碰撞检测的采样点数量之比的动态变化作为权值影响采样域的范围,使散乱障碍物环境中的采样范围迅速收缩到目标点附近,减少了随机树在开阔空间盲目生长所产生的节点数,同时贪婪策略的引入进一步减少了拓展中无用节点的数量。两种策略大大减少了算法无效迭代浪费的时间,加快了算法的收敛速度。 由表2可知,在迷宫环境中,GB-RRT算法和PB-RRT算法比标准RRT表现差,而DSSP-RRT算法的搜索时间、迭代次数、路径长度比RRT算法分别减少79%,78%,7%。这是因为GB-RRT算法和PB-RRT算法在狭窄通道或局部受限区域中搜索时易陷入局部最小,标准RRT算法在已探索区域重复采样搜索产生大量步长极短的拓展点,导致大量计算资源浪费在寻找xnear和碰撞检测上。而DSSP-RRT算法引入的稀疏节点产生机制仅保留未探索区域的稀疏采样,减少了已搜索区域的重复采样,从而减少遍历随机树节点寻找最近节点的次数,进而减少产生新节点时碰撞检测的次数,保证复杂环境中的随机树稀疏而整齐。 在两个地图中,DSSP-RRT算法相比RRT算法在路径长度上分别减少10%和7%,且均优于GB-RRT算法和PB-RRT算法,这是由于引入去除路径中冗余节点的路径处理方法和B样条曲线的平滑方法而获得了较优路径。 本文研究对象为UR5串联机械臂,其D-H坐标如图11所示,相关D-H参数如表3所示。 表3 机械臂D-H参数 根据D-H模型及参数,可得该机械臂相邻两关节之间的齐次变换矩阵 (9) 式中:cθi表示cosθi,sθi表示sinθi。末端坐标系到基坐标系的变换矩阵 (10) 式中:n,o,a3个列向量表示机械臂的姿态;px,py,pz表示末端执行器坐标系原点在世界坐标系中的位置。 碰撞检测在运动规划过程中所用时间的占比达90%[20],因此选取合适的碰撞检测方法可有效提高规划效率。本文根据机械臂结构形态和障碍物几何形状选用轴向平行包围盒(Aixe Align Bounding Box, AABB)包络法。AABB包络法指用最小体积的六面体将机械臂各连杆和障碍物分别进行包络[21],使机械臂与障碍物间的碰撞检测问题转化为对空间平面之间位置关系的判断[22]。为进一步简化,以机械臂连杆的径向最大半径ri对障碍物进行膨胀处理,从而将判断空间平面间的碰撞转化为判断空间直线与平面间的位置关系。如图12所示,包络UR5机械臂各连杆的空间线段方程为{R1,R2,…,R6},包络障碍物的六面体为Oi。若{R1,R2,…,R6}与Oi各面存在交点,则机械臂与障碍物发生碰撞,需重新规划路径,否则机械臂按搜索轨迹运动。 为验证本文所提DSSP-RRT算法有效可行,在MATLAB 2021b版本Robotic System Toolbox工具箱搭建UR5机械臂仿真场景并进行运动规划实验。在关节空间采样规划,采用正运动学在Work-Space进行碰撞检测,将初步规划的无碰撞路径用回溯去除冗余节点策略进行剪枝,然后采用三次B样条曲线得到最终的平滑轨迹。 图13所示为DSSP-RRT算法与标准RRT算法应用于UR5机械臂避障运动规划的末端轨迹对比效果。机械臂由初始姿态(单位:rad)(1.016,-0.339,-1.712,0.158,2.066,-0.570 9),避开长0.6 m、宽0.03 m、高0.35 m的长方体障碍物及3个圆柱体障碍物到达目标姿态(1.342,-1.987,0.893,1.041,2.296,-0.852)。路点组成的线段为末端轨迹,从图中可见RRT算法规划的轨迹点散乱,DSSP-RRT算法规划的轨迹较平滑且能够成功避障。 图14所示为机械臂各关节角度及角速度变化曲线,可见DSSP-RRT算法由于剔除了冗余路径点,有效减小了关节角度极值;而且由于结合B样条曲线得到平滑的关节轨迹,降低了角速度变换范围,减少了机械臂关节抖振情况,从而保证机械臂平稳避障。两种算法的实验结果如表4所示,可见DSSP-RRT算法以产生稀疏节点的机制和变化的采样域进行采样,提高了节点利用率和收敛速度,使节点数量减少76.19%,进而使时间成本降低74.81%,有效提高了轨迹规划效率。 表4 算法实验结果对比 为进一步验证本文所提DSSP-RRT算法应用于机械臂运动规划的实用性,在ROS平台下的MoveIt!搭建UR5机械臂障碍场景并进行运动规划测试。将DSSP-RRT算法开发成规划器编写进OMPL(open motion planning library)库并作为插件与MoveIt!交互,在关节空间中采用标准RRT算法和DSSP-RRT算法进行采样规划,结合MoveIt!自有运动学求解器,对机械臂各个采样位姿进行碰撞检测,进而规划出运动轨迹。 如图15所示,在Rviz可视化场景中,带隔板桌面为障碍物,深色不透明机械臂为始末位姿,半透明机械臂为按所规划路径运动过程中的位姿变化。可见机械臂采用DSSP-RRT算法能够顺利避障并到达目标位姿。 图16所示为真实环境下的UR5机械臂运动规划验证实验。采用Intel RealSense Depth Camera D435i相机获取障碍环境信息,白色长方体为障碍物,机械臂自左侧起始位姿规划出了一条到达右侧目标位姿的无碰撞路径,能够在真实环境中有效完成避障任务,证明了本文所提算法的实用性。 本文提出基于约束采样RRT的机械臂运动规划方法,首先分析了标准RRT算法存在的问题,针对其在已探索空间内重复采样并拓展的问题提出稀疏节点产生机制,通过控制随机采样点产生的位置和数量减少在已探索区域寻找父节点的次数,从而减少随机树冗余节点数量和碰撞检测次数,加快探索未知区域;针对标准RRT算法拓展方向随机性过强的问题,提出动态采样域策略,通过约束采样区域的范围使采样域大小根据采样情况动态变化,确保采样兼具全局性和局部差异性的特点,进一步减少开阔区域的盲目搜索;同时,为避免局部拓展缓慢,引入贪婪策略,使步长动态变化,减少了开阔区域冗余节点的数量,提高了收敛速度;最后通过剔除规划路径中的冗余节点来缩短路径长度,用B样条曲线进行轨迹平滑,提高轨迹规划质量。通过在二维地图环境下的仿真实验和Robotic System Toolbox仿真实验以及ROS平台中机械臂的运动规划实验、真机避障实验,验证了所提算法的可行性和实用性。然而,DSSP-RRT算法仍保留了RRT算法的部分缺陷,例如规划路径的长度不是最优,随机树拓展因具有随机性而导致重复规划时轨迹不同,这些问题将是今后研究的重点。1.4 贪婪策略
1.5 路径处理
2 算法仿真实验和分析
2.1 仿真实验

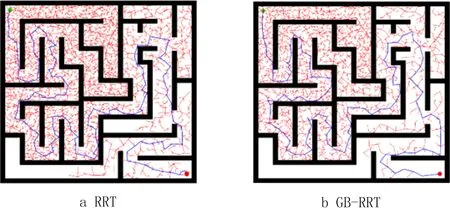
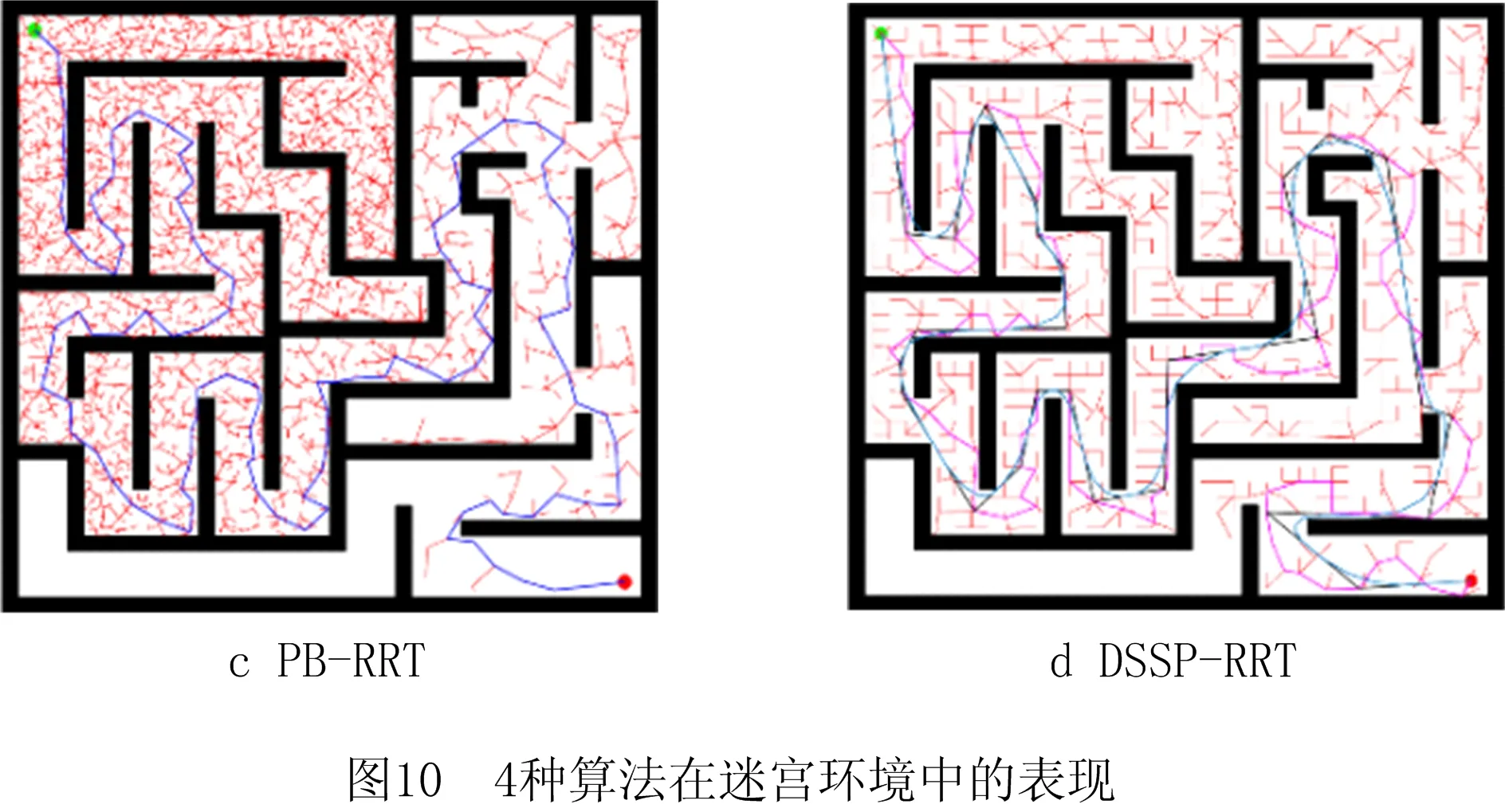
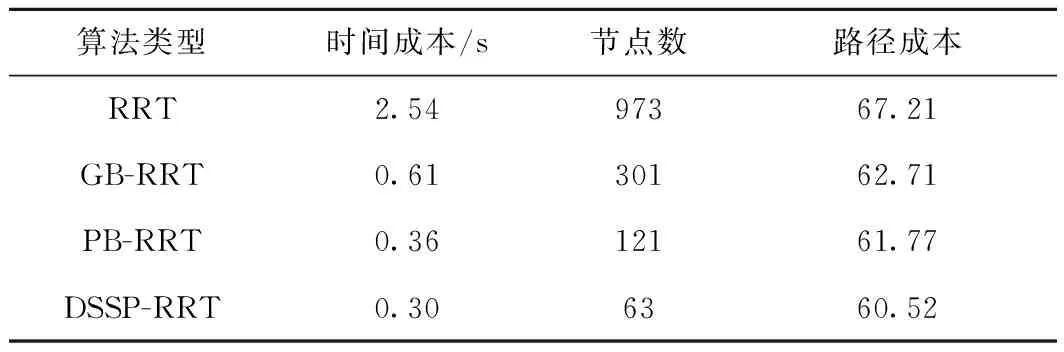
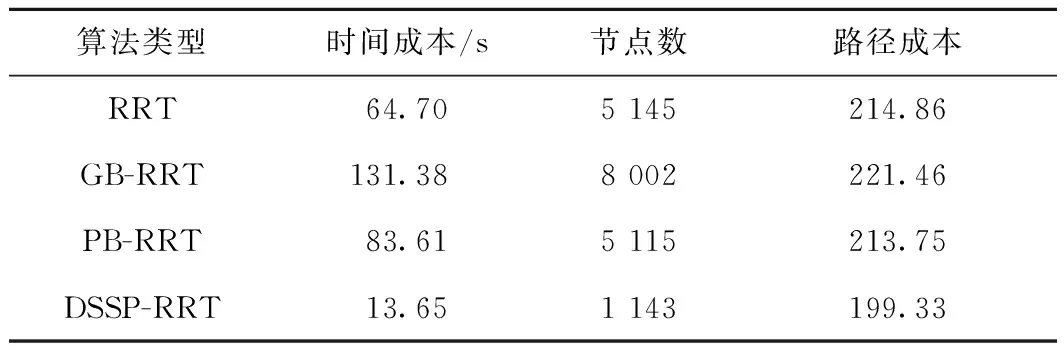
2.2 性能分析
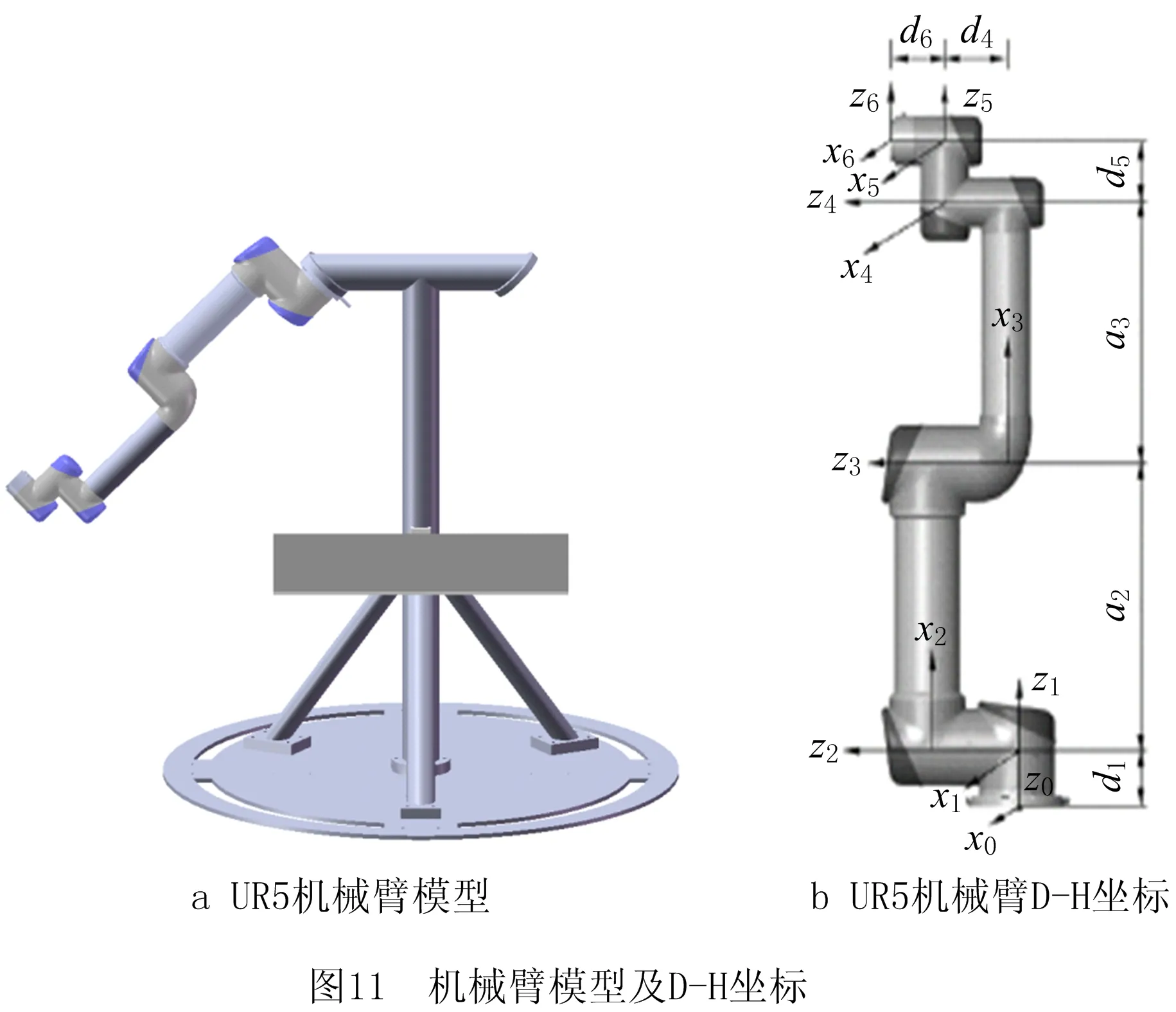
3 机械臂运动规划实验
3.1 机械臂运动学建模与碰撞检测
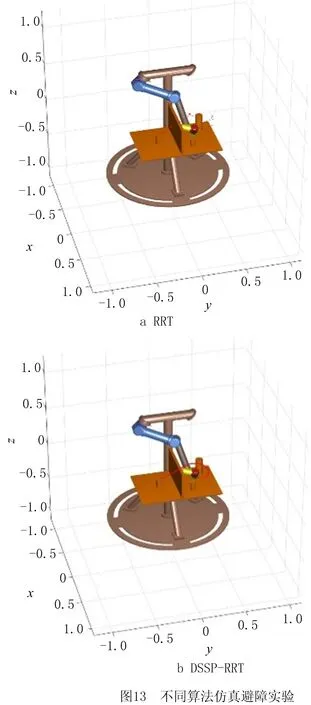
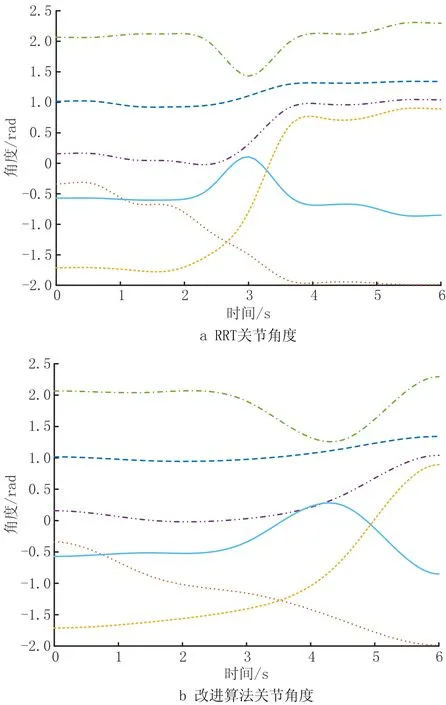
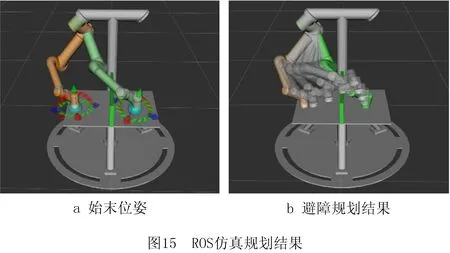
3.2 UR5静态避障实验


4 结束语
