基于改进遗传算法的移动机器人全局路径规划
2022-07-07俞旭阳刘成星
徐 兴,俞旭阳,赵 芸,刘成星,吴 祥
(1.浙江科技学院 机械与能源工程学院,浙江 杭州 310023; 2.浙江科技学院 信息与电子工程学院,浙江 杭州 310023)
0 引言
随着智能制造与电商经济的迅猛发展,适应性强、灵活性高和智能性好的仓储移动机器人需求呈井喷式增长,尤其在各类生产线及仓储物流中被大量运用,其中路径规划问题[1-3]一直是移动机器人领域的核心研究内容,其首要任务便是根据特定条件和环境规划出可供移动机器人高效稳定行走的无障碍路径,但移动机器人的路径规划属于NP(nonlinear programming)难题,只能根据问题寻求有效的近似算法而非精确算法。路径规划算法主要分为基于传统和基于群集智能策略两大类,传统全局路径规划算法包括人工势场算法[4]、Dijkstra算法[5]、A*算法[6]等,群集智能全局规划算法包括遗传算法[7]、蚁群算法[8-9]和粒子群优化算法等[10]。
已有大量学者开展了路径规划研究,刘二辉等[11]提出一种基于相连路径片段组成三角形使路径缩短的启发式变异规则,提高了路径的平滑度,改善了算法局部寻优能力;魏彤等[12]提出一种基于改进遗传算法的帧间关联平稳路径规划方法,提高了移动机器人的行驶效率和平稳性;马小陆等[13]提出一种基于势场跳点的蚁群算法,算法引入势场合力递减系数,减少了势场蚁群陷入局部最优的问题,提高了规划路径的平滑度;TUNCER等[14]针对移动机器人的路径规划问题提出一种新的遗传算法变异算子,用以避免算法早熟收敛,提高了遗传算法的收敛速度;刘子豪等[15]提出一种基于跳跃点搜索的改进A*算法,从而减小了计算量,提高了运算速度;AHMED等[16]提出一种多目标车辆路径规划方法,该方法利用精英非支配排序遗传算法对路径长度、路径安全性和路径平滑度进行优化,在解决复杂路径规划问题时具有鲁棒性和高效性;徐力等[17]针对现有遗传算法易陷入早熟、收敛速度慢等问题,提出一种基于自适应遗传算法的机器人路径规划方法,虽然能较好地避免陷入局部最优,但是仍需要较大的初始种群,降低了算法的计算效率。
上述诸多路径规划研究中,文献[12]未能很好解决算法应用时易早熟、效率低的问题;文献[14]虽然改进了算法效率,但是应用时仍然存在较大的局限性,且路径平滑度不高;文献[17]虽然针对算法的早熟问题提出相应的措施,但是仍然存在收敛迭代过慢、效率低的问题。综合考虑常规路径规划算法规划路径非最短、平滑度较差、效率低和极易早熟等问题,本文提出一种基于灾变策略的改进遗传算法(Improved Catastrophe Genetic Algorithm, ICGA),算法有如下改进:①改进初始种群生成方法,大幅提高了算法前期的计算效率;②改进灾变算子极好地避免了算法早熟;③加入筛选步骤的交叉算子提高操作效率;④重新设计动态变异算子提高后期的局部搜索能力;⑤在适应度函数中加入路径转角、转弯次数权值等多约束条件,提高路径的平滑度。仿真结果证明,相比遗传算法(Genetic Algorithm, GA)、改进的自适应遗传算法(Improved Adaptive Genetic Algorithm, IAGA)和启发式通信异构双种群蚁群优化算法(Heuristic communication Heterogeneous dual population Ant Colony Optimization algorithm, HHACO),在多次规划时ICGA能更好地避免出现早熟,减少算法的寻路时间,保证较高的路径质量。最后将算法移植到机器人操作系统(Robot Operating System, ROS)平台中,经WHEELTEC小车导航试验证明,ICGA比IAGA规划的路径更优,效率和稳定性更高。
1 工作场景建模和路径规划模型
1.1 移动机器人工作场景建模
为给移动机器人导航提供可靠的环境信息,采用栅格地图对现实场景进行建模,如图1所示。对场景进行单元化分割,地图中黑色栅格表示障碍物。采用矩阵G存储地图信息,其中1和0元素对应栅格地图中的障碍栅格和可行栅格。
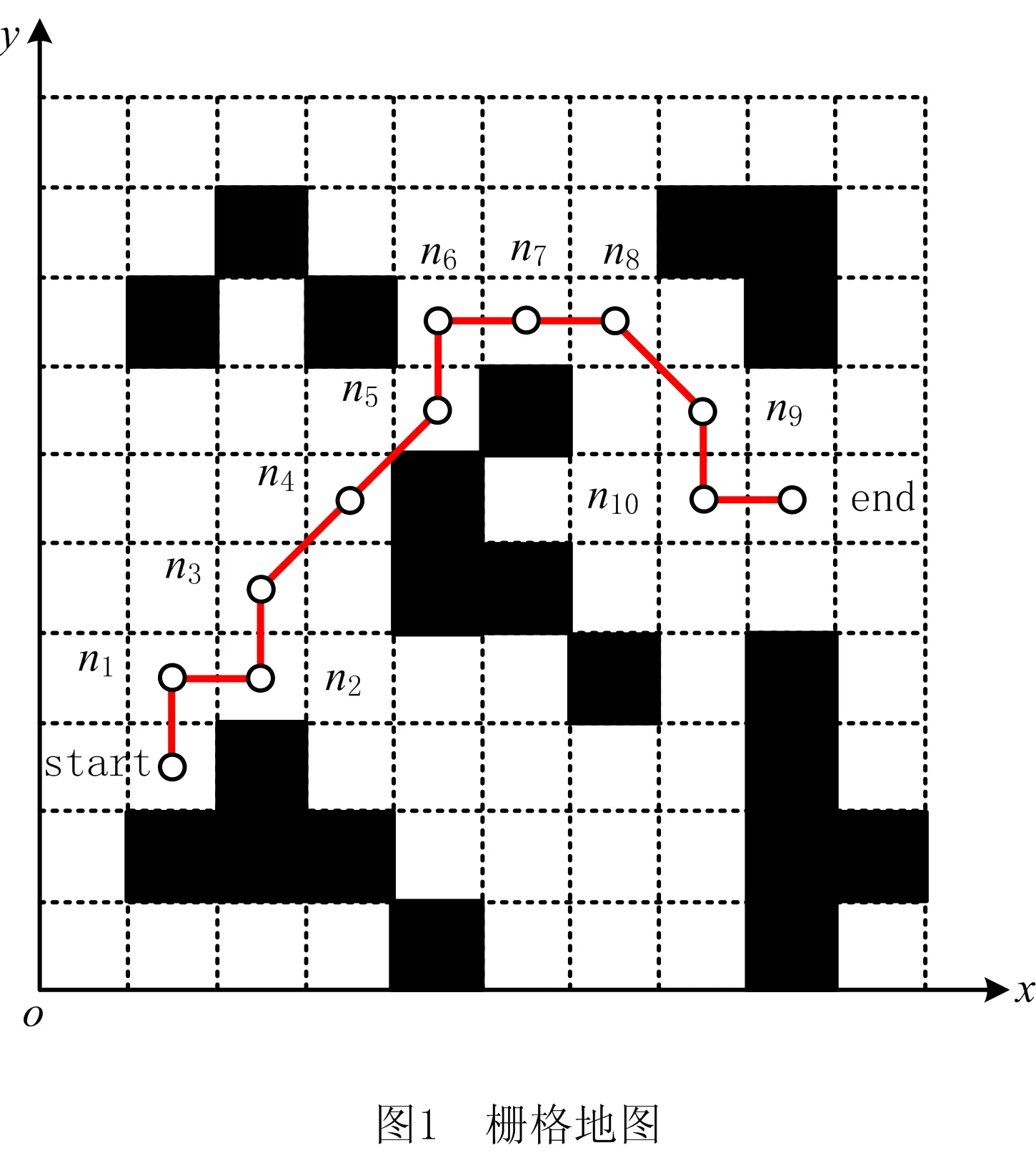
栅格地图和矩阵G的对应关系为
Map(x,y)=G(x,y)。
(1)
1.2 路径规划模型
采用实数编码的方式,由下往上、从左到右的顺序逐列编号,索引函数(xndx,yndx)=in2sub(siz,ndx)中栅格编号和坐标的关系如下:
k=cumprod(siz);
(2)
yndx=rem[(ndx-1)/k]+1;
(3)
xndx=(ndx-yndx)/k+1。
(4)
式中:ndx为编码号;siz为地图矩阵的行列数向量;(xndx,yndx)为编号ndx在地图中的坐标;rem()为整除取余函数;cumprod()为求连乘积函数。
逐列对栅格地图编号后,路径可用染色体基因表示,如图1中路径所示,无障碍路径可以表示为Pi=[startndx1ndx2ndx3…ndx8ndx9… end]。
2 基于改进遗传算法的路径规划方法
2.1 问题描述及适应度函数设计
考虑移动机器人的作业效率与稳定性,要求机器人在作业时移动距离最短、转向角度最小且非必要转向次数最少,因此需对算法提出路径长度、路径转角和转向次数的多目标优化要求,则上述问题可描述如下:
s.t.
p∈C;
C∈G。
(5)
式中:F为向量目标函数;p为满足条件的路径;C为路径集合;G为地图矩阵。
根据式(5)中的问题描述设计多约束适应度函数
(6)
(7)
(8)
(9)
式中:fit1为路径长度;fit2为路径角度;Tnum为路径中的转向次数;ω1,ω2,ω3为权值系数;PRECI为节点数,(xi,yi)为节点坐标;Γ()为条件函数,θ为路径中的转向角度,若θ≠0°,则Γ(θ)=1。
2.2 改进种群初始化方法
初始种群的特性对算法效率有重要影响,传统GA常用一种随机搜索可行路径的方法[18],该方法产生可行路径的速度较快,但初始路径质量较差,筛选法则效率低下,因此本文提出一种基于分段A*算法的区域必经点选择策略生成初始种群的方法,步骤如图2所示。
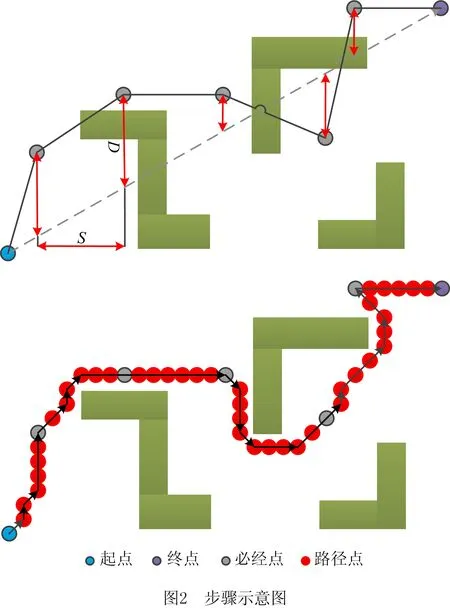
具体步骤如下,:
步骤1设置起点、终点与基准线。根据Dmax确定选择路径必经点的区域。
步骤2根据纵向随机范围D和横向随机范围S确定区域,并选择分布在基准线两侧的必经点。
步骤3使用A*最短路径算法联接路径必经点:
Si=randi(|xSp-xEp|/Nm);
(10)
Di=±randi(Dmax)。
(11)
式中:Si为必经点的横坐标;randi()为随机函数;xSp,xEp分别为路径起点和终点的横坐标;Nm为必经点的个数;Di为必经点的纵坐标;Dmax为最大区域阈值;下标i为必经点的索引值,i=1,2,3,…,N。
种群个体多样性减少是导致早熟的原因之一,为此引入路径海明距离作为种群个体相似度评价的标准,其中路径对应点用式(12)选取,从两条路径中找到距离最近的一对点,若两点间的距离满足ε=0,则判定为对应点对,路径相似度则为对应节点数在总路径节点中的占比;然后设计一种以种群个体间平均相似度为标准的种群评价函数,如式(13)~式(15)所示。
(12)
式中:Cor()为满足距离条件的相似点对计数函数;Г()为属于不同路径中两节点间的距离判别函数,若节点P1(i)与P2(j)间的欧式距离为ε,则Г(P1(i),P2(j))=1,反之为0。
(13)
(14)
(15)
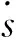
表1所示为3种方法在4类地图中所生成路径参数的对比,包括平均适应度、相似度和消耗时间。比较消耗时间可见,小规模地图中随机法具有优势,随着地图规模的增加,区域法的优势逐渐凸显;比较相似度可见,随机法与加入筛选步骤的随机法各具优势;比较适应度参数可见区域法最优。综上可知,区域法能大幅提高适应度值,降低消耗时间,提高算法前期的收敛速度。
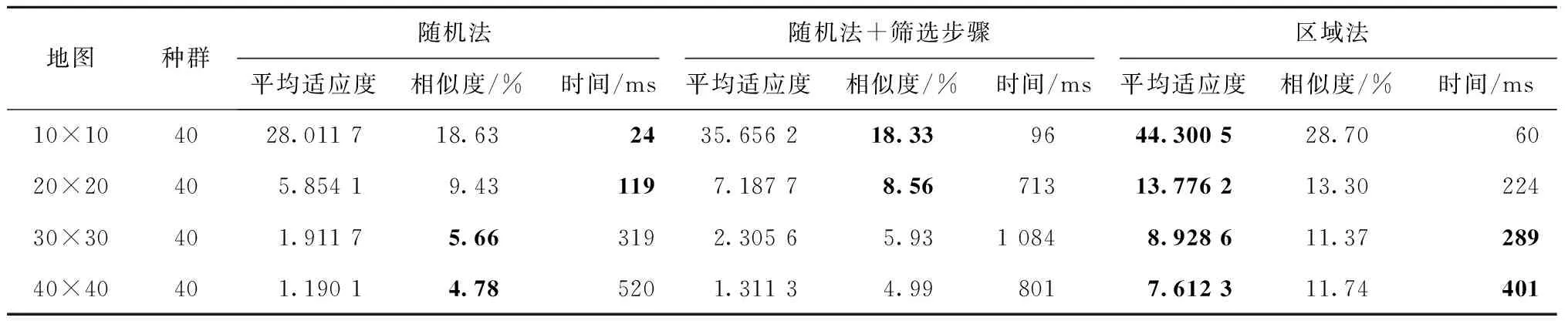
表1 生成方法对比
2.3 改进遗传算子
(1)改进选择算子 常规GA中常采用轮盘赌选择方法,但因为种群规模限制和随机操作等,单独使用轮盘赌方法误差较大,易丢失优秀个体,所以采用随机遍历抽样法配合基于优胜劣汰的精英替代算子。其中个体选择概率
(16)
式中:NIND为个体数;eval()为个体Uk的适应度值计算函数。
因为随机遍历采样法中需要等距离地选择个体,所以将npoint设为需要选择的个体数,等距离地选择个体每个选择指针的距离1/npoint,选择的起始位置由[0,1/npoint]之间的均匀随机数决定,如图3所示。
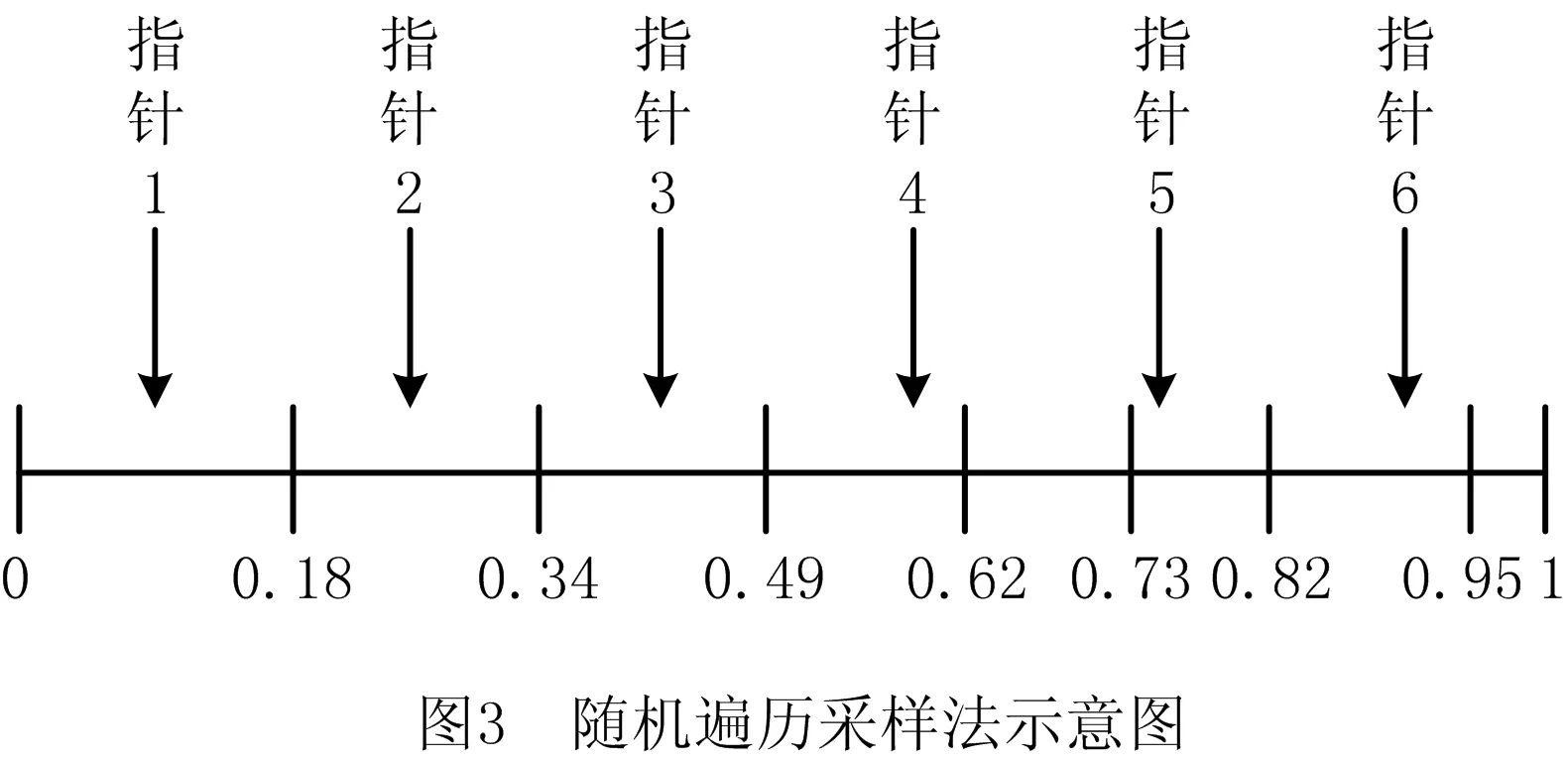
随机遍历抽样算子选取个体后,精英替代算子根据子代的适应度值替换父代种群中较差的个体,完成优胜劣汰操作,保证父代种群中优秀的个体不会因选择误差而被淘汰。
(2)改进交叉算子 采用单点交叉的方式,交叉点选择两条路径的对应点。由于选择算子的特性,随着算法迭代种群逐步被高适应度个体占据,种群中将存在大量相同的个体,而相同个体间的交叉是无效的;为防止相似度为100%的两个个体交叉,设计了一种快速判别是否交叉的方法,而且为了消除计算相似度带来的高时间复杂度,本文采用路径长度和栅格号的累加值作为判断依据进行快速筛选,如式(17)所示。若E()=1则放弃当前次的交叉操作,避免无效交叉,节约计算资源和时间。为加大交叉算子的搜索能力与路径可行性,若不存在相同的栅格节点,则随机选取两条路径的不同位置进行交叉;若交叉后路径可行,则用插入算子填补交叉点处的空白栅格,若路径不可行,则放弃此次交叉。
i≠j。
(17)
式中:E()为相似度评价函数;α1=1.5,α2=0.1均为权值系数;Pi,Pj分别为某两个路径个体;Pi(q),Pj(r)分别为路径个体中的某两个栅格号;PRECIi,PRECIj分别为两个路径个体的栅格数。
(3)改进变异算子 常规变异方式是在染色体随机位置上替换基因完成变异操作,例如文献[12]的变异算子采用替换该位置八邻域基因的方法和删除该染色体任意位置基因的方法。虽然上述方法有较大的变异成功率和路径可行性,但是仍然存在局部搜索能力不足的问题,因此本文提出一种内嵌A*算法的动态变异方法,步骤如下:
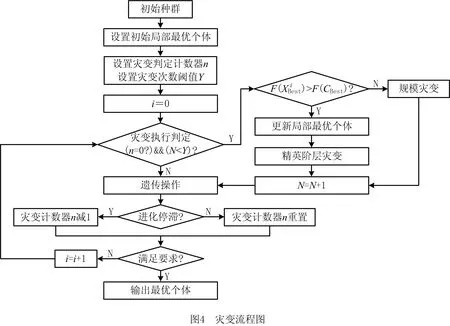
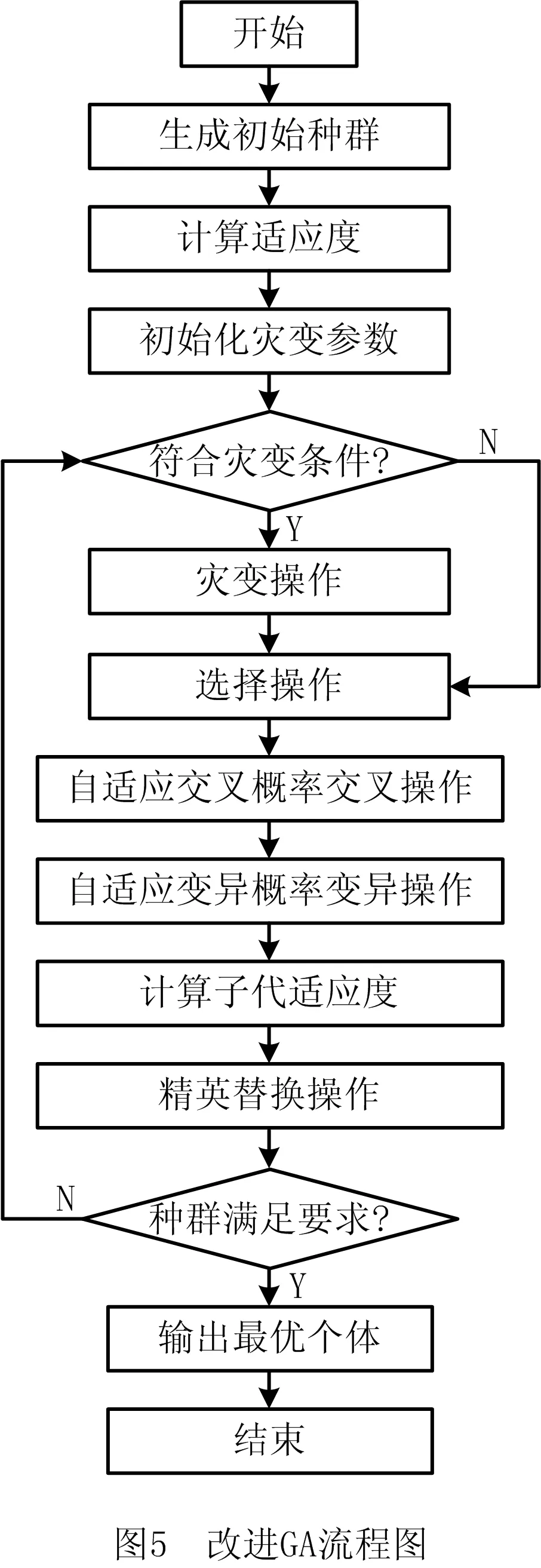
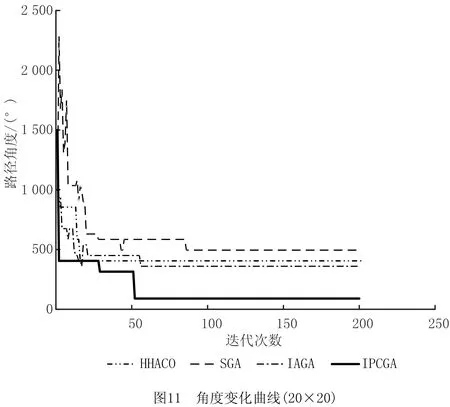
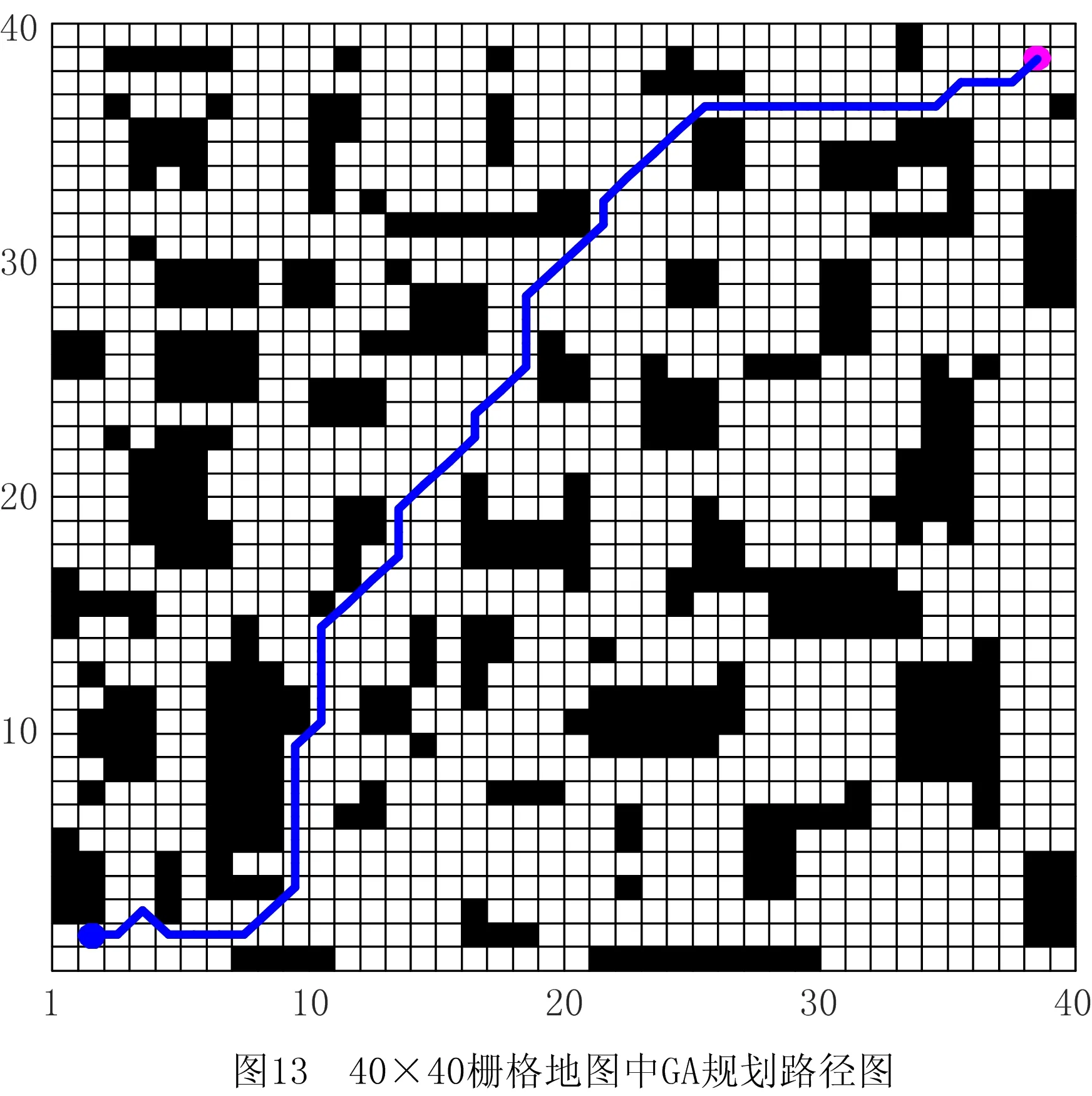
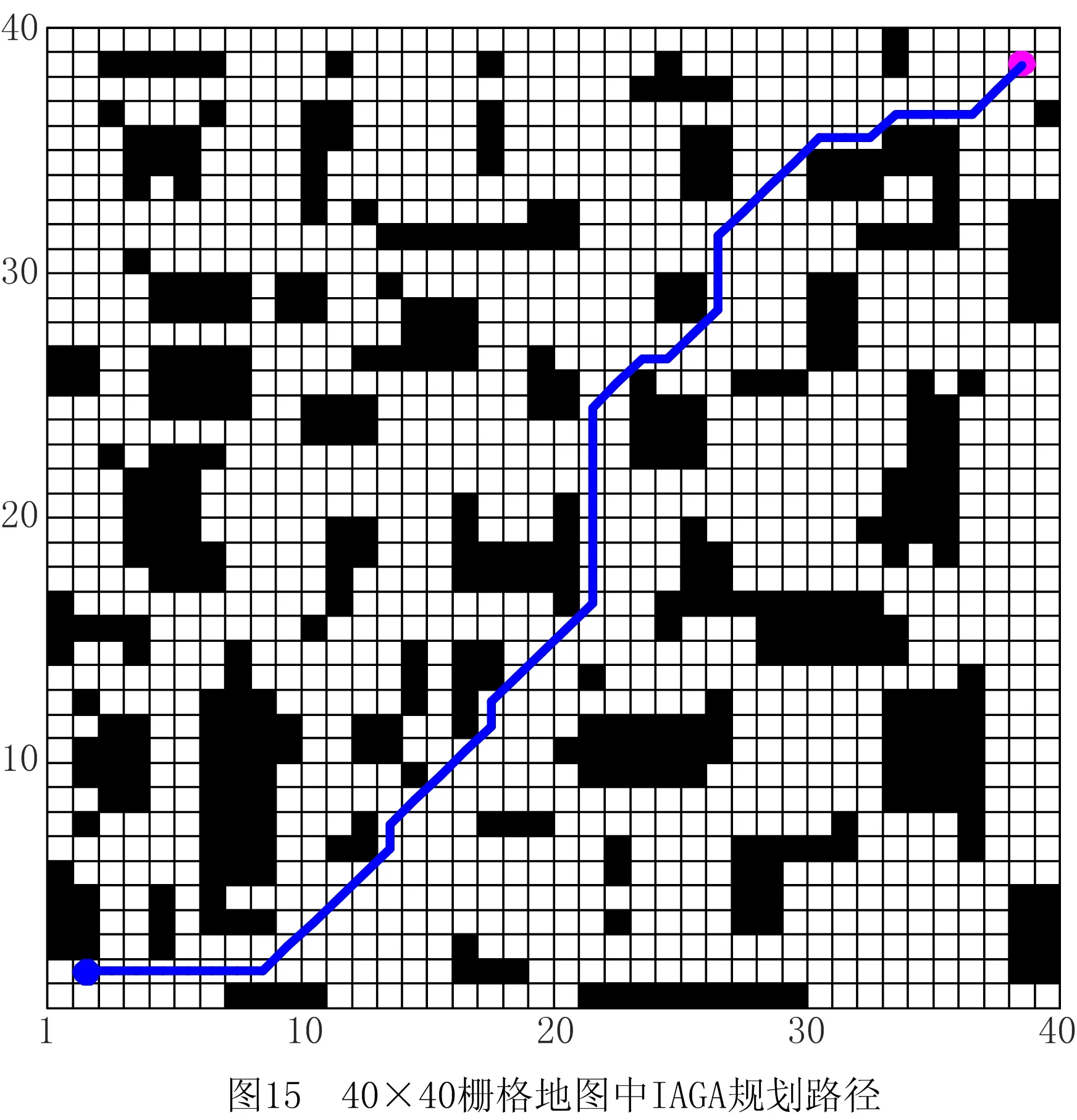
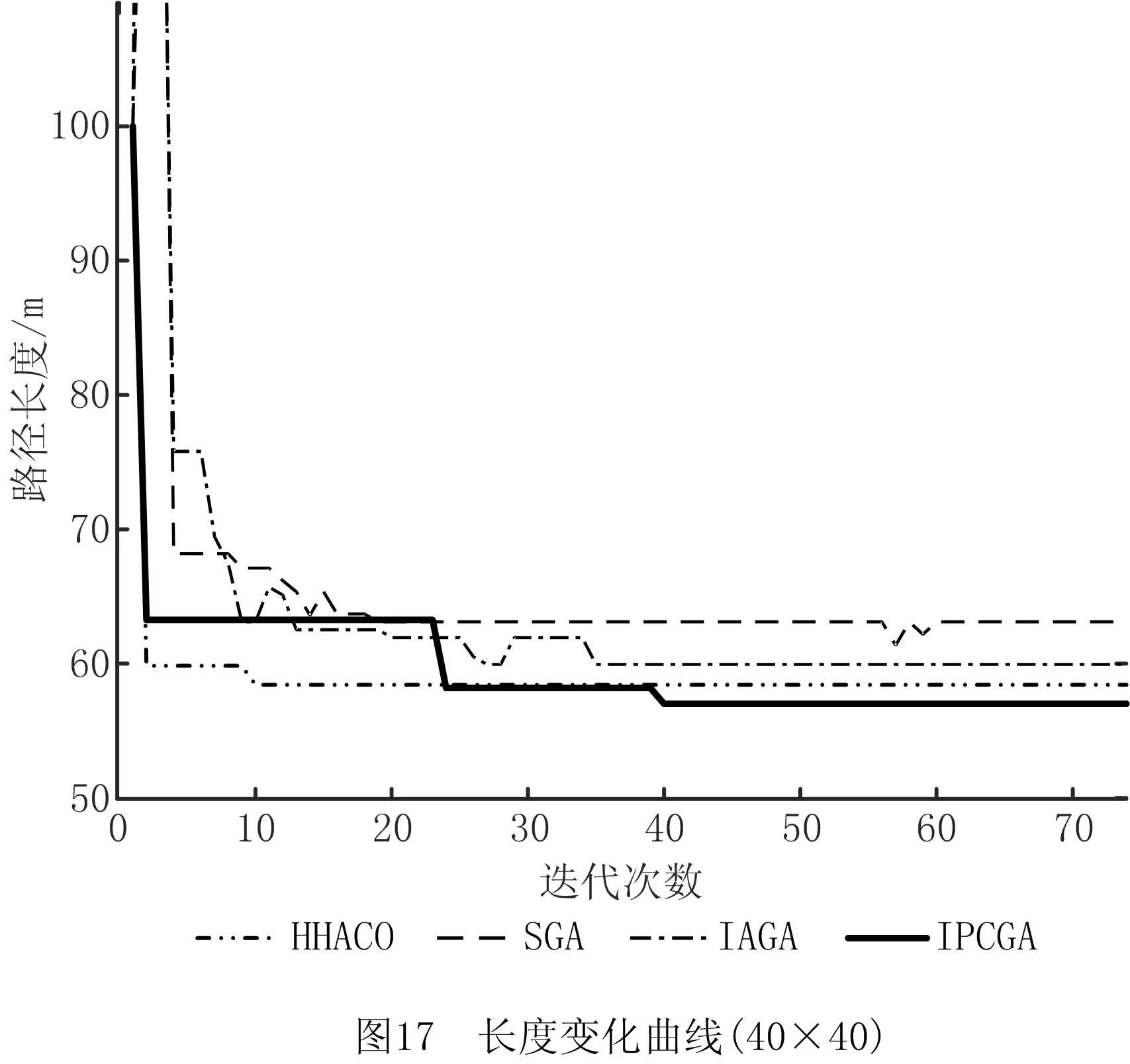
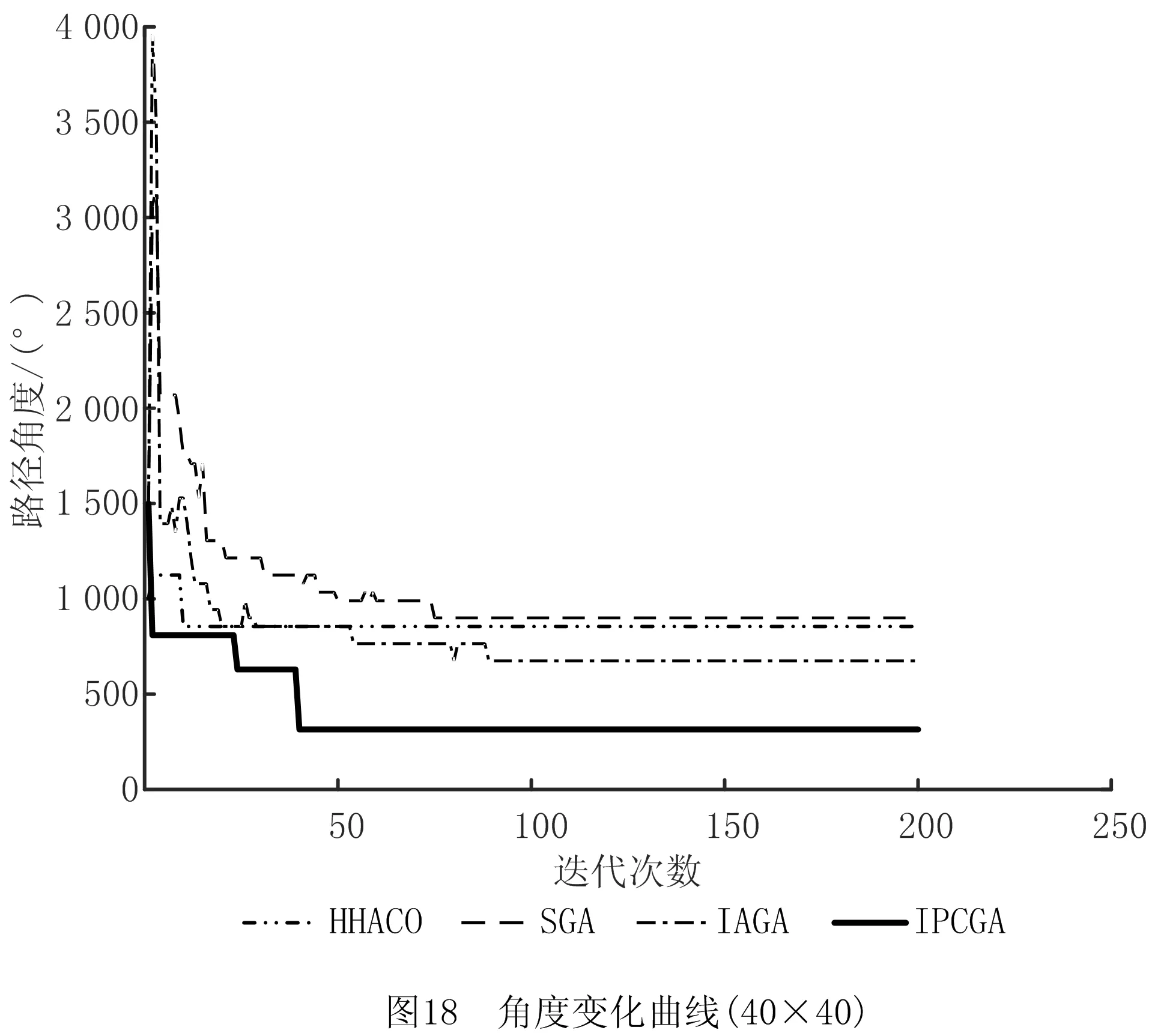
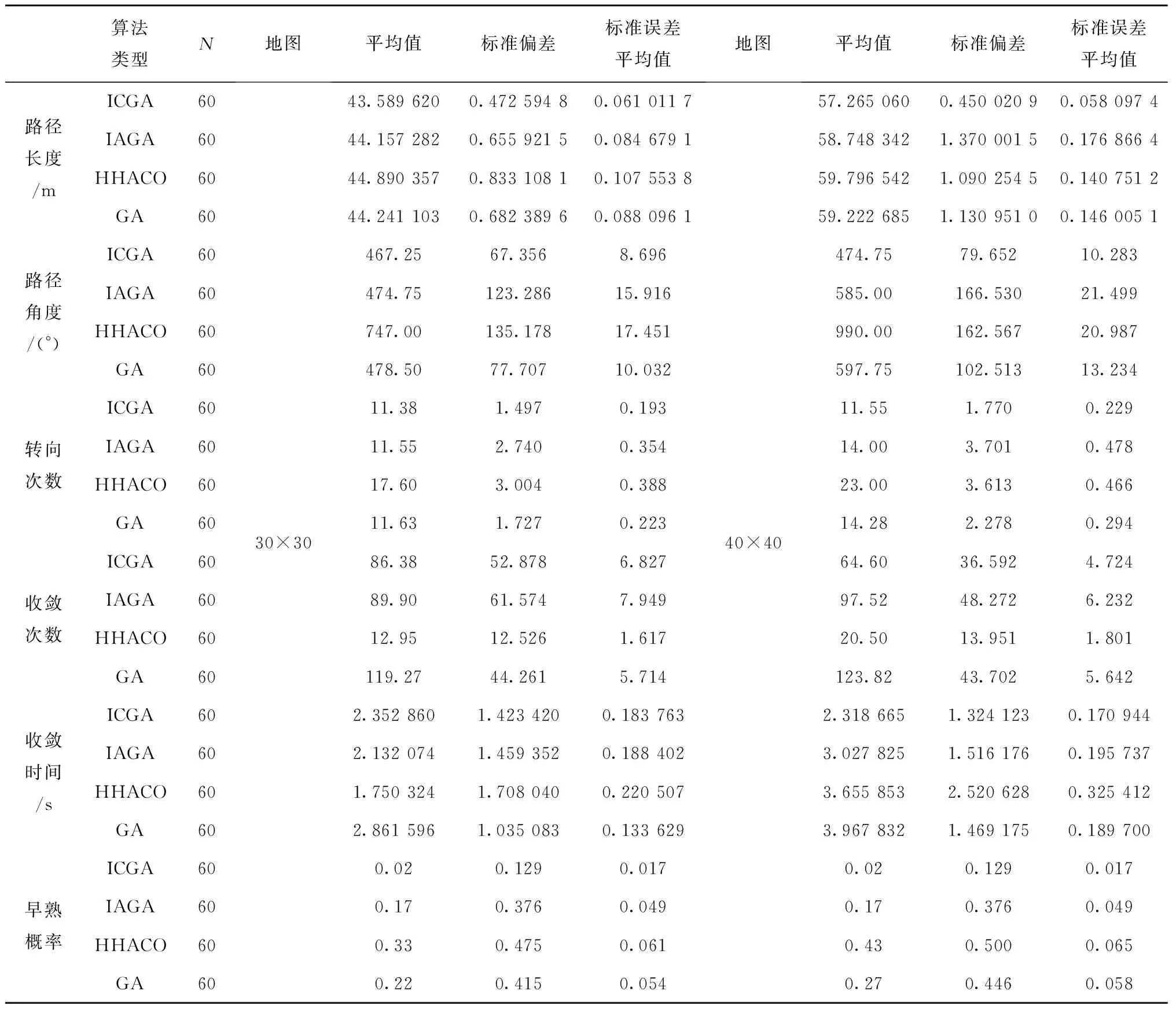
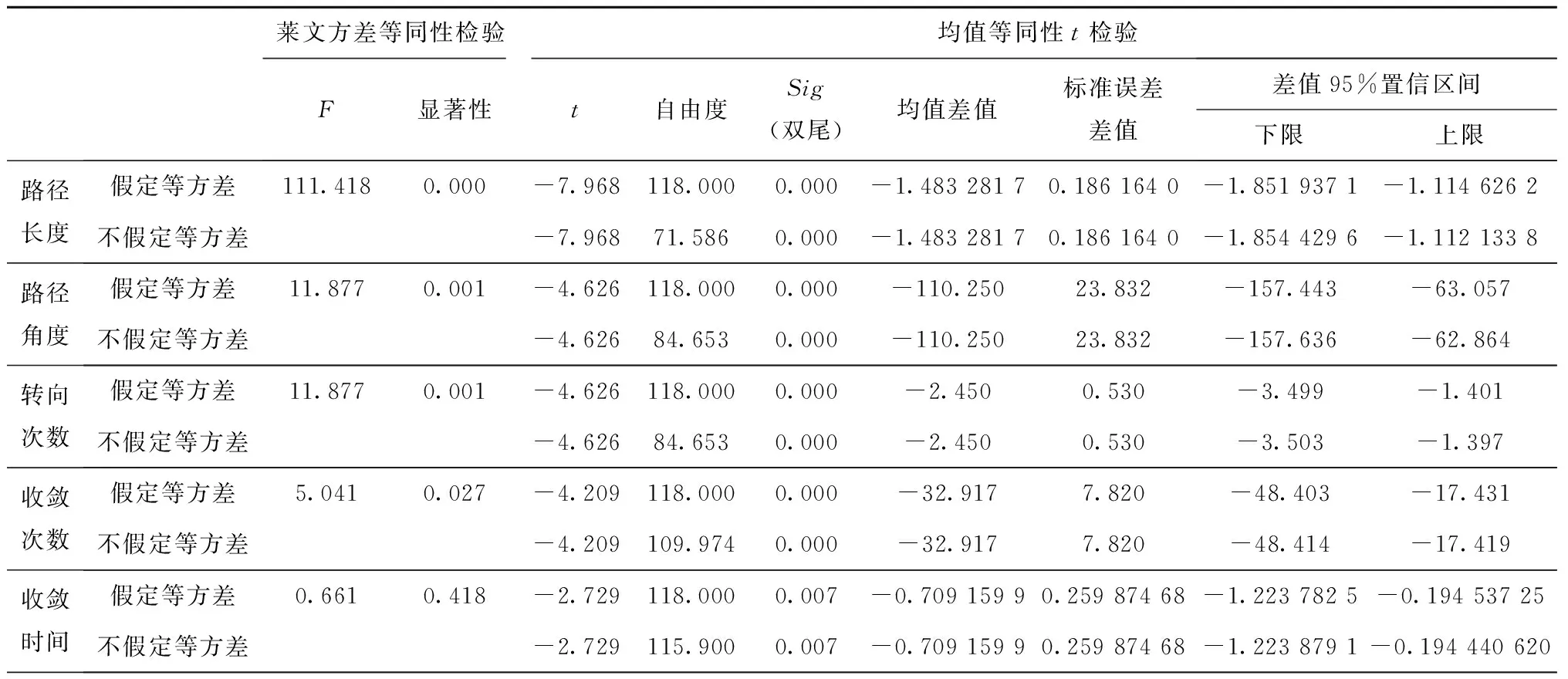
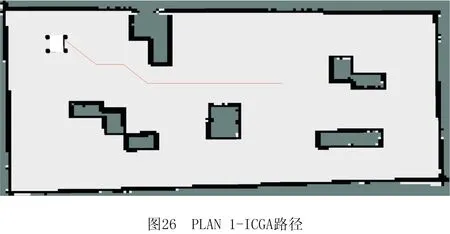
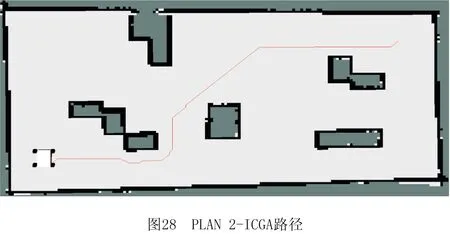
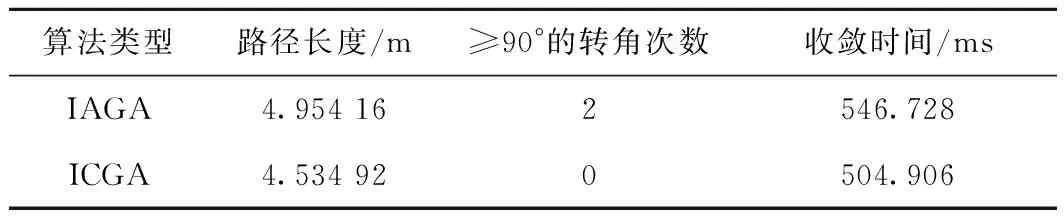
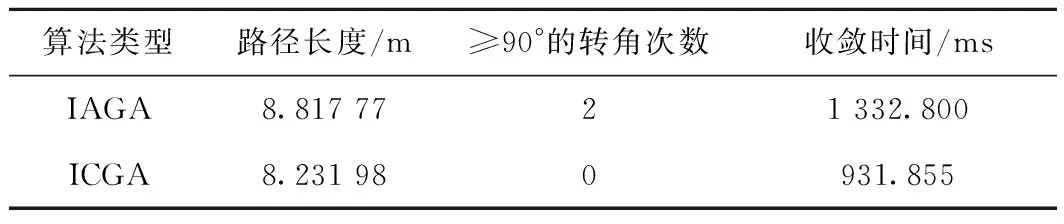
步骤1用Pm控制当前个体是否变异,若随机数r 步骤2动态选择染色体中变异路段的长度,随机选择路径中的两个栅格,栅格间的距离由种群进化程度决定。进化初期选取的变异路径段长度应尽量短,后期为帮助算法跳出局部最优,则应加大该路径段的长度。 步骤3采用A*算法再规划路径替换两个栅格间的局部路径。 (4)插入算子 为保证路径中每个栅格节点间的连续性,引入一种路径间断连续方法[18],步骤如下: 步骤1按式(18)判断路径中每两个相邻栅格节点间是否连续。 L=max{abs(xi+1-xi),abs(yi+1-yi)}。 (18) 式中:x,y为栅格节点的横纵坐标;上标i,i+1为路径中该节点的次序;abs()为绝对值函数;max()为最大值函数。 步骤2若L≠1则两栅格间断,按式(19)获得这两个栅格的中点栅格,若中点栅格为障碍栅格,则取该栅格周围八邻域中的任意栅格。 (19) 式中:上标mid表示待插入的中间栅格;int()为取整函数。 步骤3将中点栅格插入两间断栅格中间,为防止算法陷入死循环,判断中点栅格是否已在路径中,是则重新选择,返回步骤1检查路径是否存在间断,若路径处处连续则跳出循环。 交叉变异概率是影响算法行为和性能的关键,合理的交叉、变异概率能显著提升算法性能,因此本文引入一种自适应调整交叉变异概率的方法[19],在进行交叉变异操作前自适应调整概率。交叉概率Pc和变异概率Pm分别为: (20) (21) 式中:k1,k2分别为交叉、变异概率缩放系数,k1,k2∈[0.5,1];Pc1=1,Pc2∈[0.5,1];Pm1=0.1,Pm2∈[0.05,0.1];Fm为待变异个体的适应度值,Favg为种群中个体的平均适应度值,Fmax为种群中个体的最大适应度值,Fc为两个待交叉个体中较大的适应度值。 GA在实际应用中极易发生未成熟收敛(又称早熟),由于进化后期种群中的个体趋于一致,经遗传操作已无法产生更优个体,种群陷入进化停滞状态。为此,本文改进了一种灾变策略,帮助算法跳出停滞而搜索到最优解。 根据灾变论的观点,每当发生毁灭性的自然灾害时,大部分生物被灭绝,灾变结束后造物主结合原有物种创造出稍有不同且更富竞争力的新物种,该过程大大提高了进化进程,而将这一策略加入GA能极大帮助算法避免早熟,保持其应有的性能。灾变策略实施流程如下:种群经过n代进化后无法产生更优个体时,执行灾变操作,将灾变判定计数值作为灾变操作执行的条件,若在一次遗传操作后当前种群没有产生更优个体,则计数器减1,否则计数器重置初值;若计数器值归零,则表示局部搜索已充分满足灾变条件;设置灾变上限次数,若在执行N次灾变操作后,局部最优个体仍未发生变化,则认为全局搜索已充分,当前局部最优个体即为全局最优个体,算法结束。 灾变策略的步骤具体如下: (2)种群在数次遗传操作后,灾变计数器归零,满足灾变判定条件,执行灾变预操作,有两种情况: 流程如图4所示。 综上所述,改进GA的流程图如图5所示。 (1)按方法1产生初期种群。 (2)设定灾变计数器(即种群进化停滞计数)和灾变次数阈值Y。 (3)判定灾变,若种群产生新个体则灾变计数器重置,否则减1;若计数器为零且灾变次数未达上限,则执行灾变,否则转(4)。 (4)执行遗传操作。 (5)将子代种群个体逐一与父代种群个体比较,替换父代种群中竞争力较差的个体。 (6)循环执行(3)~(5),直至找到全局最优个体。 (7)输出最优路径,算法结束。 为验证ICGA的有效性,采用MATLAB 2016a平台进行编程仿真,分别对GA[18],IAGA[20],HHACO[21],ICGA进行仿真,在不同规模的栅格地图(其中20×20,30×30分别引用自文献[17]和文献[13],10×10,40×40为随机障碍地图)中分别进行60次路径规划比较,算法参数如表2所示。 表2 算法参数设置 设置栅格边长为1 m,起点、终点分别为左下点和右上点。图6~图9所示为4种算法在20×20栅格地图中的路径规划结果,图10~图12所示为4种算法的路径长度、角度和适应度变化曲线,图13~图16所示为4种算法在40×40栅格地图中的路径规划结果,图17~图19所示为4种算法的路径长度、角度和适应度变化曲线。 由图10~图12和图17~图19所示的算法性能变化曲线可见,GA,HHACO,IAGA规划的路径存在冗余,其中GA路径长度过长,HHACO,IAGA包含过多的非必要转向次数,而ICGA则能在路径最短的前提下减少非必要转向次数,提高路径平滑度。 表3和表4所示为不同地图中60次路径规划的比较和统计结果,综合分析可知,在不同规模地图的多次路径规划试验中,HHACO收敛速度最快,但早熟概率最高,极易导致路径质量严重下降;GA收敛速度最慢,且路径平滑度较差;IAGA的收敛速度和平滑度有所改善,但仍然容易早熟;ICGA则能在搜索到最短路径的同时大幅减少非必要转向次数,不但能提高路径平滑度,缩短寻路时间,而且在多次规划时能有效降低算法出现早熟的概率。 表3 不同规模地图中的仿真组统计1 表4 不同规模地图中的仿真组统计2 为了证明算法的有效性,排除偶然因素和抽样误差,本文引入小概率原理并进行显著性检验,若Sig≤0.01,则表明两者存在极其显著的差异。表5所示为两种算法(ICGA和IAGA)在40×40地图中的60次独立样本检验,其中评价性能各项值的Sig均小于0.01,说明两种算法的规划路径样本存在明显差异,因此本文所提ICGA是有效的。 表5 40×40地图中的算法(ICGA和IAGA)独立样本检验 续表5 图21所示为小车的硬件结构,图22所示为雷达测距原理图。激光雷达扫描后获得障碍物的点云数据,将其与STM32控制板的编码器信息反馈给ROS主控制器,主控制器计算速度信息并返回至STM32控制板,由STM32控制板控制WHEELTEC四轮小车实现自主导航。 为验证本文算法,将ICGA与对比算法移植到基于Ubuntu 18.04的ROSmelodic机器人操作平台中,试验所采用的机器人为WHEELTEC四轮小车,该机器人搭载Jetson TX2主控和STM32底盘控制板,如图20所示。 图23所示为ROS平台整体框架原理图,其中move_base包为ROS导航提供各类接口,主要包括全局路径规划(global planner)和本地实时规划(local planner)。本次试验只需根据给定的目标位置规划总体路径,因此只用nav_core包中nav_core::BaseGlobalPlanner的预留接口为规划器编写一个新类,新规划器包括路径规划所需的核心库,并将ICGA路径规划算法添加为一个新的全局路径规划器,使move_base能够调用本文算法的全局路径规划器。 选取实验室作为试验场景,如图24所示。利用gmapping建图和amcl自定位模块完成试验环境的二维建图,用Rviz作为查看导航路径的可视化工具,并设置两次导航任务PLAN 1和PLAN 2,结果如图25~图28所示。可见,在短距离导航任务1和长距离导航任务2中,IAGA规划路径都出现了≥90°的转角和大量的非必要转向,其中大转角在移动机器人导航中最致命,其增加了机器人的碰撞概率,降低了机器人作业的稳定性和效率。通过分析表6和表7所示的规划结果可知ICGA规划的路径更优。该路径不但更短,而且大幅减少了大转角和非必要转向次数,大大增加了移动机器人的行走稳定性、效率以及驱动电机的使用寿命。 表6 PLAN 1两种算法路径规划结果对比 表7 PLAN 2两种算法路径规划结果对比 本文针对GA在路径规划应用时极易出现早熟、效率低、路径平滑度差等问题:①在IAGA的基础上,加入并改进了条件灾变策略,帮助算法跳出局部最优,同时增加个体多样性并减小种群规模来提高算法效率;②利用重新设计的区域必经点选择策略提高初始种群的质量,来提升算法初期的收敛速度;③采用带有筛选步骤的改进交叉算子避免相同个体间的无效交叉,节省计算资源;④通过改进内嵌A*算法的动态变异算子加大算法后期的局部搜索能力,并采用改进的多约束条件适应度函数大幅提高路径平滑度。通过不同规模地图的仿真试验证明,ICGA的路径搜索速度、早熟概率和路径质量均优于常规算法,经ROS平台导航试验证明,ICGA规划器规划的路径较常规路径规划器更优、效率更高。2.4 自适应策略
2.5 灾变策略
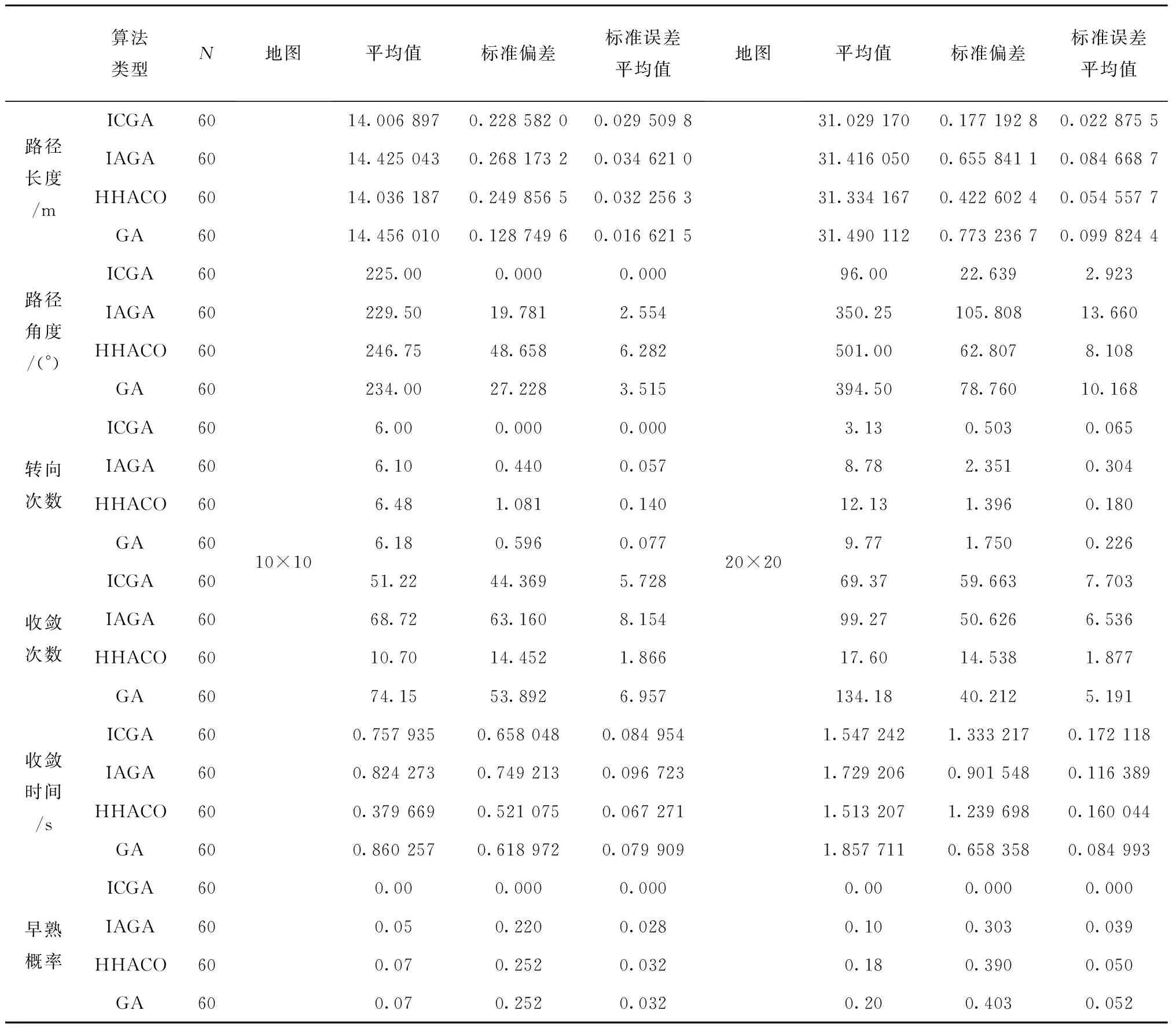
3 试验及结果分析
3.1 MATLAB仿真试验

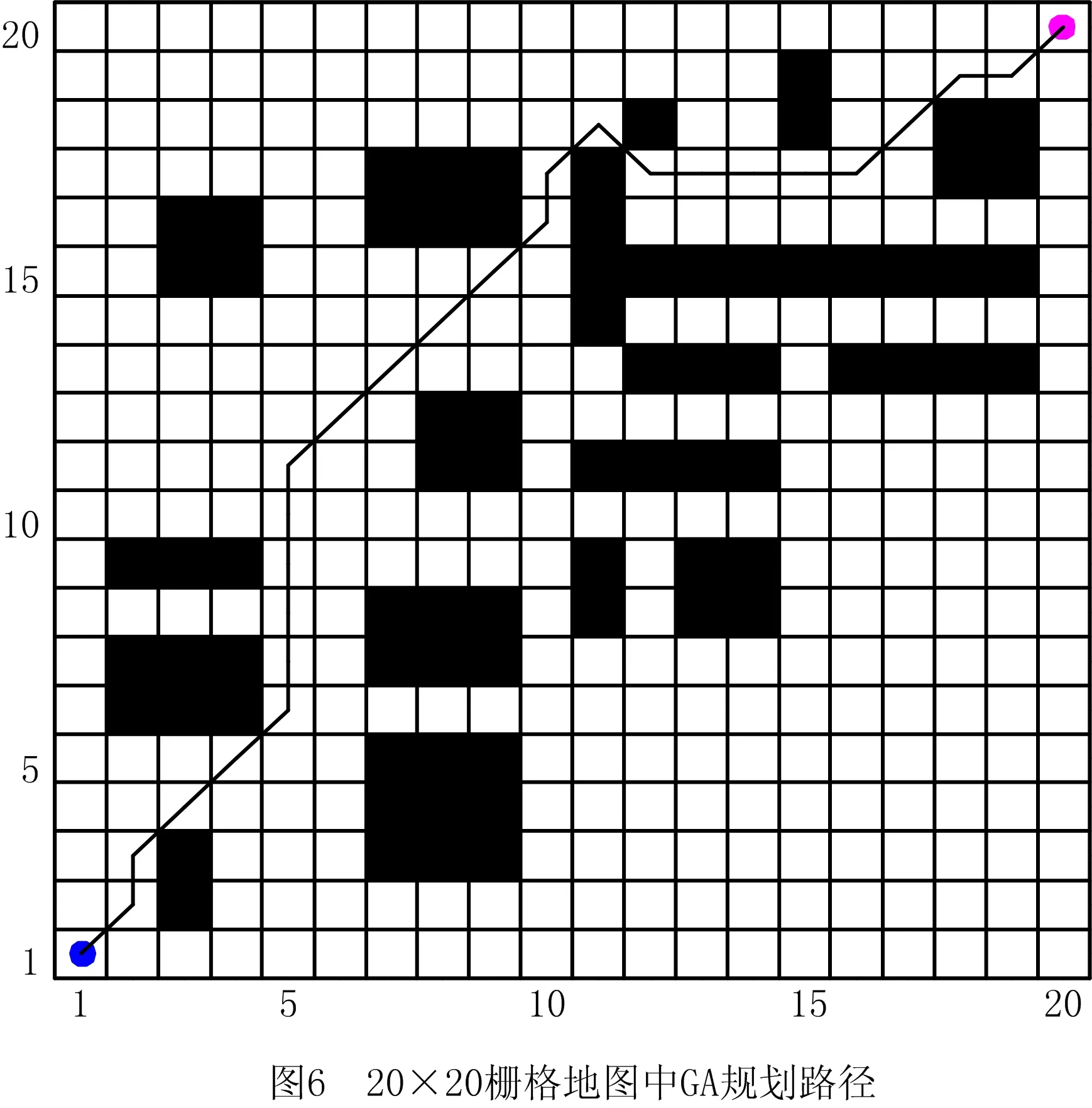
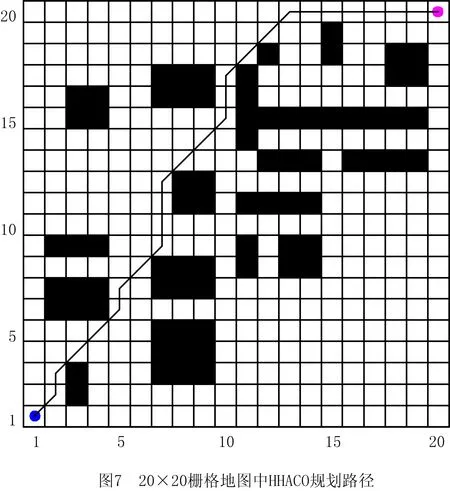
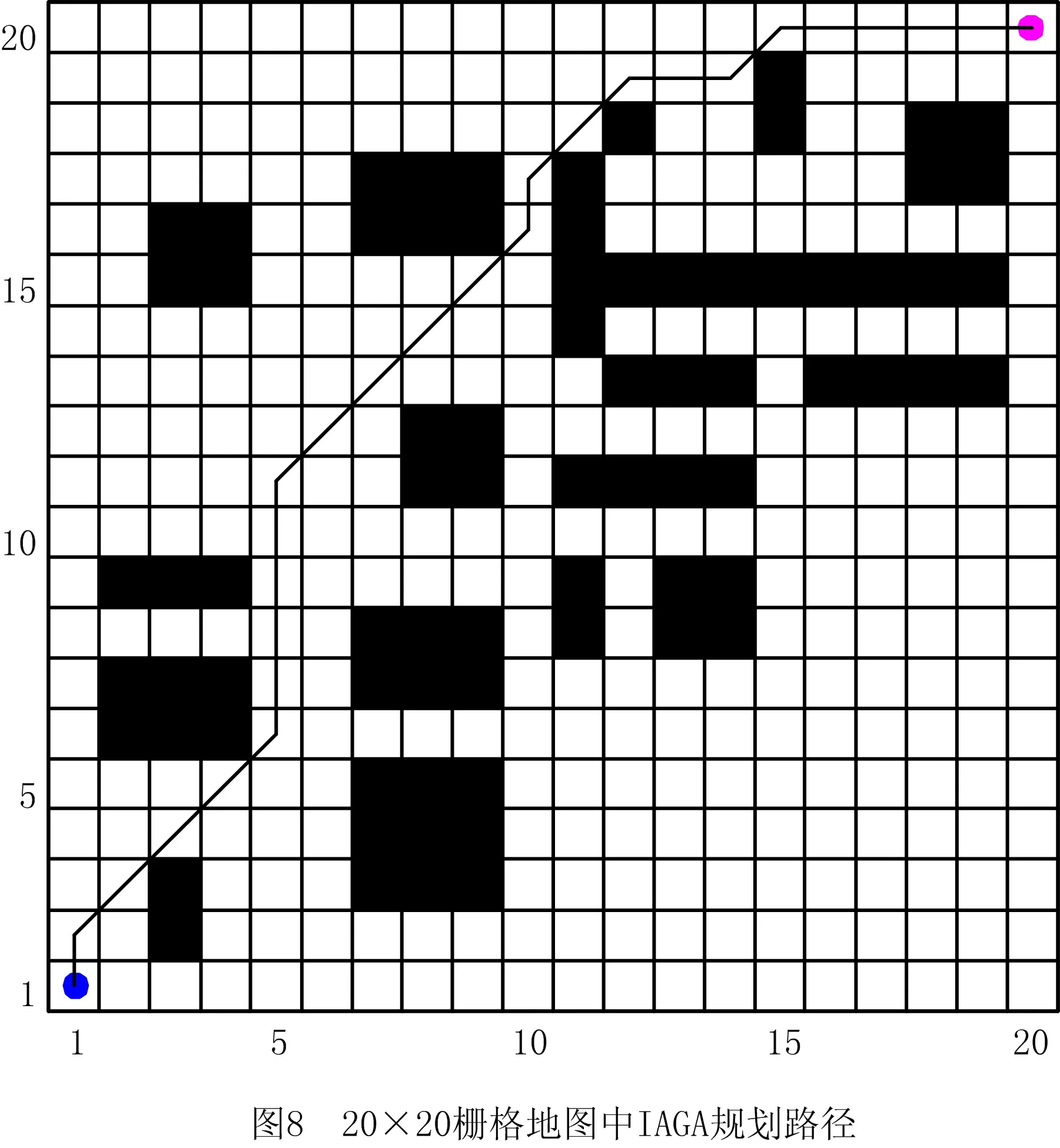
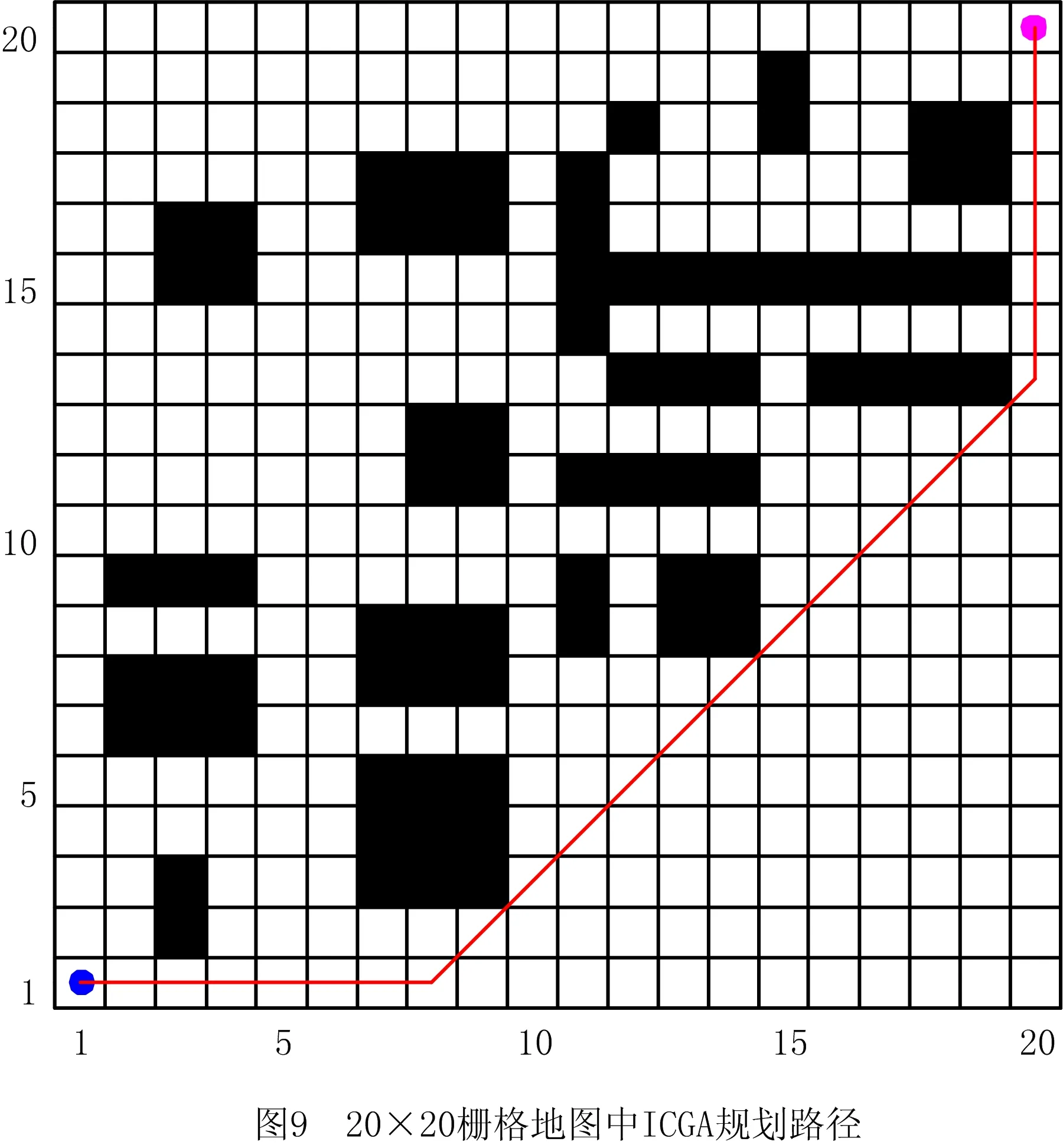







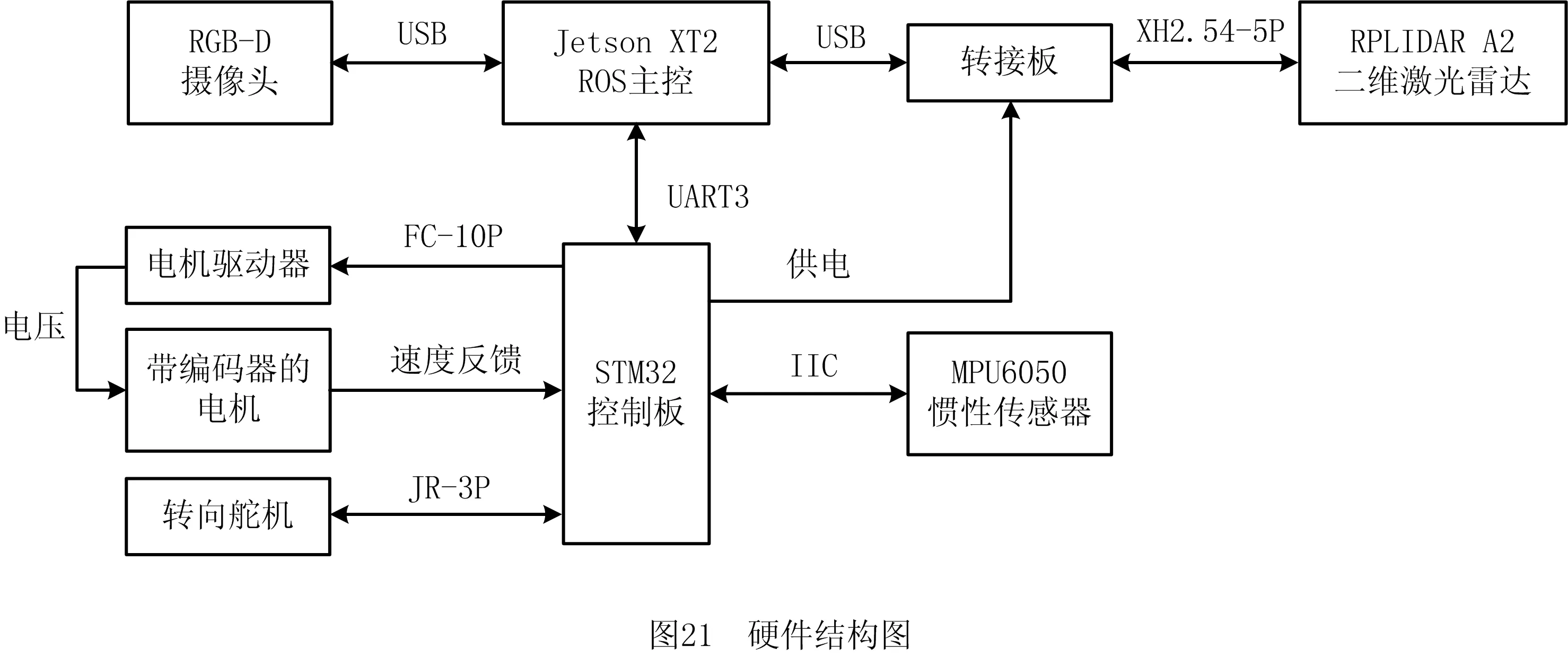
3.2 ROS平台试验
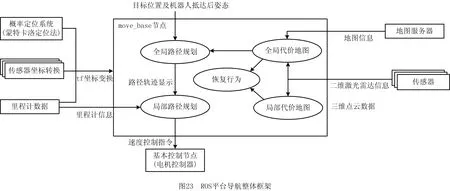

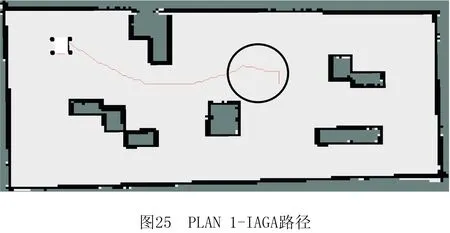

4 结束语
