一类带逻辑脉冲线性系统的最优控制问题

钟荣花, 韦维,2

(1.贵州大学数学与统计学院, 贵州贵阳 550025;2.贵州师范学院数学与大数据学院, 贵州贵阳 550018)

1.引言

在许多事物发展变化的过程中, 常常需要进行观测, 然后根据观测到的情况适时进行干预,使其向良好的方向发展.干预过程在自然界广泛存在, 如人口流动, 渔业养殖与森林管理中的迁移、投放、种植及捕获、采伐等, 这些外界的干扰, 使得系统在短时间内发生较大的变化,由于状态发生本质变化的持续时间相比我们研究的整个过程, 时间显得微乎其微, 因而可认为实质变化过程瞬时完成, 这种现象通常被称为脉冲现象[1–3], 在数学上常用脉冲微分方程（系统）刻画, 这一类系统由于其应用的广泛性, 引起了许多学者的关注[1–3].

脉冲系统的最优控制问题目前已有很多研究成果, 如, 1991年Bressan等[4]通过变分法, 研究了交换向量场上脉冲最优控制的最大值原理并推广到脉冲交换系统; 2006年SHEN等[5]通过Schaefer不动点定理, 考虑了脉冲时滞微分方程解的存在的充分条件; 2011年Dykhta[6]通过Hamilton-Jacobi正则最优性理论的最优性条件, 考虑了Hamilton-Jacobi不等式在一般和脉冲动力系统控制问题中的一些应用; 2020年CHEN[7]利用极小化序列的方法得到了集值映象的存在性定理, 并研究了脉冲微分方程最优控制问题解的存在性和稳定性.

通过对状态的观测判断后再进行干预是生产生活管理中常采取的方式, 本文将研究对给定观测时间进行处置的系统, 这一类系统干预点状态的变化, 通常可以用逻辑表达式进行描述.如鱼塘中鱼苗的投放和鱼的捕获, 可以通过在固定时间点观测池塘中鱼的数量, 决定此时是投放鱼苗还是捕获鱼, 或许什么都不做.此时, 状态的变化可以通过逻辑表达式来刻画.鱼塘中鱼数量的变化可以描述为带逻辑表达式脉冲行为的微分系统, 对控制行为而言, 受控系统是含逻辑判断脉冲的微分系统.系统的运算不仅有代数和微分运算, 还有逻辑运算, 形式更为复杂.

带逻辑判断的线性脉冲系统可描述为

其中A, Bk,Ck为n阶方阵, 状态函数x : [t0,T] →Rn是左连续的分段连续函数, 逻辑函数g : {0,1}n→{0,1}, ∆x(t) = x(t+)−x(t)表示发生的脉冲, x0∈Rn为给定的函数.针对于如上系统的研究, 其困难在于系统中具有代数和微分运算, 还有逻辑运算, 不能用统一的框架处理.对这一类系统的研究不是太多, 2020年周旺旺[8]采用矩阵半张量积这一工具[9], 对上述系统进行了稳定性分析, 并给出了相应的数值仿真.据我们查阅相关文献, 目前我们还未见到关于带逻辑判断脉冲系统最优控制问题的研究成果.因此本文研究带有逻辑判断的脉冲线性微分系统的最优控制问题, 研究内容主要有受控系统解的存在唯一性研究, 最优控制的存在性,最优性条件的推导和应用举例以及模拟仿真几个部分.

2.问题描述

设给定研究区间[t0,T]和观测点0 < t0< t1< ··· < tk< tN= T, k = 1,2,··· ,N −1, 考虑如下线性脉冲受控系统：

3.矩阵半张量积的相关知识

4.受控系统解的存在唯一性

受控系统(2.1)中既有代数和微分运算还有逻辑运算, 为了使用统一的框架处理, 我们需要将脉冲表达式中的逻辑运算通过半张量矩阵的方式, 表示为代数运算, 然后利用一般脉冲微分系统的办法进行处理.

由定理3.1及注3.2可知, 存在唯一的结构矩阵Mk使函数g在tk时刻的值可表示为：

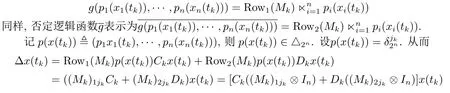
从而将带有逻辑判断的(2.1)式转化为等价的线性脉冲微分系统(4.1).

下面我们讨论系统(4.1)解的存在唯一性.系统(2.1)可转换积分方程

5.最优控制问题解的存在性

为了研究最优控制问题的存在性, 我们假设

(L): 函数Φk(x(·))和L : (t0,T]×Rn×Rm→R为下半连续且有下界的凸函数.控制取值集合U为Rm中的凸紧集.

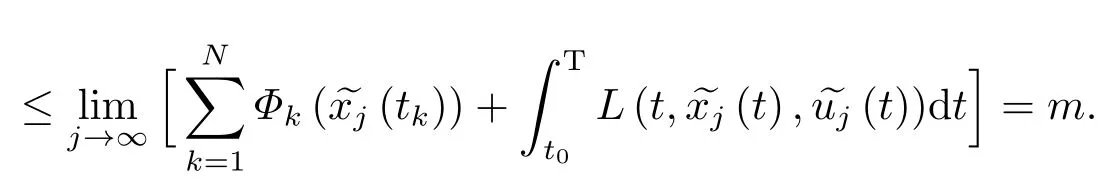
因此u∗(·)是最优解.

6.最优性条件

这一部分, 我们主要研究控制取值集合U为开集或U = Rm的情形下, 最优控制满足的必要条件.

由δu(t)和δx(t) 的任意性, 可得

注6.1在U ⊂Rm开集情形下, 用类似的方法得到相同的最优性条件.

7.应用算例

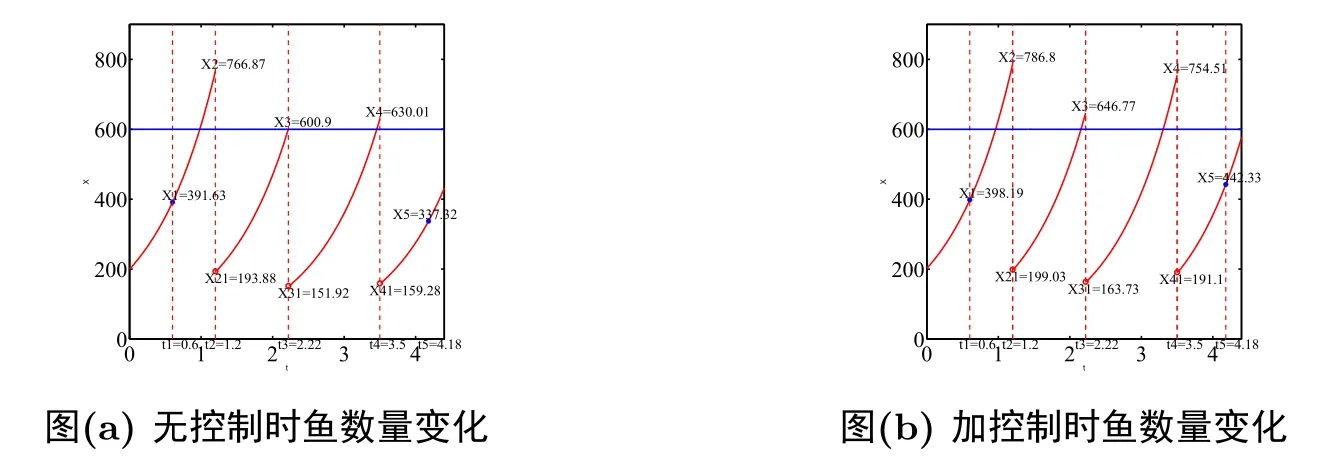
本节我们将给出一个具体例子, 对我们的结论进行说明.以池塘养鱼捕获为例.假设池塘能容纳鱼群的总数为M, 鱼群的增长不受任何因素影响, 在t时刻, x(t)表示池塘里鱼群的总数,r > 0 表示鱼群的内禀增长率, x0表示鱼苗初始投放量, 时刻t = tk表达观测测试时间, 通过逻辑函数g : {0,1} →{0,1}来判断是否需要进行捕获, 如果g = 1, 捕获数量为Ik的鱼群, 反之,若g =0时, 不进行鱼群捕获, 函数g的自变量pk:R →{0,1} 定义为:

其中, u ∈Uad和Uad为容许控制集.观测时间和捕获值与前面相同, 令u(t) = 10t, 利用Matlab计算, 得到加入控制u后池塘中鱼群的变化如图(b).

接下来, 在上述模型的基础上考虑最优控制问题, 给出容许控制集

目标泛函:

其中C为池塘拥有最合适的量, 为给定正常数.

最优控制问题(Q) 寻找u∗∈Uad, 在系统(7.3)的约束下使得J(u)≥J(u∗), ∀u ∈Uad.

和2u∗(t)+λ(t)=0.

从而取M = 900, r = 1.12, x0= 200, C = 5, Tt表示第几个时间段, 总的计算时间Tt都取20, 通过Matlab计算, 利用二阶龙格库塔和复化梯形积分, 得到数值解u(t)和最优J的图像,如图(c).

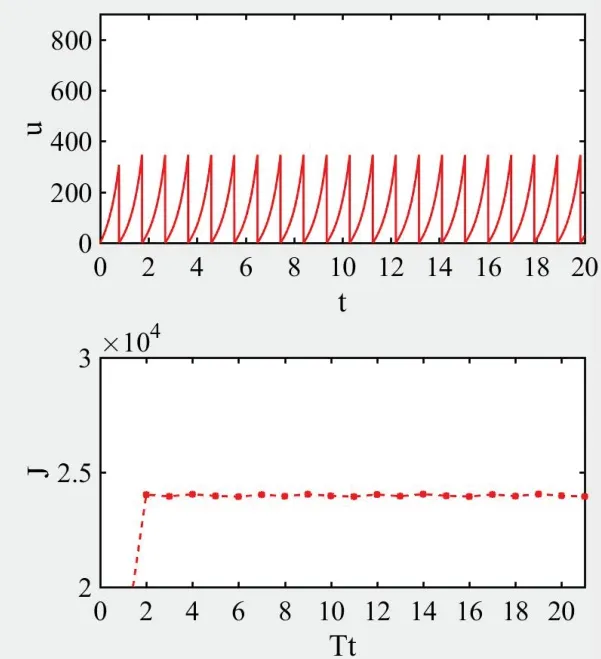
图(c) 最优控制u(t)及最优目标泛函J

8.总结

本文讨论了一类脉冲时刻固定, 且带逻辑判断的线性脉冲系统的最优控制问题, 首先运用矩阵半张量积方法为工具, 把带有逻辑判断的脉冲最优控制问题转换为代数形式的脉冲最优控制问题, 使得问题能够在统一的框架下研究, 在具体的例子下, 可以根据逻辑判断自动选取比较合理的方案; 而且由于考虑的状态方程分段连续, 对于文中的所有问题都是进行分段讨论, 再得到一些相应的结果.通过Banach压缩映像原理, 得到了受控系统解的存在唯一性, 利用Mazur定理, 凸性和下半连续性等证明了最优控制的存在性, 最后, 考虑U = Rm的情形, 推导出最优控制的必要条件, 同时给出了最优控制问题的数值模拟.