具有集群效应和种内竞争的双时滞捕食模型的稳定性与Hopf分支
2022-07-07苏茹燕杨文生
苏茹燕, 杨文生,2,3
(1.福建师范大学数学与统计学院, 福建福州 350117;2.福建省分析数学及应用重点实验室, 福建福州 350117;3.福建省应用数学中心(福建师范大学), 福建福州 350117)
1.引言
Lotka和Volterra提出了经典的Lotka-Volterra捕食模型, 为研究物种之间捕食关系奠定了理论基础.此后众多学者在其基础上进行研究[1−3], 例如文[1]中CHEN等人在其基础上考虑捕食者干扰和扩散因素的影响, 文[2]中Ali Moussaoui等人在其基础上考虑时滞和环境的影响等等.这些模型的功能性反应都是基于假设猎物是独居行为即捕食者可以捕食任何猎物.但众所周知动物大多是群居的, 这就意味着捕食者捕食猎物时会受到猎物集群效应的影响.基于这个事实Ajraldi等人[4]提出了一个更详细的捕食模型, 模型如下:
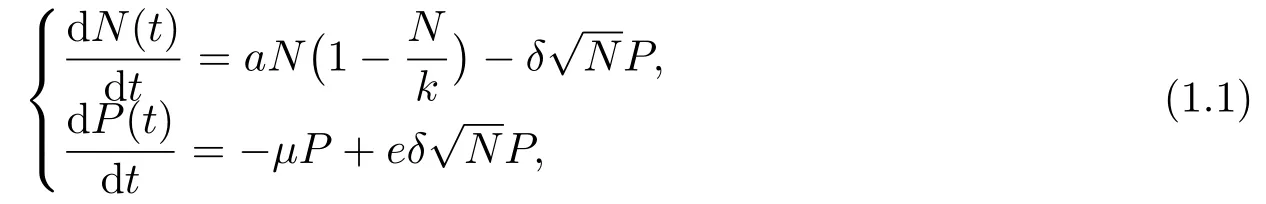
其中N(t)和P(t)分别代表在t时刻猎物和捕食者的密度.a表示内禀增长率, k为环境容纳量, δ表示捕食者种群的捕食率, µ为捕食者种群的自然死亡率, e是捕食者在生物量上的转化率,代表一个捕食者从猎物群边界捕获的猎物数量.在该模型中猎物群体聚集在一起, 捕食者只能捕食猎物群外围的猎物, 他们证明了模型(1.1)极限环的存在性.许多学者在模型(1.1)的基础上考虑了其它因素的影响[5−7], 如考虑食物链情形[5], 猎物会感染疾病的情形[6], 具有时滞情形[7]等.
另一方面, 气候, 环境或猎物数量的变化都可能引起捕食者种群发生种内竞争[8−9].尤其是猎物数量的变化, 当猎物的数量减少时, 会增加捕食者种群的种内竞争.当猎物的数量充裕时, 会减少捕食者种群的种内竞争.根据这一现象, 本文在模型(1.1)的基础上考虑捕食者种内竞争这一因素, 且捕食者的种内竞争系数依赖于猎物数量, 模型如下:
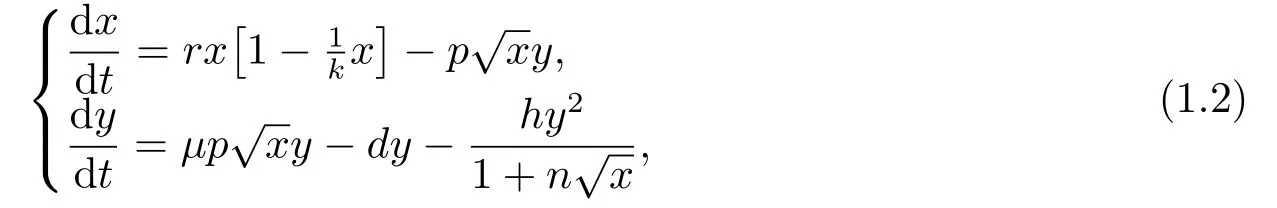
其中x(t)和y(t)分别代表在t时刻猎物和捕食者的密度.r表示内禀增长率, k为环境容纳量, p为捕食者对猎物的捕食率, µ是捕食者在生物量上的转化率, d为捕食者的死亡率, h表示捕食者种群的种内竞争系数, n为捕食者种内竞争依赖于猎物的依赖系数.
考虑到在自然界中大部分动物只有到成年才具备捕食的能力, 且大部分动物在幼年时期都会得到家庭的庇护[10].基于以上考虑, 本文将幼体猎物向成体猎物转化的时间和幼体捕食者向成体捕食者转化的时间列为时滞因素加入模型(1.2), 改进的模型如下:
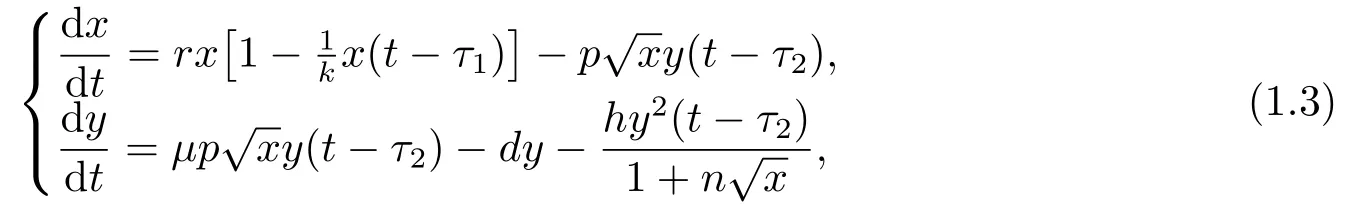
其中τ1表示幼体猎物向成体猎物转化的时滞, τ2表示幼体捕食者向成体捕食者转化的时滞.
在本文的接下来部分, 我们将研究模型(1.3)解的有界性, 平衡点的存在性, 稳定性以及时滞对平衡点稳定性的影响, 最后给出数值模拟验证所得结论的正确性.
2.解的有界性与平衡点的存在性
引理2.1令ω =min{1,d}, Ω =max{x(0),k}, 则紧集

是系统(1.3)的一个正不变集.
证由系统(1.3)的第一个方程可得

计算可知

再由系统(1.3)的第二个方程可得
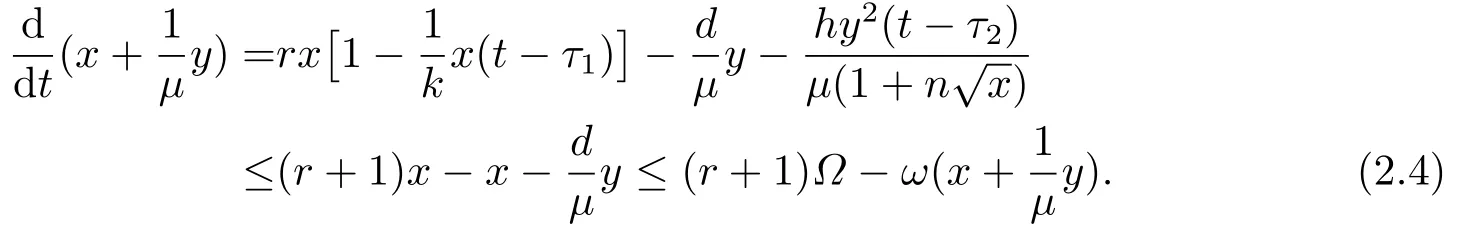
由此可得
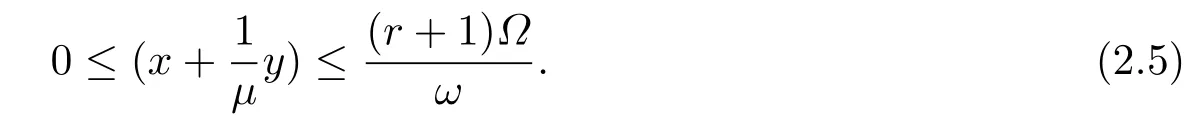
因此可知系统(1.3)的所有解都是有界的, 紧集D是系统(1.3)的一个正不变集.
引理2.2(i)系统(1.3)存在边界平衡点E0=(0,0).
(ii)系统(1.3)存在边界平衡点E1=(k,0).
(iii)系统(1.3)存在唯一的正平衡点E2=(x∗,y∗).
证 (i)显然系统(1.3)存在边界平衡点E0=(0,0);

将系统(1.3)第一个方程乘µ, 与第二个方程相加, 可得到等式

将(2.6)代入(2.7), 整理可得
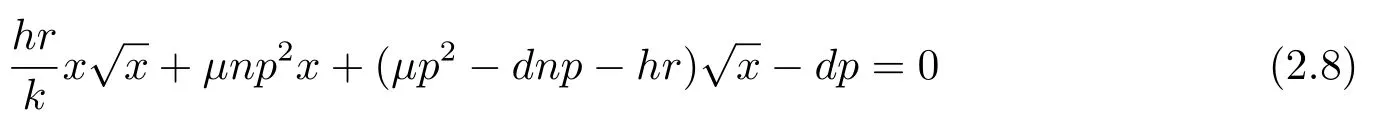

不妨设ξ1, ξ2, ξ3为方程(2.9)的三个实根, 根据根与系数的关系得
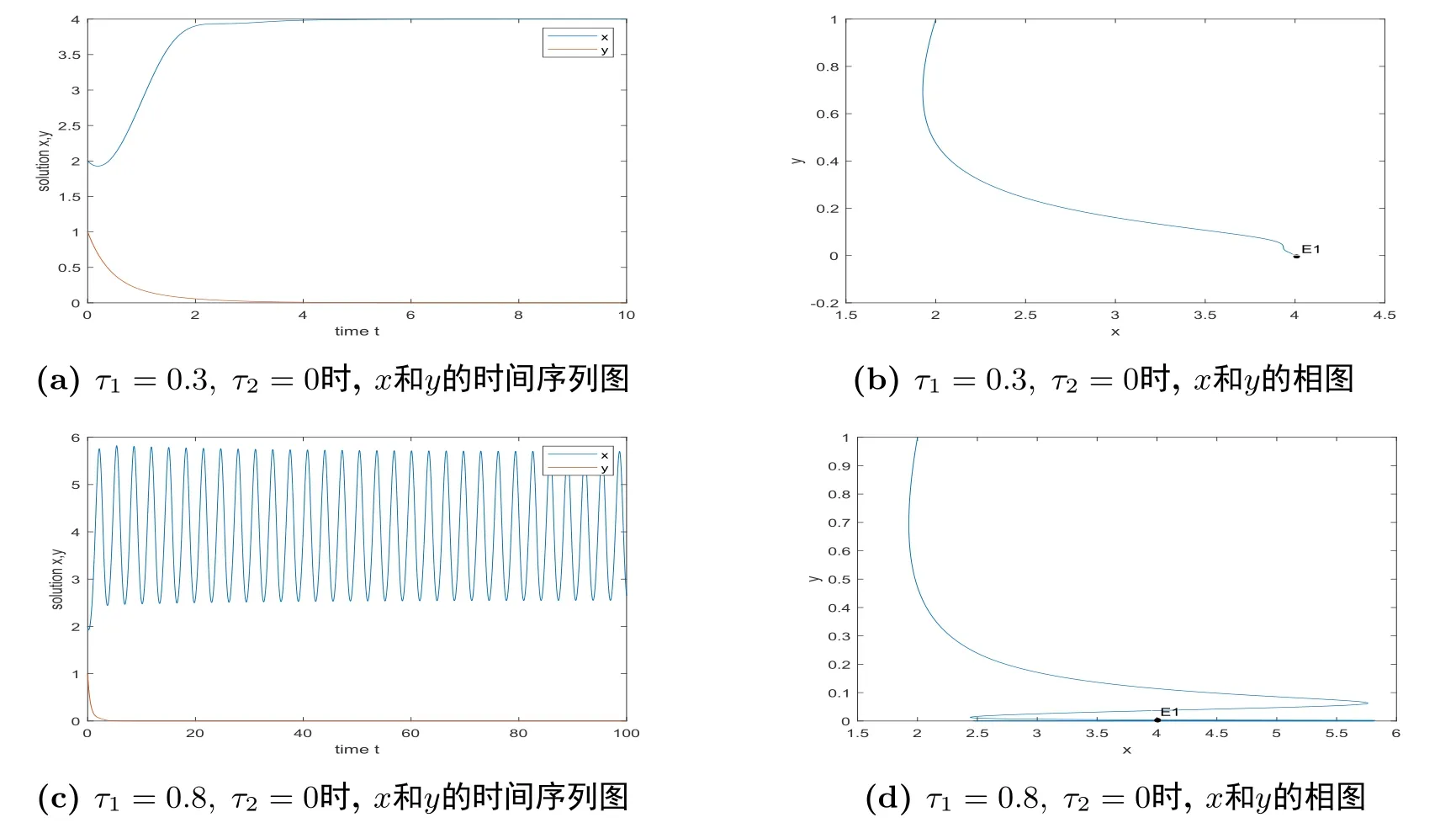
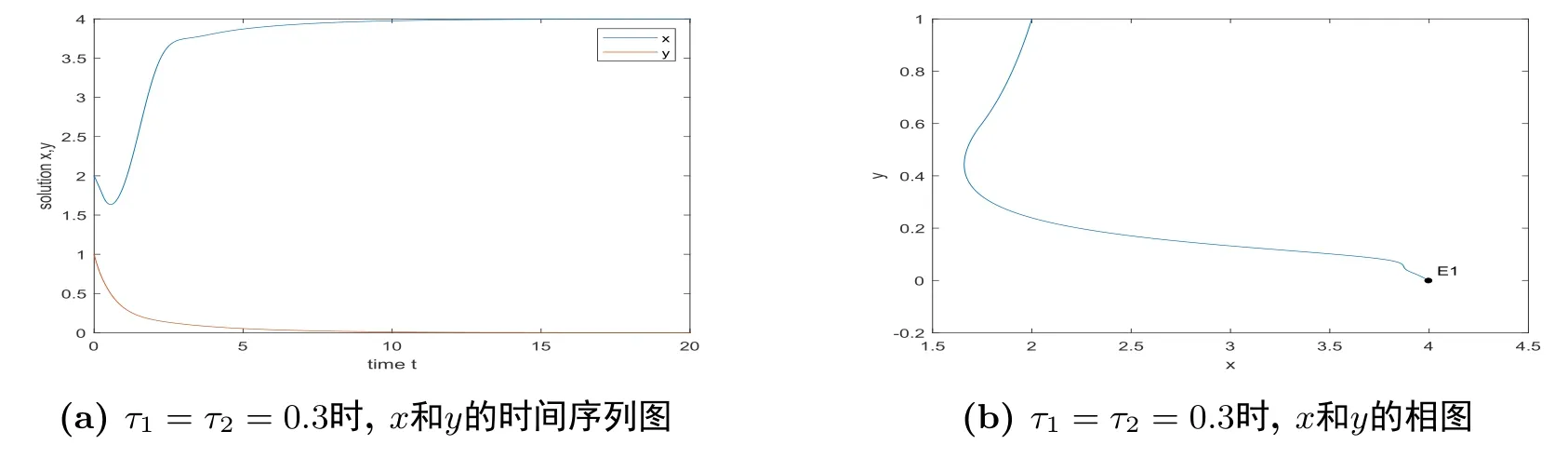
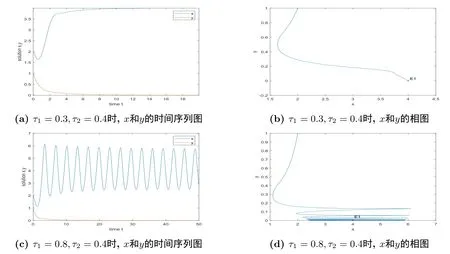
根据(2.10)第一个等式知, 方程(2.9)有负根, 再根据(2.10)第二个等式可推出方程(2.9)的实根为两负一正, 由此可知方程(2.9)有唯一的正根ξ∗, 从而方程(2.8)有唯一的正根x∗= (ξ∗)2.由引理2.1可知, x∗ 本节将分析边界平衡点的稳定性及时滞对边界平衡点稳定性的影响, 并分析局部分支的存在性. 系统(1.3)的Jacobian矩阵为 下面证明系统(1.3)边界平衡点的局部稳定性. 定理3.1在系统(1.3)中, 没有时滞影响时, (i)边界平衡点E0=(0,0)是不稳定的; (ii)当系统(1.3)满足H1a: µp 证(i)由(3.1)知系统(1.3)在E0=(0,0)处的Jacobian矩阵为 显然, 两特征根分别为λ1=r, λ2=−d, 有一个特征根是正根, 因此E0=(0,0)是不稳定的. (ii)由(3.1)知系统(1.3)在E1=(k,0)处的Jacobian矩阵为 两特征根分别为λ1= −r < 0, λ2= µp−d, 由假设条件H1a得λ2< 0, 因此E1= (k,0)是局部渐近稳定的. 下面分析在没有时滞影响下, 系统(1.3)可能存在的分支. 定理3.2当参数满足系统(1.3)在E1处发生跨临界分支, 其中d为分支参数. 从而 由上式可知, V 和W满足 由Sotomayor定理可知, 系统(1.3)在E1处发生跨临界分支.证毕. 接下来分析时滞对边界平衡点E1稳定性的影响. 由(3.1)知, 当时滞存在时, 系统(1.3)在E1=(k,0)处的Jacobian矩阵为 对应的特征方程为 其中a1=d, b1=r, b2=rd, c1=− 下面分析当τ1, τ2处于以下几个可能的情况时, 对边界平衡点E1稳定性的影响. 情况1 τ1>0, τ2=0.根据(3.10)可知, 此时特征方程为 讨论特征方程(3.11)纯虚根的存在性, 令λ=zi(z >0)为特征方程(3.11)的解, 代入得 将实部和虚部分离可得 整理可得 再令ζ =z2, 代入(3.14)得 整理得 由(3.13)可知 因此 其中p1=a1+b1,p2=b2,q1=c1,q2=d1. 接下来讨论特征方程(3.26)纯虚根的存在性, 令λ=zi(z >0)为特征方程(3.26)的解, 代入方程(3.26), 将实部和虚部分离可得 整理可得 再令ζ =z2, 代入(3.28)得 由韦达定理可知, 当H1a满足时方程(3.29)没有正根.由上述讨论, 可得到以下定理: 定理3.4当τ1= 0且H1a:< d满足时, 对任意的τ2> 0, 边界平衡点E1都是局部渐近稳定的. 情况3 τ1=τ2=τ.根据(3.10)可知, 此时特征方程为 其中q01=b1+c1, q02=b2.两边同乘eλτ得 接下来讨论特征方程(3.32)纯虚根的存在性, 令λ=zi(z >0)为特征方程(3.32)的解, 代入得 分离实部和虚部, 有 其中Q1(z) = d1−z2, Q2(z) = a1z, Q3(z) = −q02, Q4(z) = d1−z2, Q5(z) = a1z, Q6(z) =−q01z. 由(3.34)可得 其中Q00(z) = Q1(z)Q4(z) + Q2(z)Q5(z), Q01(z) = Q3(z)Q4(z) + Q2(z)Q6(z), Q02(z) =Q1(z)Q6(z)−Q3(z)Q5(z).由(3.35)可得 假设H1c:(3.36)有一个正根z0.则(3.32)有一对纯虚根±iz0.与z0所对应的时滞τ的临界值为 (i)若τ ∈[0,τ0), 则边界平衡点E1是局部渐近稳定的; (ii)若τ =τ0, 系统(1.3)在E1处产生Hopf分支. 情况4 τ1> 0, τ2> 0.考虑特征方程(3.10)中τ2处于稳定区间, τ1被视为参数.讨论特征方程(3.10)纯虚根的存在性, 令λ=zi(z >0)为特征方程(3.10)的解, 分离实部和虚部得 其中M1=b1z−d1sin zτ2, M2=b2+d1cos zτ2, M3=z2−c1z sin zτ2, M4=−a1z−c1z cos zτ2. 根据(3.40)有 假设H1e:方程(3.41)至少有有限个正根.不妨用z1,z2,··· ,zk表示其正根.每个zi, i=1,2,··· ,k相对应的时滞临界值为 其中 本节将分析正平衡点的稳定性及时滞对正平衡点稳定性的影响, 并分析局部分支的存在性. 对应的特征方程为 接下来分析时滞对正平衡点E2稳定性的影响. 由(3.1)知, 当时滞存在时, 系统(1.3)在E2处的Jacobian矩阵为 对应的特征方程为 其中 下面分析当τ1, τ2处于以下几个可能的情况时, 对正平衡点E2稳定性的影响. 情况1 τ1>0, τ2=0.根据(4.4)可知, 此时特征方程为 接下来讨论特征方程(4.5)纯虚根的存在性, 令λ=zi(z >0)为特征方程的解, 代入得 实部和虚部分离得 整理可得 令ζ =z2得 其中 若以下两个条件其中之一满足时, 可知方程(4.9)至少存在一个正根. 接下来讨论特征方程(4.18)纯虚根的存在性, 令λ = zi(z > 0)为特征方程的解, 代入方程(4.18), 分离实部和虚部得 整理可得 两边同乘eλτ得 接下来讨论特征方程(4.29)纯虚根的存在性, 令λ=zi(z >0)为特征方程的解, 代入得 分离实部和虚部得 假设H2m:(4.33)有一个正根z0.则(4.29)有一对纯虚根±iz0.对于z0所对应的时滞τ的临界值为 本节将通过数值模拟验证前面得到的结论, 下面先验证关于边界平衡点E1的相关结论. 对于τ1= τ2= 0的情形, 取r = 2, k = 4, p = 2, µ = 0.5, d = 3, h = 1, n = 1, 初始条件为:(x(0),y(0))= (2,1).可得d >= 2即系统(1.3)满足H1a, 则存在全局吸引的点E1=(4,0)即捕食者种群灭绝, 猎物种群存活, 如图1. 图1 r = 2, k = 4, p = 2, µ = 0.5, d = 3, h = 1, n = 1, τ1 = τ2 = 0 初始条件分别为:(x(0),y(0))=(2,1) 对于τ1= 0, τ2> 0的情形, 取r = 2, k =4, p =2, µ =0.5, d = 3, h = 1, n =1, 初始条件为:(x(0),y(0))=(0.8,0.6), 满足H1a.图3描绘了当τ2分别取3和6时, 对平衡点E1的影响, 其中实线表示τ1= 0, τ2= 0, 虚线表示τ1= 0, τ2= 3, 点线表示τ1=0, τ2=6.从图3可以看出,τ2增加会延迟物种到达平衡点的时间, 且τ2的改变对x物种的影响比对y物种的影响大. 图3 r =2, k =4, p=2, µ=0.5, d=3, h=1, n=1 初始条件分别为:x(0),y(0)=(0.8,0.6) 图2 r =2, k =4, p=2, µ=0.5, d=3, h=1, n=1, 初始条件分别为:(x(0),y(0))=(2,1) 对于τ1= τ2= τ的情形, 取r = 2, k = 4, p = 2, µ = 0.5, d = 2.5, h = 1, n = 1, 初始条件为:(x(0),y(0))= (2,1).满足H1a, H1c, 通过计算可得U1U3+U2U4= 890, 满足H1d, 此时τ0= 0.7854.如图4(a)-(d)所示, 当τ = 0.3 < τ0时, 平衡点E1= (2,0) 是局部渐近稳定的.当τ =0.8>τ0时, 平衡点E1=(4,0)是不稳定的, 产生周期解. 图4 r =2, k =4, p=2, µ=0.5, d=2.5, h=1, n=1, 初始条件分别为:(x(0),y(0))=(2,1) 对于τ1> 0, τ2> 0的情形, 取r = 2, k = 4, p = 2, µ = 0.5, d = 2.5, h = 1, n = 1, τ2=0.4 初始条件为:(x(0),y(0))=(2,1).满足H1a, H1e, 通过计算可得N1N3+N2N4=52.08710, 满足H1f, 此时= 0.7854.如图5(a)-(d)所示, 当τ1= 0.3 <时, 平衡点E1= (4,0)是局部渐近稳定的.当τ1=0.8>时, 平衡点E1=(4,0) 是不稳定的, 产生周期解. 图5 r =2, k =4, p=2, µ=0.5, d=2.5, h=1, n=1, 初始条件分别为:(x(0),y(0))=(2,1) 下面验证关于正平衡点E2的相关结论. 图6 r = 2, k = 4, p = 2, µ = 0.5, d = 1, h = 1, n = 1, τ1 = τ2 = 0 初始条件分别为:(x(0),y(0))=(0.8,0.6) 图7 r = 2, k = 4, p = 2, µ = 0.5, d = 1, h = 1, n = 1, 初始条件分别为:(x(0),y(0))= (2,1) 图8 r =2, k =4, p=2, µ=0.5, d=1, h=1, n=1, 初始条件分别为:x(0),y(0)=(0.8,0.6) 图10 r =2, k =4, p=2, µ=0.5, d=1, h=1, n=1, 初始条件分别为:x(0),y(0)=(0.8,0.6) 本文同时考虑了猎物种群集群效应和捕食者种群种内竞争这两个因素, 研究了一类捕食者和猎物具有生长时滞捕食模型的平衡点稳定性.首先讨论无捕食者边界平衡点的稳定性, 发现在没有时滞影响下, 当< d时, 无捕食者边界平衡点是局部渐近稳定的.当= d时, 无捕食者边界平衡点处发生跨临界分支.其次分析了时滞引起的边界平衡点附近周期解的存在性, 结果表明在有时滞影响下, 当幼体猎物向成体猎物转化的时滞τ1为零的情况下, 幼体捕食者向成体捕食者转化的时滞τ2不会影响无捕食者边界平衡点的稳定性,且τ2增加会延迟物种数量到达平衡点的时间, τ2的改变对猎物数量的影响比对捕食者数量的影响大, 这意味着当猎物生长时滞为零时, 捕食者生长时滞只会延缓捕食者灭绝的时间, 不会影响它走向灭绝.其他情况下的τ1, τ2会影响无捕食者边界平衡点的稳定性, 当时滞超过阈值时无捕食者边界平衡点不稳定, 进而存在周期解, 这表明, 如果时滞较短, 捕食者和猎物种群的数量最终将都处于固定的水平, 随着时滞的增加, 猎物的数量以周期的方式振荡变化.接着给出了保证正平衡点局部渐近稳定的充分条件.最后分析了时滞引起的正平衡点处Hopf分支的存在性, 结果表明时滞τ1, τ2会影响正平衡点的稳定性, 当时滞超过阈值时正平衡点不稳定, 且经历Hopf分支.从生物学的角度来看, 这结果表明, 如果时滞较短, 捕食者和猎物种群的数量最终都将处于固定的水平, 随着时滞的增加, 物种数量以周期的方式变化, 即捕食者和猎物将以周期振荡的方式共存.3.边界平衡点的稳定性分析和局部分支分析
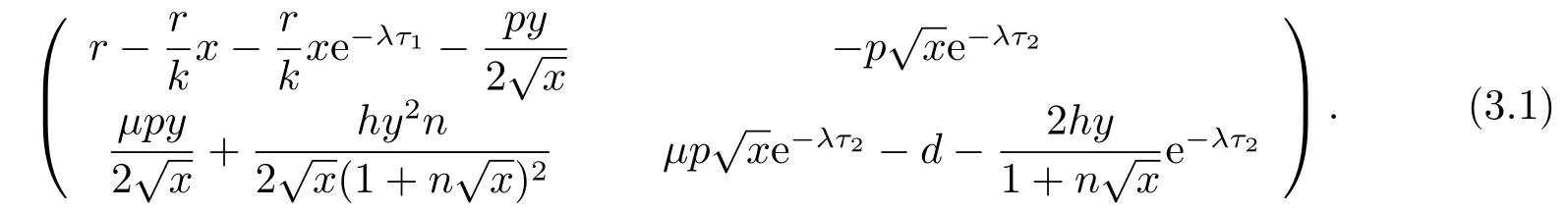



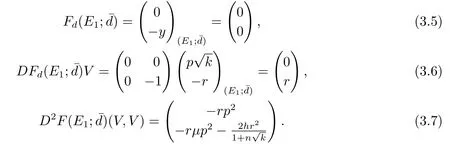
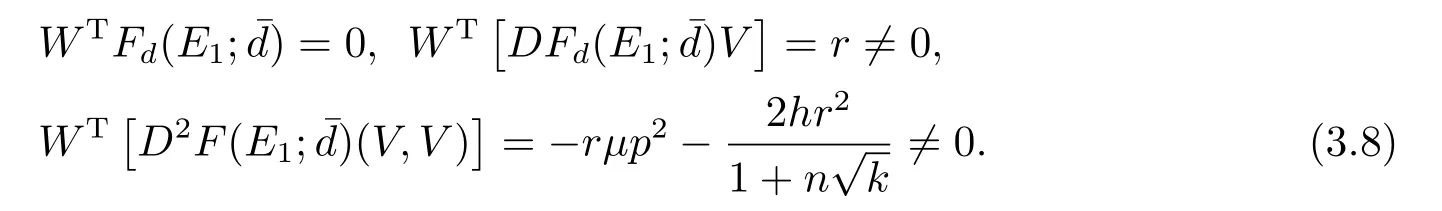

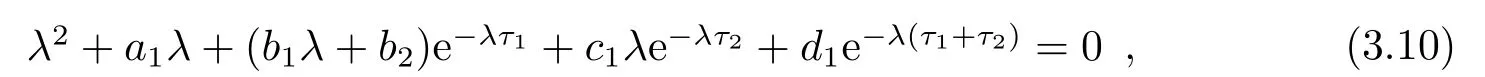

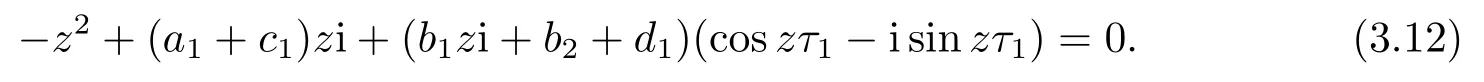

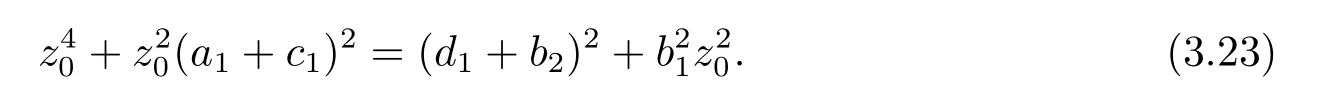



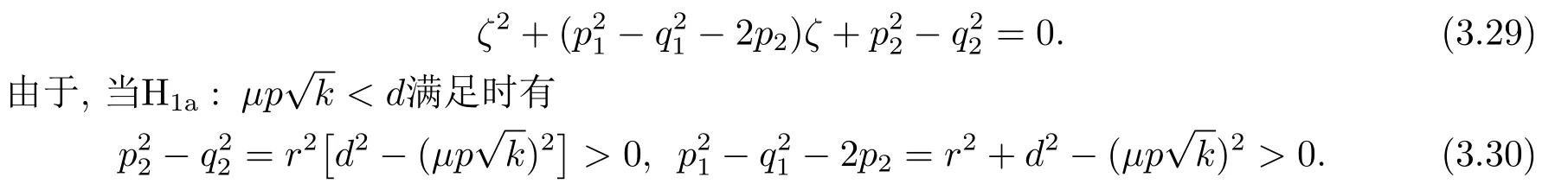
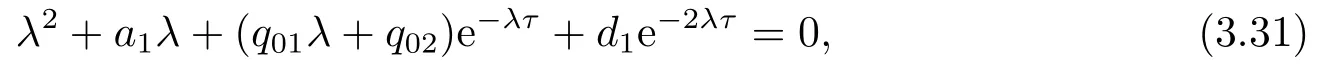
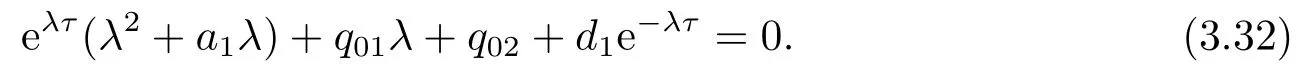
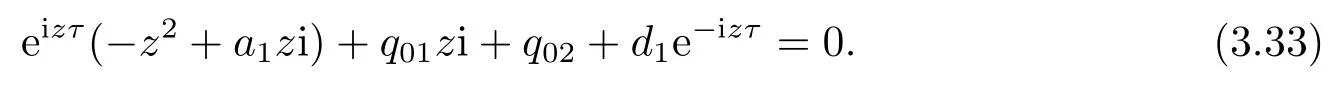





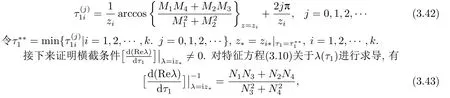

4.正平衡点的稳定性分析和局部分支分析


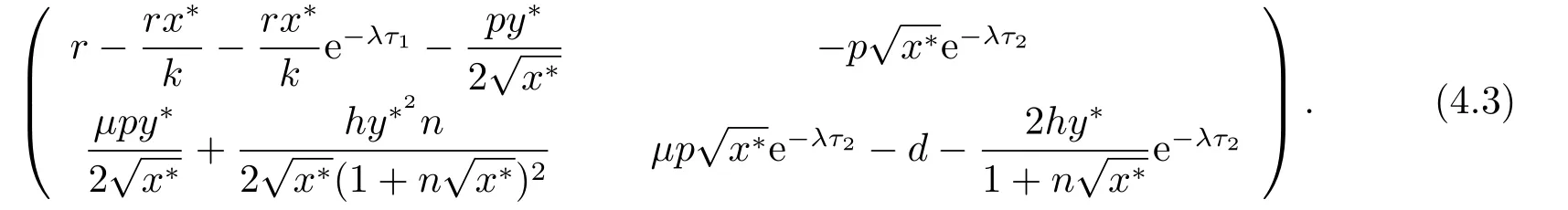
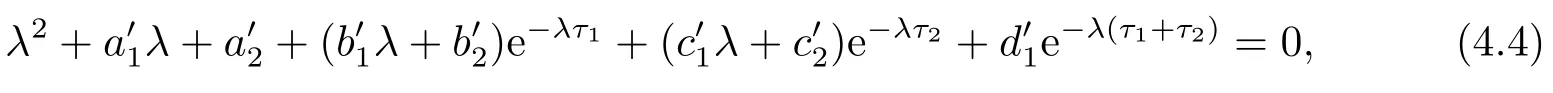
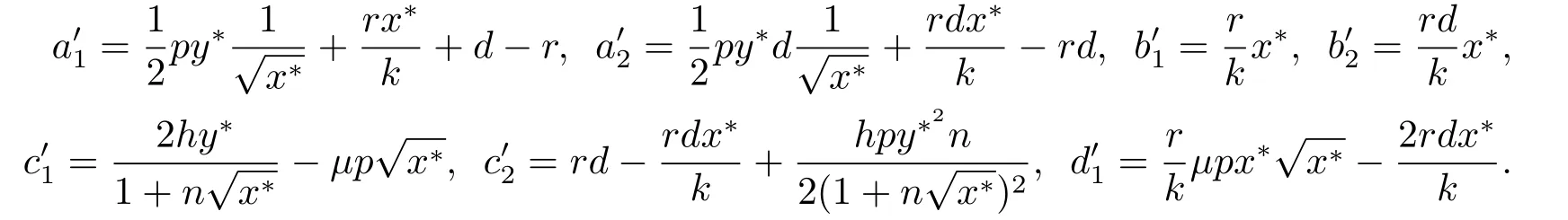
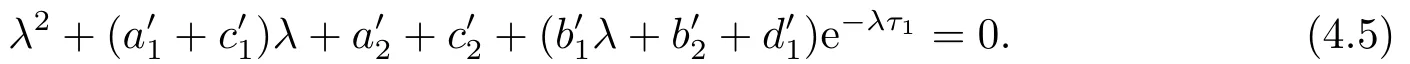
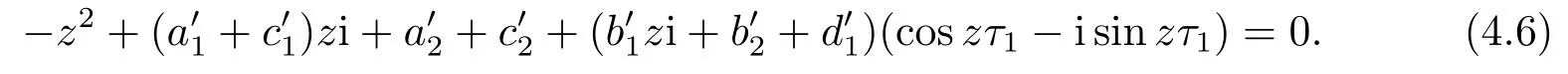
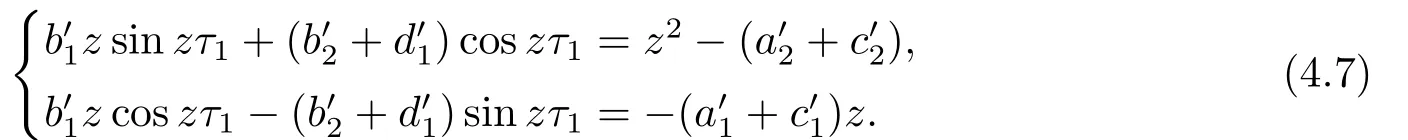
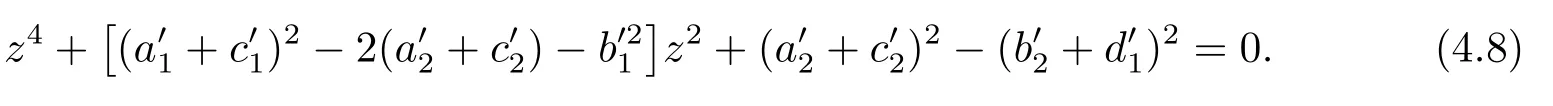
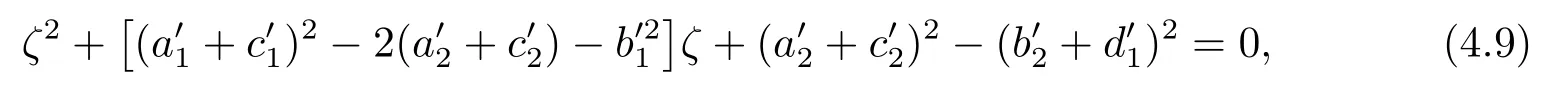





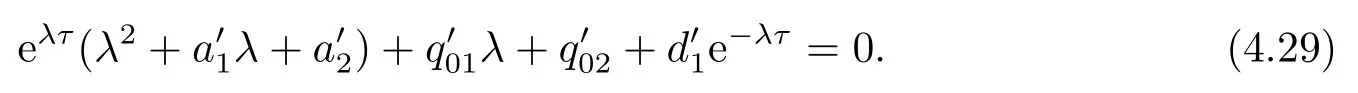
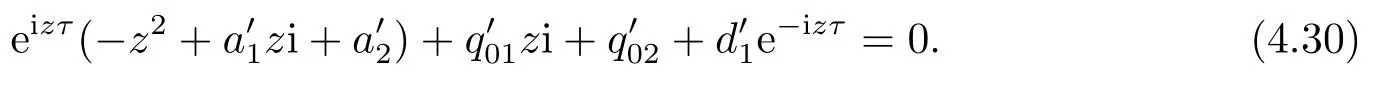
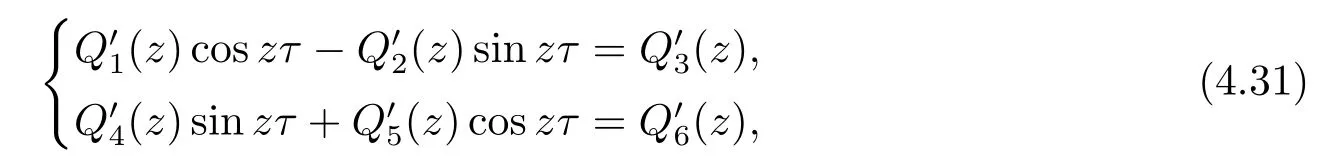
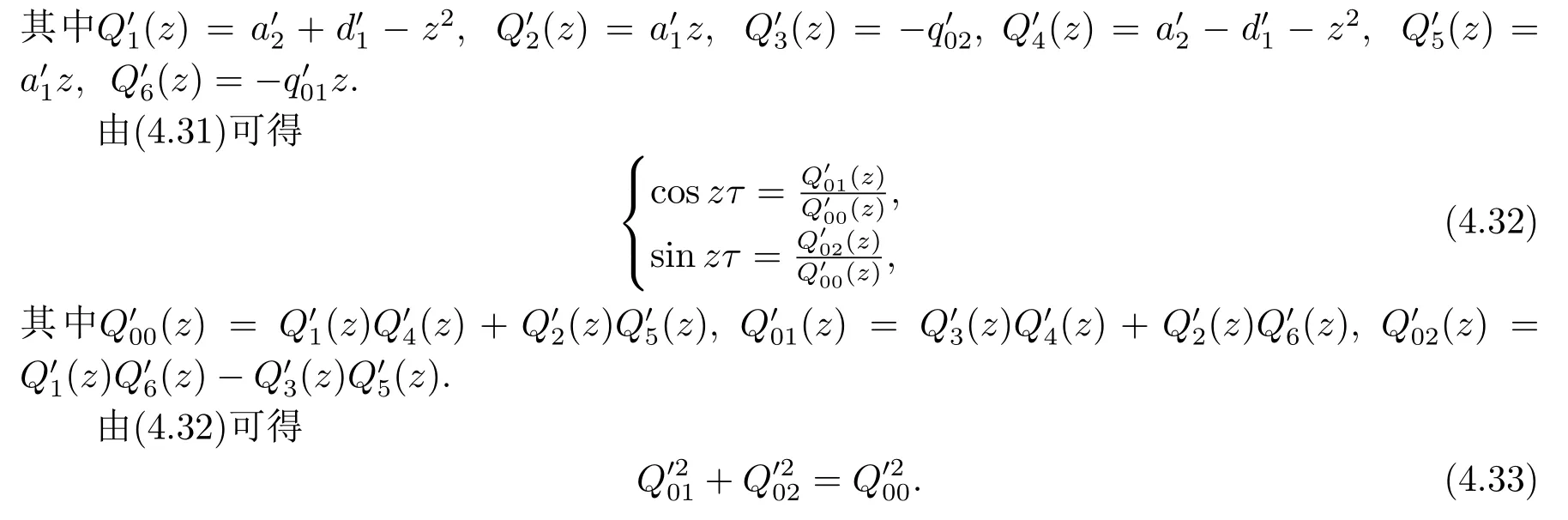


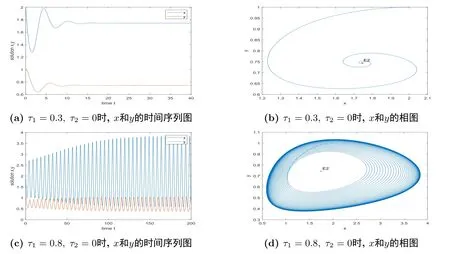
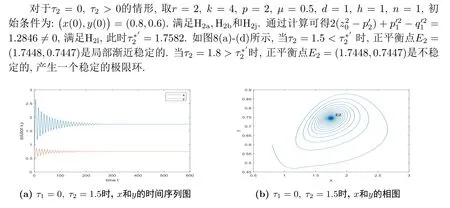
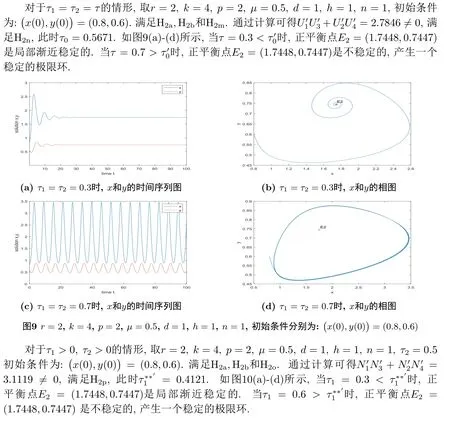
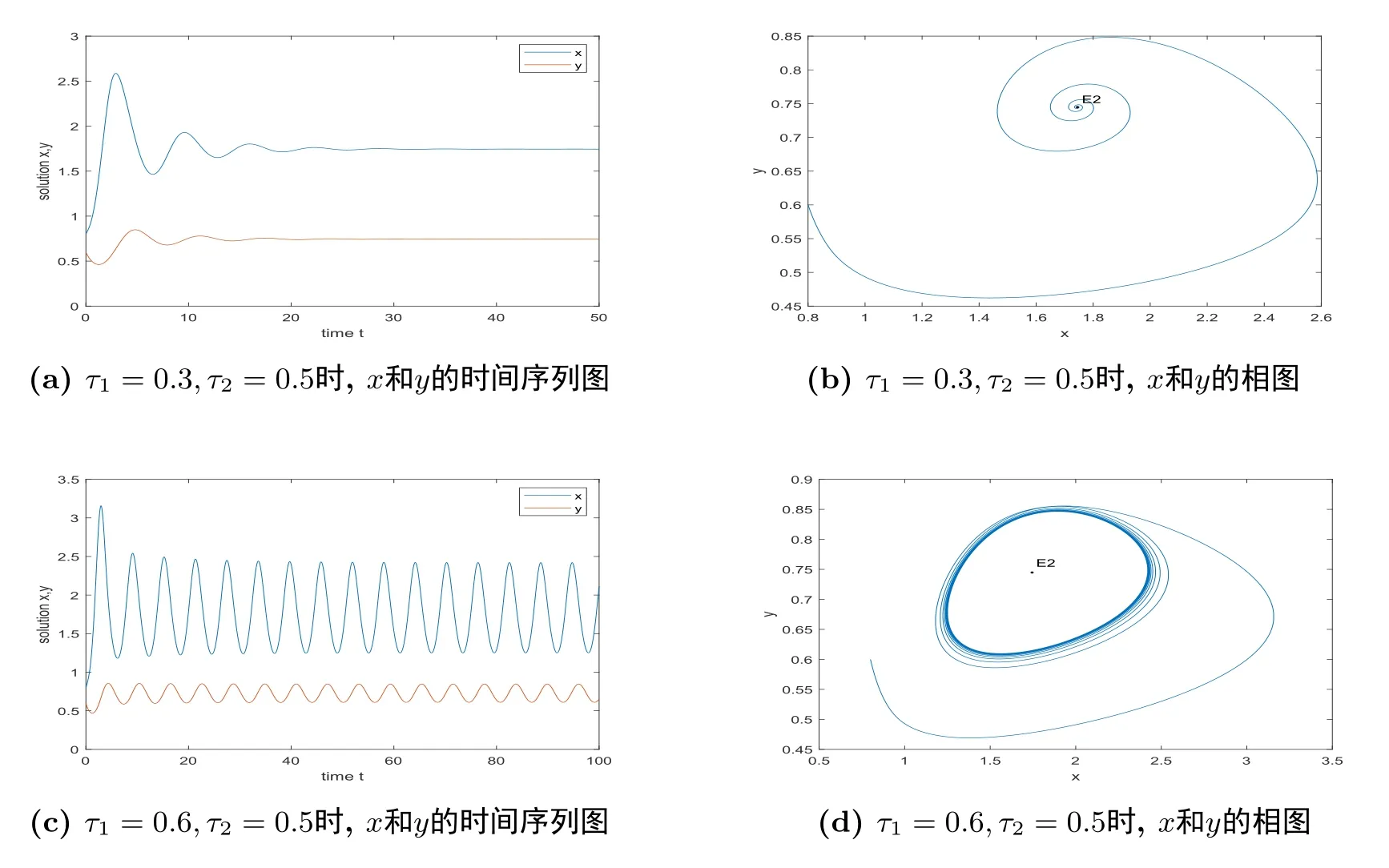
5.数值模拟







6.结论
